16.6 Titrations and Neutralization Calculations

Learning Objectives

By the end of this section, you will be able to:

  • Explain the use of acid-base indicators in determining pH of a solution and outline how it is used in a titration experiment
  • Know the steps of an acid-base titration experiment
  • Perform neutralization calculations involving strong acids and strong bases

In the previous section, neutralization reactions were introduced. This section will examine the basics of acid-base titrations and perform neutralization calculations between strong acids and strong bases.

Titrations

When hydrochloric acid is reacted with sodium hydroxide, an acid/base mole ratio of 1:1 is required for full neutralization.

HCl(aq) + NaOH(aq) → NaCl(aq) + H2O(l)

If instead the hydrochloric acid were reacted with barium hydroxide, the mole ratio would be 2:1.

2 HCl(aq) + Ba(OH)2(aq) → BaCl2(aq) + 2 H2O(l)

Two moles of HCl are required to completely neutralize one mole of Ba(OH)2. In a balanced neutralization equation, the moles of H+ ions supplied by the acid will be equal to the moles of OH− ions supplied by the base. The equivalence point is the point in a neutralization reaction when the number of moles of hydrogen ions is equal to the number of moles of hydroxide ions.

In the laboratory, you may need to determine the concentration of an acid or a base whose concentration is not known. This can be accomplished by performing a controlled neutralization reaction. A titration is an experiment in which a solution, whose concentration is known, is gradually added to a measured volume of another solution in order to determine its concentration. Typically, the titrant (the known solution) is added from a buret to a known volume of the analyte (the unknown concentration). Many titrations are acid-base neutralization reactions, although other types of titrations can also be performed.

In order to perform an acid-base titration, the chemist must have a way to visually detect that the neutralization reaction has reached the equivalence point. An indicator is a substance that has a distinctly different colour when in an acidic or basic solution. A commonly used indicator for strong acid-strong base titrations is phenolphthalein. Solutions in which a few drops of phenolphthalein have been added, turn from colourless to brilliant pink as the solution turns from acidic to basic (Figure 16.6a).

Four test tubes are shown containing solutions at various pH all contain the pH indicator, phenolphthalein. From left to right: Test tube 1 is an orange colour since the solution is at a pH less than zero. Test tube 2 is a clear solution and information indicates it will remain clear for any solution ranging from pH of zero to 8.3. Test tube 3 is pink and information indicates it will be a pink colour for any solution ranging from pH 8.3 through 10. Finally test tube 4 is a clear solution, and information indicates it will remain clear for any solution that has a pH greater than 10. They provide ranges of pH. Exact pH ranges of this indicator are provided by the supplier when purchased used in lab.
Figure 16.6a: Phenolphthalein at different pH values: Four test tubes are shown containing solutions at various pH, all containing the pH indicator, phenolphthalein. From left to right: At a pH less than zero, phenolphthalein will turn orange, as shown in the first test tube on the left. At a pH between 0 and 8.3, the solution will remain clear. A solution between a pH of zero to 8.3 through 10, the solution will be pink. Finally a solution with this indicator will be clear for any solutions with a pH greater than 10. Exact pH ranges of this indicator are provided by the supplier when purchased used in lab (credit: modification of work by Siegert, PD / pH ranges corrected by Jackie MacDonald).

The steps in a titration reaction are outlined below.

  1. A measured volume of an acidic solution (the analyte) whose concentration is unknown is added to an Erlenmeyer flask.
  2. Several drops of an indicator are added to the acid and mixed by swirling the flask.
  3. A buret is filled with a basic solution (the titrant) of known molarity.
  4. The stopcock of the buret is opened and base is slowly added to the acid while the flask is constantly swirled to ensure mixing. The stopcock is closed at the exact point at which the indicator just changes colour. If the colour change does not remain after swirling, the neutralization reaction has not yet reached completion.

The standard solution is the solution in a titration whose concentration is known. In the titration described above, the base solution is the standard solution. It is very important in a titration to add the solution from the buret slowly so that the point at which the indicator changes colour can be found accurately. The end point of a titration is the point at which the indicator changes colour. When phenolphthalein is the indicator, the end point will be signified by a faint pink colour.

Watch Setting Up and Performing a Titration (6min 52sec).

Video Source: Carolina Biological (2010, February 17). Setting up and performing a titration. [Video]. YouTube.

Other pH indicators behave in essentially the same way.

Watch What Are Indicators & How Do We Use Them? | Chemical Tests | Chemistry | FuseSchool (3min 18s).

Video Source: FuseSchool – Global Education. (2013, June 3). What are indicators & how do we use them? | Chemical tests | Chemistry [Video]. YouTube.

Neutralization Calculations

As shown at the beginning of this section, when hydrochloric acid is reacted with sodium hydroxide, an acid/base mole ratio of 1:1 is required for full neutralization as shown in the balance chemical equation below:

HCl(aq) + NaOH(aq) → NaCl(aq) + H2O(l)

However, as we have learned, not all acids and bases neutralize at a one to one mole ratio. When a strong diprotic or triprotic acid or base is used in a titration neutralization reaction, the mole ratio needs to be taken into consideration when performing calculations. Let’s reexamine the neutralization of hydrochloric acid with diprotic barium hydroxide:

2 HCl(aq) + Ba(OH)2(aq) → BaCl2(aq) + 2 H2O(l)

Two moles of HCl are required to completely neutralize one mole of Ba(OH)2. The strong acid, HCl, furnishes 1 H+ ion; whereas, Ba(OH)2  ionizes 2 OH– ions. In a balanced neutralization equation, the moles of H+ ions supplied by the acid is equal to the moles of OH− ions supplied by the base. The equivalence point is the point in a neutralization reaction when the number of moles of hydrogen ions is equal to the number of moles of hydroxide ions.

Therefore, it is of utmost importance that students consider mole ratios of the acid and base in their calculations when performing neutralization calculations.

There are different ways to solve neutralization problems: solving neutralization problems using stoichiometry will be outlined in this section.

Performing Stoichiometric Calculations to Solve Neutralization Problems

Take a closer look at Figure 16.6b, which is a modified version of Figure 9.2a from 9.2 – Mole-Mass and Mass-Mass Calculations. Focus your attention on the four rectangles inside the red coloured outline. These provide a flowchart on the steps needed to solve a neutralization reaction problem.

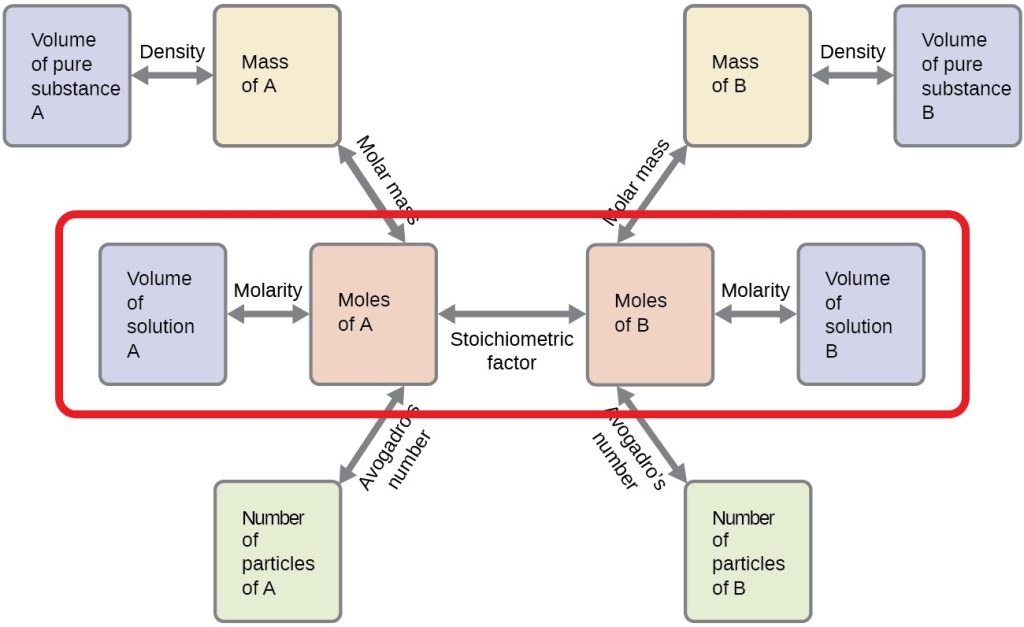
This flowchart shows 4 horizontally aligned rectangles connected by double headed arrows. To the left, a rectangle is shaded lavender and is labeled, “Volume of solution A.” This rectangle is followed by a horizontal double headed arrow labeled, “Molarity”. It connects to a second rectangle which is shaded pink and is labeled “Moles of A”. This rectangle is followed by a horizontal double headed arrow labeled, “Stoichiometric factor”. It connects to a third pink coloured rectangle and is labeled “Moles of B”. Finally, this rectangle is followed by a horizontal double headed arrow labeled, “Molarity” and it connects to the fourth rectangle that is coloured lavender which is labeled “Volume of B”.
Figure 16.6b: Stoichiometry Flowchart for Neutralization Calculations. (Image Source: General Chemistry 1 & 2, CC BY 4.0). (credit: Chemistry (OpenStax), CC BY 4.0).

Calculating the Unknown Molarity of an Acid/Base in a Neutralization Reaction:

Follow the steps below to solve for an unknown molarity.

  • Take known volume of known solution “A” and multiply it by molarity of solution A to calculate the moles of A.
  • Next, apply the mole ratio calculation to determine the moles of solution B.
  • Finally, apply the final stoichiometric calculation using the moles of solution B and given volume of solution B to calculate the molarity of solution B needed to neutralize solution A.

Example 16.6a

In a titration of hydrochloric acid with barium hydroxide, 32.00 mL of 0.150 M HCl is required to neutralize 26.75 mL of the barium hydroxide solution. Calculate the molarity of the barium hydroxide solution. (Remember, you must work in litres for volume since you are performing mole calculations using units of molarity, which are moles/L).

Solution

Step 1: List the known values, write the balanced chemical equation, and and plan the problem.

Known

  • molarity of the HCl solution = 0.150 M
  • volume of the HCl solution = 32.00 mL = 0.03200L
  • volume of the Ba(OH)2 solution = 26.75 mL = 0.02675L
  • Balanced Chemical Equation: 2HCl(aq) + Ba(OH)2(aq) → BaCl2(aq) + 2H2O(l)
  • Mole ratio of acid to base in balanced chemical equation is 2:1

Unknown

  • molarity of the Ba(OH)2 solution = ?

Step 2 : Determine the moles of HCl that were consumed in the reaction. 

  • mol HCl = M × L = 0.150M × 0.03200L = 0.00480 mols of HCl

Step 3: From the mole ratio, calculate the moles of Ba(OH)2 that reacted.

  • mol Ba(OH)2 = 0.00480 mols HCl x [1 mol Ba(OH)2 / 2 mol HCl] = 0.00240 mols = 2.40 x 10-3 mols of Ba(OH)2 

Step 4: Determine the molarity of Ba(OH)2 by dividing the moles by the volume.

  • [Ba(OH)2] = 2.40 x 10-3 mols / 0.02675 L = 0.0897 M 

Therefore the molarity of the basic barium hydroxide solution needed to neutralize the acid solution is 0.0897 M or 8.97 x 10-2 M.

Source: “Example 16.6a” by Jackie MacDonald, licensed under CC BY-NC 4.0

Example 16.6b

Suppose that a titration is performed between a strong acid and strong base: 20.70 mL of 0.500 M NaOH is required to reach the end point when titrated against 15.00 mL of HBr of unknown concentration. Use the neutralization equation to determine the concentration of hydrobromic acid used in this titration.

Solution

Step 1: List the known values, write the balanced chemical equation, and and plan the problem.

Known

  • molarity of the NaOH solution = 0.500 M
  • volume of the NaOH solution = 20.70 mL
  • volume of the HBr solution = 15.00 mL
  • Balanced Chemical Equation: HBr(aq) + NaOH(aq) → NaBr(aq) + H2O(l)
  • Mole ratio of acid to base in balanced chemical equation is 1:1.

Unknown

  • molarity of the HBr solution = ?

Step 2 : Determine the moles of HBr that were consumed in the reaction.

  • mol NaOH = M × L = 0.500M × 20.70L = 0.01035 mols of NaOH

Step 3: From the mole ratio, calculate the moles of HBr that reacted.

  • mol HBr = 0.01035 mols NaOH x [1 mol HBr / 1 mol NaOH] = 0.01035 mols HBr = 1.035 x 10-2 mols HBr

Step 4: Determine the molarity of HBr by dividing the moles by the volume.

  • [HBr] = 1.035 x 10-2 mols / 0.015 L = 0.690M HBr

Therefore the molarity of the Hydrobromic acid solution needed to neutralize the base solution is 0.690M.

Source: “Example 16.6b” by Jackie MacDonald, licensed under CC BY-NC 4.0

Exercise 16.6a

35.00 mL of 0.125 M HCl is required to neutralize 25.00 mL of KOH. Determine the concentration of the base solution.

Check Your Answer[1]

Exercise 16.6b

15.75 mL of 0.350M H2SO4 is required to neutralize 10.00 mL of NaOH. Determine the concentration of the sodium hydroxide solution.

Check Your Answer[2]

Source: “Exercise 16.6b” by Jackie MacDonald is licensed under CC BY-NC 4.0.

Calculating the Unknown Volume of an Acid/Base in a Neutralization Reaction:

If you are asked to solve for an unknown volume of an acid or base in a neutralization reaction problem, follow these steps:

  • Take known volume of known solution “A” and multiply it by molarity of solution A to calculate the moles of A.
  • Next, apply the mole ratio calculation to determine the moles of solution B.
  • Finally, apply the final stoichiometric calculation using the moles of solution B and given molarity of solution B to calculate the volume of solution B needed to neutralize solution A.

Example 16.6c

What volume, in mL, of a 0.139 M solution of barium hydroxide is required to neutralize 45.00 mL of 0.256 M HCl?

Solution

Step 1: List the known values, write the balanced chemical equation, and plan the problem.

Known

  • molarity of the HCl solution = 0.256 M
  • volume of the HCl solution = 45.00 mL = 0.04500 L
  • molarity of the Ba(OH)2 solution = 0.139 M
  • Balanced Chemical Equation: 2HCl(aq) + Ba(OH)2(aq) → BaCl2(aq) + 2H2O(l)
  • Mole ratio of acid to base in balanced chemical equation is 2:1.

Unknown

  • volume of the Ba(OH)2 solution = ?

Step 2 : Determine the moles of HCl that were consumed in the reaction. 

  • mol HCl = M × L = 0.256 M × 0.04500 L = 0.01152 mols of HCl

Step 3: From the mole ratio, calculate the moles of Ba(OH)2 that reacted.

  • mol Ba(OH)2 = 0.01152 mols HCl x [1 mol Ba(OH)2 / 2 mol HCl] = 0.00576 mols = 5.76 x 10-3 mols of Ba(OH)2 

Step 4: Determine the volume of Ba(OH)2 using moles and molarity of Ba(OH)2.

  • [Ba(OH)2] = 5.76 x 10-3 mols x 1 L / 0.139 mols = 0.0414 L

Final Step: Convert volume to mL

  • 0.0414 L x 1000 mL/ 1L = 41.4 mL

Therefore 41.4 mL of the barium hydroxide solution is needed to neutralize 45.00 mL of 0.256 M HCl.

Source: “Example 16.6c” by Jackie MacDonald, licensed under CC BY-NC 4.0

Exercise 16.6c

What volume, in mL, of a 0.500 M solution of sodium hydroxide would be required to neutralize 40.0 mL of a 0.375 M H2SO4 solution?

Check Your Answer[3]

Source: “Exercise 16.6c” by Jackie MacDonald, licensed under CC BY-NC 4.0

Attribution & References

Except where otherwise noted, this page is adapted by Jackie MacDonald from “21.4 Acid-Base Neutralization” In CK-12 Chemistry – Intermediate by CK-12, licensed under CK-12 Curriculum Materials license.

  1. 0.175 M KOH ↵
  2. 0.276 M NaOH ↵
  3. Step 1: List the known values, write the balanced chemical equation, and plan the problem. Known
    • molarity of the H2SO4 solution = 0.375 M
    • volume of the H2SO4 solution = 40.0 mL = 0.0400 L
    • molarity of the NaOH solution = 0.500 M
    • Balanced Chemical Equation: H2SO4(aq) + 2NaOH(aq) → Na2SO4(aq) + 2H2O(l)
    • Mole ratio of acid to base in balanced chemical equation is 1:2.
    Unknown
    • volume of the H2SO4 solution = ?
    Step 2 : Determine the moles of H2SO4 that were consumed in the reaction. 
    • mol H2SO4 = M × L = 0.375 M × 0.0400 L = 0.0150 mols of H2SO4
    Step 3: From the mole ratio, calculate the moles of NaOH that reacted.
    • mol NaOH = 0.0150 mols H2SO4 x [2 mol NaOH / 1 mol H2SO4 ] = 0.0300 mols = 3.00 x 10-2 mols of NaOH
    Step 4: Determine the volume of NaOH using moles and molarity of NaOH.
    • [NaOH] = 3.00 x 10-2 mols x 1 L / 0.500 mols = 0.0600 L
    Final Step: Convert volume to mL
    • 0.0600 L x 1000 mL/ 1L = 60.0 mL
    Therefore 60.0 mL of the sodium hydroxide solution is needed to neutralize 40.0 mL of a 0.375 M H2SO4 solution. ↵
definition

License

Icon for the Creative Commons Attribution 4.0 International License

Enhanced Introductory College Chemistry Copyright © 2023 by Gregory Anderson; Caryn Fahey; Jackie MacDonald; Adrienne Richards; Samantha Sullivan Sauer; J.R. van Haarlem; and David Wegman is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book