13.3 Phase Transitions
Learning Objectives
- Define phase transitions and phase transition temperatures
- Explain the relation between phase transition temperatures, intermolecular attractive forces, and kinetic energy
- Describe the processes represented by typical heating and cooling curves, and compute heat flows and enthalpy changes accompanying these processes

We witness and utilize changes of physical state, or phase transitions, in a great number of ways. As one example of global significance, consider the evaporation, condensation, freezing, and melting of water. These changes of state are essential aspects of our earth’s water cycle as well as many other natural phenomena and technological processes of central importance to our lives. In this module, the essential aspects of phase transitions are explored.
Vaporization and Condensation
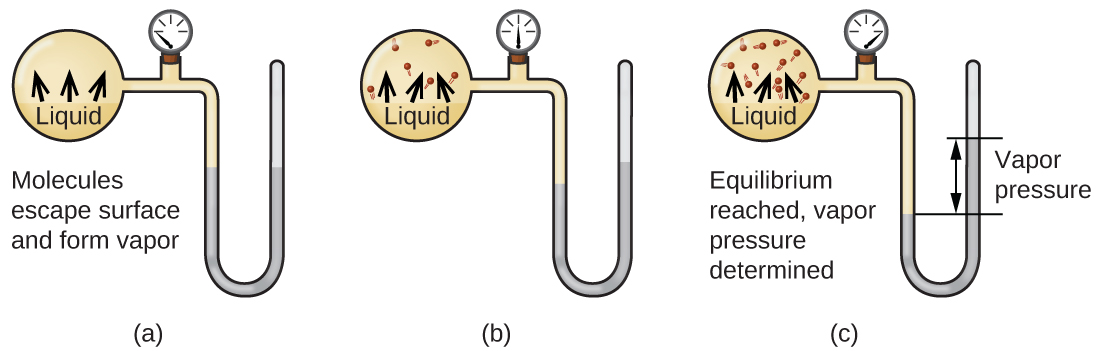
When a liquid vaporizes in a closed container, gas molecules cannot escape. As these gas phase molecules move randomly about, they will occasionally collide with the surface of the condensed phase, and in some cases, these collisions will result in the molecules re-entering the condensed phase. Figure 13.3a shows a simple phase change diagram. The change from the gas phase to the liquid is called condensation. When the rate of condensation becomes equal to the rate of vaporization, neither the amount of the liquid nor the amount of the vapour in the container changes. The vapour in the container is then said to be in equilibrium with the liquid. Keep in mind that this is not a static situation, as molecules are continually exchanged between the condensed and gaseous phases. Such is an example of a dynamic equilibrium, the status of a system in which reciprocal processes (for example, vaporization and condensation) occur at equal rates. The pressure exerted by the vapour in equilibrium with a liquid in a closed container at a given temperature is called the liquid’s vapour pressure (or equilibrium vapour pressure). The area of the surface of the liquid in contact with a vapour and the size of the vessel have no effect on the vapour pressure, although they do affect the time required for the equilibrium to be reached. We can measure the vapour pressure of a liquid by placing a sample in a closed container, like that illustrated in Figure 13.3b, and using a manometer to measure the increase in pressure that is due to the vapour in equilibrium with the condensed phase.
The chemical identities of the molecules in a liquid determine the types (and strengths) of intermolecular attractions possible; consequently, different substances will exhibit different equilibrium vapour pressures. Relatively strong intermolecular attractive forces will serve to impede vaporization as well as favouring “recapture” of gas-phase molecules when they collide with the liquid surface, resulting in a relatively low vapour pressure. Weak intermolecular attractions present less of a barrier to vaporization, and a reduced likelihood of gas recapture, yielding relatively high vapour pressures. The following example illustrates this dependence of vapour pressure on intermolecular attractive forces.
Example 13.3a
Explaining Vapour Pressure in Terms of IMFs
Given the shown structural formulas for these four compounds, explain their relative vapour pressures in terms of types and extents of IMFs:

Solution
Diethyl ether has a very small dipole and most of its intermolecular attractions are London forces. Although this molecule is the largest of the four under consideration, its IMFs are the weakest and, as a result, its molecules most readily escape from the liquid. It also has the highest vapour pressure. Due to its smaller size, ethanol exhibits weaker dispersion forces than diethyl ether. However, ethanol is capable of hydrogen bonding and, therefore, exhibits stronger overall IMFs, which means that fewer molecules escape from the liquid at any given temperature, and so ethanol has a lower vapour pressure than diethyl ether. Water is much smaller than either of the previous substances and exhibits weaker dispersion forces, but its extensive hydrogen bonding provides stronger intermolecular attractions, fewer molecules escaping the liquid, and a lower vapour pressure than for either diethyl ether or ethanol. Ethylene glycol has two −OH groups, so, like water, it exhibits extensive hydrogen bonding. It is much larger than water and thus experiences larger London forces. Its overall IMFs are the largest of these four substances, which means its vaporization rate will be the slowest and, consequently, its vapour pressure the lowest.
Exercise 13.3a
At 20 °C, the vapour pressures of several alcohols are given in this table. Explain these vapour pressures in terms of types and extents of IMFs for these alcohols:
| Compound | methanol CH3OH | ethanol C2H5OH | propanol C3H7OH | butanol C4H9OH |
|---|---|---|---|---|
| Vapour Pressure at 20 °C | 11.9 kPa | 5.95 kPa | 2.67 kPa | 0.56 kPa |
Check Your Answer[1]
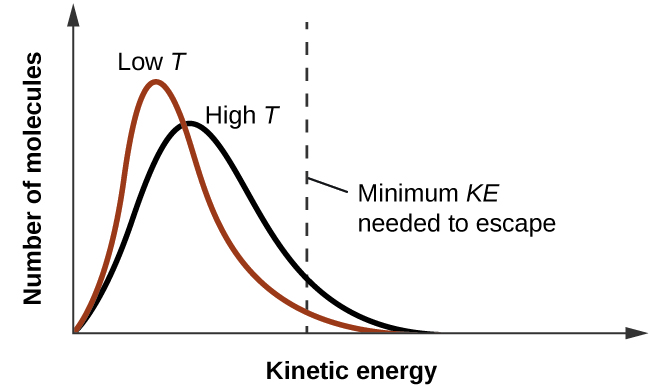
As temperature increases, the vapour pressure of a liquid also increases due to the increased average KE of its molecules. Recall that at any given temperature, the molecules of a substance experience a range of kinetic energies, with a certain fraction of molecules having a sufficient energy to overcome IMF and escape the liquid (vaporize). At a higher temperature, a greater fraction of molecules have enough energy to escape from the liquid, as shown in Figure 13.3c. The escape of more molecules per unit of time and the greater average speed of the molecules that escape both contribute to the higher vapour pressure.
Boiling Points
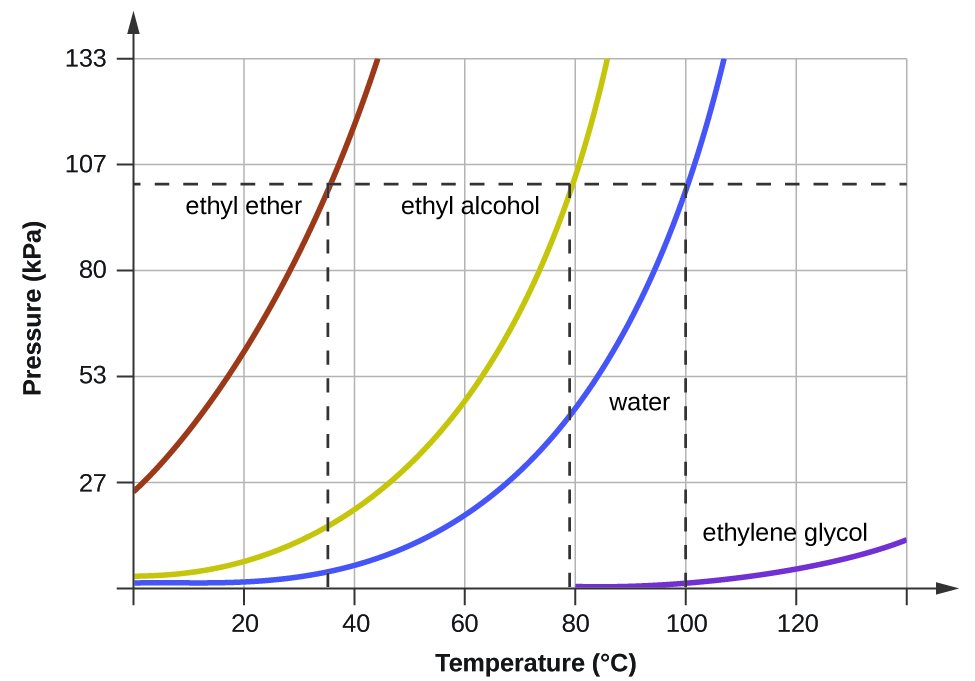
When the vapour pressure increases enough to equal the external atmospheric pressure, the liquid reaches its boiling point. The boiling point of a liquid is the temperature at which its equilibrium vapour pressure is equal to the pressure exerted on the liquid by its gaseous surroundings. For liquids in open containers, this pressure is that due to the earth’s atmosphere. The normal boiling point of a liquid is defined as its boiling point when surrounding pressure is equal to 1 atm (101.3 kPa). Figure 13.3d shows the variation in vapour pressure with temperature for several different substances. Considering the definition of boiling point, these curves may be seen as depicting the dependence of a liquid’s boiling point on surrounding pressure.
Example 13.3b
A Boiling Point at Reduced Pressure
A typical atmospheric pressure in Leadville, Colorado (elevation 10,200 feet) is 68 kPa. Use the graph in Figure 13.3d to determine the boiling point of water at this elevation.
Solution
The graph of the vapour pressure of water versus temperature in Figure 13.3d indicates that the vapour pressure of water is 68 kPa at about 90 °C. Thus, at about 90 °C, the vapour pressure of water will equal the atmospheric pressure in Leadville, and water will boil.
Exercise 13.3b
Check Your Learning Exercise (Text Version)
The boiling point of ethyl ether was measured to be 10 °C at a base camp on the slopes of Mount Everest. Use Figure 13.3d to determine the approximate atmospheric pressure at the camp.
- 40 kPa
- 41 kPa
- 39 kPa
- 51kPa
Check Your Answer[2]
Source: “Exercise 13.3b” is adapted from “Example 10.3-2” in General Chemistry 1 & 2, a derivative of Chemistry (Open Stax) by Paul Flowers, Klaus Theopold, Richard Langley & William R. Robinson, licensed under CC BY 4.0.
The quantitative relation between a substance’s vapour pressure and its temperature is described by the Clausius-Clapeyron equation:
where ΔHvap is the enthalpy of vaporization for the liquid, R is the gas constant, and ln A is a constant whose value depends on the chemical identity of the substance. This equation is often rearranged into logarithmic form to yield the linear equation:
This linear equation may be expressed in a two-point format that is convenient for use in various computations, as demonstrated in the example exercises that follow. If at temperature T1, the vapour pressure is P1, and at temperature T2, the vapour pressure is T2, the corresponding linear equations are:
Since the constant, ln A, is the same, these two equations may be rearranged to isolate ln A and then set them equal to one another:
which can be combined into:
Example 13.3c
Estimating Enthalpy of Vaporization
Isooctane (2,2,4-trimethylpentane) has an octane rating of 100. It is used as one of the standards for the octane-rating system for gasoline. At 34.0 °C, the vapour pressure of isooctane is 10.0 kPa, and at 98.8 °C, its vapour pressure is 100.0 kPa. Use this information to estimate the enthalpy of vaporization for isooctane.
Solution
The enthalpy of vaporization, ΔHvap, can be determined by using the Clausius-Clapeyron equation:
Since we have two vapour pressure-temperature values (T1 = 34.0 °C = 307.2 K, P1 = 10.0 kPa and T2 = 98.8 °C = 372.0 K, P2 = 100 kPa), we can substitute them into this equation and solve for ΔHvap. Rearranging the Clausius-Clapeyron equation and solving for ΔHvap yields:
Note that the pressure can be in any units, so long as they agree for both P values, but the temperature must be in kelvin for the Clausius-Clapeyron equation to be valid.
Exercise 13.3c
At 20.0 °C, the vapour pressure of ethanol is 5.95 kPa, and at 63.5 °C, its vapour pressure is 53.3 kPa. Use this information to estimate the enthalpy of vaporization for ethanol.
Check Your Answer[3]
Example 13.3d
Estimating Temperature (or Vapour Pressure)
For benzene (C6H6), the normal boiling point is 80.1 °C and the enthalpy of vaporization is 30.8 kJ/mol. What is the boiling point of benzene in Denver, where atmospheric pressure = 83.4 kPa?
Solution
If the temperature and vapour pressure are known at one point, along with the enthalpy of vaporization, ΔHvap, then the temperature that corresponds to a different vapour pressure (or the vapour pressure that corresponds to a different temperature) can be determined by using the Clausius-Clapeyron equation:
Since the normal boiling point is the temperature at which the vapour pressure equals atmospheric pressure at sea level, we know one vapour pressure-temperature value (T1 = 80.1 °C = 353.3 K, P1 = 101.3 kPa, ΔHvap = 30.8 kJ/mol) and want to find the temperature (T2) that corresponds to vapour pressure P2 = 83.4 kPa. We can substitute these values into the Clausius-Clapeyron equation and then solve for T2. Rearranging the Clausius-Clapeyron equation and solving for T2 yields:
Exercise 13.3d
For acetone (CH3)2CO, the normal boiling point is 56.5 °C and the enthalpy of vaporization is 31.3 kJ/mol. What is the vapour pressure of acetone at 25.0 °C?
Check Your Answer[4]
Enthalpy of Vaporization
Vaporization is an endothermic process. The cooling effect can be evident when you leave a swimming pool or a shower. When the water on your skin evaporates, it removes heat from your skin and causes you to feel cold. The energy change associated with the vaporization process is the enthalpy of vaporization, ΔHvap. For example, the vaporization of water at standard temperature is represented by:
As described in the chapter on thermochemistry, the reverse of an endothermic process is exothermic. And so, the condensation of a gas releases heat:
Example 13.3e
Using Enthalpy of Vaporization
One way our body is cooled is by evaporation of the water in sweat (Figure 13.3e). In very hot climates, we can lose as much as 1.5 L of sweat per day. Although sweat is not pure water, we can get an approximate value of the amount of heat removed by evaporation by assuming that it is. How much heat is required to evaporate 1.5 L of water (1.5 kg) at T = 37 °C (normal body temperature); ΔHvap = 43.46 kJ/mol at 37 °C.

Solution
We start with the known volume of sweat (approximated as just water) and use the given information to convert to the amount of heat needed:
Thus, 3600 kJ of heat are removed by the evaporation of 1.5 L of water.
Exercise 13.3e
How much heat is required to evaporate 100.0 g of liquid ammonia, NH3, at its boiling point if its enthalpy of vaporization is 4.8 kJ/mol?
Check Your Answer[5]
Melting and Freezing
When we heat a crystalline solid, we increase the average energy of its atoms, molecules, or ions and the solid gets hotter. At some point, the added energy becomes large enough to partially overcome the forces holding the molecules or ions of the solid in their fixed positions, and the solid begins the process of transitioning to the liquid state or melting. At this point, the temperature of the solid stops rising, despite the continual input of heat, and it remains constant until all of the solid is melted. Only after all of the solid has melted will continued heating increase the temperature of the liquid (Figure 13.3f).

If we stop heating during melting and place the mixture of solid and liquid in a perfectly insulated container so no heat can enter or escape, the solid and liquid phases remain in equilibrium. This is almost the situation with a mixture of ice and water in a very good thermos bottle; almost no heat gets in or out, and the mixture of solid ice and liquid water remains for hours. In a mixture of solid and liquid at equilibrium, the reciprocal processes of melting and freezing occur at equal rates, and the quantities of solid and liquid therefore remain constant. The temperature at which the solid and liquid phases of a given substance are in equilibrium is called the melting point of the solid or the freezing point of the liquid. Use of one term or the other is normally dictated by the direction of the phase transition being considered, for example, solid to liquid (melting) or liquid to solid (freezing).
The enthalpy of fusion and the melting point of a crystalline solid depend on the strength of the attractive forces between the units present in the crystal. Molecules with weak attractive forces form crystals with low melting points. Crystals consisting of particles with stronger attractive forces melt at higher temperatures.
The amount of heat required to change one mole of a substance from the solid state to the liquid state is the enthalpy of fusion, ΔHfus of the substance. The enthalpy of fusion of ice is 6.0 kJ/mol at 0 °C. Fusion (melting) is an endothermic process:
The reciprocal process, freezing, is an exothermic process whose enthalpy change is −6.0 kJ/mol at 0 °C:
Sublimation and Deposition
Some solids can transition directly into the gaseous state, bypassing the liquid state, via a process known as sublimation. At room temperature and standard pressure, a piece of dry ice (solid CO2) sublimes, appearing to gradually disappear without ever forming any liquid. Snow and ice sublime at temperatures below the melting point of water, a slow process that may be accelerated by winds and the reduced atmospheric pressures at high altitudes. When solid iodine is warmed, the solid sublimes and a vivid purple vapour forms (Figure 13.3g). The reverse of sublimation is called deposition, a process in which gaseous substances condense directly into the solid state, bypassing the liquid state. The formation of frost is an example of deposition.

Like vaporization, the process of sublimation requires an input of energy to overcome intermolecular attractions. The enthalpy of sublimation, ΔHsub, is the energy required to convert one mole of a substance from the solid to the gaseous state. For example, the sublimation of carbon dioxide is represented by:
Likewise, the enthalpy change for the reverse process of deposition is equal in magnitude but opposite in sign to that for sublimation:
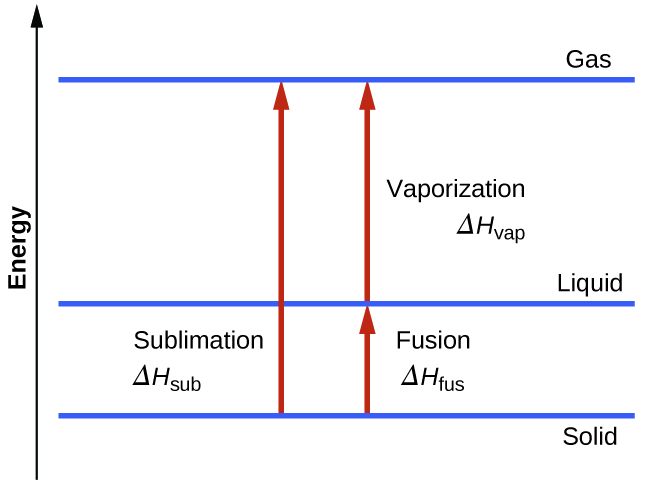
Consider the extent to which intermolecular attractions must be overcome to achieve a given phase transition. Converting a solid into a liquid requires that these attractions be only partially overcome; transition to the gaseous state requires that they be completely overcome. As a result, the enthalpy of fusion for a substance is less than its enthalpy of vaporization. This same logic can be used to derive an approximate relation between the enthalpies of all phase changes for a given substance. Though not an entirely accurate description, sublimation may be conveniently modelled as a sequential two-step process of melting followed by vaporization in order to apply Hess’s Law. Viewed in this manner, the enthalpy of sublimation for a substance may be estimated as the sum of its enthalpies of fusion and vaporization, as illustrated in Figure 13.3h. For example:
Heating and Cooling Curves
In the chapter on thermochemistry, the relation between the amount of heat absorbed or related by a substance, q, and its accompanying temperature change, ΔT, was introduced:
where m is the mass of the substance and c is its specific heat. The relation applies to matter being heated or cooled, but not undergoing a change in state. When a substance is heated or cooled reaches a temperature corresponding to one of its phase transitions, further gain or loss of heat is a result of diminishing or enhancing intermolecular attractions, instead of increasing or decreasing molecular kinetic energies. While a substance is undergoing a change in state, its temperature remains constant. Figure 13.3i shows a typical heating curve.
Consider the example of heating a pot of water to boiling. A stove burner will supply heat at a roughly constant rate; initially, this heat serves to increase the water’s temperature. When the water reaches its boiling point, the temperature remains constant despite the continued input of heat from the stove burner. This same temperature is maintained by the water as long as it is boiling. If the burner setting is increased to provide heat at a greater rate, the water temperature does not rise, but instead the boiling becomes more vigorous (rapid). This behaviour is observed for other phase transitions as well: For example, temperature remains constant while the change of state is in progress.
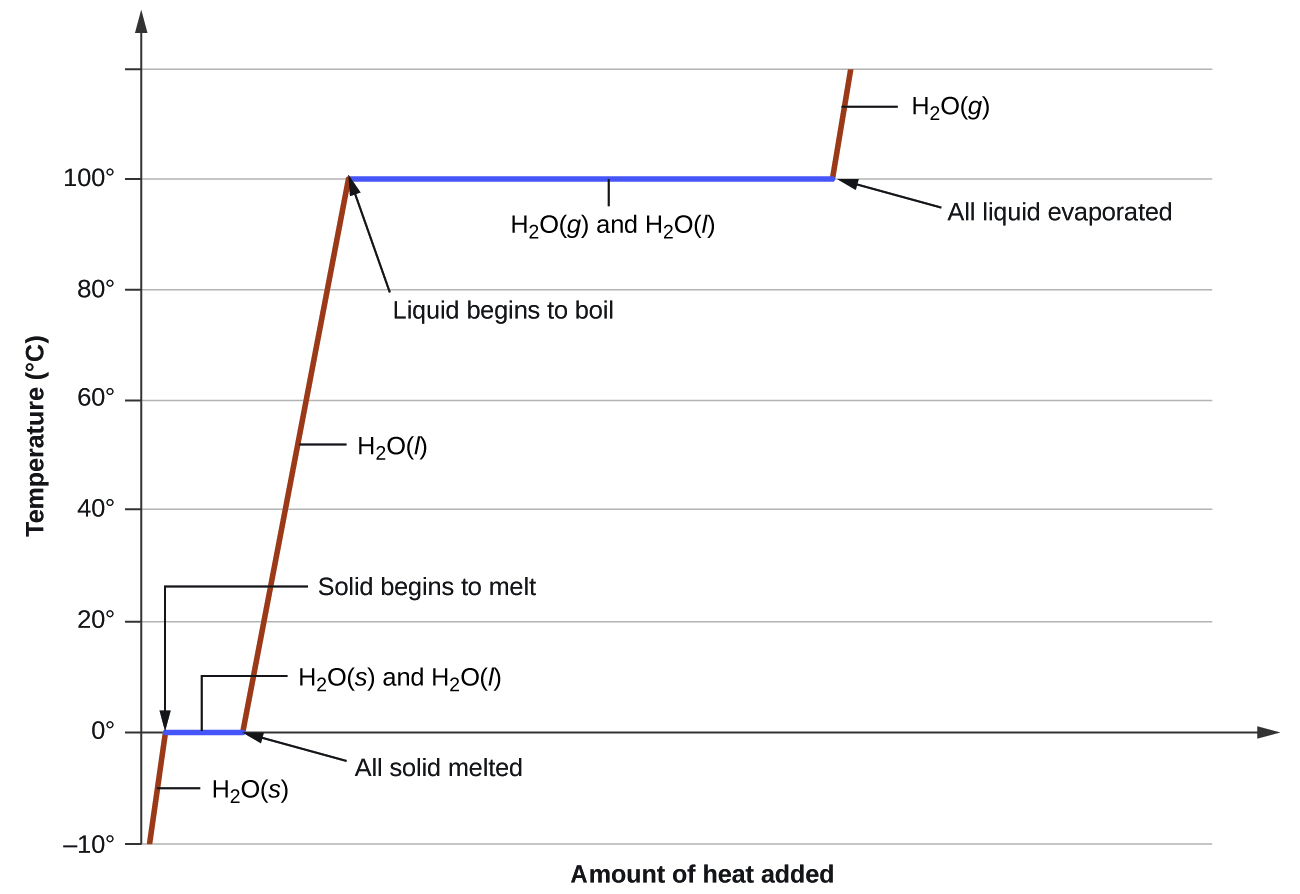
Example 13.3f
Total Heat Needed to Change Temperature and Phase for a Substance
How much heat is required to convert 135 g of ice at −15 °C into water vapour at 120 °C?
Solution
The transition described involves the following steps:
- Heat ice from −15 °C to 0 °C
- Melt ice
- Heat water from 0 °C to 100 °C
- Boil water
- Heat steam from 100 °C to 120 °C
The heat needed to change the temperature of a given substance (with no change in phase) is: q = m ×c × ΔT (see previous chapter on thermochemistry). The heat needed to induce a given change in phase is given by q = n × ΔH.
Using these equations with the appropriate values for specific heat of ice, water, and steam, and enthalpies of fusion and vaporization, we have:
Converting the quantities in J to kJ permits them to be summed, yielding the total heat required:
Exercise 13.3f
What is the total amount of heat released when 94.0 g water at 80.0 °C cools to form ice at −30.0 °C?
Check Your Answer[6]
Exercise 13.3g
Practice using the following PhET simulation: Energy Forms and Changes
Key Equations
- [latex]P = Ae^{-{\Delta}H_{\text{vap}}/RT}\\[0.5em][/latex]
- [latex]\text{ln}\;P = -\frac{{\Delta}H_{\text{vap}}}{RT}\;+\;\text{ln}\;A\\[0.5em][/latex]
- [latex]\text{ln}\;(\frac{P_2}{P_1}) = \frac{{\Delta}H_{\text{vap}}}{R}\;(\frac{1}{T_1}\;-\;\frac{1}{T_2})[/latex]
- [latex]q = mc{\Delta}T[/latex]
Attribution & References
-
All these compounds exhibit hydrogen bonding; these strong IMFs are difficult for the molecules to overcome, so the vapour pressures are relatively low. As the size of molecule increases from methanol to butanol, dispersion forces increase, which means that the vapour pressures decrease as observed:
Pmethanol > Pethanol > Ppropanol > Pbutanol. ↵ - 40 kPa ↵
- 47,782 J/mol = 47.8 kJ/mol ↵
- 30.1 kPa ↵
- 28 kJ ↵
- 40.5 kJ ↵
change from a gaseous to a liquid state
change from liquid state to gaseous state
state of a system in which reciprocal processes are occurring at equal rates
(also, equilibrium vapor pressure) pressure exerted by a vapor in equilibrium with a solid or a liquid at a given temperature
temperature at which the vapor pressure of a liquid equals the pressure of the gas above it
temperature at which a liquid’s vapor pressure equals 1 atm (760 torr)
mathematical relationship between the temperature, vapor pressure, and enthalpy of vaporization for a substance
change from a solid state to a liquid state
change from a liquid state to a solid state
temperature at which the solid and liquid phases of a substance are in equilibrium; see also freezing point
temperature at which the solid and liquid phases of a substance are in equilibrium; see also melting point
change from solid state directly to gaseous state
change from a gaseous state directly to a solid state

