16.3 Ionization of Water
Learning Objectives
By the end of this section, you will be able to:
- Describe the autoionization of water
- Use the ion-product constant for water to calculate hydronium and hydroxide ion concentrations
To begin this chapter, Watch How Polarity makes Water Behave Strangely (3min 51s).
Video Source: TED-Ed. (2013, February 4). How polarity makes water behave strangely – Christina Kleinberg [Video]. YouTube.
Earlier in this chapter, the concept of amphoteric species, such as water, was introduced. Because of its highly polar structures, water can function as either an acid or a base, depending on the nature of the solute dissolved in it. In fact, in pure water or in any aqueous solution, water acts both as an acid and a base. A very small fraction of water molecules donate protons to other water molecules to form hydronium ions and hydroxide ions (Figure 16.3a).
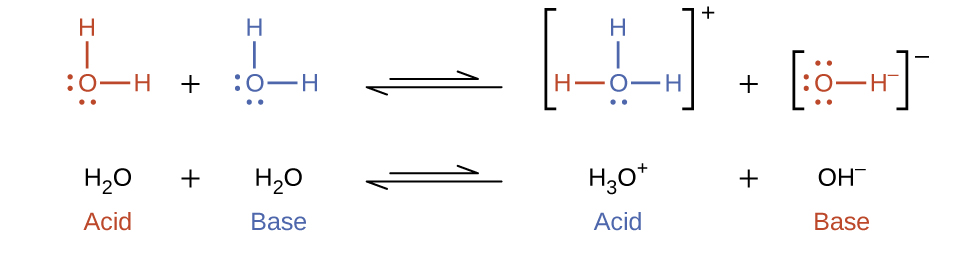
This type of reaction, in which a substance ionizes when one molecule of the substance reacts with another molecule of the same substance, is referred to as autoionization.
To visualize this process in a video simulation, watch Autoionization in Liquid Water (3 min 23s).
Video Source: Akumich (2012, February 22). Autoionization of liquid water. [Video]. YouTube.
Pure water undergoes autoionization to a very slight extent. Only about two out of every 109 molecules in a sample of pure water are ionized at 25 °C. The relationship between products and reactants of any reaction at equilibrium can be expressed by its equilibrium constant, K. The equilibrium constant for the ionization of water is called the ion-product constant for water (Kw):
[latex]\text{H}_2\text{O}(l)\;+\;\text{H}_2\text{O}(l)\;{\leftrightharpoons}\;\text{H}_3\text{O}^{+}(aq)\;+\;\text{OH}^{-}(aq)\\[0.7em] K_{\text{w}} = [\text{H}_3\text{O}^{+}][\text{OH}^{-}][/latex]
The slight ionization of pure water is reflected in the small value of the equilibrium constant; at 25 °C, Kw has a value of 1.0 × 10−14. The process is endothermic, and so the extent of ionization and the resulting concentrations of hydronium ion and hydroxide ion increase with temperature. For example, at 100 °C, the value for Kw is about 5.6 × 10−13, roughly 50 times larger than the value at 25 °C.
Example 16.3a
Ion Concentrations in Pure Water
What are the hydronium ion concentration and the hydroxide ion concentration in pure water at 25 °C?
Solution
The autoionization of water yields the same number of hydronium and hydroxide ions. Therefore, in pure water, [H3O+] = [OH−]. At 25 °C:
So:
The hydronium ion concentration and the hydroxide ion concentration are the same, and we find that both equal 1.0 × 10−7M.
Therefore, at 25 °C, Kw has a value of 1.0 × 10−14.
[latex]K_{\text{w}} = [\text{H}_3\text{O}^{+}][\text{OH}^{-}] = 1.0\;\times\;10^{-14}[/latex]
The degree of autoionization of water and hence the value of Kw changes with temperature, so the equation
[latex]K_{\text{w}} = [\text{H}_3\text{O}^{+}][\text{OH}^{-}] = 1.0\;\times\;10^{-14}[/latex]
is accurate only at room temperature. If a temperature is not given in a question, assume room temperature.
Exercise 16.3a
The ion product of water at 80 °C is 2.4 × 10−13. What are the concentrations of hydronium and hydroxide ions in pure water at 80 °C?
Check Your Answer[1]
Calculating Hydronium and Hydroxide Concentrations in Solutions using Kw
It is important to realize that the autoionization equilibrium for water is established in all aqueous solutions. Pure water is considered a neutral solution. Adding an acid or base to water will not change the position of the equilibrium.
Ion Concentrations in Water
At 25°C,
- In a neutral solution, the [H3O+] = [OH−] = 1.0 x 10-7 M
- In an acidic solution, the concentration of H3O+(aq) is greater than 1.0 x 10-7 M, and thus, its [OH–] will be less than 1.0 x 10-7 M
- In an acidic solution, the [H3O+] > [OH–]
- For basic solutions, the concentration of OH−(aq) is greater than 1.0 x 10-7 M, and thus, its [H3O+] will be less than 1.0 x 10-7 M
- In a basic solution, the [OH–] > [H3O+]
However, remember the product of the two concentrations [H3O+][OH−] is always equal to 1.0 x 10-14 M, no matter whether the aqueous solution is an acid, a base, or neutral:
Kw = [H3O+][OH−] = 1.0 x 10-14 M
Consequently, if you know [H3O+] for a solution, you can use the Kw formula to calculate the [OH−]. Alternatively, if you know [OH−], you can calculate [H3O+]. This means in any given acid/base solution the two concentrations are inversely related: As one concentration increases, the other must decrease, so their product always equals the value of Kw.
Source: “Ion Concentrations in Water” by Jackie MacDonald, CC BY-NC-SA 4.0
Example 16.3b demonstrates the quantitative aspects of this relation between hydronium and hydroxide ion concentrations. At 25°C:
[latex]K_{\text{w}} = [\text{H}_3\text{O}^{+}][\text{OH}^{-}] = 1.0\;\times\;10^{-14}[/latex]
Example 16.3b
The Inverse Proportionality of [H3O+] and [OH−]
A solution of carbon dioxide in water has a hydronium ion concentration of 2.0 × 10−6M. What is the concentration of hydroxide ion at 25 °C?
Solution
We know the value of the ion-product constant for water at 25 °C:
Thus, we can calculate the missing equilibrium concentration.
Rearrangement of the Kw expression yields that [OH−] is directly proportional to the inverse of [H3O+]:
The hydroxide ion concentration in water is reduced to 5.0 × 10−9M as the hydrogen ion concentration increases to 2.0 × 10−6M. This is expected from Le Châtelier’s principle; the autoionization reaction shifts to the left to reduce the stress of the increased hydronium ion concentration and the [OH−] is reduced relative to that in pure water.
A check of these concentrations confirms that our arithmetic is correct:
Exercise 16.3b
What is the hydronium ion concentration in an aqueous solution with a hydroxide ion concentration of 0.001 M at 25 °C?
Check Your Answer[2]
Exercise 16.3c
Practice using the following PhET simulation: pH Scale
Example 16.3c
For the following solutions, determine whether the solution is acidic, basic or neutral.
- A solution that has a [H3O+] = 3.5 x 10-3 M
- A solution that has a [OH–] = 1.0 x 10-7 M
- A solution that has a [H3O+] = 3.5 x 10-12 M
Solution
- Since the solution’s [H3O+] of 3.5 x 10-3 M is greater than 1.0 x 10-7M, the solution is acidic.
- Since the solution’s [OH–] of 1.0 x 10-7M is equal to 1.0 x 10-7M, the solution is neutral.
- Since the solution’s [H3O+] of 3.5 x 10-12 M is less than 1.0 x 10-7M, its [OH–] will be greater 1.0 x 10-7M, which indicates the solution is basic.
Activity Source: “Example 16.3c” created by Jackie MacDonald is licensed under CC BY-NC-SA 4.0.
Exercise 16.3d
Check Your Learning Exercise (Text Version)
For the following solutions, determine whether the solution is acidic, basic or neutral.
- A solution that has a [H3O+] = 2.5 x 10-12 M
- A solution that has a [H3O+] = 9.0 x 10-4 M
- A solution that has a [H3O+] = 1.0 x 10-7 M
- A solution that has a [OH–] = 1.0 x 10-9 M
- A solution that has a [OH–] = 1.0 x 10-7 M
- A solution that has a [OH–] = 4.8 x 10-2 M
Check Your Answer[3]
Source: “Exercise 16.3d” by Jackie MacDonald, licensed under CC BY NC SA 4.0.
Key Equations
- Kw = [H3O+][OH−] = 1.0 × 10−14 (at 25 °C)
Attribution & References
reaction between identical species yielding ionic products; for water, this reaction involves transfer of protons to yield hydronium and hydroxide ions
equilibrium constant for the autoionization of water
The solution in which the concentration of hydroxide ions equals the concentration of hydrogen ions [H3O+] = [OH−]

