Chapter 10 – Review

10.1 Electromagnetic Radiation & 10.2 The Bohr Atom

  1. The light produced by a red neon sign is due to the emission of light by excited neon atoms. Qualitatively describe the spectrum produced by passing light from a neon lamp through a prism.
    Check Answer:     [1]
  2. The laser on a Blu-ray player has a wavelength of 405 nm. In what region of the electromagnetic spectrum is this radiation? What is its frequency?
    Check Answer: [2]
  3. CKUN-FM is a First Nations/community radio station broadcasting at 101.3 FM dial in Christian Island, Ontario, Canada broadcasts at a frequency of 1.013 × 108 s−1 (101.3 MHz) (Wikipedia, 2022). What is the wavelength of these radio waves in meters?
    Check Answer: [3]
  4. FM-95, an FM radio station, broadcasts at a frequency of 9.51 × 107 s−1 (95.1 MHz). What is the wavelength of these radio waves in meters?
    Check Answer: [4]
  5. A bright violet line occurs at 435.8 nm in the emission spectrum of mercury vapour. What amount of energy, in joules, must be released by an electron in a mercury atom to produce a photon of this light?
    Check Answer: [5]
  6. Light with a wavelength of 614.5 nm looks orange. What is the energy, in joules, per photon of this orange light? What is the energy in eV (1 eV = 1.602 × 10−19 J)?
    Check Answer: [6]
  7. Heated lithium atoms emit photons of light with an energy of 2.961 × 10−19 J. Calculate the frequency and wavelength of one of these photons. What is the total energy in 1 mole of these photons? What is the colour of the emitted light?
    Check Answer: [7]
  8. A photon of light produced by a surgical laser has an energy of 3.027 × 10−19 J. Calculate the frequency and wavelength of the photon. What is the total energy in 1 mole of photons? What is the colour of the emitted light?
    Check Answer: [8]
  9. When rubidium ions are heated to a high temperature, two lines are observed in its line spectrum at wavelengths (a) 7.9 × 10−7 m and (b) 4.2 × 10−7 m. What are the frequencies of the two lines? What colour do we see when we heat a rubidium compound?
    Check Answer: [9]
  10. The emission spectrum of cesium contains two lines whose frequencies are (a) 3.45 × 1014 Hz and (b) 6.53 × 1014 Hz. What are the wavelengths and energies per photon of the two lines? What colour are the lines?
    Check Answer: [10]
  11. One of the radiographic devices used in a dentist’s office emits an X-ray of wavelength 2.090 × 10−11 m. What is the energy, in joules, and frequency of this X-ray? Check Answer: [11]
  12. The eyes of certain reptiles pass a single visual signal to the brain when the visual receptors are struck by photons of a wavelength of 850 nm. If a total energy of 3.15 × 10−14 J is required to trip the signal, what is the minimum number of photons that must strike the receptor?
    Check Answer: [12]
  13. RGB colour television and computer displays use cathode ray tubes that produce colours by mixing red, green, and blue light. If we look at the screen with a magnifying glass, we can see individual dots turn on and off as the colours change. Using a spectrum of visible light, determine the approximate wavelength of each of these colours. What is the frequency and energy of a photon of each of these colours?
    Check Answer: [13]
  14. Why is the electron in a Bohr hydrogen atom bound less tightly when it has a quantum number of n = 3 than when it has a quantum number of n = 1?
    Check Answer: [14]
  15. What does it mean to say that the energy of the electrons in an atom is quantized?
    Check Answer: [15]
  16. Using the Bohr model, determine the energy, in joules, necessary to ionize a ground-state hydrogen atom. Use formula [latex]E_n = -\frac{kZ^2}{n^2}[/latex] where Z is the nuclear charge (+1 for hydrogen) and k has a value of 2.179 × 10–18 J. Show your calculations.
    Check Answer: [16]
  17. The electron volt (eV) is a convenient unit of energy for expressing atomic-scale energies. It is the amount of energy that an electron gains when subjected to a potential of 1 volt; 1 eV = 1.602 × 10–19 J. Using the Bohr model, determine the energy, in electron volts, of the photon produced when an electron in a hydrogen atom moves from the orbit with n = 5 to the orbit with n = 2. Use formula [latex]\Delta E = k(\frac{1}{n^2_1} - \frac{1}{n^2_2})[/latex] and k has a value of 2.179 × 10–18 J. Show your calculations.
    Check Answer: [17]
  18. Consider a large number of hydrogen atoms with electrons randomly distributed in the n = 1, 2, 3, and 4 orbits.
    Check Answer: [18]

    1. How many different wavelengths of light are emitted by these atoms as the electrons fall into lower-energy orbitals?
    2. Calculate the lowest and highest energies of light produced by the transitions described in part (a). Use formula [latex]\Delta E = k(\frac{1}{n^2_1} - \frac{1}{n^2_2})[/latex] and k has a value of 2.179 × 10–18 J.
    3. Calculate the frequencies and wavelengths of the light produced by the transitions described in part (b). Using Figure 10.1c: The Electromagnetic Spectrum as a reference, specify the type of electromagnetic radiation emitted in each energy jump in part (b). Use E=hf to calculate frequency, where the constant of proportionality, h, is called Planck’s constant h = 6.626 × 10–34 joule-seconds (J-s). Use equation c = λν to solve for the wavelength: [latex]\lambda = \frac{c}{\nu}[/latex]
  19. How are the Bohr model and the Rutherford model of the atom similar? How are they different?
    Check Answer: [19]
  20. The spectra of hydrogen and of iron are shown in Figures 10.2c and 10.2d Comparing Emission Line Spectra of White Light and Light from Various Elements. When referencing these figures, recall that 1 angstrom = 0.1 nm = 1 × 10–10 m. Answer the following questions: (a) What causes the lines in these spectra? (b) Why are the colours of the lines different? (c) Suggest a reason for the observation that the spectrum of iron is more complicated than the spectrum of hydrogen.
    Check Answer: [20]

10.3 Wave Nature of Matter & 10.4 Quantum Mechanical Model of the Atom 

  1. How are the Bohr model and the quantum mechanical model of the hydrogen atom similar? How are they different?
    Check Answer: [21]
  2. Summarize the allowed values for each of the four quantum numbers: n, l, ml, and ms?
    Check Answer: [22]
  3. Describe the properties of an electron associated with each of the following four quantum numbers: n, l, ml, and ms.
    Check Answer: [23]
  4. Identify the subshell in which electrons with the following quantum numbers are found:
    Check Answer: [24]

    1. n = 2, l = 1
    2. n = 4, l = 2
    3. n = 6, l = 0
  5. Which of the subshells described in the previous question contain degenerate orbitals? How many degenerate orbitals are in each?
    Check Answer: [25]
  6. Identify the subshell in which electrons with the following quantum numbers are found:
    Check Answer: [26]

    1. n = 3, l = 2
    2. n = 1, l = 0
    3. n = 4, l = 3
  7. Which of the subshells described in the previous question contain degenerate orbitals? How many degenerate orbitals are in each?
    Check Answer: [27]
  8. (a) How many different types of orbitals are found in principal energy level 2? Provide the letter name for these subshells. (b) How many different types of orbitals are found in principal energy level 4? Provide the letter name for these subshells.
    Check Answer: [28]
  9. What is the smallest possible n value for an s orbital? p orbital? d orbital? f orbital?
    Check Answer: [29]
  10. Write the maximum number of electrons allowed in the indicated sublevels: s sublevel? p sublevel? d sublevel? f sublevel?
    Check Answer: [30]
  11. (a) What is the maximum number of electrons that can occupy (a) the first principal energy level? (b) the second principal energy level? (c) the third principal energy level? (d) the fourth principal energy level?
    Check Answer: [31]
  12. State the Heisenberg uncertainty principle. Describe briefly what the principle implies.
    Check Answer: [32]
  13. Write a set of quantum numbers for each of the electrons with an n of 4 in a Se atom.
    Check Answer: [33]

10.5 Atomic Structures Of The First 20 Elements. 

  1. 100% pure Canadian maple syrup disguises nutrients in a sweet natural taste. One 30 ml (2 Tablespoons) serving of pure maple syrup contains 35% of the Daily Value of Manganese. It is also a source of calcium and potassium. (Source: Quebec Maple Syrup Producers (QMSP), 2021). Write the complete electron configurations and noble gas configurations for manganese, calcium, and potassium. Check Answer: [34]
  2. Water and electrolyte balance is important in maintaining homeostasis in the human body. The main electrolytes (ions) in the body that we get from the food we eat and fluids we drink include sodium, calcium, potassium, chloride, and magnesium. (a) Write the complete electron configurations for the following ions: sodium, magnesium, and chloride. (b) What do you notice about these ions? Check Answer: [35]
  3. Using complete subshell notation (not abbreviations, 1s22s22p6, and so forth), predict the electron configuration of each of the following atoms: Check Answer: [36]
    1. C (z = 6)
    2. P (z = 15)
    3. V (z = 23)
    4. Sb (z = 51)
    5. Sm (z = 62)
  4. Using complete subshell notation (1s22s22p6, and so forth), predict the electron configuration of each of the following atoms: Check Answer: [37]
    1. N
    2. Si
    3. Fe
    4. Te
    5. Tb
  5. Draw the orbital diagram for the valence shell of each of the following atoms: Check Answer: [38]
    1. C
    2. P
    3. V
    4. Sb
  6. Use an orbital diagram to describe the electron configuration of the valence shell of each of the following atoms:
    Check Answer: [39]

    1. N
    2. Si
    3. Fe
    4. Te
  7. Using complete subshell notation (1s22s22p6, and so forth), predict the electron configurations of the following ions.
    Check Answer: [40]

    1. N3–
    2. Ca2+
    3. S–
    4. Cs2+
    5. Fe3+
    6. Cd2+
  8. Which atom has the electron configuration 1s22s22p63s23p64s23d104p65s24d2?
    Check Answer: [41]
  9. Which atom has the electron configuration 1s22s22p63s23p64s23d7?
    Check Answer: [42]
  10. Which ion with a +1 charge has the electron configuration 1s22s22p63s23p63d104s24p6? Which ion with a –2 charge has this configuration?
    Check Answer: [43]
  11. Which of the following atoms has only two unpaired electrons?
    Check Answer: [44]

    1. Mg
    2. Si
    3. S
    4. Ge
  12. Which atom would be expected to have a half-filled 6p subshell?
    Check Answer: [45]
  13. Which atom would be expected to have a half-filled 4s subshell?
    Check Answer: [46]
  14. In one area of Australia, the cattle did not thrive despite the presence of suitable forage. An investigation showed the cause to be the absence of sufficient cobalt in the soil. Cobalt forms cations in two oxidation states, Co2+ and Co3+. Write the electron structure of the two cations.
    Check Answer: [47]
  15. Thallium (Z = 81) was used as a poison in the Agatha Christie mystery story “The Pale Horse.” Thallium has two possible cationic forms, +1 and +3. The +1 compounds are the more stable. Write the electron structure of the +1 cation of thallium.
    Check Answer: [48]
  16. Cobalt–60 and iodine–131 are radioactive isotopes commonly used in nuclear medicine. How many protons, neutrons, and electrons are in atoms of these isotopes? Write the complete electron configuration for each isotope.
    Check Answer: [49]

10.6 Atomic Properties And Periodic Table Trends

  1. Based on their positions in the periodic table, predict which has the smallest atomic radius: Mg, Sr, Si, Cl, I.
    Check Answer: [50]
  2. Based on their positions in the periodic table, predict which has the largest atomic radius: Li, Rb, N, F, I.
    Check Answer: [51]
  3. Based on their positions in the periodic table, predict which has the largest first ionization energy: Mg, Ba, B, O, Te.
    Check Answer: [52]
  4. Based on their positions in the periodic table, predict which has the smallest first ionization energy: Li, Cs, N, F, I.
    Check Answer: [53]
  5. Based on their positions in the periodic table, rank the following atoms in order of increasing first ionization energy: F, Li, N, Rb.
    Check Answer: [54]
  6. Based on their positions in the periodic table, rank the following atoms or compounds in order of increasing first ionization energy: Mg, O, S, Si.
    Check Answer: [55]
  7. Atoms of which group in the periodic table have a valence shell electron configuration of ns2np3?
    Check Answer: [56]
  8. Atoms of which group in the periodic table have a valence shell electron configuration of ns2?
    Check Answer: [57]
  9. Based on their positions in the periodic table, list the following atoms in order of increasing radius: Mg, Ca, Rb, Cs.
    Check Answer: [58]
  10. Based on their positions in the periodic table, list the following atoms in order of increasing radius: Sr, Ca, Si, Cl.
    Check Answer: [59]
  11. Based on their positions in the periodic table, list the following ions in order of increasing radius: K+, Ca2+, Al3+, Si4+.
    Check Answer: [60]
  12. List the following ions in order of increasing radius: Li+, Mg2+, Br–, Te2–.
    Check Answer: [61]
  13. Which atom and/or ion is/are isoelectronic with Br+: Se2+, Se, As–, Kr, Ga3+, Cl–?
    Check Answer: [62]
  14. Which of the following atoms and ions is/are isoelectronic with S2+: Si4+, Cl3+, Ar, As3+, Si, Al3+?
    Check Answer: [63]
  15. Compare both the numbers of protons and electrons present in each to rank the following ions in order of increasing radius: As3–, Br–, K+, Rb+, Mg2+.
    Check Answer: [64]
  16. The ionic radii of the ions S2–, Cl–, and K+ are 184, 181, 138 pm respectively. Explain why these ions have different sizes even though they contain the same number of electrons.
    Check Answer: [65]
  17. Which main group atom would be expected to have the lowest second ionization energy?
    Check Answer: [66]
  18. Explain why Al is a member of group 13 rather than group 3.
    Check Answer: [67]

Attribution & References

Except where otherwise noted, this page is adapted by Jackie MacDonald from:

References

Quebec Maple Syrup Producers (QMSP). (2021, December 27). Nutritional benefits. Pure Maple from Canada. Retrieved December 1, 2022, from https://www.puremaplefromcanada.com/nutrition/).

Wikipedia contributors. (2022, February 1). CKUN-FM. Wikipedia. https://en.wikipedia.org/wiki/CKUN-FM

  1. The spectrum consists of coloured lines, at least one of which (probably the brightest) is red. ↵
  2. Visible light spectrum; v = 6.7 x 1014 s−1 or Hz ↵
  3. λ = 2.960 m ↵
  4. 3.15 m ↵
  5. 4.558 × 10−19 J; Watch "6.4 | A bright violet line occurs at 435.8 nm in the emission spectrum of mercury vapor" for an explanation of the solution to this question ↵
  6. 3.233 × 10−19 J; 2.018 eV; Watch "6.5 | Light with a wavelength of 614.5 nm looks orange" for an explanation of the solution to this question ↵
  7. v = 4.469 × 1014 s−1; λ = 6.708 × 10−7 m or 670.8 nm; Total Energy in 1 mole of photons = 1.783 × 105 J/mol or J mol−1; Colour of light = Red; Watch "6.6 | Heated lithium atoms emit photons of light with an energy of 2.961 × 10^−19 J." for an explanation of the solution to this question. ↵
  8. ν = 4.568 × 1014 s−1; λ = 6.563 × 10−7 m or 656.3 nm; Total Energy in 1 mole of photons = 1.823 × 105 J mol−1; Colour of light = red ↵
  9. (a) v = 3.8 x 1014 s−1 or Hz; (b) v = 7.1 × 1014 s−1 or Hz; The colour of (a) is red since wavelength is 790 nm; (b) is purple/violet/ deep blue since wavelength is 420 nm; Watch "6.8 | When rubidium ions are heated to a high temperature" for an explanation of solution to this question. ↵
  10. (a) λ = 8.69 × 10−7 m; E = 2.29 × 10−19 J; (b) λ = 4.59 × 10−7 m; E = 4.33 × 10−19 J; The colour of (a) is red since wavelength is 869 nm; (b) is blue since wavelength is 459 nm; Watch "6.9 | The emission spectrum of cesium contains two lines" for an explanation of solution to this question. ↵
  11. E = 9.502 × 10−15 J; ν = 1.434 × 1019 s−1 or Hz; Watch "6.11 | One of the radiographic devices used in a dentist's office" for an explanation of solution to this question. ↵
  12. Minimum number of photons required = 1.4 × 105 photons; Watch "6.12 | The eyes of certain reptiles" for an explanation of solution to this question.  ↵
  13. If use wavelength of 680 nm for Red: v = 4.4 × 1014 s−1 or Hz and E = 2.9 × 10−19 J. If use wavelength of 520 nm for Green: v = 5.8 × 1014 s−1 or Hz and E = 3.8 × 10−19 J. If use wavelength of 440nm for Blue: v = 6.8 × 1014 s−1 or Hz and E = 4.5 × 10−19 J. Somewhat different numbers are also possible if you chose different wavelengths for each colour. Watch "6.13 | RGB color television and computer displays" for an explanation of solution to this question. ↵
  14. An n of 3 indicates that an electron in the hydrogen atom is in the third energy level, which is further from the nucleus than the first energy level (n=1). The Bohr model uses the theory of electrostatic attraction between the positively charged nucleus and the negatively charge electron in its orbital. The closer an electron is to the nucleus the more closely it is held by the nucleus. The farther an electron is from the nucleus ( in higher shells or energy levels), the less the electrostatic attraction of an electron to the nucleus due to the shielding effect; hence, an electron in energy level 3 will be bound less tightly than an electron in energy level 1. ↵
  15. Quantized energy means that the electrons can possess only certain discrete energy values; values between those quantized values are not permitted. ↵
  16. En = -2.179 × 10-18 J ↵
  18. [latex]\begin{array}{r @{{}={}}l} E & E_2 - E_5 = 2.179 \times 10^{-18} (\frac{1}{n^2_2} - \frac{1}{n^2_5}) \;\text{J} \\[1em] & 2.179 \times 10^{-18} (\frac{1}{2^2} - \frac{1}{5^2}) = 4.576 \times 10^{-19} \;\text{J} \\[1em] & \frac{4.576 \times 10^{-19} \;\rule[0.5ex]{0.4em}{0.1ex}\hspace{-0.4em}\text{J}}{1.602 \times 10^{-19} \;\rule[0.5ex]{0.4em}{0.1ex}\hspace{-0.4em}\text{J eV}^{-1}} = 2.856 \;\text{eV} \end{array}[/latex]Watch "6.19 | The electron volt (eV) is a convenient unit of energy" for an explanation of solution to this question. ↵
  19. (a) 6 different wavelengths. (b) Lowest energy would be a jump from n = 4 to n = 3, and the change in energy is -1.06 × 10-19 J ; the highest energy would be a jump from n = 4 to n = 1, and the change in energy is -2.04 × 10-18 J. Recall that a negative energy value means that energy is being released. (c) For the lowest energy jump (n =4 to n =3), v = 1.60 × 1014 s−1 and λ = 1.87 × 10-6 m, which is indicative of infrared radiation (1870 nm); for the highest energy jump (n =4 to n =1), v = 3.08 × 1015 s−1 and λ = 9.73 × 10-8 m, which is indicative of UV radiation (97.3 nm). Watch "6.28 | Consider a large number of hydrogen atoms with electrons" for an explanation of solution to this question. ↵
  20. Both involve a relatively heavy nucleus with electrons moving around it, although strictly speaking, the Bohr model works only for one-electron atoms or ions. According to classical mechanics, the Rutherford model predicts a miniature “solar system” with electrons moving about the nucleus in circular or elliptical orbits that are confined to planes. If the requirements of classical electromagnetic theory that electrons in such orbits would emit electromagnetic radiation are ignored, such atoms would be stable, having constant energy and angular momentum, but would not emit any visible light (contrary to observation). If classical electromagnetic theory is applied, then the Rutherford atom would emit electromagnetic radiation of continually increasing frequency (contrary to the observed discrete spectra), thereby losing energy until the atom collapsed in an absurdly short time (contrary to the observed long-term stability of atoms). The Bohr model retains the classical mechanics view of circular orbits confined to planes having constant energy and angular momentum, but restricts these to quantized values dependent on a single quantum number, n. The orbiting electron in Bohr’s model is assumed not to emit any electromagnetic radiation while moving about the nucleus in its stationary orbits, but the atom can emit or absorb electromagnetic radiation when the electron changes from one orbit to another. Because of the quantized orbits, such “quantum jumps” will produce discrete spectra, in agreement with observations. ↵
  21. (a) Every line represents a specific wavelength of discrete energies that is emitted when electrons transition from a higher energy shell to a lower energy shell. The emitted light corresponds to energies of the specific electrons. (b) The colours of the lines are different because different wavelengths equate to different discrete energies that represent a specific colour. (c) The line spectrum of iron is more complicated than hydrogen (which only has four lines). Hydrogen (atomic number = 1) only has 1 electron, where iron (atomic number = 26) has 26 electrons. As a result, iron has more energy shell transition possibilities for its electrons and will have a more complicated emission line spectra than hydrogen. ↵
  22. Both models have a central positively charged nucleus with electrons moving about the nucleus in accordance with the Coulomb electrostatic potential. The Bohr model assumes that the electrons move in circular orbits that have quantized energies, angular momentum, and radii that are specified by a single quantum number, n = 1, 2, 3, …, but this quantization is an ad hoc assumption made by Bohr to incorporate quantization into an essentially classical mechanics description of the atom. Bohr also assumed that electrons orbiting the nucleus normally do not emit or absorb electromagnetic radiation, but do so when the electron switches to a different orbit. In the quantum mechanical model, the electrons do not move in precise orbits (such orbits violate the Heisenberg uncertainty principle) and, instead, a probabilistic interpretation of the electron’s position at any given instant is used, with a mathematical function ψ called a wavefunction that can be used to determine the electron’s spatial probability distribution. These wavefunctions, or orbitals, are three-dimensional stationary waves that can be specified by three quantum numbers that arise naturally from their underlying mathematics (no ad hoc assumptions required): the principal quantum number, n (the same one used by Bohr), which specifies shells such that orbitals having the same n all have the same energy and approximately the same spatial extent; the angular momentum quantum number l, which is a measure of the orbital’s angular momentum and corresponds to the orbitals’ general shapes, as well as specifying subshells such that orbitals having the same l (and n) all have the same energy; and the orientation quantum number m, which is a measure of the z component of the angular momentum and corresponds to the orientations of the orbitals. The Bohr model gives the same expression for the energy as the quantum mechanical expression and, hence, both properly account for hydrogen’s discrete spectrum (an example of getting the right answers for the wrong reasons, something that many chemistry students can sympathize with), but gives the wrong expression for the angular momentum (Bohr orbits necessarily all have non-zero angular momentum, but some quantum orbitals [s orbitals] can have zero angular momentum). (Answer Source: Answer to this question was retrieved from Problem 2.3.7 in General Chemistry II (Addie Clark). LibreTexts. licensed under CC BY-NC-SA 3.0 ) ↵
  23. The principal quantum number (n) values are  1, 2, 3, 4, and so on. The angular momentum quantum number (l) can be any integer between 0 and n - 1. It specifies the type of subshell, specifically the 3D shape of an orbital (0 = s; 1 = p; 2 = d; 3 = f; and so on. If n = 3, for example, l can be either 0, 1, or 2. The third energy level can have electrons occupying s, p or d orbitals. The magnetic quantum number (ml) can be any integer between -l and +l. This number divides the subshell into individual orbitals which hold two electrons per orbital; there are 2l+1 orbitals in each subshell. If l = 2, ml can be either -2, -1, 0, +1, or +2 (a d subshell has 5 orbitals, each can contain 2 electrons). Spin quantum number (ms) specifies the orientation of the spin axis of an electron.  An electron can only spin one of two ways where ms = [latex]\frac{1}{2}[/latex] (up) or [latex]- \frac{1}{2}[/latex] (down).  If two electrons share the same orbital, they must have opposite spins. ↵
  24. n determines the general range for the value of energy (principal energy level) and the probable distances that the electron can be from the nucleus. l determines the shape of the orbital. ml determines the orientation of the orbitals of the same l value with respect to one another; it divides subshell into individual orbitals, which hold two electrons per orbital (there are 2l+1 orbitals in each subshell). ms determines the spin of an electron. ↵
  25. (a) 2p; (b) 4d; (c) 6s ↵
  26. The orbitals which have the same energy [belong to the same subshell and shell (energy level, n)] are called degenerate orbitals. Therefore, 2p contains 3 degenerate orbitals; 4d contains 5 degenerate orbitals; 6s is not degenerate. ↵
  27. (a) 3d; (b) 1s (c) 4f ↵
  28. The orbitals which have the same energy [belong to the same subshell and shell (energy level, n)] are called degenerate orbitals. Therefore, 3d contains 5 degenerate orbitals; 1s is not degenerate; 4f contains 7 degenerate orbitals. ↵
  29. n = 2 has two possible subshells s and p; n = 4 has four possible subshells s, p, d and f. ↵
  30. The smallest possible n value for an s orbital is 1s, p orbital is 2p, d orbital is 3d, f orbital is 4f. ↵
  31. s sublevel electron capacity is 2 electrons; p sublevel electron capacity is 6 electrons; d sublevel electron capacity is 10 electrons; f sublevel electron capacity is 14 electrons ↵
  32. Use electron capacity for a given energy level (shell) =  2n2 (a) the first principal energy level can fit 2(1)2 = 2 electrons; (b) the second principal energy level can fit 2(2)2 = 8 electrons; (c) the third principal energy level can fit 2(3)2 = 18 electrons; (d) the fourth principal energy level can fit 2(4)2 = 32 electrons ↵
  33. Heisenberg’s uncertainty principle states that for particles exhibiting both particle and wave nature, It is fundamentally impossible to accurately determine both the position and velocity (momentum of a particle at the same time. The more precise our measurement of position is, the less accurate will be our momentum measurement and vice-versa ↵
  34. n l ml s
    4 0 0 [latex]+\frac{1}{2}[/latex]
    4 0 0 [latex]-\frac{1}{2}[/latex]
    4 1 −1 [latex]+\frac{1}{2}[/latex]
    4 1 0 [latex]+\frac{1}{2}[/latex]
    4 1 +1 [latex]+\frac{1}{2}[/latex]
    4 1 −1 [latex]-\frac{1}{2}[/latex]
    NOTE: Selenium (Se) has 34 electrons, 6 of which are valence electrons in the fourth principal energy level. The quantum numbers for these 6 valence electrons are shown in the Table. Two electrons are found in the 4s orbital, the other four are found dispersed amongst the three 4p orbitals. ↵
  35. manganese - 1s22s22p63s23p64s23d5,  [Ar]4s23d5; calcium - 1s22s22p63s23p64s2, [Ar]4s2; potassium - 1s22s22p63s23p64s1, [Ar]4s1 ↵
  36. (a) sodium ion (Na+) - 1s22s22p6; magnesium (Mg2+) - 1s22s22p6; chlorine (Cl-) - 1s22s22p63s23p6; (b) Both the sodium ion and magnesium ion have the same electron configurations as their closest noble gas, neon (Ne), which all have 10 electrons. A chlorine ion has the same electron configuration as its closest noble gas, argon (Ar), with 18 electrons. ↵
  37. (a) C - 1s22s22p2; P - 1s22s22p63s23p3; V - 1s22s22p63s23p64s23d3; Sb - 1s22s22p63s23p64s23d104p65s24d105p3; Sm - 1s22s22p63s23p64s23d104p65s24d105p66s24f6 ↵
  38. (a) 1s22s22p3; (b) 1s22s22p63s23p2; (c) 1s22s22p63s23p64s23d6; (d) 1s22s22p63s23p64s23d104p65s24d105p4; (e) 1s22s22p63s23p64s23d104p65s24d105p66s24f9 ↵
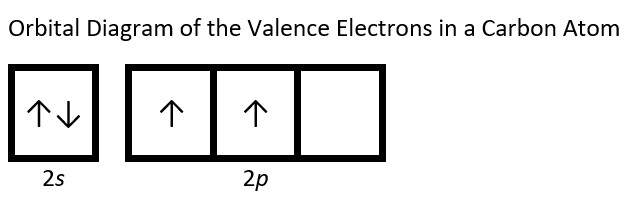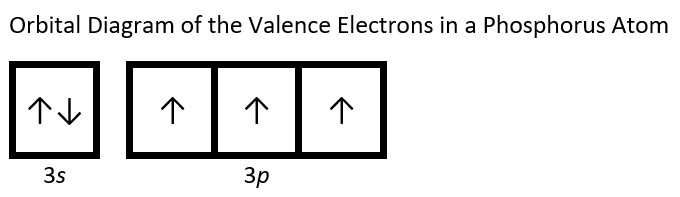  39. (a) CThe orbital diagram of the valence electrons in a carbon atom is shown. There is a total of four valence electrons, two of which fill the 2s orbital and the other two begin to fill the 2p orbitals. An up arrow or down arrow is used to represent an electron. If two electrons share the same orbital, one arrow points up and the other down to show they have opposite spins.(b) PThe orbital diagram of the valence electrons in a phosphorus atom is shown. The valence electrons fill the 3s orbital, and 3 electrons fill the 3p orbital. An up arrow or down arrow is used to represent an electron. 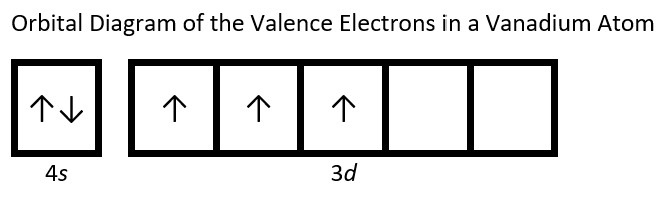If two electrons share the same orbital, one arrow points up and the other down to show they have opposite spins.(c) VThe orbital diagram of the valence electrons in a vanadium atom is shown. There are five valence electrons in total. Two fill the 4s orbital and three electrons fill the 3d orbitals. An up arrow or down arrow is used to represent an electron. If two electrons share the same orbital, one arrow points up and the other down to show they have opposite spins.(d) SbThe orbital diagram of the valence electrons in an antimony atom is shown. There are five valence electrons in total (the 4d orbital is filled completely and are not considered valence electrons). Two fill the 5s orbital and three electrons fill the 5p orbitals. An up arrow or down arrow is used to represent an electron. If two electrons share the same orbital, one arrow points up and the other down to show they have opposite spins. ↵
  40. (a) N

    This figure includes a square followed by 3 squares all connected in a single row. The first square is labeled below as, “2 s.” The connected squares are labeled below as, “2 p.” The first square has a pair of half arrows: one pointing up, and the other down. Each of the remaining squares contains a single upward pointing arrow.

    (b) Si This figure includes a square followed by 3 squares all connected in a single row. The first square is labeled below as, “2 s.” The connected squares are labeled below as, “2 p.” The first square has a pair of half arrows: one pointing up and the other down. The first two squares in the row of connected squares contain a single upward pointing arrow. The third square is empty. (c) Fe This figure includes a square followed by 5 squares all connected in a single row. The first square is labeled below as, “4 s.” The connected squares are labeled below as, “3 d.” The first square and the left-most square in the row of connected squares each has a pair of half arrows: one pointing up and the other down. Each of the remaining squares contains a single upward pointing arrow. (d) Te This figure includes a square followed by 3 squares all connected in a single row. The first square is labeled below as, “5 s superscript 2.” The connected squares are labeled below as, “5 p. superscript 4.” The first square and the left-most square in the row of connect squares each has a pair of half arrows: one pointing up and the other down. Each of the remaining squares contains a single upward pointing arrow. ↵
  41. (a) 1s22s22p6; (b) 1s22s22p63s23p6; (c) 1s22s22p63s23p5; (d) 1s22s22p63s23p64s23d104p65s24d105p5; (e) 1s22s22p63s23p63d5; (f) 1s22s22p63s23p64s23d104p64d10 ↵
  42. Zr, Zicronium ↵
  43. Co, Cobalt ↵
  44. Rb+1 (Rubidium ion); Se2- (Selenium Ion) ↵
  45. answer (b) and (d) are correct. Silicon and Germanium both have only 2 unpaired electrons. ↵
  46. Bi, Bismuth ↵
  47. K, Potassium ↵
  48. Co2+ - 1s22s22p63s23p63d7; Co3+ - 1s22s22p63s23p63d6 ↵
  49. 1s22s22p63s23p63d104s24p64d105s25p66s24f145d10 ↵
  50. Cobalt (Co) has 27 protons, 27 electrons, and 33 neutrons: 1s22s22p63s23p64s23d7. Iodine (I) has 53 protons, 53 electrons, and 78 neutrons: 1s22s22p63s23p63d104s24p64d105s25p5 ↵
  51. Cl ↵
  52. Rb ↵
  53. O ↵
  54. Cs ↵
  55. Rb < Li < N < F ↵
  56. Mg < Si < S < O ↵
  57. 15 (5A) ↵
  58. 2 (2A) Alkaline Earth Metals ↵
  59. Mg < Ca < Rb < Cs ↵
  60. Cl < Si < Ca < Sr ↵
  61. Si4+ < Al3+ < Ca2+ < K+ ↵
  62. Li+, Mg2+, Br–, Te2– ↵
  63. Se, As− (all have 34 electrons) ↵
  64. Cl3+, Si (all have 14 electrons) ↵
  65. Mg2+ < K+ < Rb+ < Br– < As3– ↵
  66. Even though all these options have the same number of electrons, they have different numbers of protons, which determines their size. An increase in protons, increases the positive charge inside the nucleus of the atom, which has a greater attraction and pull of those electrons. When comparing atoms with the same number of electrons, the greater the atomic number, the smaller the radius. ↵
  67. Ra; Watch "6.85 | Which main group atom would be expected to have the lowest second ionization energy?" for an explanation of the solution to the math portion of this question visit ↵
  68. The periodic table is arranged in accordance with increasing atomic number (increasing number of protons and electrons). The groups are arranged according to their chemical behaviours, which is dictated by the number of valence electrons typical for that neutral element. Based on the rules of orbital filling of electrons, aluminum has 13 electrons to fill its orbitals. Al is a p-block element, and electrons must fill 3p block before 4s or 3d. The group 3 elements are d- block elements, which are also known as transition elements. This is why Al does not have any properties like d-block elements; rather, Al has similar properties of elements found in group 13 (3A). ↵

License

Icon for the Creative Commons Attribution 4.0 International License

Enhanced Introductory College Chemistry Copyright © 2023 by Gregory Anderson; Caryn Fahey; Jackie MacDonald; Adrienne Richards; Samantha Sullivan Sauer; J.R. van Haarlem; and David Wegman is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book