16.4 Introduction to pH and pOH
Learning Objectives
- Explain the characterization of aqueous solutions as acidic, basic, or neutral
- Express hydronium and hydroxide ion concentrations on the pH and pOH scales
- Perform calculations relating pH and pOH
As discussed earlier, hydronium and hydroxide ions are present both in pure water and in all aqueous solutions, and their concentrations are inversely proportional as determined by the ion product of water (Kw). The concentrations of these ions in a solution are often critical determinants of the solution’s properties and the chemical behaviours of its other solutes, and specific vocabulary has been developed to describe these concentrations in relative terms. A solution is neutral if it contains equal concentrations of hydronium and hydroxide ions; acidic if it contains a greater concentration of hydronium ions than hydroxide ions; and basic if it contains a lesser concentration of hydronium ions than hydroxide ions. To assist with informing users of a substance’s acidity or basicity (alkalinity), one can calculate the pH of the substance and reference it on the pH scale. For a brief introduction into the pH scale and how it is used, Watch The pH Scale Explained (5min 54s).
Video Source: Chem Academy. (2015, April 28). The pH scale explained. [Video]. YouTube.
Introduction to the pH Scale
The pH scale is a scale of acidity ranging 0 to 14 (but not always). It indicates how acidic or basic a solution is. You can use pH to make a quick determination whether a given aqueous solution is acidic, basic, or neutral. Since the pH of a substance is dependent on hydronium ion concentration, [H3O+], the following conclusions (at standard temperature of 25 °C) can be inferred:
- If pH < 7, then the solution is acidic.
- If pH = 7, then the solution is neutral.
- If pH > 7, then the solution is basic.
Exercise 16.4a
Check Your Learning Exercise (Text Version)
Label each solution as acidic, basic, or neutral based only on the given pH value:
- Household bleach, pH = 12.6
- Lime Juice, pH = 2.3
- Milk of Magnesia, pH = 10.5
- Pure Water, pH = 7
- Vinegar, pH = 2.5
- Baking soda, pH = 8.5
Check Your Answer[1]
Source: “Exercise 16.4a” by Jackie MacDonald, licensed under CC BY-NC-SA 4.0.
Formulas for Calculating pH, pOH, [H3O+], and [OH–]
A common means of expressing quantities, the values of which may span many orders of magnitude, is to use a logarithmic scale. One such scale that is very popular for chemical concentrations and equilibrium constants is based on the p-function, defined as shown where “X” is the quantity of interest and “log” is the base-10 logarithm:
The pH of a solution is therefore defined as shown here, where [H3O+] is the molar concentration of hydronium ion in the solution:
[latex]\text{pH} = -\text{log[H}_3\text{O}^{+}][/latex]
Rearranging this equation to isolate the hydronium ion molarity yields the equivalent expression:
[latex][\text{H}_3\text{O}^{+}] = 10^{-\text{pH}}[/latex]
Likewise, the hydroxide ion molarity may be expressed as a p-function, or pOH:
[latex]\text{pOH} = -\text{log[OH}^{-}][/latex]
or
[latex][\text{OH}^{-}] = 10^{-\text{pOH}}[/latex]
Finally, the relation between these two ion concentration expressed as p-functions is easily derived from the Kw expression:
Kw = [H3O+][OH–]
-log Kw = -log([H3O+][OH–]) = -log[H3O+]+ -log[OH–]
pKw = pH + pOH
At 25 °C, the value of Kw is 1.0 × 10−14, and so:
14.00 = pH + pOH
As was shown in Example 16.3a, Brønsted-Lowry Acids and Bases, the hydronium ion molarity in pure water (or any neutral solution) is 1.0 × 10−7M at 25 °C. The pH and pOH of a neutral solution at this temperature are therefore:
And so, at this temperature, acidic solutions are those with hydronium ion molarities greater than 1.0 × 10−7M and hydroxide ion molarities less than 1.0 × 10−7M (corresponding to pH values less than 7.00 and pOH values greater than 7.00). Basic solutions are those with hydronium ion molarities less than 1.0 × 10−7M and hydroxide ion molarities greater than 1.0 × 10−7M (corresponding to pH values greater than 7.00 and pOH values less than 7.00).
Since the autoionization constant Kw is temperature dependent, these correlations between pH values and the acidic/neutral/basic adjectives will be different at temperatures other than 25 °C. For example, the hydronium molarity of pure water at 80 °C is 4.9 × 10−7M, which corresponds to pH and pOH values of:
At this temperature, then, neutral solutions exhibit pH = pOH = 6.31, acidic solutions exhibit pH less than 6.31 and pOH greater than 6.31, whereas basic solutions exhibit pH greater than 6.31 and pOH less than 6.31. This distinction can be important when studying certain processes that occur at nonstandard temperatures, such as enzyme reactions in warm-blooded organisms. Unless otherwise noted, references to pH values are presumed to be those at standard temperature (25 °C) (Table 16.4a).
| Classification | Relative Ion Concentrations | pH at 25 °C |
|---|---|---|
| acidic | [H3O+] > [OH−] | pH < 7 |
| neutral | [H3O+] = [OH−] | pH = 7 |
| basic | [H3O+] < [OH−] | pH > 7 |
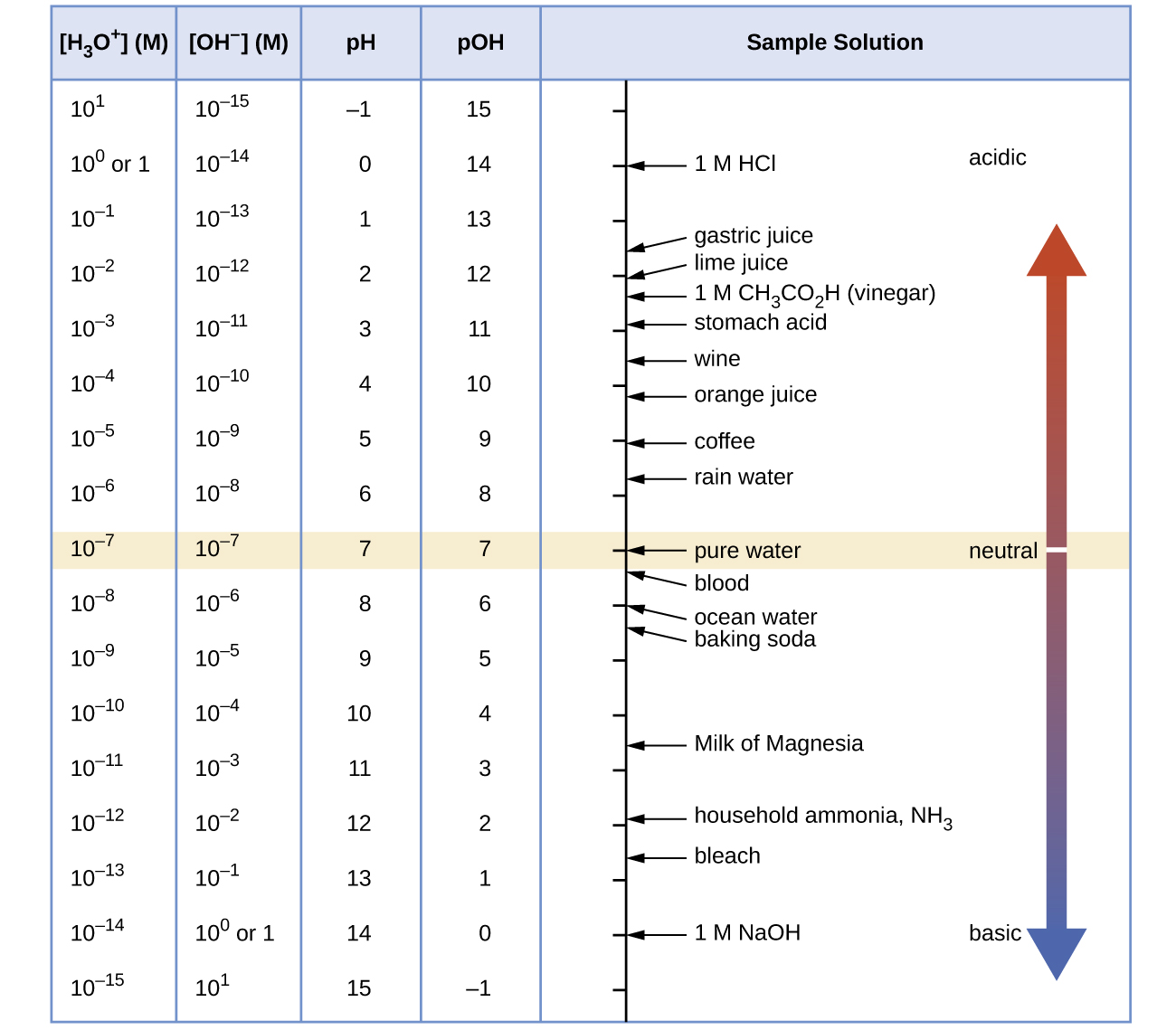
Figure 16.4a shows the relationships between [H3O+], [OH−], pH, and pOH, and gives values for these properties at standard temperatures for some common substances.
Determining pH and pOH from its Reciprocal pH/pOH Value
pOH scale is fairly similar to pH, except instead of measuring the hydrogen ion concentration in moles per litre, it measures the hydroxide ion concentration in moles per litre. As shown earlier in this section (during standard temperature conditions), pH and pOH must add up to 14:
14.00 = pH + pOH
So if you are given pH, you can determine pOH by rearranging the formula:
pOH = 14 – pH
Alternatively, if you are given pOH, you can determine pH by rearranging the formula:
pH = 14 – pOH
Example 16.4a
A cleaning solution has a pOH of 2.5. Calculate the pH of this solution and determine whether this solution is acidic, basic, or neutral.
Solution
Given information
pOH = 2.5
To find the pH, use the formula
pH = 14 – pOH
Solve:
pH = 14 – 2.5
pH = 11.5; this cleaning solution is basic since its pH is greater than 7.
Exercise 16.4b
Exercise 16.4b Part 1:
For each solution listed below, calculate its pOH and determine whether this solution is acidic, basic, or neutral.
- Solution that has a pH = 9.25
- Solution that has a pH = 3.8
Exercise 16.4b Part 2:
For each solution listed below, calculate its pH and determine whether this solution is acidic, basic, or neutral.
- Solution that has a pOH = 5.65
- Solution that has a pOH = 13.1
Check Your Answer[2]
Essentially, the scale for pOH is the reverse of the pH scale.
Source: “Determining pH and pOH from its Reciprocal pH/pOH Value” by Jackie MacDonald, CC-BY-NC-SA 4.0
The acidity of a solution is typically assessed experimentally by measurement of its pH. The pOH of a solution is not usually measured, as it is easily calculated from an experimentally determined pH value. The pH of a solution can be directly measured using a pH meter (Figure 16.4b).

The pH of a solution may also be visually estimated using coloured indicators (Figure 16.4c).

Calculating pH when given Hydronium Concentration
Example 16.4b
Calculation of pH from [H3O+]
What is the pH of stomach acid, a solution of HCl with a hydronium ion concentration of 1.2 × 10−3M?
Solution
[latex]\begin{array}{r @{{}={}} l}\text{pH} & = -\text{log[H}_3\text{O}^{+}]\\[0.5em] & = -\text{log}(1.2\;\times\;10^{-3})\\[0.5em] & = -(-2.92)\\[0.5em] & = 2.92\end{array}[/latex]
(The use of logarithms is explained in Appendix B – The Use of Logarithms and Exponential Numbers Section).
Recall that, as we have done here, when taking the log of a value, keep as many decimal places in the result as there are significant figures in the value. To review significant figures for logarithm calculations, Watch Significant Figures and Logarithms (2min 0s).
Video Source: Study Force (2019, July 22). Significant figures and logarithms [Video]. YouTube.
Exercise 16.4c
Water exposed to air contains carbonic acid, H2CO3, due to the reaction between carbon dioxide and water:
Air-saturated water has a hydronium ion concentration caused by the dissolved CO2 of 2.0 × 10−6M, about 20-times larger than that of pure water. Calculate the pH of the solution at 25 °C.
Check Your Answer[3]
Calculating Hydronium Concentration when given the pH
Example 16.4c
Calculation of Hydronium Ion Concentration from pH
Calculate the hydronium ion concentration of blood that has a pH of 7.3 (slightly alkaline).
Solution
Use the formula:
[latex][\text{H}_3\text{O}^{+}] = 10^{-\text{pH}}[/latex]
Solve given that the pH = 7.3
[H3O+] = 10-7.3
[H3O+] = 5 x 10-8 M
Therefore, the hydronium ion concentration of blood with a pH of 7.3 is 5 x 10-8 M
Source: “Example 16.4c” by Jackie MacDonald, CC-BY-NC-SA 4.0
Exercise 16.4d
Calculate the hydronium ion concentration of a solution with a pH of −1.07.
Check Your Answer[4]
Source: “Exercise 16.4d” by Jackie MacDonald, CC-BY-NC-SA 4.0
Calculating pOH when given Hydroxide Concentration
When you are given a solution’s hydronium concentration, its pH can be calculated using the formula:
[latex]\text{pOH} = -\text{log[OH}^{-}][/latex]
Example 16.4d
What are the pOH and the pH of a 0.0125 M solution of potassium hydroxide, KOH?
Solution
Potassium hydroxide is a highly soluble ionic compound and completely dissociates when dissolved in dilute solution, yielding [OH−] = 0.0125 M:
The pH can be found from the pOH:
Exercise 16.4e
The hydroxide concentration of a sodium hydroxide solution is 0.091 M. Determine the pOH and pH of the solution.
Check Your Answer[5]
Calculating Hydroxide Concentration when given the pOH
When you are given a solution’s hydronium concentration, its pH can be calculated using the formula:
[latex][\text{OH}^{-}] = 10^{-\text{pOH}}[/latex]
Example 16.4e
Calculation of [OH–]
The pOH of house hold bleach is 1.45. What is the [OH–] of this solution?
Solution
Use the formula [OH–] = 10-pOH to determine the hydroxide concentration of the bleach solution.
[OH–] = 10-pOH
[OH–] = 10-1.45
[OH–] = 0.035 M or 3.5 x 10-2 M
Source: “Example 16.4e” by Jackie MacDonald, CC-BY-NC-SA 4.0
Exercise 16.4f
The pOH of toilet a bowl cleaner is measured to be 12.35. What is the [OH–] of this solution? Is this solution acidic or basic?
Check Your Answer[6]
Source: “Exercise 16.5f” by Jackie MacDonald, CC-BY-NC-SA 4.0
Acid/Base Calculations involving Two Steps
Figure 16.4d below shows all of the calculation interrelationships between [H3O+], [OH−], pH, and pOH. The flow chart can be referenced to support students in determining which formula(s) need to be used to solve a given problem.
![This flow chart diagram illustrates the various calculations/interrelationships between [H3O+], [OH−], pH, and pOH. 1. To find pH when given pOH use: pH = 14 - pOH. 2. To find pOH when given pH use: pOH = 14 - pH 3. To find pH when given [H3O+] use: pH = -log[H3O+] 4. To find pOH when given [OH-] use: pOH = -log[OH-] 5. To find [H3O+] when given pH use: [H3O+] = 10^-pH. 6. To find [OH-] when given pOH use: [OH-] = 10^-pOH. 7. To find [H3O+] when given [OH-] use: [H3O+] = 1.0x10^-14 / [OH-] 8. To find [OH-] when given [H3O+] use: [OH-] = 1.0x10^-14 / [H3O+]](https://ecampusontario.pressbooks.pub/app/uploads/sites/3164/2022/12/Figure-16.4b-Calculation-Relationships-between-Hydrogen-Ion-Concentration-Hydroxide-Concentration-pH-and-pOH-scaled-e1673983050469.jpg)
Example 16.4f
Acidic soils typically yield blue or lavender-blue hydrangea blooms. Alkaline (basic) soil tends to grow pinkish-red blooms. If soil has a [OH–] of 6.3 x 10-7 M, what is pH of the soil and what colour blooms will this soil promote for hydrangeas growing in this soil?
Solution:
Given information: [OH–] = 6.3 x 10-7 M
Asked to find: the pH of soil and, thus, the likely colour of the flower’s blooms
Steps – First find pOH, then calculate pH. If acidic, blooms will be blue; if alkaline, blooms will be pink/red.
Step 1 – Calculate pOH using pOH = -log[OH–]
pOH = -log[6.3 x 10-7]
pOH = 6.20
Step 2 – Find the pH and determine colour of the blooms
pH = 14 – pOH
pH = 14 – 6.20
pH = 7.80
Therefore the pH of the soil is 7.80, which is slightly alkaline, so the blooms will be a pinkish/red colour.
Source: “Example 16.4e” by Jackie MacDonald, CC BY-NC-SA 4.0
Exercise 16.4g
The hydronium ion concentration of vinegar is approximately 4 × 10−3M. What is the pOH of this solution?
Check Your Answer[7]
Source: “Exercise 16.4g” by Jackie MacDonald, CC-BY-NC-SA 4.0
Links to Interactive Learning Tools
Explore pH and pOH from the Physics Classroom.
Attribution & References
Except where otherwise noted, this page is adapted by Jackie MacDonald from:
- “14.2 pH and pOH” In Chemistry 2e (Open Stax) by Paul Flowers, Klaus Theopold, Richard Langley & William R. Robinson is licensed under CC BY 4.0. Access for free at Chemistry 2e (Open Stax).
- “14.2 pH and pOH” In General Chemistry 1 & 2 by Rice University, a derivative of Chemistry (Open Stax) by Paul Flowers, Klaus Theopold, Richard Langley & William R. Robinson and is licensed under CC BY 4.0. Access for free at Chemistry (OpenStax) Adaptions and modifications were made to content by Jackie MacDonald for student comprehension
- (1) Basic; (2) Acidic; (3) Basic; (4) Neutral; (5) Acidic; (6) Basic ↵
- Part 1 (a) pOH = 4.75, basic; (b) pOH = 10.2, acidic; Part 2 (a) pH = 8.35, basic; (b) pH = 0.9, acidic ↵
- pH = 5.70 ↵
- [H3O+] = 12 M ↵
- Step 1: Find pOH using [latex]\text{pOH} = -\text{log[OH}^{-}][/latex]; therefore, pOH = 1.04; pH = 14 - 1.04 = 12.96 ↵
- Use the formula [OH-] = 10-pOH to determine the hydroxide concentration of the bleach solution. [OH-] = 10-pOH [OH-] = 10-12.35 [OH-] = 4.5 x 10-13 M; since the pOH is higher than 7, this means its corresponding pH is below 7, and the solution is acidic. ↵
- Step 1: Find pH first using pH = -log[H3O+]; pH = 2.4; Step 2 calculate pOH: pOH = 14 - pH = 14 - 2.4 = 11.6 ↵
The solution in which the concentration of hydroxide ions equals the concentration of hydrogen ions [H3O+] = [OH−]
describes a solution in which [H3O+] > [OH−]
describes a solution in which [H3O+] < [OH−]
The pH scale measures how acidic an object is.
logarithmic measure of the concentration of hydronium ions in a solution
logarithmic measure of the concentration of hydroxide ions in a solution

