7.4 Determining Empirical and Molecular Formulas

Determination of Empirical Formulas

As previously mentioned, the most common approach to determining a compound’s chemical formula is to first measure the masses of its constituent elements. However, we must keep in mind that chemical formulas represent the relative numbers, not masses, of atoms in the substance. Therefore, any experimentally derived data involving mass must be used to derive the corresponding numbers of atoms in the compound. To accomplish this, we can use molar masses to convert the mass of each element to a number of moles. We then consider the moles of each element relative to each other, converting these numbers into a whole-number ratio that can be used to derive the empirical formula of the substance. Consider a sample of compound determined to contain 1.71 g C and 0.287 g H. The corresponding numbers of atoms (in moles) are:

Thus, we can accurately represent this compound with the formula C_0.142H_0.248. Of course, per accepted convention, formulas contain whole-number subscripts, which can be achieved by dividing each subscript by the smaller subscript:

(Recall that subscripts of “1” are not written but rather assumed if no other number is present.)

The empirical formula for this compound is thus CH₂. This may or not be the compound’s molecular formula as well; however, we would need additional information to make that determination (as discussed later in this section).

A molecular formula is the true formula for a compound.  It lists how many atoms of each element are in the compound.  The empirical formula is the simplest or most reduced ratio of elements in a compound. If a compound’s chemical formula cannot be reduced any further, then the empirical formula is the same as the molecular formula.  

Consider as another example a sample of compound determined to contain 5.31 g Cl and 8.40 g O. Following the same approach yields a tentative empirical formula of:

In this case, dividing by the smallest subscript still leaves us with a decimal subscript in the empirical formula. To convert this into a whole number, we must multiply each of the subscripts by two, retaining the same atom ratio and yielding Cl₂O₇ as the final empirical formula.

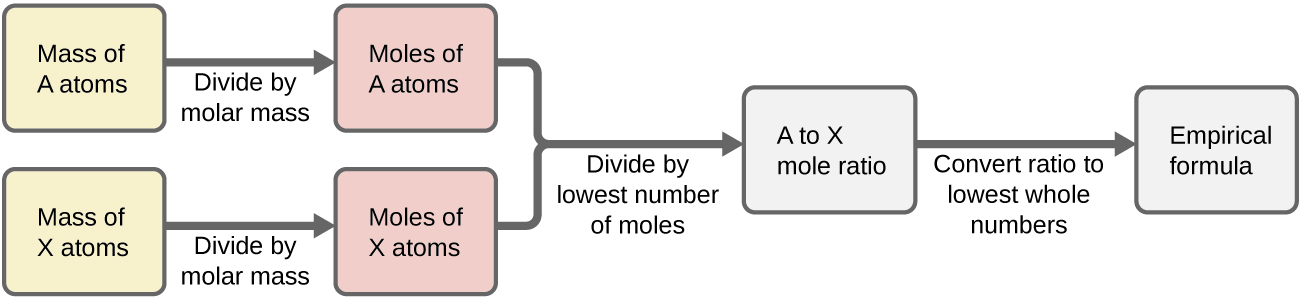
In summary, empirical formulas are derived from experimentally measured element masses by:

1. Deriving the number of moles of each element from its mass
2. Dividing each element’s molar amount by the smallest molar amount to yield subscripts for a tentative empirical formula
3. Multiplying all coefficients by an integer, if necessary, to ensure that the smallest whole-number ratio of subscripts is obtained

Figure 7.4a outlines this procedure in flow chart fashion for a substance containing elements A and X.

Example 7.4a

Determining a Compound’s Empirical Formula from the Masses of Its Elements

A sample of the black mineral hematite (Figure 7.3b), an oxide of iron found in many iron ores, contains 34.97 g of iron and 15.03 g of oxygen. What is the empirical formula of hematite?

Solution

For this problem, we are given the mass in grams of each element. Begin by finding the moles of each:

[latex]\begin{array}{r @{{}={}} l} 34.97 \;\text{g Fe} (\frac{\text{mol Fe}}{55.85 \;\text{g}}) =& 0.6261 \;\text{mol Fe} \\[1em] 15.03 \;\text{g O} (\frac{\text{mol O}}{16.00 \;\text{g}}) =& 0.9394 \;\text{mol O} \end{array}[/latex]

Next, derive the iron-to-oxygen molar ratio by dividing by the lesser number of moles:

[latex]\begin{array}{r @{{}={}} l} \frac{0.6261}{0.6261} =& 1.000 \;\text{mol Fe} \\[1em] \frac{0.9394}{0.6261} =& 1.500 \;\text{mol O} \end{array}[/latex]

The ratio is 1.000 mol of iron to 1.500 mol of oxygen (Fe₁O_1.5). Finally, multiply the ratio by two to get the smallest possible whole number subscripts while still maintaining the correct iron-to-oxygen ratio:

[latex]2(\text{Fe}_1\text{O}_{1.5}) = \text{Fe}_2\text{O}_3[/latex]

The empirical formula is Fe₂O₃.

Watch Calculating Percent Composition and Empirical Formulas

Deriving Empirical Formulas from Percent Composition

Finally, with regard to deriving empirical formulas, consider instances in which a compound’s percent composition is available rather than the absolute masses of the compound’s constituent elements. In such cases, the percent composition can be used to calculate the masses of elements present in any convenient mass of compound; these masses can then be used to derive the empirical formula in the usual fashion.

Example 7.4b

Determining an Empirical Formula from Percent Composition

The bacterial fermentation of grain to produce ethanol forms a gas with a percent composition of 27.29% C and 72.71% O (Figure 7.3c). What is the empirical formula for this gas?

Solution

Since the scale for percentages is 100, it is most convenient to calculate the mass of elements present in a sample weighing 100 g. The calculation is “most convenient” because, per the definition for percent composition, the mass of a given element in grams is numerically equivalent to the element’s mass percentage. This numerical equivalence results from the definition of the “percentage” unit, whose name is derived from the Latin phrase per centum meaning “by the hundred.” Considering this definition, the mass percentages provided may be more conveniently expressed as fractions:

[latex]\begin{array}{r @{{}={}} l} 27.29\% \;\text{C} =& \frac{27.29 \;\text{g C}}{100 \;\text{g compound}} \\[1em] 72.71\% \;\text{O} =& \frac{72.71 \;\text{g O}}{100 \;\text{g compound}} \end{array}[/latex]

The molar amounts of carbon and hydrogen in a 100-g sample are calculated by dividing each element’s mass by its molar mass:

[latex]\begin{array}{r @{{}={}} l} 27.29\% \;\text{C} (\frac{\text{mol C}}{12.01 \;\text{g}}) =& 2.272 \;\text{mol C} \\[1em] 72.71\% \;\text{O} (\frac{\text{mol O}}{16.00 \;\text{g}}) =& 4.544 \;\text{mol O} \end{array}[/latex]

Coefficients for the tentative empirical formula are derived by dividing each molar amount by the lesser of the two:

[latex]\begin{array}{r @{{}={}} l} \frac{2.272 \;\text{g C}}{2.272} =& 1 \\[1em] \frac{4.544 \;\text{g O}}{2.272} & =2 \end{array}[/latex]

Since the resulting ratio is one carbon to two oxygen atoms, the empirical formula is CO₂.

Exercise 7.4b

What is the empirical formula of a compound containing 40.0% C, 6.71% H, and 53.28% O?

Check Your Answer^[2]

Derivation of Molecular Formulas

Recall that empirical formulas are symbols representing the relative numbers of a compound’s elements. Determining the absolute numbers of atoms that compose a single molecule of a covalent compound requires knowledge of both its empirical formula and its molecular mass or molar mass. These quantities may be determined experimentally by various measurement techniques. Molecular mass, for example, is often derived from the mass spectrum of the compound (see discussion of this technique in the previous chapter on atoms and molecules). Molar mass can be measured by a number of experimental methods, many of which will be introduced in later chapters of this text.

Molecular formulas are derived by comparing the compound’s molecular or molar mass to its empirical formula mass. As the name suggests, an empirical formula mass is the sum of the average atomic masses of all the atoms represented in an empirical formula. If we know the molecular (or molar) mass of the substance, we can divide this by the empirical formula mass in order to identify the number of empirical formula units per molecule, which we designate as n:

The molecular formula is then obtained by multiplying each subscript in the empirical formula by n, as shown by the generic empirical formula A_xB_y:

For example, consider a covalent compound whose empirical formula is determined to be CH₂O. The empirical formula mass for this compound is approximately 30 amu (the sum of 12 amu for one C atom, 2 amu for two H atoms, and 16 amu for one O atom). If the compound’s molecular mass is determined to be 180 amu, this indicates that molecules of this compound contain six times the number of atoms represented in the empirical formula:

Molecules of this compound are then represented by molecular formulas whose subscripts are six times greater than those in the empirical formula:

Note that this same approach may be used when the molar mass (g/mol) instead of the molecular mass (amu) is used. In this case, we are merely considering one mole of empirical formula units and molecules, as opposed to single units and molecules.