17.3 Equilibrium Constants

Learning Objectives

By the end of this section, you will be able to:
  • Derive reaction quotients from chemical equations representing homogeneous and heterogeneous reactions
  • Calculate values of reaction quotients and equilibrium constants, using concentrations and pressures
  • Relate the magnitude of an equilibrium constant to properties of the chemical system

Now that we have a symbol (⇌) to designate reversible reactions, we will need a way to express mathematically how the amounts of reactants and products affect the equilibrium of the system. A general equation for a reversible reaction may be written as follows:

[latex]m\text{A}\;+\;n\text{B}\;{\rightleftharpoons}\;x\text{C}\;+\;y\text{D}[/latex]

We can write the reaction quotient (Q) for this equation. When evaluated using concentrations, it is called Qc. We use brackets to indicate molar concentrations of reactants and products.

[latex]Q_c = \frac{[\text{C}]^x[\text{D}]^y}{[\text{A}]^m[\text{B}]^n}[/latex]

The reaction quotient is equal to the molar concentrations of the products of the chemical equation (multiplied together) over the reactants (also multiplied together), with each concentration raised to the power of the coefficient of that substance in the balanced chemical equation. For example, the reaction quotient for the reversible reaction [latex]2\text{ NO}_2(g)\;{\rightleftharpoons}\;\text{N}_2\text{O}_4(g)[/latex] is given by this expression:

 

[latex]Q_c = \frac{[\text{N}_2\text{O}_4]}{[\text{NO}_2]^2}[/latex]

Example 17.3a

Writing Reaction Quotient Expressions

Write the expression for the reaction quotient for each of the following reactions:

  1. [latex]3\text{ O}_2(g)\;{\rightleftharpoons}\;2\text{ O}_3(g)[/latex]
  2. [latex]\text{N}_2(g)\;+\;3\text{ H}_2(g)\;{\rightleftharpoons}\;2\text{ NH}_3(g)[/latex]
  3. [latex]4\text{ NH}_3(g)\;+\;7\text{ O}_2(g)\;{\rightleftharpoons}\;4\text{ NO}_2(g)\;+\;6\text{ H}_2\text{O}(g)[/latex]

Solution

  1. [latex]Q_c = \frac{[\text{O}_3]^2}{[\text{O}_2]^3}[/latex]
  2. [latex]Q_c = \frac{[\text{NH}_3]^2}{[\text{N}_2][\text{H}_2]^3}[/latex]
  3. [latex]Q_c = \frac{[\text{NO}_2]^4[\text{H}_2\text{O}]^6}{[\text{NH}_3]^4[\text{O}_2]^7}[/latex]

Exercise 17.3a

Write the expression for the reaction quotient for each of the following reactions:

  1. [latex]2\text{ SO}_2(g)\;+\;\text{O}_2(g)\;{\rightleftharpoons}\;2\text{ SO}_3(g)[/latex]
  2. [latex]\text{C}_4\text{H}_8(g)\;{\rightleftharpoons}\;2\text{ C}_2\text{H}_4(g)[/latex]
  3. [latex]2\text{ C}_4\text{H}_{10}(g)\;+\;13\text{ O}_2(g)\;{\rightleftharpoons}\;8\text{ CO}_2(g)\;+\;10\text{ H}_2\text{O}(g)[/latex]

Check Your Answer[1]

The numeric value of Qc for a given reaction varies; it depends on the concentrations of products and reactants present at the time when Qc is determined. When pure reactants are mixed, Qc is initially zero because there are no products present at that point. As the reaction proceeds, the value of Qc increases as the concentrations of the products increase and the concentrations of the reactants simultaneously decrease (Figure 17.3a). When the reaction reaches equilibrium, the value of the reaction quotient no longer changes because the concentrations no longer change.

Three graphs are shown and labeled, “a,” “b,” and “c.” All three graphs have a vertical dotted line running through the middle labeled, “Equilibrium is reached.” The y-axis on graph a is labeled, “Concentration,” and the x-axis is labeled, “Time.” Three curves are plotted on graph a. The first is labeled, “[ S O subscript 2 ];” this line starts high on the y-axis, ends midway down the y-axis, has a steep initial slope and a more gradual slope as it approaches the far right on the x-axis. The second curve on this graph is labeled, “[ O subscript 2 ];” this line mimics the first except that it starts and ends about fifty percent lower on the y-axis. The third curve is the inverse of the first in shape and is labeled, “[ S O subscript 3 ].” The y-axis on graph b is labeled, “Concentration,” and the x-axis is labeled, “Time.” Three curves are plotted on graph b. The first is labeled, “[ S O subscript 2 ];” this line starts low on the y-axis, ends midway up the y-axis, has a steep initial slope and a more gradual slope as it approaches the far right on the x-axis. The second curve on this graph is labeled, “[ O subscript 2 ];” this line mimics the first except that it ends about fifty percent lower on the y-axis. The third curve is the inverse of the first in shape and is labeled, “[ S O subscript 3 ].” The y-axis on graph c is labeled, “Reaction Quotient,” and the x-axis is labeled, “Time.” A single curve is plotted on graph c. This curve begins at the bottom of the y-axis and rises steeply up near the top of the y-axis, then levels off into a horizontal line. The top point of this line is labeled, “k.”
Figure 17.3a: (a) The change in the concentrations of reactants and products is depicted as the 2 SO2(g) + O2(g) ⇌ 2 SO3(g) reaction approaches equilibrium. (b) The change in concentrations of reactants and products is depicted as the reaction 2 SO3(g) ⇌ 2 SO2(g) + O2(g) approaches equilibrium. (c) The graph shows the change in the value of the reaction quotient as the reaction approaches equilibrium (credit: Chemistry (OpenStax), CC BY 4.0).

When a mixture of reactants and products of a reaction reaches equilibrium at a given temperature, its reaction quotient always has the same value. This value is called the equilibrium constant (K)  of the reaction at that temperature. As for the reaction quotient, when evaluated in terms of concentrations, it is noted as Kc.

That a reaction quotient always assumes the same value at equilibrium can be expressed as:

[latex]Q_c\;\text{at equilibrium} = K_c = \frac{[\text{C}]^x[\text{D}]^y{\dots}}{[\text{A}]^m[\text{B}]^n{\dots}}[/latex]

This equation is a mathematical statement of the law of mass action: When a reaction has attained equilibrium at a given temperature, the reaction quotient for the reaction always has the same value.

Example 17.3b

Evaluating a Reaction Quotient

Gaseous nitrogen dioxide forms dinitrogen tetroxide according to this equation:

[latex]2\text{ NO}_2(g)\;{\rightleftharpoons}\;\text{N}_2\text{O}_4(g)[/latex]

When 0.10 mol NO2 is added to a 1.0-L flask at 25 °C, the concentration changes so that at equilibrium, [NO2] = 0.016 M and [N2O4] = 0.042 M.

  1. What is the value of the reaction quotient before any reaction occurs?
  2. What is the value of the equilibrium constant for the reaction?

Solution

  1. Before any product is formed, [latex][\text{NO}_2] = \frac{0.10\;\text{mol}}{1.0\;\text{L}} = 0.10\;M[/latex], and [N2O4] = 0 M. Thus,
    [latex]Q_c = \frac{[\text{N}_2\text{O}_4]}{[\text{NO}_2]^2} = \frac{0}{0.10^2} = 0[/latex]
  2. At equilibrium, the value of the equilibrium constant is equal to the value of the reaction quotient. At equilibrium,
    [latex]K_c = Q_c = \frac{[\text{N}_2\text{O}_4]}{[\text{NO}_2]^{2}} = \frac{0.042}{0.016^2} = 1.6\;\times\;10^{2}[/latex].
    The equilibrium constant is 1.6 × 102.

Note that dimensional analysis would suggest the unit for this Kc value should be M−1. However, it is common practice to omit units for Kc values computed as described here, since it is the magnitude of an equilibrium constant that relays useful information. As will be discussed later in this module, the rigorous approach to computing equilibrium constants uses dimensionless quantities derived from concentrations instead of actual concentrations, and so Kc values are truly unitless.

Exercise 17.3b

Check Your Learning Exercise (Text Version)

For the reaction, 2 SO2(g) + O2(g) ↔ 2 SO3(g) the concentrations at equilibrium are [SO2] = 0.90 M, [O2] = 0.35 M, and [SO3] = 1.1 M. What is the value of the equilibrium constant, Kc?

    1. 1.1
    2. 4.3
    3. 8.6
    4. 0.90

Check Your Answer[2]

Source: “Exercise 17.3b” is adapted from “Example 13.2-2” in General Chemistry 1 & 2, a derivative of Chemistry (Open Stax) by Paul Flowers, Klaus Theopold, Richard Langley & William R. Robinson, licensed under CC BY 4.0.

The magnitude of an equilibrium constant is a measure of the yield of a reaction when it reaches equilibrium. A large value for Kc indicates that equilibrium is attained only after the reactants have been largely converted into products. A small value of Kc – much less than 1 – indicates that equilibrium is attained when only a small proportion of the reactants have been converted into products.

Once a value of Kc is known for a reaction, it can be used to predict directional shifts when compared to the value of Qc. A system that is not at equilibrium will proceed in the direction that establishes equilibrium. The data in Figure 17.3b illustrate this. When heated to a consistent temperature, 800 °C, different starting mixtures of CO, H2O, CO2, and H2 react to reach compositions adhering to the same equilibrium (the value of Qc changes until it equals the value of Kc). This value is 0.640, the equilibrium constant for the reaction under these conditions.

[latex]\text{CO}(g)\;+\;\text{H}_2\text{O}(g)\;{\rightleftharpoons}\;\text{CO}_2(g)\;+\;\text{H}_2(g)\;\;\;\;\;\;\;K_c = 0.640\;\;\;\;\;\;\;\text{T} = 800\;^{\circ}\text{C}[/latex]

It is important to recognize that an equilibrium can be established starting either from reactants or from products, or from a mixture of both. For example, equilibrium was established from Mixture 2 in Figure 17.3b when the products of the reaction were heated in a closed container. In fact, one technique used to determine whether a reaction is truly at equilibrium is to approach equilibrium starting with reactants in one experiment and starting with products in another. If the same value of the reaction quotient is observed when the concentrations stop changing in both experiments, then we may be certain that the system has reached equilibrium.

 

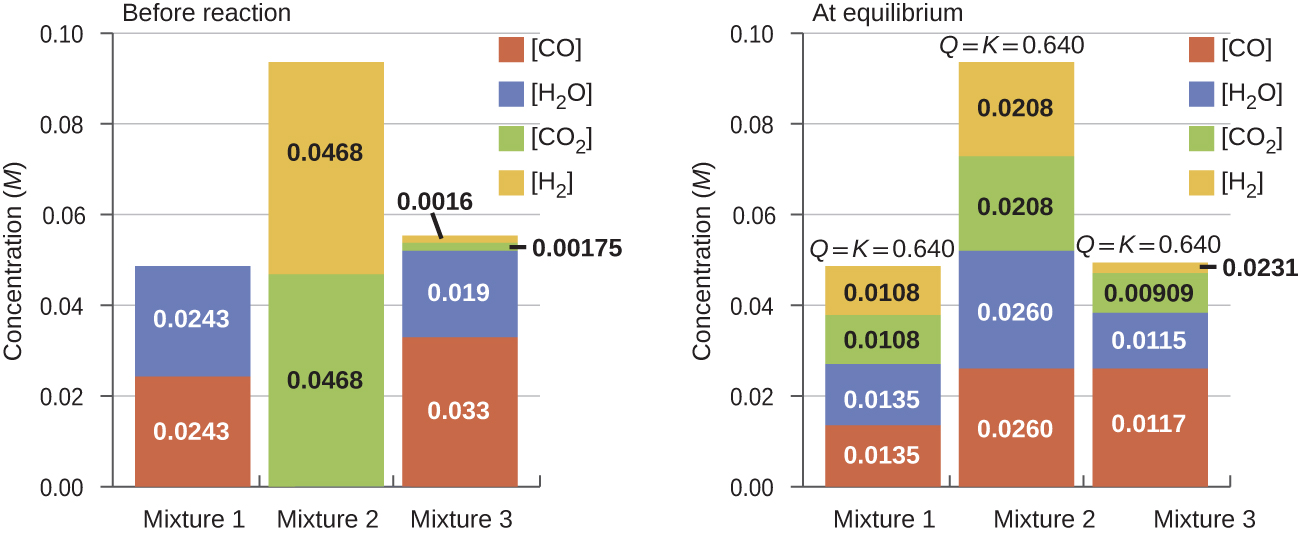
Two sets of bar graphs are shown. The left is labeled, “Before reaction,” and the right is labeled, “At equilibrium.” Both graphs have y-axes labeled, “Concentration ( M ),” and three bars on the x-axes labeled, “Mixture 1,” “Mixture 2,” and “Mixture 3.” The y-axis has a scale beginning at 0.00 and ending at 0.10, with measurement increments of 0.02. The bars on the graphs are color coded and a key is provided with a legend. Red is labeled, “C O;” blue is labeled, “H subscript 2 O;” green is labeled, “C O subscript 2,” and yellow is labeled, “H subscript 2.” The graph on the left shows the red bar for mixture one just above 0.02 and the blue bar near 0.05. For mixture two, the green bar is near 0.05, and the yellow bar is near 0.09. For mixture 3, the red bar is near 0.01, the blue bar is slightly above that with green and yellow topping it off at 0.02. On the right graph, the bar for mixture one shows the red bar slightly above 0.01, the blue bar stacked on it rising slightly above 0.02, the green rising near 0.04, and the yellow bar reaching near 0.05. A label above this bar reads, “Q equals 0.640.” The bar for mixture two shows the red bar slightly above 0.02, the blue bar stacked on it rising near 0.05, the green rising near 0.07, and the yellow bar reaching near 0.10. A label above this bar reads “Q equals 0.640.” The bar for mixture three shows the red bar near 0.01, the blue bar stacked on it rising slightly above 0.01, the green rising near 0.02, and the yellow bar reaching 0.02. A label above this bar reads “Q equals 0.640”.
Figure 17.3b: Concentrations of three mixtures are shown before and after reaching equilibrium at 800 °C for the so-called water gas shift reaction: CO(g) + H2O(g) ⇌ CO2(g) + H2(g) (credit: Chemistry (OpenStax), CC BY 4.0).

Example 17.3c

Predicting the Direction of Reaction

Given here are the starting concentrations of reactants and products for three experiments involving this reaction:

[latex]\text{CO}(g)\;+\;\text{H}_2\text{O}(g)\;{\rightleftharpoons}\;\text{CO}_2(g)\;+\;\text{H}_2(g)[/latex]
[latex]K_c = 0.64[/latex]

Determine in which direction the reaction proceeds as it goes to equilibrium in each of the three experiments shown.

Reactants/Products Experiment 1 Experiment 2 Experiment 3
[CO]i 0.0203 M 0.011 M 0.0094 M
[H2O]i 0.0203 M 0.0011 M 0.0025 M
[CO2]i 0.0040 M 0.037 M 0.0015 M
[H2]i 0.0040 M 0.046 M 0.0076 M

Solution

Experiment 1:

[latex]Q_c = \frac{[\text{CO}_2][\text{H}_2]}{[\text{CO}][\text{H}_2\text{O}]} = \frac{(0.0040)(0.0040)}{(0.0203)(0.0203)} = 0.039[/latex].

Qc < Kc (0.039 < 0.64)

The reaction will shift to the right.

Experiment 2:

[latex]Q_c = \frac{[\text{CO}_2][\text{H}_2]}{[\text{CO}][\text{H}_2\text{O}]} = \frac{(0.037)(0.046)}{(0.011)(0.0011)} = 1.4\;\times\;10^2[/latex]

Qc > Kc (140 > 0.64)

The reaction will shift to the left.

Experiment 3:

[latex]Q_c = \frac{[\text{CO}_2][\text{H}_2]}{[\text{CO}][\text{H}_2\text{O}]} = \frac{(0.0015)(0.0076)}{(0.0094)(0.0025)} = 0.48[/latex]

Qc < Kc (0.48 < 0.64)

The reaction will shift to the right.

Exercise 17.3c

Calculate the reaction quotient and determine the direction in which each of the following reactions will proceed to reach equilibrium.

  1. A 1.00-L flask containing 0.0500 mol of NO(g), 0.0155 mol of Cl2(g), and 0.500 mol of NOCl:
    [latex]2\text{ NO}(g)\;+\;\text{Cl}_2(g)\;{\rightleftharpoons}\;2\text{ NOCl}(g)\;\;\;\;\;\;\;K_c = 4.6\;\times\;10^4[/latex]
  2. A 5.0-L flask containing 17 g of NH3, 14 g of N2, and 12 g of H2:
    [latex]\text{N}_2(g)\;+\;3\text{ H}_2(g)\;{\rightleftharpoons}\;2\text{ NH}_3(g)\;\;\;\;\;\;\;K_c = 0.060[/latex]
  3. A 2.00-L flask containing 230 g of SO3(g):
    [latex]2\text{ SO}_3(g)\;{\rightleftharpoons}\;2\text{ SO}_2(g)\;+\;\text{O}_2(g)\;\;\;\;\;\;\;K_c = 0.230[/latex]

Check Your Answer[3]

In Example 17.3c, it was mentioned that the common practice is to omit units when evaluating reaction quotients and equilibrium constants. It should be pointed out that using concentrations in these computations is a convenient but simplified approach that sometimes leads to results that seemingly conflict with the law of mass action. For example, equilibria involving aqueous ions often exhibit equilibrium constants that vary quite significantly (are not constant) at high solution concentrations. This may be avoided by computing Kc values using the activities of the reactants and products in the equilibrium system instead of their concentrations. The activity of a substance is a measure of its effective concentration under specified conditions. While a detailed discussion of this important quantity is beyond the scope of an introductory text, it is necessary to be aware of a few important aspects:

  • Activities are dimensionless (unitless) quantities and are in essence “adjusted” concentrations.
  • For relatively dilute solutions, a substance’s activity and its molar concentration are roughly equal.
  • Activities for pure condensed phases (solids and liquids) are equal to 1.

As a consequence of this last consideration, Qc and Kc expressions do not contain terms for solids or liquids (being numerically equal to 1, these terms have no effect on the expression’s value). Several examples of equilibria yielding such expressions will be encountered in this section.

Homogeneous Equilibria

A homogeneous equilibrium is one in which all of the reactants and products are present in a single solution (by definition, a homogeneous mixture). In this chapter, we will concentrate on the two most common types of homogeneous equilibria: those occurring in liquid-phase solutions and those involving exclusively gaseous species. Reactions between solutes in liquid solutions belong to one type of homogeneous equilibria. The chemical species involved can be molecules, ions, or a mixture of both. Several examples are provided here.

[latex]\begin{array}{rll @{{}={}} ll} \text{C}_2\text{H}_2(aq)\;+\;2\text{ Br}_2(aq)\;{\rightleftharpoons}\;\text{C}_2\text{H}_2\text{Br}_4(aq) & K_c & = \frac{[\text{C}_2\text{H}_2\text{Br}_4]}{[\text{C}_2\text{H}_2][\text{Br}_2]^2} \\[0.5em] \text{I}_2(aq)\;+\;\text{I}^{-}(aq)\;{\rightleftharpoons}\;\text{I}_3^{\;\;-}(aq) & K_c & = \frac{[\text{I}_3^{\;\;-}]}{[\text{I}_2][\text{I}^{-}]} \\[0.5em] \text{Hg}_2^{\;\;2+}(aq)\;+\;\text{NO}_3^{\;\;-}(aq)\;+\;3\text{ H}_3\text{O}^{+}(aq) \\[0.5em] {\rightleftharpoons}\;2\text{ Hg}^{2+}(aq)\;+\;\text{HNO}_2(aq)\;+\;4\text{ H}_2\text{O}(l) & K_c & = \frac{[\text{Hg}^{2+}]^2[\text{HNO}_2]}{[\text{Hg}_2^{\;\;2+}][\text{NO}_3^{\;\;-}][\text{H}_3\text{O}^{+}]^3} \\[0.5em] \text{HF}(aq)\;+\;\text{H}_2\text{O}(l)\;{\rightleftharpoons}\;\text{H}_3\text{O}^{+}(aq)\;+\;\text{F}^{-}(aq) & K_c & = \frac{[\text{H}_3\text{O}^{+}][\text{F}^{-}]}{[\text{HF}]} \\[0.5em] \text{NH}_3(aq)\;+\;\text{H}_2\text{O}(l)\;{\rightleftharpoons}\;\text{NH}_4^{\;\;+}(aq)\;+\;\text{OH}^{-}(aq) & K_c & = \frac{[\text{NH}_4^{\;\;+}][\text{OH}^{-}]}{[\text{NH}_3]} \end{array}[/latex]

In each of these examples, the equilibrium system is an aqueous solution, as denoted by the aq annotations on the solute formulas. Since H2O(l) is the solvent for these solutions, its concentration does not appear as a term in the Kc expression, as discussed earlier, even though it may also appear as a reactant or product in the chemical equation.

Reactions in which all reactants and products are gases represent a second class of homogeneous equilibria. We use molar concentrations in the following examples, but we will see shortly that partial pressures of the gases may be used as well.

[latex]\begin{array}{rlrl @{{}\rightleftharpoons{}} rl} \text{C}_2\text{H}_6(g) & \rightleftharpoons\text{C}_2\text{H}_4(g)\;+\;\text{H}_2(g) & K_c & = \frac{[\text{C}_2\text{H}_4][\text{H}_2]}{[\text{C}_2\text{H}_6]} \\[0.5em] 3\text{ O}_2(g) & \rightleftharpoons 2\text{ O}_3(g) & K_c & = \frac{[\text{O}_3]^2}{[\text{O}_2]^3} \\[0.5em] \text{N}_2(g)\;+\;3\text{ H}_2(g) & \rightleftharpoons 2\text{ NH}_3(g) & K_c & = \frac{[\text{NH}_3]^2}{[\text{N}_2][\text{H}_2]^3} \\[0.5em] \text{C}_3\text{H}_8(g)\;+\;5\text{ O}_2(g) & \rightleftharpoons 3\text{ CO}_2(g)\;+\;4\text{ H}_2\text{O}(g) & K_c & = \frac{[\text{CO}_2]^3[\text{H}_2\text{O}]^4}{[\text{C}_3\text{H}_8][\text{O}_2]^5} \end{array}[/latex]

Note that the concentration of H2O(g) has been included in the last example because water is not the solvent in this gas-phase reaction and its concentration (and activity) changes.

Whenever gases are involved in a reaction, the partial pressure of each gas can be used instead of its concentration in the equation for the reaction quotient because the partial pressure of a gas is directly proportional to its concentration at constant temperature. This relationship can be derived from the ideal gas equation, where M is the molar concentration of gas, [latex]\frac{n}{V}[/latex].

[latex]\begin{array}{r @{{}={}} l} PV & = nRT \\[0.5em] P & = (\frac{n}{V})\;RT \\[0.5em] & = MRT \end{array}[/latex]

Thus, at constant temperature, the pressure of a gas is directly proportional to its concentration.

Using the partial pressures of the gases, we can write the reaction quotient for the system

[latex]\text{C}_2\text{H}_6(g)\;{\rightleftharpoons}\;\text{C}_2\text{H}_4(g)\;+\;\text{H}_2(g)[/latex]

by following the same guidelines for deriving concentration-based expressions:

[latex]Q_P = \frac{P_{\text{C}_2\text{H}_4}P_{\text{H}_2}}{P_{\text{C}_2\text{H}_6}}[/latex]

In this equation we use QP to indicate a reaction quotient written with partial pressures: [latex]P_{\text{C}_2\text{H}_6}[/latex] is the partial pressure of C2H6; [latex]P_{\text{H}_2}[/latex], the partial pressure of H2; and [latex]P_{\text{C}_2\text{H}_6}[/latex], the partial pressure of C2H4. At equilibrium:

[latex]K_P = Q_P = \frac{P_{\text{C}_2\text{H}_4}P_{\text{H}_2}}{P_{\text{C}_2\text{H}_6}}[/latex]

The subscript P in the symbol KP designates an equilibrium constant derived using partial pressures instead of concentrations. The equilibrium constant, KP, is still a constant, but its numeric value may differ from the equilibrium constant found for the same reaction by using concentrations.

Conversion between a value for Kc, an equilibrium constant expressed in terms of concentrations, and a value for KP, an equilibrium constant expressed in terms of pressures, is straightforward (a K or Q without a subscript could be either concentration or pressure).

The equation relating Kc and KP is derived as follows. For the gas-phase reaction [latex]m\text{A}\;+\;n\text{B}\;{\rightleftharpoons}\;x\text{C}\;+\;y\text{D}[/latex]:

[latex]\begin{array}{r @{{}={}} l} K_P & = \frac{(P_C)^x(P_D)^y}{(P_A)^m(P_B)^n} \\[0.5em] & = \frac{([\text{C}]\;\times\;RT)^x([\text{D}]\;\times\;RT)^y}{([\text{A}]\;\times\;RT)^m([\text{B}]\;\times\;RT)^n} \\[0.5em] & = \frac{[\text{C}]^x[\text{D}]^y}{[\text{A}]^m[\text{B}]^n}\;\times\;\frac{(RT)^{x+y}}{(RT)^{m+n}} \\[0.5em] & = K_c(RT)^{(x+y)\;-\;(m+n)} \\[0.5em] & = K_c(RT)^{{\Delta}n} \end{array}[/latex]

The relationship between Kc and KP is

[latex]K_P = K_c(RT)^{{\Delta}n}[/latex]

In this equation, Δn is the difference between the sum of the coefficients of the gaseous products and the sum of the coefficients of the gaseous reactants in the reaction (the change in moles of gas between the reactants and the products). For the gas-phase reaction [latex]m\text{A}\;+\;n\text{B}\;{\leftrightharpoons}\;x\text{C}\;+\;y\text{D}[/latex], we have

[latex]{\Delta}n = (x\;+\;y)\;-\;(m\;+\;n)[/latex]

Example 17.3d

Calculation of KP

Write the equations for the conversion of Kc to KP for each of the following reactions:

  1. [latex]\text{C}_2\text{H}_6(g)\;{\rightleftharpoons}\;\text{C}_2\text{H}_4(g)\;+\;\text{H}_2(g)[/latex]
  2. [latex]\text{CO}(g)\;+\;\text{H}_2\text{O}(g)\;{\rightleftharpoons}\;\text{CO}_2(g)\;+\;\text{H}_2(g)[/latex]
  3. [latex]\text{N}_2(g)\;+\;3\text{ H}_2(g)\;{\rightleftharpoons}\;2\text{ NH}_3(g)[/latex]
  4. Kc is equal to 0.28 for the following reaction at 900 °C:
    [latex]\text{CS}_2(g)\;+\;4\text{ H}_2(g)\;{\rightleftharpoons}\;\text{CH}_4(g)\;+\;2\text{ H}_2\text{S}(g)[/latex]
    What is KP at this temperature?

Solution

  1. Δn = (2) − (1) = 1
    KP = Kc (RT)Δn = Kc (RT)1 = Kc (RT)

  2. Δn = (2) − (2) = 0
    KP = Kc (RT)Δn = Kc (RT)0 = Kc

  3. Δn = (2) − (1 + 3) = −2
    KP = Kc (RT)Δn = Kc (RT)−2 = [latex]\frac{K_c}{(RT)^2}[/latex]

  4. KP = Kc (RT)Δn = (0.28)[(0.0821)(1173)]−2 = 3.0 × 10−5

Exercise 17.3d

Write the equations for the conversion of Kc to KP for each of the following reactions, which occur in the gas phase:

  1. [latex]2\text{ SO}_2(g)\;+\;\text{O}_2(g)\;{\rightleftharpoons}\;2\text{ SO}_3(g)[/latex]
  2. [latex]\text{N}_2\text{O}_4(g)\;{\rightleftharpoons}\;2\text{ NO}_2(g)[/latex]
  3. [latex]\text{C}_3\text{H}_8(g)\;+\;5\text{ O}_2(g)\;{\rightleftharpoons}\;3\text{ CO}_2(g)\;+\;4\text{ H}_2\text{O}(g)[/latex]
  4. At 227 °C, the following reaction has Kc = 0.0952:
    [latex]\text{CH}_3\text{OH}(g)\;{\rightleftharpoons}\;\text{CO}(g)\;+\;2\text{ H}_2(g)[/latex]
    What would be the value of KP at this temperature

Check Your Answer[4]

Heterogeneous Equilibria

A heterogeneous equilibrium is a system in which reactants and products are found in two or more phases. The phases may be any combination of solid, liquid, or gas phases, and solutions. When dealing with these equilibria, remember that solids and pure liquids do not appear in equilibrium constant expressions (the activities of pure solids, pure liquids, and solvents are 1).

Some heterogeneous equilibria involve chemical changes; for example:

[latex]\begin{array}{rl @{{}\rightleftharpoons{}} ll} \text{PbCl}_2(s) & \rightleftharpoons\text{Pb}^{2+}(aq)\;+\;2\text{ Cl}^{-}(aq) & K_c & = [\text{Pb}^{2+}][\text{Cl}^{-}]^2 \\[0.5em] \text{CaO}(s)\;+\;\text{CO}_2(g) & \rightleftharpoons\text{CaCO}_3(s) & K_c & = \frac{1}{[\text{CO}_2]} \\[0.5em] \text{C}(s)\;+\;2\text{ S}(g) & \rightleftharpoons\text{CS}_2(g) & K_c & = \frac{[\text{CS}_2]}{[\text{S}]^2} \end{array}[/latex]

Other heterogeneous equilibria involve phase changes, for example, the evaporation of liquid bromine, as shown in the following equation:

[latex]\text{Br}_2(l)\;{\rightleftharpoons}\;\text{Br}_2(g)\;\;\;\;\;\;\;K_c = [\text{Br}_2][/latex]

We can write equations for reaction quotients of heterogeneous equilibria that involve gases, using partial pressures instead of concentrations. Two examples are:

[latex]\begin{array}{r @{{}\rightleftharpoons{}} ll} \text{CaO}(s)\;+\;\text{CO}_2(g) & \rightleftharpoons\text{CaCO}_3(s) & K_P = \frac{1}{P_{\text{CO}_2}} \\[0.5em] \text{C}(s)\;+\;2\text{ S}(g) & \rightleftharpoons\text{CS}_2(g) & K_P = \frac{P_{\text{CS}_2}}{(P_{\text{S}})^2} \end{array}[/latex]

Links to Interactive Learning Tools

Explore Equilibrium Constant Expression from the Physics Classroom.

Key Equations

  • [latex]Q = \frac{[\text{C}]^x[\text{D}]^y}{[\text{A}]^m[\text{B}]^n}\;\;\;\;\;\;\;\text{where}\;m\text{A}\;+\;n\text{B}\;{\rightleftharpoons}\;x\text{C}\;+\;y\text{D}[/latex]
  • [latex]Q_P = \frac{(P_C)^x(P_D)^y}{(P_A)^m(P_B)^n}\;\;\;\;\;\;\;\text{where}\;m\text{A}\;+\;n\text{B}\;{\rightleftharpoons}\;x\text{C}\;+\;y\text{D}[/latex]
  • P = MRT
  • KP = Kc (RT)Δn

Attribution & References

Except where otherwise noted, this page is adapted by David Wegman from “13.2 Equilibrium Constants” In General Chemistry 1 & 2 by Rice University, a derivative of Chemistry (Open Stax) by Paul Flowers, Klaus Theopold, Richard Langley & William R. Robinson and is licensed under CC BY 4.0. ​Access for free at Chemistry (OpenStax)
  1. (a) [latex]Q_c = \frac{[\text{SO}_3]^2}{[\text{SO}_2]^2[\text{O}_2]}[/latex]; (b) [latex]Q_c = \frac{[\text{C}_2\text{H}_4]^2}{[\text{C}_4\text{H}_8]}[/latex]; (c) [latex]Q_c = \frac{[\text{CO}_2]^8[\text{H}_2\text{O}]^{10}}{[\text{C}_4\text{H}_{10}]^2[\text{O}_2]^{13}}[/latex] ↵
  2. b) 4.3 ↵
  3. (a) Qc = 6.45 × 103, shifts right. (b) Qc = 0.12, shifts left. (c) Qc = 0, shifts right ↵
      1. KP = Kc (RT)−1;
      2. KP = Kc (RT);
      3. KP = Kc (RT);
      4. 160 or 1.6 × 102
    ↵
definition

License

Icon for the Creative Commons Attribution 4.0 International License

Enhanced Introductory College Chemistry Copyright © 2023 by Gregory Anderson; Caryn Fahey; Jackie MacDonald; Adrienne Richards; Samantha Sullivan Sauer; J.R. van Haarlem; and David Wegman is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book