14.3 Molarity

Learning Objectives

By the end of this section, you will be able to:

  • Describe the fundamental properties of solutions
  • Calculate solution concentrations using molarity
  • Perform dilution calculations using the dilution equation

In preceding sections, we focused on the composition of substances: samples of matter that contain only one type of element or compound. However, mixtures—samples of matter containing two or more substances physically combined—are more commonly encountered in nature than are pure substances. Similar to a pure substance, the relative composition of a mixture plays an important role in determining its properties. The relative amount of oxygen in a planet’s atmosphere determines its ability to sustain aerobic life. The relative amounts of iron, carbon, nickel, and other elements in steel (a mixture known as an “alloy”) determine its physical strength and resistance to corrosion. The relative amount of the active ingredient in a medicine determines its effectiveness in achieving the desired pharmacological effect. The relative amount of sugar in a beverage determines its sweetness (see Figure 14.3a). In this section, we will describe one of the most common ways in which the relative compositions of mixtures may be quantified.

A picture is shown of sugar being poured from a spoon into a cup of coffee.
Figure 14.3a: Sugar is one of many components in the complex mixture known as coffee. The amount of sugar in a given amount of coffee is an important determinant of the beverage’s sweetness. (credit: Photo by Jane Whitney in Chemistry (OpenStax), CC BY 4.0).

Solutions

We have previously defined solutions as homogeneous mixtures, meaning that the composition of the mixture (and therefore its properties) is uniform throughout its entire volume. Solutions occur frequently in nature and have also been implemented in many forms of manmade technology. We will explore a more thorough treatment of solution properties in the chapter on colloids, but here we will introduce some of the basic properties of solutions.

The relative amount of a given solution component is known as its concentration. Often, though not always, a solution contains one component with a concentration that is significantly greater than that of all other components. This component is called the solvent and may be viewed as the medium in which the other components are dispersed, or dissolved. Solutions in which water is the solvent are, of course, very common on our planet. A solution in which water is the solvent is called an aqueous solution.

A solute is a component of a solution that is typically present at a much lower concentration than the solvent. Solute concentrations are often described with qualitative terms such as dilute (of relatively low concentration) and concentrated (of relatively high concentration).

Concentrations may be quantitatively assessed using a wide variety of measurement units, each convenient for particular applications. Molarity (M) is a useful concentration unit for many applications in chemistry. Molarity is defined as the number of moles of solute in exactly 1 litre (1 L) of the solution:

[latex]M = \frac{\text{mol solute}}{\text{L solution}}[/latex]

Example 14.3a

Calculating Molarity

A 355-mL soft drink sample contains 0.133 mol of sucrose (table sugar). What is the molar concentration of sucrose in the beverage?

Solution

Since the molar amount of solute and the volume of solution are both given, the molarity can be calculated using the definition of molarity. Per this definition, the solution volume must be converted from mL to L:

[latex]M = \frac{\text{mol solute}}{\text{L solution}} = \frac{0.133 \;\text{mol}}{355 \;\text{mL} \times \frac{1 \;\text{L}}{1000 \;\text{mL}}} = 0.375 \; M[/latex]

Exercise 14.3a

Check Your Learning Exercise (Text Version)

A teaspoon of table sugar contains about 0.01 mol sucrose. What is the molarity of sucrose if a teaspoon of sugar has been dissolved in a cup of tea with a volume of 200 mL?

  1. 0.05 M
  2. 0.03 M
  3. 0.07 M
  4. 0.04 M

Check Your Answer[1]

Source: “Exercise 14.3a” is adapted from “Example 6.3-1” in General Chemistry 1 & 2, a derivative of Chemistry (Open Stax) by Paul Flowers, Klaus Theopold, Richard Langley & William R. Robinson, licensed under CC BY 4.0.

Example 14.3b

Deriving Moles and Volumes from Molarity

How much sugar (mol) is contained in a modest sip (~10 mL) of the soft drink from Example 14.3a?

Solution

In this case, we can rearrange the definition of molarity to isolate the quantity sought, moles of sugar. We then substitute the value for molarity that we derived in Example 14.3a, 0.375 M:

[latex]M = \frac{\text{mol solute}}{\text{L solution}}[/latex]
[latex]\text{mol solute} = M \times \text{L solution}[/latex]

[latex]\text{mol solute} = 0.375 \;\frac{\text{mol sugar}}{\text{L}} \times (10 \;\text{mL} \times \frac{1 \text{L}}{1000 \;\text{mL}}) = 0.004 \;\text{mol sugar}[/latex]

Exercise 14.3b

Check Your Learning Exercise (Text Version)

What volume (mL) of the sweetened tea (0.05M) described in Exercise 14.3a contains the same amount of sugar as 10 mL of the soft drink described in Example 14.3b?

  1. 80 mL
  2. 75 mL
  3. 70 mL
  4. 85 mL

Check Your Answer[2]

Source: “Exercise 14.3b” is adapted from “Example 6.3-2” in General Chemistry 1 & 2, a derivative of Chemistry (Open Stax) by Paul Flowers, Klaus Theopold, Richard Langley & William R. Robinson, licensed under CC BY 4.0.

Example 14.3c

Calculating Molarity from the Mass of Solute

Distilled white vinegar (Figure 14.3b) is a solution of acetic acid, CH3CO2H, in water. A 0.500-L vinegar solution contains 25.2 g of acetic acid. What is the concentration of the acetic acid solution in units of molarity?

A label on a container is shown. The label has a picture of a salad with the words “Distilled White Vinegar,” and, “Reduced with water to 5% acidity,” written above it.
Figure 14.3b: Distilled white vinegar is a solution of acetic acid in water. (credit: modification of work by HomeSpot HQ, CC BY 2.0)

Solution

As in previous textbox shaded, the definition of molarity is the primary equation used to calculate the quantity sought. In this case, the mass of solute is provided instead of its molar amount, so we must use the solute’s molar mass to obtain the amount of solute in moles:

[latex]M = \frac{\text{mol solute}}{\text{L solution}} = \frac{25.2 \;\text{g CH}_3\text{CO}_2\text{H} \times \frac{1 \;\text{mol CH}_2\text{CO}_2\text{H}}{60.052 \;\text{g CH}_2\text{CO}_2\text{H}}}{0.500 \;\text{L solution}} = 0.839 \;M[/latex]
[latex]\begin{array}{r @{{}={}} l} M & = \frac{\text{mol solute}}{\text{L solution}} = 0.839\;M \\[1em] M & = \frac{0.839 \;\text{mol solute}}{1.00 \;\text{L solution}} \end{array}[/latex]

Exercise 14.3c

Calculate the molarity of 6.52 g of CoCl2 (128.9 g/mol) dissolved in an aqueous solution with a total volume of 75.0 mL.

Check Your Answer[3]

Example 14.3d

Determining the Mass of Solute in a Given Volume of Solution

How many grams of NaCl are contained in 0.250 L of a 5.30-M solution?

Solution

The volume and molarity of the solution are specified, so the amount (mol) of solute is easily computed as demonstrated in 14.2b:

[latex]M = \;\frac{\text{mol solute}}{\text{L solution}}[/latex]
[latex]\text{mol solute} = M \times \text{L solution}[/latex]
[latex]\text{mol solute} = 5.30 \;\frac{\text{mol NaCl}}{\text{L}} \times 0.250 \;\text{L} = 1.325 \;\text{mol NaCl}[/latex]

Finally, this molar amount is used to derive the mass of NaCl:

[latex]1.325 \;\text{mol NaCl} \times \frac{58.44 \;\text{g NaCl}}{\text{mol NaCl}} = 77.4 \;\text{g NaCl}[/latex]

Exercise 14.3d

How many grams of CaCl2 (110.98 g/mol) are contained in 250.0 mL of a 0.200-M solution of calcium chloride?

Check Your Answer[4]

When performing stepwise calculations, as in Example 4, it is important to refrain from rounding any intermediate calculation results, which can lead to rounding errors in the final result. In Example 4, the molar amount of NaCl computed in the first step, 1.325 mol, would be properly rounded to 1.32 mol if it were to be reported; however, although the last digit (5) is not significant, it must be retained as a guard digit in the intermediate calculation. If we had not retained this guard digit, the final calculation for the mass of NaCl would have been 77.1 g, a difference of 0.3 g.

In addition to retaining a guard digit for intermediate calculations, we can also avoid rounding errors by performing computations in a single step (see Example 14.3e). This eliminates intermediate steps so that only the final result is rounded.

Example 14.3e

Determining the Volume of Solution Containing a Given Mass of Solute

In Example 14.3c, we found the typical concentration of vinegar to be 0.839 M. What volume of vinegar contains 75.6 g of acetic acid?

Solution

First, use the molar mass to calculate moles of acetic acid from the given mass:

[latex]\text{g solute} \times \frac{\text{mol solute}}{\text{g solute}} = \text{mol solute}[/latex]

Then, use the molarity of the solution to calculate the volume of solution containing this molar amount of solute:

[latex]\text{mol solute} \times \frac{\text{L solution}}{\text{mol solute}} = \text{L solution}[/latex]

Combining these two steps into one yields:

[latex]\text{g solute} \times \frac{\text{mol solute}}{\text{g solute}} \times \frac{\text{L solution}}{\text{mol solute}} = \text{L solution}[/latex][latex]75.6 \;\text{g CH}_3\text{CO}_2\text{H} (\frac{\text{mol CH}_3\text{CO}_2\text{H}}{60.05 \;\text{g}}) (\frac{\text{L solution}}{0.839 \;\text{mol CH}_3\text{CO}_2\text{H}}) = 1.50 \;\text{L solution}[/latex]

Exercise 14.3e

Check Your Learning Exercise (Text Version)

What volume of a 1.50-M KBr solution contains 66.0 g KBr?

  1. 0.370 L
  2. 0.250 L
  3. 0.983 L
  4. 0.137 L

Check Your Answer[5]

Source: “Exercise 14.3e” is adapted from “Example 6.3-5” in General Chemistry 1 & 2, a derivative of Chemistry (Open Stax) by Paul Flowers, Klaus Theopold, Richard Langley & William R. Robinson, licensed under CC BY 4.0.

Dilution of Solutions

Dilution is the process whereby the concentration of a solution is lessened by the addition of solvent. For example, we might say that a glass of iced tea becomes increasingly diluted as the ice melts. The water from the melting ice increases the volume of the solvent (water) and the overall volume of the solution (iced tea), thereby reducing the relative concentrations of the solutes that give the beverage its taste (Figure 14.3c).

This figure shows two graduated cylinders side-by-side. The first has about half as much blue liquid as the second. The blue liquid is darker in the first cylinder than in the second.
Figure 14.3c: Both solutions contain the same mass of copper nitrate. The solution on the right is more dilute because the copper nitrate is dissolved in more solvent. (credit: Mark Ott in Chemistry (OpenStax), CC BY 4.0).

Dilution is also a common means of preparing solutions of a desired concentration. By adding solvent to a measured portion of a more concentrated stock solution, we can achieve a particular concentration. For example, commercial pesticides are typically sold as solutions in which the active ingredients are far more concentrated than is appropriate for their application. Before they can be used on crops, the pesticides must be diluted. This is also a very common practice for the preparation of a number of common laboratory reagents (Figure 14.3d).

This figure shows two photos. In the first, there is an empty glass container, 4.75 g of K M n O subscript 4 powder on a white circle, and a bottle of distilled water. In the second photo the powder and about half the water have been added to the glass container. The liquid in the glass container is almost black in color.
Figure 14.3d: A solution of KMnO4 is prepared by mixing water with 4.74 g of KMnO4 in a flask. (credit: modification of work by Mark Ott in Chemistry (OpenStax), CC BY 4.0).

A simple mathematical relationship can be used to relate the volumes and concentrations of a solution before and after the dilution process. According to the definition of molarity, the molar amount of solute in a solution is equal to the product of the solution’s molarity and its volume in litres:

[latex]n = ML[/latex]

Expressions like these may be written for a solution before and after it is diluted:

[latex]n_1 = M_1L_1[/latex]
[latex]n_2 = M_2L_2[/latex]

where the subscripts “1” and “2” refer to the solution before and after the dilution, respectively. Since the dilution process does not change the amount of solute in the solution,n1 = n2. Thus, these two equations may be set equal to one another:

[latex]M_1L_1 = M_2L_2[/latex]

This relation is commonly referred to as the dilution equation. Although we derived this equation using molarity as the unit of concentration and litres as the unit of volume, other units of concentration and volume may be used, so long as the units properly cancel per the factor-label method. Reflecting this versatility, the dilution equation is often written in the more general form:

[latex]C_1V_1 = C_2V_2[/latex]

where C and V are concentration and volume, respectively.

Exercise 14.3f

Practice using the following PhET simulation: Concentration.

Activity source: Simulation by PhET Interactive Simulations, University of Colorado Boulder, licensed under CC-BY-4.0

Exercise 14.3g

Practice using the following PhET simulation: Molarity

Activity source: Simulation by PhET Interactive Simulations, University of Colorado Boulder, licensed under CC-BY-4.0

Example 14.3f

Determining the Concentration of a Diluted Solution

If 0.850 L of a 5.00-M solution of copper nitrate, Cu(NO3)2, is diluted to a volume of 1.80 L by the addition of water, what is the molarity of the diluted solution?

Solution

We are given the volume and concentration of a stock solution, V1 and C1, and the volume of the resultant diluted solution, V2. We need to find the concentration of the diluted solution, C2. We thus rearrange the dilution equation in order to isolate C2:

[latex]C_1V_1 = C_2V_2[/latex]
[latex]C_2 = \frac{C_1V_1}{V_2}[/latex]

Since the stock solution is being diluted by more than two-fold (volume is increased from 0.85 L to 1.80 L), we would expect the diluted solution’s concentration to be less than one-half 5 M. We will compare this ballpark estimate to the calculated result to check for any gross errors in computation (for example, such as an improper substitution of the given quantities). Substituting the given values for the terms on the right side of this equation yields:

[latex]C_2 = \frac{0.850 \;\text{L} \times 5.00 \frac{\text{mol}}{\text{L}}}{1.80 \;\text{L}} = 2.36 \;M[/latex]

This result compares well to our ballpark estimate (it’s a bit less than one-half the stock concentration, 5 M).

Exercise 14.3h

Check Your Learning Exercise (Text Version)

What is the concentration of the solution that results from diluting 25.0 mL of a 2.04-M solution of CH3OH to 500.0 mL?

  1. 0.102 M CH3OH
  2. 0.202 M CH3OH
  3. 0.205 M CH3OH
  4. 0.703 M CH3OH

Check Your Answer[6]

Source: “Exercise 14.3h” is adapted from “Example 6.3-6” in General Chemistry 1 & 2, a derivative of Chemistry (Open Stax) by Paul Flowers, Klaus Theopold, Richard Langley & William R. Robinson, licensed under CC BY 4.0.

Example 14.3g

Volume of a Diluted Solution

What volume of 0.12 M HBr can be prepared from 11 mL (0.011 L) of 0.45 M HBr?

Solution

We are given the volume and concentration of a stock solution, V1 and C1, and the concentration of the resultant diluted solution, C2. We need to find the volume of the diluted solution, V2. We thus rearrange the dilution equation in order to isolate V2:

[latex]C_1V_1 = C_2V_2[/latex]
[latex]V_2 = \frac{C_1V_1}{C_2}[/latex]

Since the diluted concentration (0.12 M) is slightly more than one-fourth the original concentration (0.45 M), we would expect the volume of the diluted solution to be roughly four times the original volume, or around 44 mL. Substituting the given values and solving for the unknown volume yields:

[latex]V_2 = \frac{(0.45\;M)(0.011 \;\text{L})}{0.12 \; M}[/latex]
[latex]V_2 = 0.041 \;\text{L}[/latex]

The volume of the 0.12-M solution is 0.041 L (41 mL). The result is reasonable and compares well with our rough estimate.

Exercise 14.3i

A laboratory experiment calls for 0.125 M HNO3. What volume of 0.125 M HNO3 can be prepared from 0.250 L of 1.88 M HNO3?

Check Your Answer[7]

Example 14.3h

Volume of a Concentrated Solution Needed for Dilution

What volume of 1.59 M KOH is required to prepare 5.00 L of 0.100 M KOH?

Solution

We are given the concentration of a stock solution, C1, and the volume and concentration of the resultant diluted solution, V2 and C2. We need to find the volume of the stock solution, V1. We thus rearrange the dilution equation in order to isolate V1:

[latex]C_1V_1 = C_2V_2[/latex]
[latex]V_2 = \frac{C_2V_2}{C_2}[/latex]

Since the concentration of the diluted solution 0.100 M is roughly one-sixteenth that of the stock solution (1.59 M), we would expect the volume of the stock solution to be about one-sixteenth that of the diluted solution, or around 0.3 litres. Substituting the given values and solving for the unknown volume yields:

[latex]V_1 = \frac{(0.100\;M)(5.00 \;\text{L})}{1.59 \; M}[/latex]
[latex]V_1 = 0.314 \;\text{L}[/latex]

Thus, we would need 0.314 L of the 1.59-M solution to prepare the desired solution. This result is consistent with our rough estimate.

Exercise 14.3j

What volume of a 0.575-M solution of glucose, C6H12O6, can be prepared from 50.00 mL of a 3.00-M glucose solution?

Check Your Answer[8]

Visualizing Different Solutes in Solution

When seeking to understand compounds in solution, we must differentiate between the behaviour of covalent compounds and ionic compounds.  Assuming the solid dissolves, ionic compounds will dissociate into their ions. In contrast, for covalent compounds, the molecules of the compound remain intact.

So far in this section, we have been examining solutions of sugar (C6H12O6).  If we were to be able to see on the level of molecules, we might see a solution like that below (Figure 14.3e), where a triangle represents a molecule of glucose.  While the molecules move around in the solution once they are dissolved in water, the atoms in the molecule do not break apart. The covalent bonds are intact.

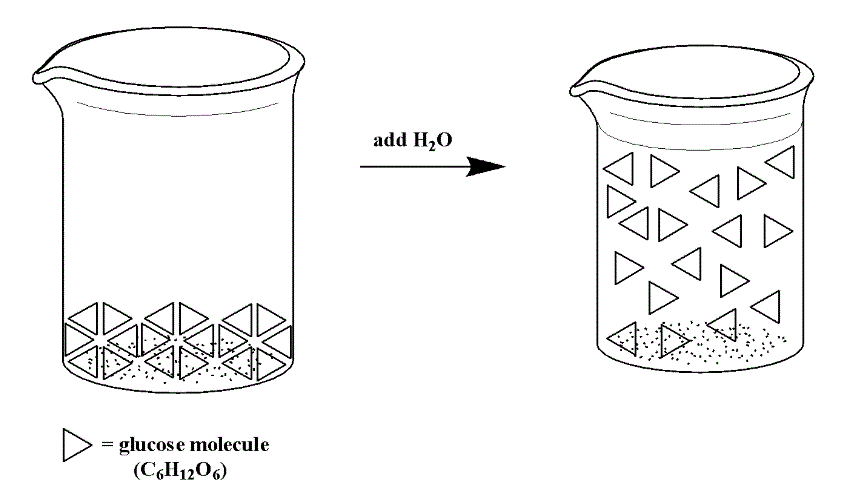
Glucose molecules, depicted as triangles in this diagram, when placed into a solvent such as water do not dissociate. Therefore, after a certain amount of time, the molecules flow around as complete molecules (still depicted as triangles).
Figure 14.3e: Glucose, when placed into a solvent such as water, does not dissociate. The molecules maintain their covalent bonds, and thus float around in solution as complete glucose molecules (triangles above) (General Chemistry I & II, CC BY 4.0)

In contrast, when an ionic compound dissolves in solution, the cations and anions are separated (they dissociate) and each ion is surrounded by water molecules.  We can depict the dissociation process for a compound like NaCl using the image below (Figure 14.3f):

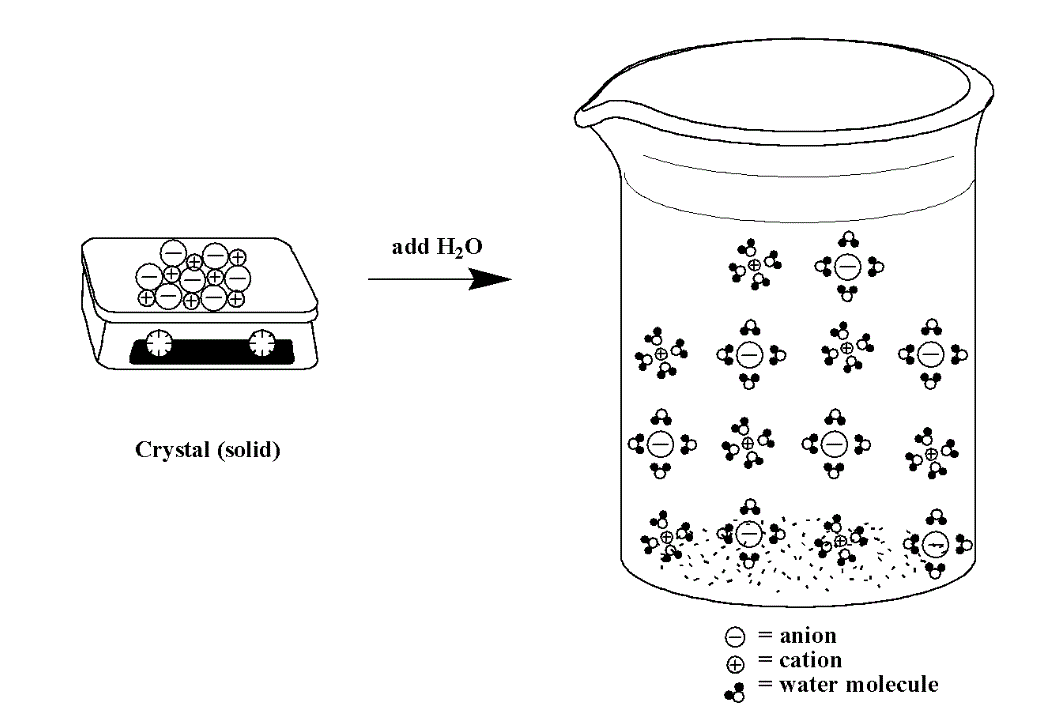
Ionic solids, depicted as combinations of positive symbols and negative symbols in this diagram, when placed into a polar solvent such as water will dissociate. Therefore, each positively charged ion and each negatively charged ion are separated from each other by the dipole moments on the water molecules, and float around separately in solution.
Figure 14.3f: Ionic solids, when placed into a polar solvent such as water, will undergo dissociation. Each ion is surrounded by water molecules due to dipole-dipole interactions, thus pulling the ionic compound apart into individual ions (General Chemistry I & II, CC BY 4.0)

If we leave out the water molecules (to make it easier to see the ions) below (Figure 14.3g) is an example of a sodium sulfate, Na2SO4, solution.  The sulfate anions will have a -2 charge and the sodium cations will have a +1 charge.

Sodium sulfate is an ionic solid. When it is placed into a polar solvent such as water, the individual sodium ions (depicted as positive symbols) and the individual sulfate ions (depicted as negative-2 symbols) are pulled apart by the dipole moments of the water molecules and thus float around separately in solution.
Figure 14.3g: Sodium sulfate (Na2SO4), when placed into a polar solvent such as water, will dissociate into individual Na+ ions and SO42- ions (General Chemistry I & II, CC BY 4.0)

Note that when the ionic compound dissociates, the covalent bonds of any polyatomic ions (like sulfate) remain intact.  Also note that the ions in solution are present in the same ratio as in the solid compound. In this case, there are 2 Na+ ions for every 1 SO42- ion.

Example 14.3h

Determining Moles of Ions in Ionic Compounds:

For each of the following, if 1 mole of the compound were to dissolve and dissociate, how many moles of ions would be present in:

  1. magnesium chloride?
  2. ammonium phosphate?

Solution:

  1. The formula for magnesium chloride is MgCl2. It is made of Mg2+ ions and Cl– ions.  If a mole of MgCl2 dissociates in solution, we’ll get 1 mole of Mg2+ ions and 2 moles of Cl– ions, for a total of 3 moles of ions.
  2. The formula for ammonium phosphate is (NH4)3PO4. It is made of NH4+ ions and PO43- ions.  If a mole of (NH4)3PO4 dissociates in solution, we’ll get 3 moles of NH4+ ions and 1 mole of PO43- ions, for a total of 4 moles of ions.

Exercise 14.3k

How many moles of each ion will be produced from 1 mole of ammonium sulfate?

Check Your Answer[9]

Because an ionic compound dissociates in solution, we can use our knowledge of molarity to describe the concentration of the compound in solution, OR the concentration of ions in solution.

Example 14.3i

Relating Concentrations of a Compound with Concentrations of its Ions in Solution

If you have a solution that is 0.5 M potassium sulfate, what is the concentration of potassium ions in solution? of sulfate ions in solution?

Solution

To answer the questions above, we want to know how many moles of each ion are present in a litre of solution.  We are given that the solution is 0.5 M K2SO4.  Given the definition of molarity, we can express the following:

[latex]0.5 \;\text{M K}_2\text{SO}_4 = \frac{0.5 \;\text{mol K}_2\text{SO}_4}{1 \;\text{L}}[/latex]

 

We can then use the appropriate relationship we know from the formula of potassium sulfate to make the appropriate conversions:

[latex]\frac{0.5 \;\text{mol K}_2\text{SO}_4}{1 \;\text{L}} \times \frac{2 \;\text{mol K}^+}{1 \;\text{mol K}_2\text{SO}_4} = \frac{1 \;\text{mol K}^+}{1 \;\text{L}} = \;\text{1 M K}^+[/latex]

[latex]\frac{0.5 \;\text{mol K}_2\text{SO}_4}{1 \;\text{L}} \times \frac{1 \;\text{mol SO}^{2-}_{4}}{1 \;\text{mol K}_2\text{SO}_4} = \frac{0.5 \;\text{mol SO}^{2-}_{4}}{1 \;\text{L}} = \;\text{0.5 M SO}^{2-}_{4}[/latex]

Does this result make sense?  We see that the concentration of potassium ions is twice that of the sulfate ions.  Given that when the ions dissociate, there will be twice as many potassium ions present compared to sulfate ion, this result make sense.

Exercise 14.3l

If you have a 1.3 M solution of ammonium carbonate, (NH4)2CO3, what is the concentration of each ion?

Check Your Answer[10]

Link to Interactive Learning Tools

Explore Dissociation from the Physics Classroom.

Explore Molarity Ranking Tasks from the Physics Classroom.

Explore Molarity Calculations from the Physics Classroom.

Key Equations

  • [latex]M = \frac{\text{mol solute}}{\text{L solution}}[/latex]
  • C1V1 = C2V2

Attribution & References

Except where otherwise noted, this page is adapted by Gregory A. Anderson from “6.3 Molarity” In General Chemistry 1 & 2 by Rice University, a derivative of Chemistry (Open Stax) by Paul Flowers, Klaus Theopold, Richard Langley & William R. Robinson and is licensed under CC BY 4.0. ​Access for free at Chemistry (OpenStax)​ .
  1. 0.05 M ↵
  2. 80 mL ↵
  3. 0.674 M ↵
  4. 5.55 g CaCl2 ↵
  5. 0.370 L ↵
  6. 0.102 M CH3OH ↵
  7. 3.76 L ↵
  8. 0.261 L ↵
  9. 2 moles of NH4+, 1 mole of SO42- ↵
  10. 2.6 M NH4+, 1.3 M CO32- ↵
definition

License

Icon for the Creative Commons Attribution 4.0 International License

Enhanced Introductory College Chemistry Copyright © 2023 by Gregory Anderson; Caryn Fahey; Jackie MacDonald; Adrienne Richards; Samantha Sullivan Sauer; J.R. van Haarlem; and David Wegman is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book