9.3 Limiting Reactants

Gregory Anderson; Caryn Fahey; Jackie MacDonald; Adrienne Richards; Samantha Sullivan Sauer; J.R. van Haarlem; David Wegman

9.3 Limiting Reactants

Learning Objectives

By the end of this section, you will be able to:

Explain the concepts of limiting reactants/reagents

The relative amounts of reactants and products represented in a balanced chemical equation are often referred to as stoichiometric amounts. All the exercises of the preceding module involved stoichiometric amounts of reactants. For example, when calculating the amount of product generated from a given amount of reactant, it was assumed that any other reactants required were available in stoichiometric amounts (or greater). In this module, more realistic situations are considered, in which reactants are not present in stoichiometric amounts.

Indigenous Perspective: Science of Bannock

Bannock is a staple food in many Indigenous communities throughout Canada. Here is an Anishinaabeg example of the science of Bannock.

Watch The Science of Bannock (23 mins)

Video source: Canadian Light Source. (2021, August 9). The science of bannock [Video]. YouTube.

Limiting Reactant

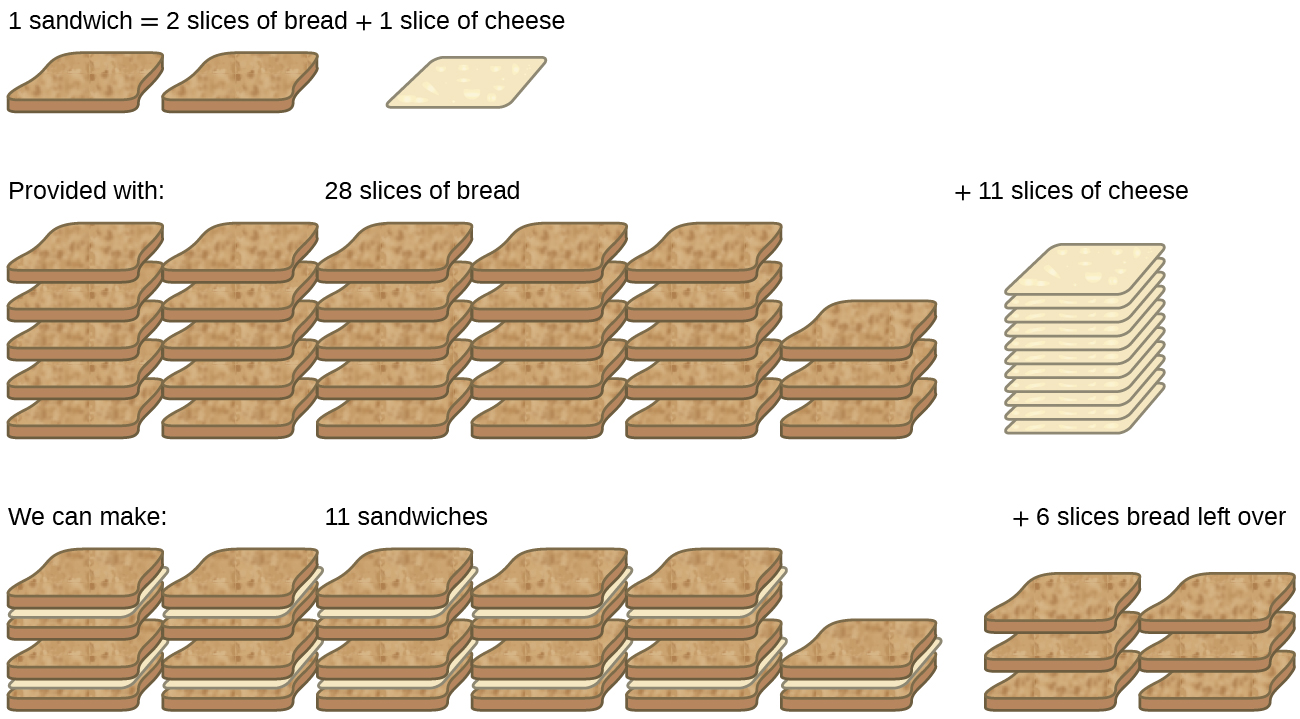
Consider another food analogy, making grilled cheese sandwiches (Figure 9.3a):

[latex]1 \;\text{slice of cheese} + 2 \;\text{slices of bread} \longrightarrow 1\;\text{sandwich}[/latex]

Stoichiometric amounts of sandwich ingredients for this recipe are bread and cheese slices in a 2:1 ratio. Provided with 28 slices of bread and 11 slices of cheese, one may prepare 11 sandwiches per the provided recipe, using all the provided cheese and having six slices of bread left over. In this scenario, the number of sandwiches prepared has been limited by the number of cheese slices, and the bread slices have been provided in excess.

This figure has three rows showing the ingredients needed to make a sandwich. The first row reads, “1 sandwich = 2 slices of bread + 1 slice of cheese.” Two slices of bread and one slice of cheese are shown. The second row reads, “Provided with: 28 slices of bread + 11 slices of cheese.” There are 28 slices of bread and 11 slices of cheese shown. The third row reads, “We can make: 11 sandwiches + 6 slices of bread left over.” 11 sandwiches are shown with six extra slices of bread. — **Figure 9.3a:** Sandwich making can illustrate the concepts of limiting and excess reactants (credit: *Chemistry (OpenStax)*, CC BY 4.0).

Consider this concept now with regard to a chemical process, the reaction of hydrogen with chlorine to yield hydrogen chloride:

[latex]\text{H}_2(s) + \text{Cl}_2(g) \longrightarrow 2\text{HCl}(g)[/latex]

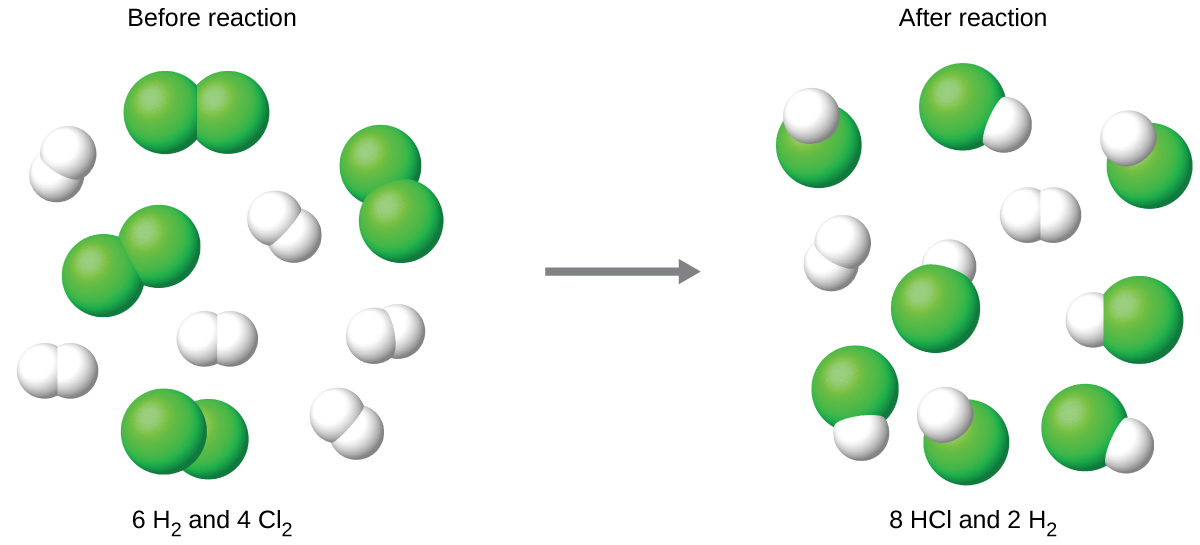
The balanced equation shows the hydrogen and chlorine react in a 1:1 stoichiometric ratio. If these reactants are provided in any other amounts, one of the reactants will nearly always be entirely consumed, thus limiting the amount of product that may be generated. This substance is the limiting reactant, and the other substance is the excess reactant. Identifying the limiting and excess reactants for a given situation requires computing the molar amounts of each reactant provided and comparing them to the stoichiometric amounts represented in the balanced chemical equation. For example, imagine combining 3 moles of H₂ and 2 moles of Cl₂. This represents a 3:2 (or 1.5:1) ratio of hydrogen to chlorine present for reaction, which is greater than the stoichiometric ratio of 1:1. Hydrogen, therefore, is present in excess, and chlorine is the limiting reactant. Reaction of all the provided chlorine (2 mol) will consume 2 mol of the 3 mol of hydrogen provided, leaving 1 mol of hydrogen unreacted.

An alternative approach to identifying the limiting reactant involves comparing the amount of product expected for the complete reaction of each reactant. Each reactant amount is used to separately calculate the amount of product that would be formed per the reaction’s stoichiometry. The reactant yielding the lesser amount of product is the limiting reactant. For the example in the previous paragraph, complete reaction of the hydrogen would yield

[latex]\text{mol HCl produced} = 3 \;\text{mol H}_2 \times \frac{2 \;\text{mol HCl}}{1 \;\text{mol H}_2} = 6 \;\text{mol HCl}[/latex]

Complete reaction of the provided chlorine would produce

[latex]\text{mol HCl produced} = 2 \;\text{mol Cl}_2 \times \frac{2 \;\text{mol HCl}}{1 \;\text{mol Cl}_2} = 4 \;\text{mol HCl}[/latex]

The chlorine will be completely consumed once 4 moles of HCl have been produced. Since enough hydrogen was provided to yield 6 moles of HCl, there will be unreacted hydrogen remaining once this reaction is complete. Chlorine, therefore, is the limiting reactant and hydrogen is the excess reactant (Figure 9.3b).

Molecular models are used to show before and after a reaction has taken place, with a right pointing reaction arrow in between. To the left of the reaction arrow there are four molecules each consisting of two green spheres bonded together. There are also six molecules each consisting of two smaller, white spheres bonded together. Above these molecules is the label, “Before reaction,” and below these molecules is the label, “6 H subscript 2 and 4 C l subscript 2.” To the right of the reaction arrow, there are eight molecules each consisting of one green sphere bonded to a smaller white sphere. There are also two molecules each consisting of two white spheres bonded together. Above these molecules is the label, “After reaction,” and below these molecules is the label, “8 H C l and 2 H subscript 2.” — **Figure 9.3b:** When H₂ and Cl₂ are combined in nonstoichiometric amounts, one of these reactants will limit the amount of HCl that can be produced. This illustration shows a reaction in which hydrogen is present in excess and chlorine is the limiting reactant (credit: *Chemistry (OpenStax)*, CC BY 4.0).

Exercise 9.3a

Practice using the following PhET simulation: Reactants, Products, and Leftovers

Activity source: Simulation by PhET Interactive Simulations, University of Colorado Boulder, licensed under CC-BY-4.0

Example 9.3a

Identifying the Limiting Reactant and Calculate Max Amount of Product Produced

Silicon nitride is a very hard, high-temperature-resistant ceramic used as a component of turbine blades in jet engines. It is prepared according to the following equation:

[latex]3\text{Si}(s) + 2\text{N}_2(g) \longrightarrow \text{Si}_3 \text{N}_4(s)[/latex]

A) Which is the limiting reactant when 2.00 g of Si and 1.50 g of N₂ react?

B) How many grams of silicon nitride are produced?

Solution

A) Compute the provided molar amounts of reactants, and then compare these amounts to the balanced equation to identify the limiting reactant.

[latex]\text{mol Si} = 2.00 \;\rule[0.5ex]{1.75em}{0.1ex}\hspace{-1.75em}\text{g Si} \times \frac{1 \;\text{mol Si}}{28.09 \;\rule[0.25ex]{1.25em}{0.1ex}\hspace{-1.25em}\text{g Si}} = 0.0712 \;\text{mol Si}[/latex]

[latex]\text{mol N}_2 = 1.50 \;\rule[0.5ex]{2em}{0.1ex}\hspace{-2em}\text{g N}_2 \times \frac{1 \;\text{mol N}_2}{28.09 \rule[0.25ex]{1.5em}{0.1ex}\hspace{-1.5em}\;\text{g N}_2} = 0.0535 \;\text{mol N}_2[/latex]

The provided Si:N₂ molar ratio is:

[latex]\frac{0.0712 \;\text{mol Si}}{0.0535 \;\text{mol N}_2} = \frac{1.33 \;\text{mol Si}}{1 \text{mol N}_2}[/latex]

The stoichiometric Si:N₂ ratio is:

[latex]\frac{3 \;\text{mol Si}}{2 \;\text{mol N}_2} = \frac{1.5 \;\text{mol Si}}{1 \;\text{mol N}_2}[/latex]

Comparing these ratios shows that Si is provided in a less-than-stoichiometric amount, and so is the limiting reactant.

Alternatively, compute the amount of product expected for complete reaction of each of the provided reactants. The 0.0712 moles of silicon would yield

[latex]\text{mol Si}_3 \text{N}_4 \;\text{produced} = 0.0712 \;\text{mol Si} \times \frac{1 \;\text{mol Si}_3 \text{N}_4}{3 \;\text{mol Si}} = \\0.0237 \;\text{mol Si}_3 \text{N}_4[/latex]

while the 0.0535 moles of nitrogen would produce

[latex]\text{mol Si}_3 \text{N}_4 \;\text{produced} = 0.0535 \;\text{mol N}_2 \times \frac{1 \;\text{mol Si}_3 \text{N}_4}{2 \;\text{mol N}_2} = \\0.0268 \;\text{mol Si}_3 \text{N}_4[/latex]

Since silicon yields the lesser amount of product, it is the limiting reactant.

B) In order to determine the maximum amount of product produced, first the limiting reactant has to be determined. In part A, the limiting reactant was determined to be silicon. Therefore, the moles of silicon nitride produced by silicon will be used to calculate how many grams of silicon nitride is produced.

[latex]\text{0.0237 mol Si}_3 \text{N}_4 \;\times \frac{140.28 \;\text{g Si}_3 \text{N}_4}{1 \;\text{mol Si}_3 \text{N}_4} = 3.32 \;\text{grams Si}_3 \text{N}_4[/latex]

Exercise 9.3b

Which is the limiting reactant when 5.00 g of H₂ and 10.0 g of O₂ react and form water? How many grams of water is produced?

Check Your Answer^[1]

Attribution & References

Except where otherwise noted, this page is adapted by Adrienne Richards from “7.4 Reaction Yields” In General Chemistry 1 & 2 by Rice University, a derivative of Chemistry (Open Stax) by Paul Flowers, Klaus Theopold, Richard Langley & William R. Robinson and is licensed under CC BY 4.0. Access for free at Chemistry (OpenStax)

O₂ is limiting reactant, 22.5 g H₂O produced ↵

License

Icon for the Creative Commons Attribution 4.0 International License

Enhanced Introductory College Chemistry Copyright © 2023 by Gregory Anderson; Caryn Fahey; Jackie MacDonald; Adrienne Richards; Samantha Sullivan Sauer; J.R. van Haarlem; and David Wegman is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.