7.2 Molecular Mass, Avogadro’s Number and The Mole

Learning Objectives

By the end of this section, you will be able to:

  • Calculate molecular masses (or numerically equivalent molar masses) for covalent and ionic compounds
  • Explain the relation between mass, moles, and numbers of atoms or molecules, and perform calculations deriving quantities from one another

We can argue that modern chemical science began when scientists started exploring the quantitative as well as the qualitative aspects of chemistry. For example, Dalton’s atomic theory was an attempt to explain the results of measurements that allowed him to calculate the relative masses of elements combined in various compounds. Understanding the relationship between the masses of atoms and the chemical formulas of compounds allows us to quantitatively describe the composition of substances.

Molecular Mass for Substances

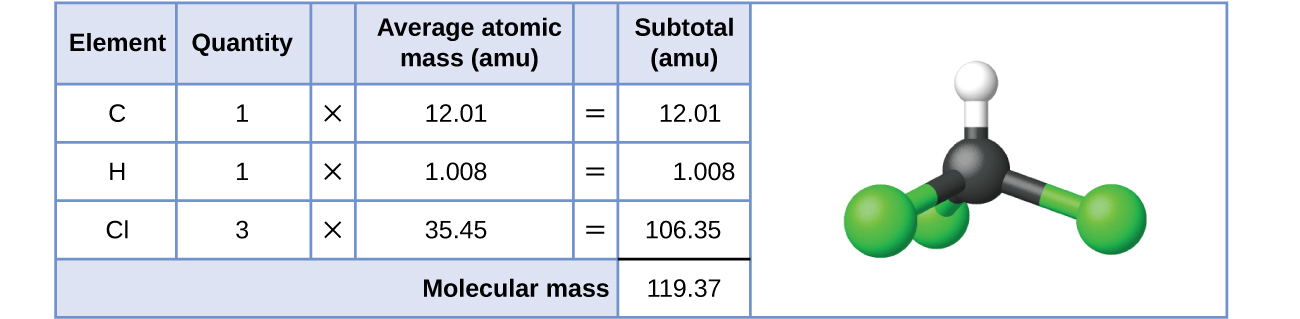
The formula represents the numbers and types of atoms composing a single molecule of the substance; therefore, the formula mass may be correctly referred to as a molecular mass. This value of the formula mass can also be used to consider a substance’s molar mass (numerically equivalent to molecular mass per 1 mole of substance as discussed in section 7.1). Consider chloroform (CHCl3), a covalent compound once used as a surgical anesthetic and now primarily used in the production of the “anti-stick” polymer, Teflon. The molecular formula of chloroform (trichloromethane) indicates that a single molecule contains one carbon atom, one hydrogen atom, and three chlorine atoms. The average molar mass of a chloroform molecule is therefore equal to the sum of the average atomic masses of these atoms. Figure 7.2a outlines the calculations used to derive the molecular mass of chloroform, which is 119.37 amu. The molecular mass of 119.37 amu expressed as a molar mass is 119.37 g/mol.

A table and diagram are shown. The table is made up of six columns and five rows. The header row reads: “Element,” “Quantity,” a blank space, “Average atomic mass (a m u),” a blank space, and “Subtotal (a m u).” The first column contains the symbols “C,” “H,” “C l” and a blank, merged cell that runs the width of the first five columns. The second column contains the numbers “1,” “1,” and “3” as well as the merged cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “12.01,” “1.008,” and “35.45” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values “12.01,” “1.008,” “106.35,” and “119.37.” There is a thick black line below the number 106.35. The merged cell under the first five columns reads “Molecular mass.” To the left of the table is a diagram of a molecule. Three green spheres are attached to a slightly smaller black sphere, which is also attached to a smaller white sphere. The green spheres lie beneath and to the sides of the black sphere while the white sphere is located straight up from the black sphere.
Figure 7.2a: The average mass of a chloroform molecule, CHCl3, is 119.37 amu, which is the sum of the average atomic masses of each of its constituent atoms. The model shows the molecular structure of chloroform (credit: Chemistry (OpenStax), CC BY 4.0).

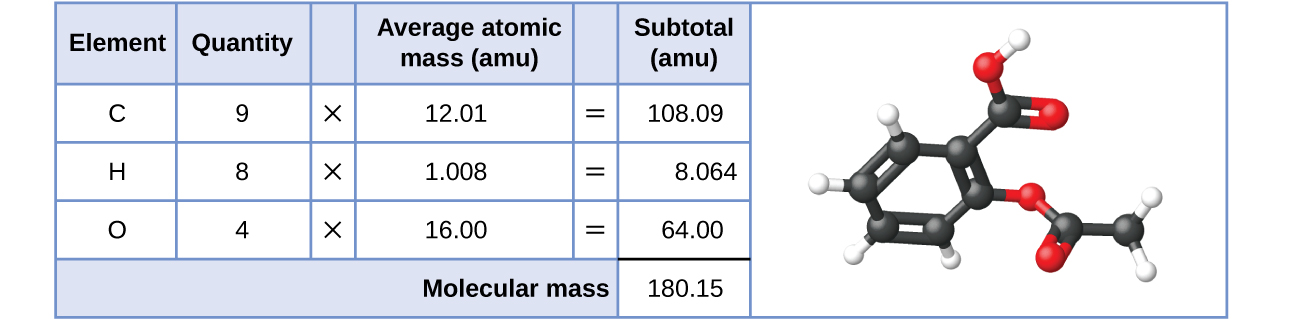
Likewise, the molecular mass of an aspirin molecule, C9H8O4, is the sum of the atomic masses of nine carbon atoms, eight hydrogen atoms, and four oxygen atoms, which amounts to 180.15 amu (Figure 7.2b) or 180.15 g/mol (molar mass).

A table and diagram are shown. The table is made up of six columns and five rows. The header row reads: “Element,” “Quantity,” a blank space, “Average atomic mass (a m u),” a blank space, and “Subtotal (a m u).” The first column contains the symbols “C,” “H,” “O,” and a merged cell. The merged cell runs the length of the first five columns. The second column contains the numbers “9,” “8,” and “4” as well as the merged, cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “12.01,” “1.008,” and “16.00” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values: “108.09,” “8.064,” “64.00,” and “180.15.” There is a thick black line below the number 64.00. The merged cell under the first five columns reads “Molecular mass.” To the left of the table is a diagram of a molecule. Six black spheres are located in a six-sided ring and connected by alternating double and single black bonds. Attached to each of the four black spheres is one smaller white sphere. Attached to the farthest right black sphere is a red sphere, connected to two more black spheres, all in a row. Attached to the last black sphere of that row are two more white spheres. Attached to the first black sphere of that row is another red sphere. A black sphere, attached to two red spheres and a white sphere is attached to the black sphere on the top right of the six-sided ring.
Figure 7.2b: The average mass of an aspirin molecule is 180.15 amu. The model shows the molecular structure of aspirin, C9H8O4 (credit: Chemistry (OpenStax), CC BY 4.0).

Example 7.2a

Computing Molecular Mass for a Covalent Compound

Ibuprofen, C13H18O2, is a covalent compound and the active ingredient in several popular nonprescription pain medications, such as Advil and Motrin. What is the molecular mass (amu) for this compound? What is the molar mass?

Solution

Molecules of this compound are comprised of 13 carbon atoms, 18 hydrogen atoms, and 2 oxygen atoms. Following the approach described above, the average molecular mass for this compound is, therefore:

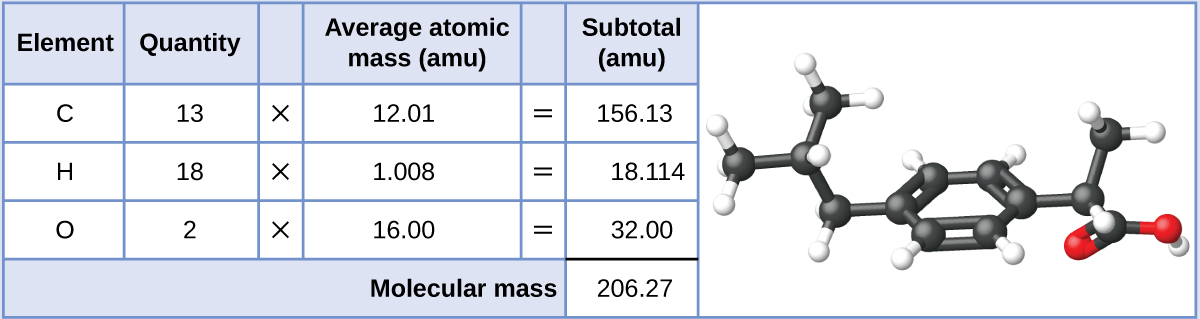
A table is shown that is made up of six columns and five rows. The header row reads: “Element,” “Quantity,” a blank space, “Average atomic mass (a m u),” a blank space, and “Subtotal (a m u).” The first column contains the symbols “C,” “H,” “O,” and a merged cell. The merged cell runs the length of the first five columns. The second column contains the numbers “13,” “8,” and “2” as well as the merged cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “12.01,” “1.008,” and “16.00” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values “156.13,” “18.114,” “32.00,” and “206.27.” There is a thick black line below the number 32.00. The merged cell under the first five columns reads “Molecular mass.” To the right is a ball-and-stick model of the structure. At the center, it shows six black spheres arranged in a six-sided ring with alternating double bonds. The two black spheres at the top and bottom of the six-sided ring are each bonded to one, smaller, white sphere. The black sphere on the left side of the six-sided ring is connect to another black sphere. This sphere is connected to two smaller, white spheres and another black sphere. This black sphere is connected to one, smaller white sphere, and two other black spheres. Each of these last two black spheres is connected to two smaller, white spheres. The black sphere on the right side of the six-sided ring is connected to another black sphere. This black sphere is connected to one smaller, white sphere and two other black spheres. The black sphere that is connected to it and is situated to the top right is connected to two smaller, white spheres. The black sphere connected towards the bottom right is connected to two red spheres. It forms a double bond with one of these red spheres and the other red sphere is connected to a smaller, white sphere.

The molecular mass is 206.27 amu. The molar mass is 206.27 g/mol.

Exercise 7.2a

Acetaminophen, C8H9NO2, is a covalent compound and the active ingredient in several popular nonprescription pain medications, such as Tylenol. What is the molecular mass (amu) for this compound? What is the molar mass?

Check Your Answer[1]

Example 7.2b

Computing Molecular Mass for an Ionic Compound

Aluminum sulfate, Al2(SO4)3, is an ionic compound that is used in the manufacture of paper and in various water purification processes. What is the molecular mass (amu) of this compound? What is the molar mass?

Solution

The formula for this compound indicates it contains Al3+ and SO42− ions combined in a 2:3 ratio. For purposes of computing a formula mass, it is helpful to rewrite the formula in the simpler format, Al2S3O12. Following the approach outlined above, the formula mass for this compound is calculated as follows:

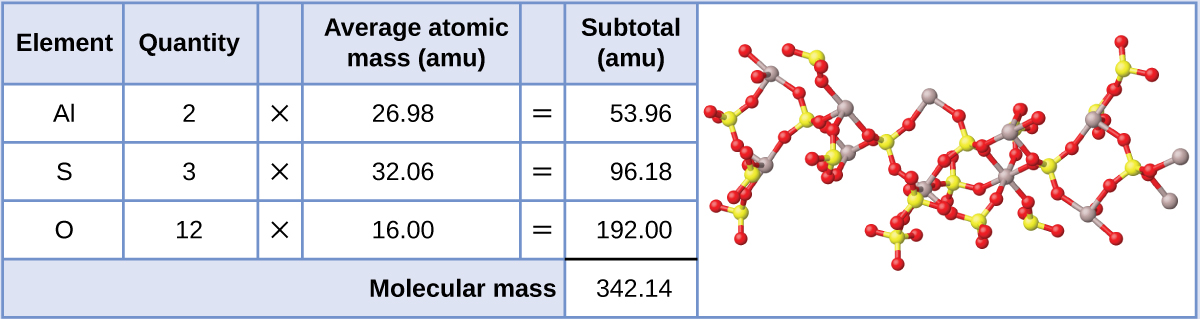
A table is shown that is made up of six columns and five rows. The header row reads: “Element,” “Quantity,” a blank space, “Average atomic mass (a m u),” a blank space, and “Subtotal (a m u).” The first column contains the symbols “A l,” “S,” “O,” and a merged cell. The merged cell runs the length of the first five columns. The second column contains the numbers “2,” “3,” and “12” as well as the merged cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “26.98,” “32.06,” and “16.00” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values “53.96,” “96.18,” “192.00,” and “342.14.” There is a thick black line under the number 192.00. The merged cell under the first five columns reads “Molecular mass.” To the right of this table is a ball-and-stick structure. It shows yellow and grey sphere connected to red spheres in a complex pattern. The yellow and grey spheres are similar in size, but the red spheres appear to be smaller by comparison.

The molecular mass is 342.14 amu. The molar mass is 342.14 g/mol.

Exercise 7.2b

Calcium phosphate, Ca3(PO4)2, is an ionic compound and a common anti-caking agent added to food products. What is the molecular mass (amu) of calcium phosphate? What is the molar mass?

Check Your Answer[2]

The Mole

To review, the mole is an amount unit similar to familiar units like pair, dozen, gross, etc. In section 7.1, we learned it can be used to count atoms. The mole provides a specific measure of the number of atoms or molecules in a bulk sample of matter. It provides a link between an easily measured macroscopic property, bulk mass, and an extremely important fundamental property, number of atoms, molecules, and so forth.

Recall that Avogadro’s number (NA) is a constant and is properly reported with an explicit unit of “per mole.” Therefore, we can use Avogadro’s number for counting molecules as well:

6.022 x 1023 molecules = 1 mole of molecules

Consistent with its definition as an amount unit, 1 mole of any compound contains the same number of molecules as 1 mole of any other compound. However, the molar mass of two different compounds will be different because their formula masses are different. The molar mass of a compound in grams is likewise numerically equivalent to its formula mass in amu (Figure 7.2c).

This photo shows two vials filled with a colorless liquid. It also shows two bowls: one filled with an off-white powder and one filled with a bright red powder.
Figure 7.2c: Each sample contains 6.02 × 1023 molecules or formula units—1.00 mol of the compound or element. Clock-wise from the upper left: 130.2 g of C8H17OH (1-octanol, formula mass 130.2 amu), 454.4 g of HgI2 (mercury(II) iodide, formula mass 454.4 amu), 32.0 g of CH3OH (methanol, formula mass 32.0 amu) and 256.5 g of S8 (sulfur, formula mass 256.5 amu). (credit: Sahar Atwa in Chemistry (OpenStax), CC BY 4.0).
Table 7.2a: Examples of elements average atomic mass, molar mass and atoms/mole. 
Element Average Atomic Mass (amu) Molar Mass (g/mol) Atoms/Mole
C 12.01 12.01 6.022 × 1023
H 1.008 1.008 6.022 × 1023
O 16.00 16.00 6.022 × 1023
Na 22.99 22.99 6.022 × 1023
Cl 35.45 35.45 6.022 × 1023

While the formula mass and molar mass of a compound are numerically equivalent, keep in mind that they are vastly different in terms of scale, as represented by the vast difference in the magnitudes of their respective units (amu versus g). To appreciate the enormity of the mole, consider a small drop of water weighing about 0.03 g (see Figure 7.2d). Although this represents just a tiny fraction of 1 mole of water (~18 g), it contains more water molecules than can be clearly imagined. If the molecules were distributed equally among the roughly seven billion people on earth, each person would receive more than 100 billion molecules.

A close-up photo of a water droplet on a leaf is shown. The water droplet is not perfectly spherical.
Figure 7.2d: The number of molecules in a single droplet of water is roughly 100 billion times greater than the number of people on earth. (credit: work by Tahlia Doyle, Unsplash license).

The relationships between formula mass, the mole, and Avogadro’s number can be applied to compute various quantities that describe the composition of compounds. For example, if we know the mass and chemical composition of a substance, we can determine the number of moles and calculate a number of atoms or molecules in the sample. Likewise, if we know the number of moles of a substance, we can derive the number of atoms or molecules and calculate the substance’s mass.

These relationships can be represented mathematically using the following expressions:

[latex]n = \frac{m}{M}[/latex]

Where: n = number of moles (mol)
             m = mass (g)
             M = molar mass (g/mol)
Number of atoms/ions/molecules = n x NA
Where: NA = 6.022 x 1023 atoms/ions/molecules
                 n = number of moles (mol)

Example 7.2c

Deriving Moles from Grams for an Element

According to nutritional guidelines from the US Department of Agriculture, the estimated average requirement for dietary potassium is 4.7 g. What is the estimated average requirement of potassium in moles?

Solution

The mass of K is provided, and the corresponding amount of K in moles is requested. Referring to the periodic table, the atomic mass of K is 39.10 amu, and so its molar mass is 39.10 g/mol. The given mass of K (4.7 g) is a bit more than one-tenth the molar mass (39.10 g), so a reasonable “ballpark” estimate of the number of moles would be slightly greater than 0.1 mol.

The molar amount of a substance may be calculated by dividing its mass (g) by its molar mass (g/mol):

This image shows two boxes, one on the left and one on the right. There is an arrow pointing from the left hand box to the right hand box to indicate the sequence to follow when converting mass to moles. The left hand box states the mass of K atoms in grams, the arrow to the right hand box states divide by molar mass which is in grams per mole, this leads to the right hand box that states the moles of K atoms in moles.

The factor-label method supports this mathematical approach since the unit “g” cancels and the answer has units of “mol:”

 

[latex]4.7 \;\rule[0.5ex]{1.5em}{0.1ex}\hspace{-1.5em}\text{g K} \times \frac{1 \;\text{mol K}}{39.10 \;\rule[0.5ex]{1.5em}{0.1ex}\hspace{-1.5em}\text{g K}} = 0.12 \;\text{mol K}[/latex]

The calculated magnitude (0.12 mol K) is consistent with our ballpark expectation, since it is a bit greater than 0.1 mol.

Exercise 7.2c

Beryllium is a light metal used to fabricate transparent X-ray windows for medical imaging instruments. How many moles of Be are in a thin-foil window weighing 3.24 g?

Check Your Answer[3]

Example 7.2d

Deriving Grams from Moles for an Element

A litre of air contains 9.2 × 10−4 mol argon. What is the mass of Ar in a litre of air?

Solution

The molar amount of Ar is provided and must be used to derive the corresponding mass in grams. Since the amount of Ar is less than 1 mole, the mass will be less than the mass of 1 mole of Ar, approximately 40 g. The molar amount in question is approximately one-one thousandth (~10−3) of a mole, and so the corresponding mass should be roughly one-one thousandth of the molar mass (~0.04 g):

This image shows two boxes, one on the left and one on the right. There is an arrow pointing from the left hand box to the right hand box to indicate the sequence to follow when converting moles to mass. The left hand box states the moles of Ar atoms in moles, the arrow to the right hand box states multiply by molar mass which is in grams per mole, this leads to the right hand box that states the mass of Ar atoms in grams.

In this case, logic dictates (and the factor-label method supports) multiplying the provided amount (mol) by the molar mass (g/mol):

[latex]9.2 \times 10^{-4} \;\rule[0.5ex]{3em}{0.1ex}\hspace{-3em}\text{mol Ar} \times \frac{39.95 \;\text{g Ar}}{1 \;\rule[0.5ex]{3em}{0.1ex}\hspace{-3em}\text{mol Ar}} = 0.037 \;\text{g Ar}[/latex]

The result is in agreement with our expectations, around 0.04 g Ar.

Exercise 7.2d

What is the mass of 2.561 mol of gold?

Check Your Answer[4]

Example 7.2e

Deriving Moles from Grams for a Compound

Our bodies synthesize protein from amino acids. One of these amino acids is glycine, which has the molecular formula C2H5O2N. How many moles of glycine molecules are contained in 28.35 g of glycine?

Solution

We can derive the number of moles of a compound from its mass by the following:

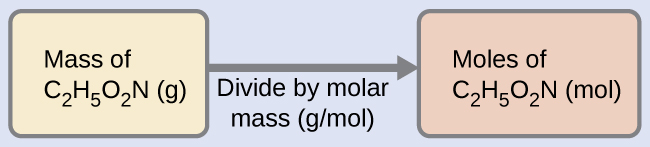
A diagram of two boxes connected by a right-facing arrow is shown. The box on the left contains the phrase, “Mass of C subscript 2 H subscript 5 O subscript 2 N ( g )” while the box on the right contains the phrase, “Moles of C subscript 2 H subscript 5 O subscript 2 N ( mol ).” There is a phrase under the arrow that says “Divide by molar mass (g / mol).”

The molar mass of glycine is required for this calculation, and it is computed in the same fashion as its molecular mass. One mole of glycine, C2H5O2N, contains 2 moles of carbon, 5 moles of hydrogen, 2 moles of oxygen, and 1 mole of nitrogen:

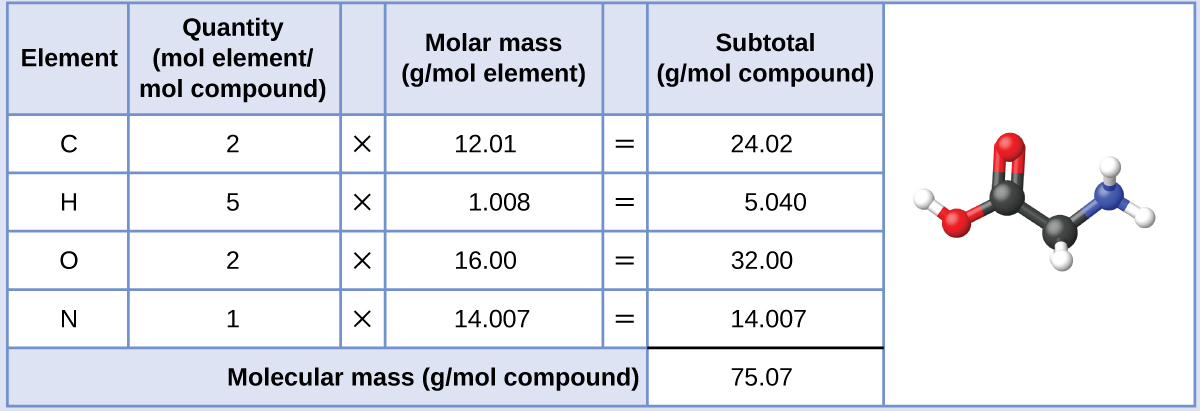
A table is shown that is made up of six columns and six rows. The header row reads: “Element,” “Quantity (mol element / mol compound,” a blank space, “Molar mass (g / mol element),” a blank space, and “Subtotal (a m u).” The first column contains the symbols “C,” “H,” “O,” “N,” and a merged cell. The merged cell runs the width of the first five columns. The second column contains the numbers “2,” “5,” “2,” and “1” as well as the merged cell. The third column contains the multiplication symbol in each cell except for the last, merged cell. The fourth column contains the numbers “12.01,” “1.008,” “16.00,” and “14.007” as well as the merged cell. The fifth column contains the symbol “=” in each cell except for the last, merged cell. The sixth column contains the values “24.02,” “5.040,” “32.00,” “14.007,” and “75.07.” There is a thick black line under the number 14.007. The merged cell under the first five columns reads “Molar mass (g / mol compound). There is a ball-and-stick drawing to the right of this table. It shows a black sphere that forms a double bond with a slightly smaller red sphere, a single bond with another red sphere, and a single bond with another black sphere. The red sphere that forms a single bond with the black sphere also forms a single bond with a smaller, white sphere. The second black sphere forms a single bond with a smaller, white sphere and a smaller blue sphere. The blue sphere forms a single bond with two smaller, white spheres each.

The provided mass of glycine (~28 g) is a bit more than one-third the molar mass (~75 g/mol), so we would expect the computed result to be a bit greater than one-third of a mole (~0.33 mol). Dividing the compound’s mass by its molar mass yields:

[latex]28.35 \;\rule[0.5ex]{3.5em}{0.1ex}\hspace{-3.5em}\text{g glycine}\times \frac{1 \;\text{mol glycine}}{75.07 \;\rule[0.5ex]{3.7em}{0.1ex}\hspace{-3.7em}\text{g glycine}} = 0.378 \;\text{mol glycine}[/latex]

This result is consistent with our rough estimate.

Exercise 7.2e

How many moles of sucrose, C12H22O11, are in a 25-g sample of sucrose?

Check Your Answer[5]

Example 7.2f

Deriving Grams from Moles for a Compound

Vitamin C is a covalent compound with the molecular formula C6H8O6. The recommended daily dietary allowance of vitamin C for children aged 4–8 years is 1.42 × 10−4 mol. What is the mass of this allowance in grams?

Solution

As for elements, the mass of a compound can be derived from its molar amount as shown:

A diagram of two boxes connected by a right-facing arrow is shown. The box on the left contains the phrase, “Moles of vitamin C ( mol )” while the one the right contains the phrase, “Mass of vitamin C ( g )”. There is a phrase under the arrow that says “Multiply by molar mass (g / mol).”

The molar mass for this compound is computed to be 176.124 g/mol. The given number of moles is a very small fraction of a mole (~10−4 or one-ten thousandth); therefore, we would expect the corresponding mass to be about one-ten thousandth of the molar mass (~0.02 g). Performing the calculation, we get:

[latex]1.42 \times 10^{-4} \;\rule[0.5ex]{6em}{0.1ex}\hspace{-6em}\text{mol vitamin C} \times \frac{176.124 \;\text{g vitamnin C}}{1 \;\rule[0.5ex]{6em}{0.1ex}\hspace{-6em}\text{mol vitamin C}} = 0.0250 \;\text{g vitamin C}[/latex]

 

This is consistent with the anticipated result.

Exercise 7.2f

What is the mass of 0.443 mol of hydrazine, N2H4?

Check Your Answer[6]

Example 7.2g

Deriving the Number of Atoms from Mass for an Element

Copper is commonly used to fabricate electrical wire (Figure 7.2e). How many copper atoms are in 5.00 g of copper wire?

Copper wire is composed of many, many atoms of Cu.
Figure 7.2e: Copper wire is composed of many, many atoms of Cu. (credit: work by Emilian Robert Vicol, CC BY 2.0).

Solution

The number of Cu atoms in the wire may be conveniently derived from its mass by a two-step computation: first calculating the molar amount of Cu, and then using Avogadro’s number (NA) to convert this molar amount to number of Cu atoms:This image is a diagram that shows the flow conversion in three boxes from mass to moles to atoms of copper (Cu) with a right hand arrow indicating the direction of the conversion. The first box states mass of Cu atoms in grams; a right hand arrow states divide by molar mass in grams per mole that leads to the second box; the second box states moles of Cu atoms in moles; a second right hand arrow states multiply by Avogadro's number (inverse mole) that leads to the third box; the third box states number of Cu atoms.Considering that the provided sample mass (5.00 g) is a little less than one-tenth the mass of 1 mole of Cu (~64 g), a reasonable estimate for the number of atoms in the sample would be on the order of one-tenth NA, or approximately 1022 Cu atoms. Carrying out the two-step computation yields:

[latex]5.00 \;\rule[0.5ex]{2em}{0.1ex}\hspace{-2em}\text{g Cu} \times \frac{1 \;\rule[0.5ex]{3em}{0.1ex}\hspace{-3em}\text{mol Cu}}{63.55 \;\rule[0.5ex]{2em}{0.1ex}\hspace{-2em}\text{g Cu}} \times \frac{6.022 \times 10^{23} \;\text{atoms Cu}}{1 \;\rule[0.5ex]{3em}{0.1ex}\hspace{-3em}\text{mol Cu}} = 4.74 \times 10^{22} \;\text{atoms Cu}[/latex]

 

The factor-label method yields the desired cancellation of units, and the computed result is on the order of 1022 as expected.

Exercise 7.2g

A prospector panning for gold in a river collects 15.00 g of pure gold. How many Au atoms are in this quantity of gold?

Check Your Answer[7]

Counting Neurotransmitter Molecules in the Brain

The brain is the control centre of the central nervous system (Figure 7.2f). It sends and receives signals to and from muscles and other internal organs to monitor and control their functions; it processes stimuli detected by sensory organs to guide interactions with the external world; and it houses the complex physiological processes that give rise to our intellect and emotions. The broad field of neuroscience spans all aspects of the structure and function of the central nervous system, including research on the anatomy and physiology of the brain. Great progress has been made in brain research over the past few decades, and the BRAIN Initiative, a federal initiative announced in 2013, aims to accelerate and capitalize on these advances through the concerted efforts of various industrial, academic, and government agencies.

A macroscopic top view of the human brain and a microscopic image of neural tissue are pictured. The neural tissue shows two large irregularly shaped masses, labelled “Neuron cells”, in a field of threadlike material interspersed with smaller, relatively round masses.
Figure 7.2f: (a) A typical human brain weighs about 1.5 kg and occupies a volume of roughly 1.1 L. (b) Information is transmitted in brain tissue and throughout the central nervous system by specialized cells called neurons (micrograph shows cells at 1600× magnification) (credit: Chemistry (OpenStax), CC BY 4.0).

Specialized cells called neurons transmit information between different parts of the central nervous system by way of electrical and chemical signals. Chemical signalling occurs at the interface between different neurons when one of the cells releases molecules (called neurotransmitters) that diffuse across the small gap between the cells (called the synapse) and bind to the surface of the other cell. These neurotransmitter molecules are stored in small intracellular structures called vesicles that fuse to the cell wall and then break open to release their contents when the neuron is appropriately stimulated. This process is called exocytosis (see Figure 7.2g). One neurotransmitter that has been very extensively studied is dopamine, C8H11NO2. Dopamine is involved in various neurological processes that impact a wide variety of human behaviours. Dysfunctions in the dopamine systems of the brain underlie serious neurological diseases such as Parkinson’s and schizophrenia.

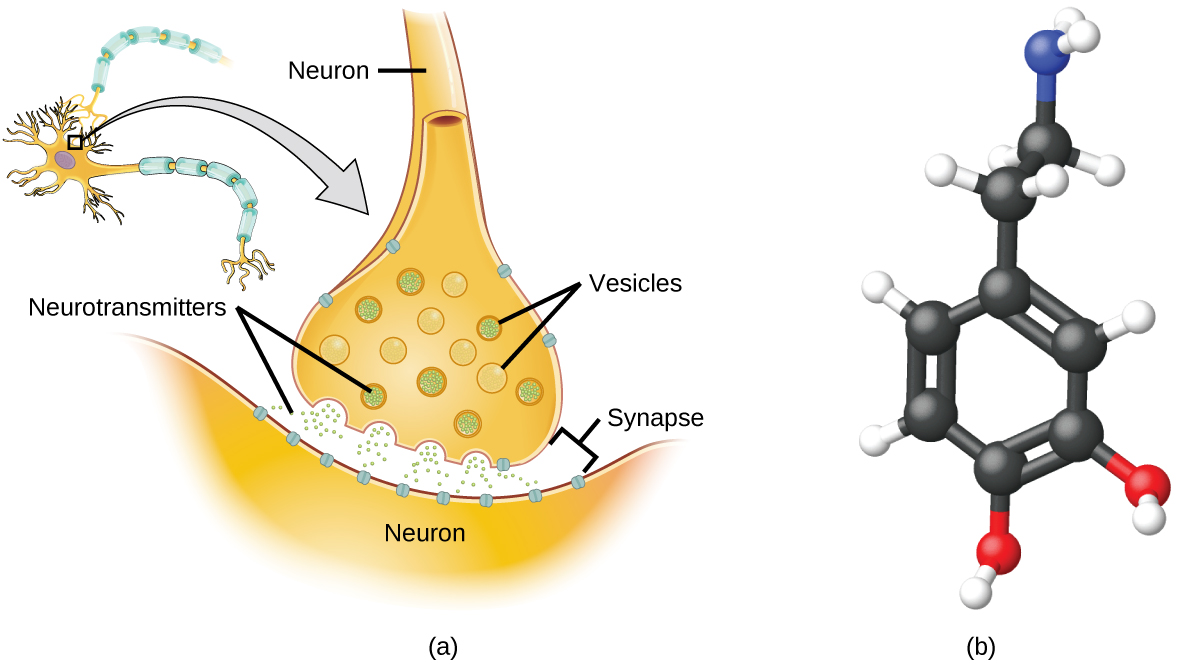
Two diagrams are shown. In the upper left corner of the left diagram, an oval with a darkened center that has five short, branching appendages and one long tail-like appendage is shown and connected by an arrow to another image. This image depicts a close-up view of the oval section and its interaction with the tail-like portion of a similar structure. The close up view is composed of a narrow tube labeled “neuron” leading down to a bulbous base that holds thirteen circles filled with small dots. These circles are labeled “vesicles.” The base of the bulbous structure is next to a curved object labeled “neuron” and very small dots are emerging from the bulb’s base and flowing toward the curved structure. The gap in between the two structures is labeled “synapse,” and the small dots are labeled “neurotransmitters.” The diagram on the right depicts a molecule composed of six black spheres connected by alternating double and single bonds in a hexagonal ring with other spheres attached to it. Three of the black spheres are connected to one smaller, white sphere each. Two of the black balls are connected to a smaller red sphere each. Each red sphere is connected to a smaller, white sphere. One black sphere is connected to another black sphere. It is connected to two smaller, white spheres and another black sphere. This second black sphere is connected to two smaller white spheres, and a slightly smaller blue sphere. The blue sphere is connected to two smaller, white spheres.
Figure 7.2g: (a) Chemical signals are transmitted from neurons to other cells by the release of neurotransmitter molecules into the small gaps (synapses) between the cells. (b) Dopamine, C8H11NO2, is a neurotransmitter involved in a number of neurological processes (credit: Chemistry (OpenStax), CC BY 4.0).

One important aspect of the complex processes related to dopamine signalling is the number of neurotransmitter molecules released during exocytosis. Since this number is a central factor in determining neurological response (and subsequent human thought and action), it is important to know how this number changes with certain controlled stimulations, such as the administration of drugs. It is also important to understand the mechanism responsible for any changes in the number of neurotransmitter molecules released—for example, some dysfunction in exocytosis, a change in the number of vesicles in the neuron, or a change in the number of neurotransmitter molecules in each vesicle.

Significant progress has been made recently in directly measuring the number of dopamine molecules stored in individual vesicles and the amount actually released when the vesicle undergoes exocytosis. Using miniaturized probes that can selectively detect dopamine molecules in very small amounts, scientists have determined that the vesicles of a certain type of mouse brain neuron contain an average of 30,000 dopamine molecules per vesicle (about 5 × 10−20 mol or 50 zmol). Analysis of these neurons from mice subjected to various drug therapies shows significant changes in the average number of dopamine molecules contained in individual vesicles, increasing or decreasing by up to three-fold, depending on the specific drug used. These studies also indicate that not all of the dopamine in a given vesicle is released during exocytosis, suggesting that it may be possible to regulate the fraction released using pharmaceutical therapies.[8]

Links to Interactive Learning Tools

Practice Molar Mass calculations from the Physics Classroom.

Practice Mole Conversions from the Physics Classroom.

Key Equations

[latex]n = \frac{m}{M}[/latex]

Number of atoms/ions/molecules = n x NA

Attribution & References

Except where otherwise noted, this page is adapted by Adrienne Richards from:

  1. 151.16 amu ; 151.16 g/mol ↵
  2. 310.18 amu ; 310.18 g/mol ↵
  3. 0.360 mol Be ↵
  4. 504.4 g Ar ↵
  5. 0.073 mol C12H22O11 ↵
  6. 14.2 g hydrazine ↵
  7. 4.586 x 1022 Au atoms ↵
  8. Omiatek, Donna M., Amanda J. Bressler, Ann-Sofie Cans, Anne M. Andrews, Michael L. Heien, and Andrew G. Ewing. “The Real Catecholamine Content of Secretory Vesicles in the CNS Revealed by Electrochemical Cytometry.” Scientific Report 3 (2013): 1447, accessed January 14, 2015, doi:10.1038/srep01447. ↵
definition

License

Icon for the Creative Commons Attribution 4.0 International License

Enhanced Introductory College Chemistry Copyright © 2023 by Gregory Anderson; Caryn Fahey; Jackie MacDonald; Adrienne Richards; Samantha Sullivan Sauer; J.R. van Haarlem; and David Wegman is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book