Solutions
Chapter 1 – Stoichiometry
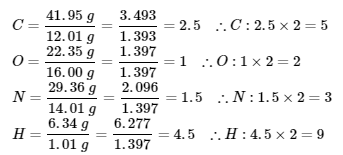
∴ the empirical formula of the unknown gas is C5O2N3H9
2. (1) Balancing: MnO4– (aq) → Mn2+ (aq)
MnO4– (aq) → Mn2+ (aq) + 4 H2O
MnO4– (aq) + 8 H+ → Mn2+ (aq) + 4 H2O
3 OH– + MnO4– (aq) + 8 H+ → Mn2+ (aq) + 4 H2O + 8 OH–
8 H2O + MnO4– (aq) → Mn2+ (aq) + 4 H2O + 8 OH–
4 H2O + MnO4– (aq) → Mn2+ (aq) + 8 OH–
4 H2O + MnO4– (aq) + 5 e– → Mn2+ (aq) + 8 OH– (x 28)
(2) Balancing C6H12O4 (aq) → 6 HCO3– (aq)
14 H2O + C6H12O4 (aq) → 6 HCO3– (aq)
14 H2O + C6H12O4 (aq) → 6 HCO3– (aq) + 34 H+
34 OH– + 14 H2O + C6H12O4 (aq) → 6 HCO3– (aq) + 34 H+ + 34 OH–
34 OH– + 14 H2O + C6H12O4 (aq) → 6 HCO3– (aq) + 34 H2O
34 OH– + C6H12O4 (aq) → 6 HCO3– (aq) + 20 H2O
34 OH– + C6H12O4 (aq) → 6 HCO3– (aq) + 20 H2O + 28 e– (x 5)
(3) Combine half equations for the final answer: 12 H2O + 28 MnO4– (aq) + 5 C6H12O4 (aq) 28 Mn2+ (aq) + 54 OH– + 30 HCO3– (aq)
3.

4.


5. Cl2 (g)
6. +2
7. (1) calculate the number of moles of H3PO4 that would be produced to determine the limiting reagent:
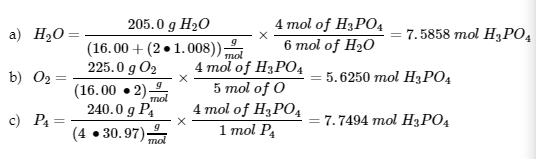
O2 is the limiting reagent
![]()
(2) The mass of the excess reagents that did not react:
Excess mass = (205.0 + 225.0 + 240.0) g – 551.2 g = 118.8 g
8. 28.6% by mass means there are 28.6 g C2H6O2 in 100 g of solution. Therefore, the mass of water in the solution is the difference between these values:
|
|
C2H6O2 |
H2O |
SOLUTION |
|
Mass (g) |
28.6 |
71.4 |
100 |
|
Molar Mass (g/mol) |
62.07 |
|
|
|
Mol |
0.461 |
|
|
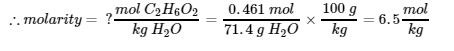
9.


10.
2 e– + Pb2+ (aq) → Pb (s)
2 OH– (aq) + CN– (aq) → CNO– (aq) +H2O (l) + 2 e-
____________________________________________________
CN– (aq) + 2 OH– (aq) + Pb2+ (aq) → CNO– (aq) + H2O (l) + Pb (s)
Reducing agent → CN– (aq)Oxidizing Agent → Pb2+ (aq)
11. NO3–
12.
Chapter 2 – Gases
- (1) Balanced chemical equation: C2H5OH (l) + 3 O2 (g) → 2 CO2 (g) + 3 H2O (l)
(2) Find the mass of CO2 (g):
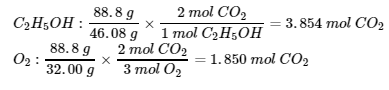
- O2 is the limiting reagent ∴ mass of CO2 = (1.850 mol)(44.01g/mol) = 81.4 g
(3)

(4)

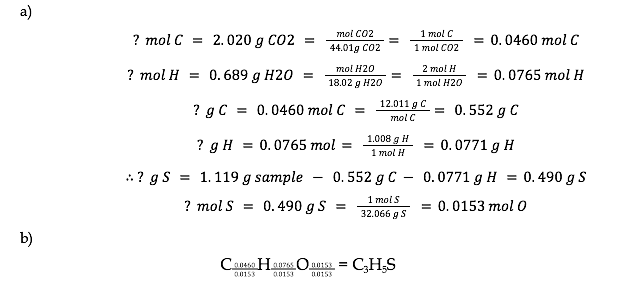
2. (1)
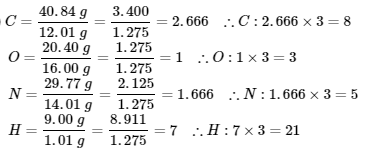
∴ the empirical formula of the unknown gas is C8O3N5H21
(2)
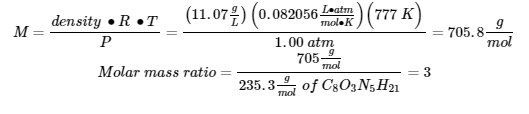
∴ the molecular formula of the unknown gas is C24O9N15H63
3.


4. (a)
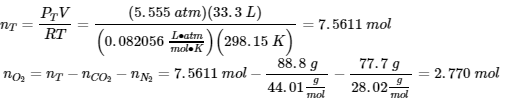
? mass O2 = (2.770 mol)(32.00 g/mol) = 88.7 g
(b)

5. (1)
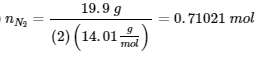
Find the initial temperature:

6. 0.020 mol/hr
7. False
8. (a)
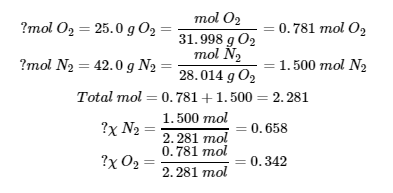
(b)

9.

10.
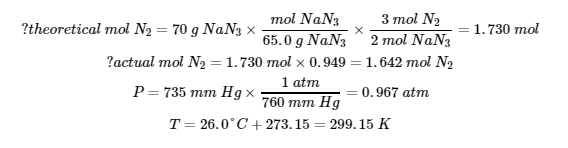
Chapter 3 – Thermochemistry
- (1) calculate the value of q for the combustion of 1.22 g of C6H10O(l) at a constant volume (which means that q = ∆U)
qreaction = ΔU = – qwater – qcal
qreaction = – mH2O∙c∙∆TH2O-(Ccal∙∆Tcal)
qreaction = -(2725 g)(4.188 J/g∙K)(2.75 K) – (3500 J/K)(2.75 K)
qreaction = – 40988 J
qreaction = – 40.988 kJ
For one mole; there is 98.14 g
x = ΔU = – 3297 kJ
(2) now, we will find Q, W, ∆H and ∆U at constant pressure. But ∆U is always -3297 kJ
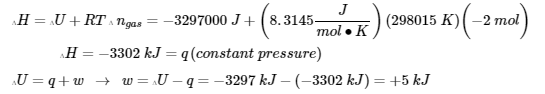
2. (a)

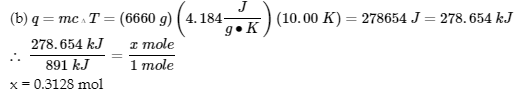

3. The heat that leaves the iron enters the water and the container:

4. (1) Use Hess’ Law
C (graphite) + O2 (g) → CO2 (g) ΔH = – 393.5 kJ
2 H2 (g) + O2 (g) → 2 H2O (l) ΔH = 2(- 285.8 kJ) = – 571.6 kJ
CO2 (g) + 2 H2O (l) → CH3OH (l) + 32 O2 (g) ΔH = -(- 726.4 kJ) = +726.4 kJ
CH3OH (l) → CH3OH (g) ΔH= + 37.4 kJ
C (graphite) + 2 H2 (g) + 12 O2 (g) → CH3OH (g) ΔH = -201.3 kJ
(2)

5.
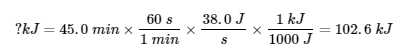
Technically, the sign here should be negative since heat is leaving, but since this is already acknowledged in the question, it’s not needed.
7. (a)
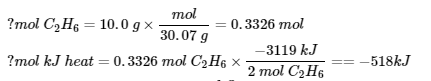
(b)
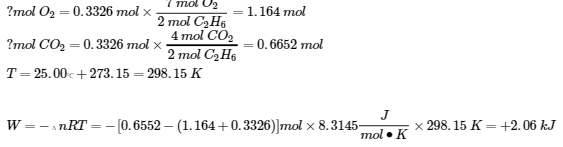
8. 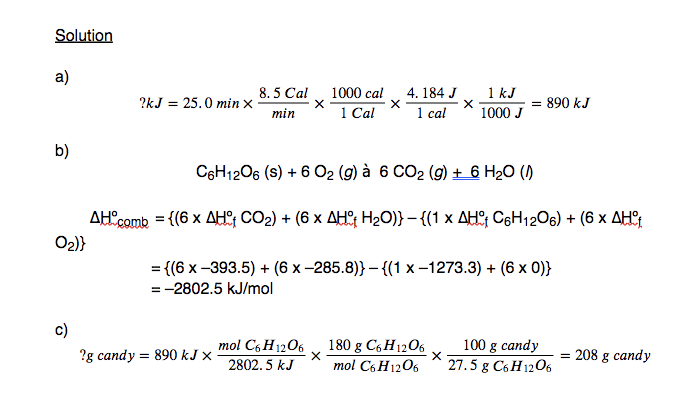
9. 
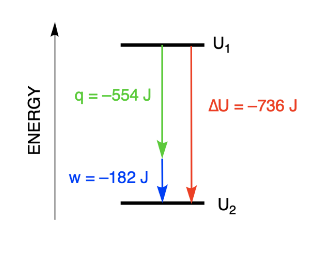
Chapter 4 – Chemical Equilibrium
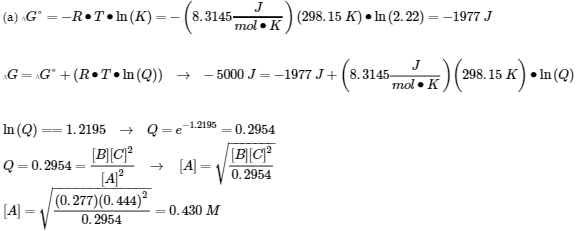
(b)
|
|
2 A (g) |
2 B (g) + |
C (g) |
|
I |
4.00 atm |
2.00 atm |
|
|
C |
-2x |
+ 2x |
+x |
|
E |
4.00 – 2x |
2.00 + 2x |
x |
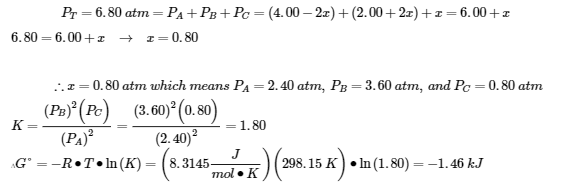
2.
![]()
|
|
A (aq) + |
B (aq) ⇌ |
2 C (aq) |
|
I |
0.322 M |
0.244 M |
0.455 M |
|
C |
-x |
-x |
+2x |
|
E |
0.322 – x |
0.244 – x |
0.455 + 2x |
(note that x is found using the quadratic formula and x = -0.348 is impossible)
3. Note that the molar mass of AgNO3 is 169.87 g/mol
![]()
|
|
Ag+ (aq) + |
2 CN– (aq) ⇌ |
Ag(CN)2– (aq) |
|
I |
0.03903 |
0.800 |
|
|
C |
-0.03903 |
-20.03903 |
+0.03903 |
|
E |
|
0.72194 |
0.03903 |
Note: a small amount of Ag(CN)2– will react to regenerate Ag+ … the concentrations of CN– and Ag(CN)2– are not affected.
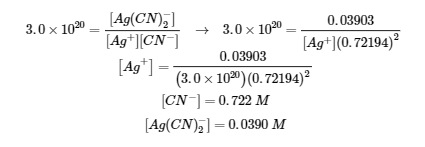
4. (a)
![]()
|
|
A (g) |
2 B (g) |
2 C (g) |
|
I |
0.500 |
0.500 |
0 |
|
C |
-0.245 |
-0.245 |
+0.489 |
|
E |
0.255 |
0.011 |
0.489 |
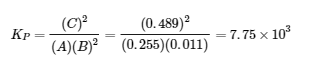
(b)
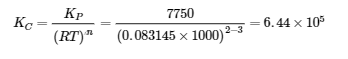
5. Ptotal = 20.0 bar = PCH4 + PCO2. Since nCH4 = nCO2 (equimolar), that means each gas has an initial partial pressure of 10.0 bar.
|
|
CH4 (g) |
CO2 (g) |
2 CO (g) |
2 H2 (g) |
|
I |
10.0 |
10.0 |
0 |
0 |
|
C |
-x |
-x |
+2x |
+2x |
|
E |
0.246 |
0.2 |
19.6 |
19.6 |
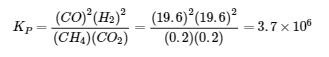
6. 0.83
Divide Equation 1’s equilibrium constant by 2 and multiple Equation 2’s equilibrium constant by -1 (as you have to flip it); Add modified equilibrium constants to get 0.83.
Chapter 5 -Acid/Base Equilibria
- NH4+ (aq) ⇌ NH3 (aq) + H+ (aq)
E: 0.333 – x 0.333 x x
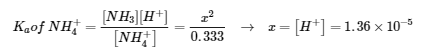
pH = -log(1.36 x 10-5) = 4.87
2. (a)
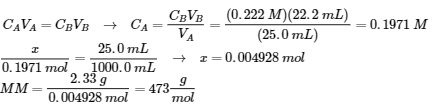
(b) HA (aq) ⇌ H+ (aq) + A– (aq)
E: 0.1971 – x x x
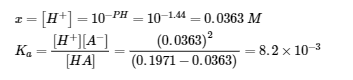
(c) A– (aq) + H2O (l) ⇌ HA (aq) + OH– (aq)
E: 2.000 – x 2.000 x x
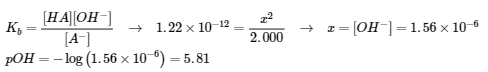
pH = 8.19
3. (a)
|
|
2 A (aq) ⇌ |
B (aq) + |
C (aq) |
|
I |
0.444 |
0.555 |
0.666 |
|
C |
-2x |
+x |
+x |
|
E |
0.444 – 2x |
0.555 + x |
0.666 + x |
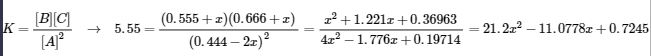
21.2x2 – 11.0778x + 0.7245 = 0 → x = 0.4459 and 0.0765 (Note: use quadratic formula to find values for x and x = 0.4459 is impossible so we use 0.0765)
[A] = 0.44 – 2(0.0765) = 0.291 M
(b)
 ∴ pOH = 2.29 and pH = 11.71
∴ pOH = 2.29 and pH = 11.71
4.
pOH = 14 – pH – 3.45
[OH-] = 10-3.45 = 3.55 x 10-4 M
Let B represent the base, N(CH3)3,
|
|
B |
H2O |
OH– |
HB+ |
|
I |
[B] |
– |
0 |
0 |
|
C |
-x |
– |
+x |
+x |
|
E |
[B] – x |
– |
x |
X |
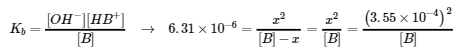
[B] = 0.0200 M
Check: ![]()
5. (a) Initial pH
|
|
HA |
H2O |
H3O+ |
A– |
|
I |
0.090 |
– |
0 |
0 |
|
C |
-x |
– |
+x |
+x |
|
E |
0.090 – x |
– |
x |
X |
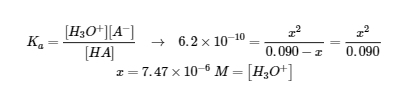
Check: ![]()
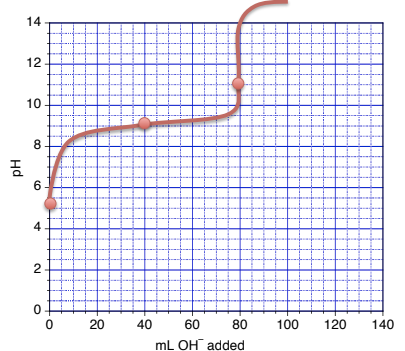
(b) At half equivalence point: pH = pKa = -log(6.2 x 10-10) = 9.21 (after 40 mL added)
(c) At the equivalence point
mol HA = mol OH- added = 0.0072 mol (this corresponds to adding 80.0 mL of base)
new [A-] = 0.0072 mol/(0.080 L + 0.080 L) = 0.0450 M
OCl– is a conjugate base of a weak acid, so it hydrolyzes:
|
|
A– |
H2O |
HA |
OH– |
|
I |
0.045 |
– |
0 |
0 |
|
C |
-x |
– |
+x |
+x |
|
E |
0.045 – x |
– |
x |
x |
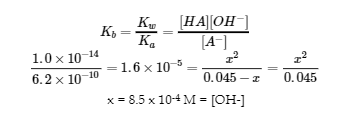
x = 8.5 x 10-4 M = [OH-]
pOH = -log(8.5 x 10-4) = 3.07
pH = 14 – 3.07 = 10.93
(d)
Chapter 6 – Ionic Equilibria in Aqueous Systems
- (a) The molar mass of Mg(PO4)2 is 262.86 g/mol
|
|
Mg(PO4)2 (s) ⇌ |
3 Mg+ (aq) + |
2 PO43- (aq) |
|
I |
|
|
|
|
C |
|
+ 3x |
+ 2x |
|
E |
|
3x |
2x |
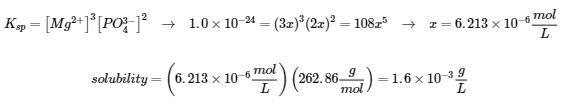
(b)
|
|
Mg(PO4)2 (s) ⇌ |
3 Mg+ (aq) + |
2 PO43- (aq) |
|
I |
|
0.30 |
|
|
C |
|
+ 3x |
+ 2x |
|
E |
|
0.30 + 3x 0.30 |
2x |
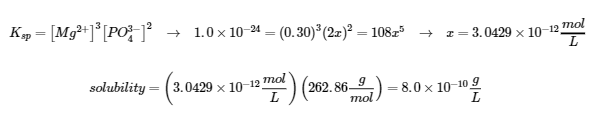
2. (a)
|
|
NH3 (aq) + |
H+ (aq) ⇌
|
NH4+ (aq) |
|
I |
0.7103 |
0.1701 |
|
|
C |
– 0.1701 |
– 0.1701 |
+ 0.1701 |
|
E |
0.5402 |
|
0.1701 |
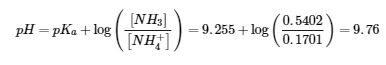
(b) 1.00 g of NaOH (0.0250 mol) consumes 0.0250 mol of NH4+ (aq) and produces 0.0250 mol of NH3 (aq)
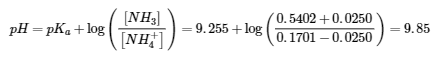
(c) 1.00 g of HCl (0.0274 mol) consumes 0.0274 mol of NH3 (aq)and produces 0.0274 mol of NH4+ (aq)
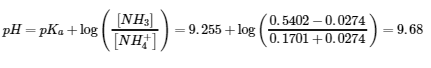
3. The Ba(OH)2 has 2 groups of OH–, so CAVA = 2 CBVB
![]()
- At the equivalence point, the volume is (70.4 mL + 28.0 mL) = 98.4 mL
- All of the acetic acid is converted to CH3COO–; a weak base:
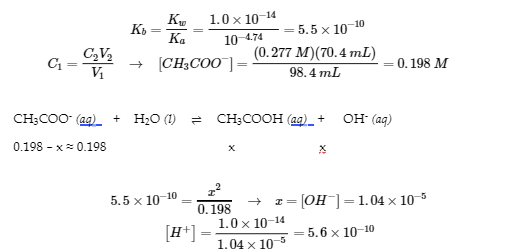
pH = 9.02
4.
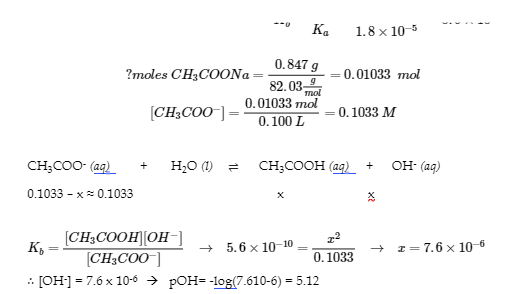
pH = 14 – pOH → pH=8.88
5. (a)
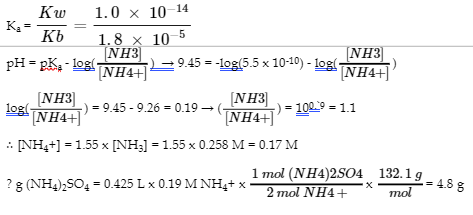
(b)
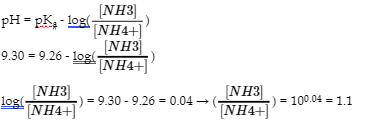
To lower pH to 9.30, we need to add acid. But how much?
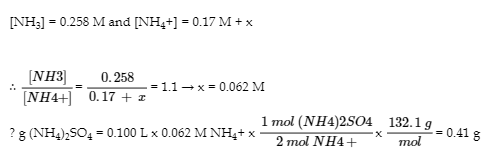
Amount: 0.41 g
6. (a) PbI2
(b)
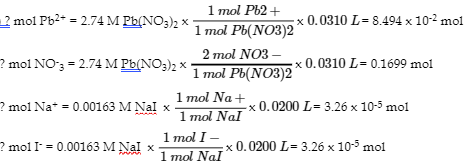
|
|
Pb2+ |
I- |
PbI2 (s) |
|
B |
8.494 x 10-2 mol |
|
0 |
|
A |
|
3.26 x 10-5 mol |
|
|
M |
-0.5 x 3.26 x 10-5 mol |
-3.26 x 10-5 mol |
+0.5 x 3.26 x 10-5 mol |
|
A |
8.494 x 10-2 mol |
0 |
1.63 x 10-5 mol |
1.63 x 10-5 mol of PbI2 precipitates and total volume is 20.0 mL + 30.0 mL = 51.0 mL
? [Pb2+] = 8.494 x 10-2 mol/0.0510 L = 1.665 M
? [NO–3] = 0.1699 mol/0.0510 L = 3.33 M
? [Na+] = 3.26 x 10-5 mol/0.0510 L = 6.39 x 10-4 M
? [I-] = 0 mol/0.0510 L = 0 M
7. Circled → Ca(CN)2 and LiF
Underlined → KCl and CuNO3

