3.2 – Types of Energy

Thermochemistry is a branch of chemical thermodynamics, the science that deals with the relationships between heat, work, and other forms of energy in the context of chemical and physical processes. As we concentrate on thermochemistry in this chapter, we need to consider some widely used concepts of thermodynamics.

Substances act as reservoirs of energy, meaning that energy can be added to them or removed from them. Energy is stored in a substance when the kinetic energy of its atoms or molecules is raised. The greater kinetic energy may be in the form of increased translations (travel or straight-line motions), vibrations, or rotations of the atoms or molecules. When thermal energy is lost, the intensities of these motions decrease and the kinetic energy falls. The total of all possible kinds of energy present in a substance is called the internal energy (U), sometimes symbolized as E.

Internal energy

The internal energy of a system is identified with the random, disordered motion of molecules; the total (internal) energy in a system includes potential and kinetic energy. This is in contrast to external energy which is a function of the sample with respect to the outside environment (e.g. kinetic energy if the sample is moving or potential energy if the sample is at a height from the ground etc). The symbol for Internal Energy Change is ΔU and may be calculated using the following equation where U₁ is the initial internal energy of the system and U₂ is the system’s final internal energy:

ΔU = U₂ – U₁

Heat

Thermal energy is the kinetic energy associated with the random motion of atoms and molecules. Temperature is a quantitative measure of “hot” or “cold.” When the atoms and molecules in an object are moving or vibrating more quickly, they have a higher average kinetic energy (E_k), and we say that the object is “hot.” When the atoms and molecules are moving more slowly, they have lower E_k, and we say that the object is “cold” (Figure 3.2.1.). Assuming that no chemical reaction or phase change (such as melting or vaporizing) occurs, increasing the amount of thermal energy in a sample of matter will cause its temperature to increase. And, assuming that no chemical reaction or phase change (such as condensation or freezing) occurs, decreasing the amount of thermal energy in a sample of matter will cause its temperature to decrease.

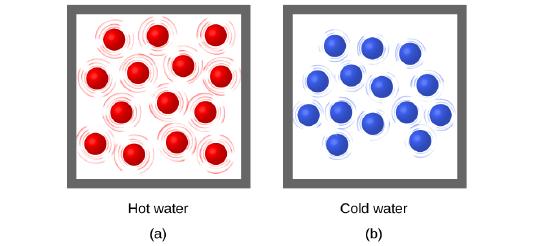
Figure 3.2.1. (a) The molecules in a sample of hot water move more rapidly than (b) those in a sample of cold water.

Heat (q) is the transfer of thermal energy between two bodies at different temperatures. Heat flow (a redundant term, but one commonly used) increases the thermal energy of one body and decreases the thermal energy of the other. Suppose we initially have a high temperature (and high thermal energy) substance (H) and a low temperature (and low thermal energy) substance (L). The atoms and molecules in H have a higher average E_k than those in L. If we place substance H in contact with substance L, the thermal energy will flow spontaneously from substance H to substance L. The temperature of substance H will decrease, as will the average E_k of its molecules; the temperature of substance L will increase, along with the average E_k of its molecules. Heat flow will continue until the two substances are at the same temperature (Figure 3.2.2.).

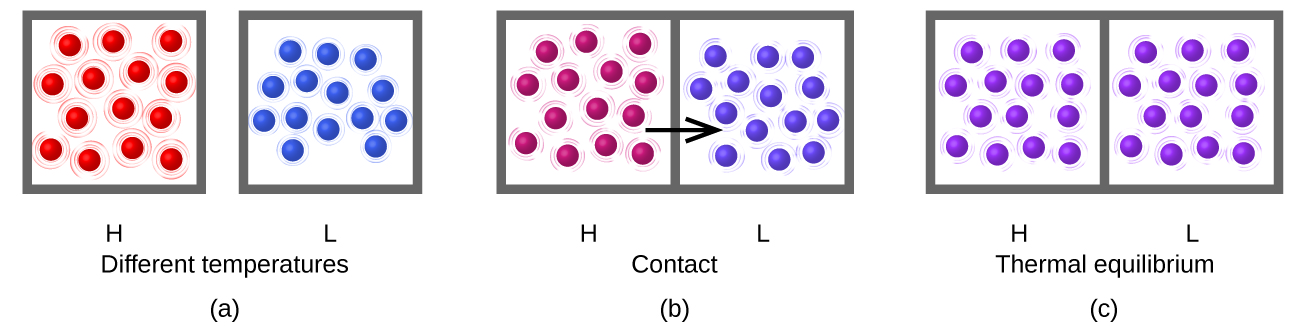
Figure 3.2.2. (a) Substances H and L are initially at different temperatures, and their atoms have different average kinetic energies. (b) When they are put into contact with each other, collisions between the molecules result in the transfer of kinetic (thermal) energy from the hotter to the cooler matter. (c) The two objects reach “thermal equilibrium” when both substances are at the same temperature, and their molecules have the same average kinetic energy.

Matter undergoing chemical reactions and physical changes can release or absorb heat. A change that releases heat is called an exothermic process. For example, the combustion reaction that occurs when using an oxyacetylene torch is an exothermic process—this process also releases energy in the form of light as evidenced by the torch’s flame (Figure 3.2.3. a). A reaction or change that absorbs heat is an endothermic process. A cold pack used to treat muscle strains provides an example of an endothermic process. When the substances in the cold pack (water and ammonium nitrate) are brought together, the resulting process absorbs heat, leading to the sensation of cold.

Figure 3.2.3. (a) An oxyacetylene torch produces heat by the combustion of acetylene and oxygen. The energy released by this exothermic reaction heats and then melts the metal being cut. The sparks are tiny bits of the molten metal flying away. (b) A cold pack uses an endothermic process to create the sensation of cold. (credit a: modification of work by “Skatebiker”/Wikimedia commons).

Heat Can do More than Increase Temperature

Most substances expand as their temperature increases and contract as their temperature decreases. This property can be used to measure temperature changes, as shown in Figure 3.2.4. The operation of many thermometers depends on the expansion and contraction of substances in response to temperature changes.

Figure 3.2.4. (a) In an alcohol or mercury thermometer, the liquid (dyed red for visibility) expands when heated and contracts when cooled, much more so than the glass tube that contains the liquid. (b) In a bimetallic thermometer, two different metals (such as brass and steel) form a two-layered strip. When heated or cooled, one of the metals (brass) expands or contracts more than the other metal (steel), causing the strip to coil or uncoil. Both types of thermometers have a calibrated scale that indicates the temperature. (credit a: modification of work by “dwstucke”/Flickr). (c) The demonstration allows one to view the effects of heating and cooling a coiled bimetallic strip. A bimetallic coil from a thermometer reacts to the heat from a lighter, by uncoiling and then coiling back up when the lighter is removed. Animation used with permission from Hustvedt (via Wikipedia)

Direction of Heat Flow: Endothermic vs. Exothermic Processes

The reaction of powdered aluminum with iron(III) oxide, known as the thermite reaction, generates an enormous amount of heat—enough, in fact, to melt steel. The balanced chemical equation for the reaction is as follows:

2 Al (s) + Fe₂O₃ (s)  →  2 Fe (s)  + Al₂O₃ (s)

We can also write this chemical equation as:

2 Al (s) + Fe₂O₃ (s) → 2 Fe (s) + Al₂O₃ (s) + heat

to indicate that heat is one of the products. Chemical equations in which heat is shown as either a reactant or a product are called thermochemical equations. In this reaction, the system consists of aluminum, iron, and oxygen atoms; everything else, including the container, makes up the surroundings. During the reaction, so much heat is produced that initially, the iron is in its liquefied form, Fe (l ). Eventually, the system cools; the iron solidifies as heat is transferred to the surroundings. A process in which heat (q) is transferred from a system to its surroundings is described as exothermic. By convention, q < 0 for an exothermic reaction. Check out this video to see the above reaction in action.

When you hold an ice cube in your hand, heat from the surroundings (including your hand) is transferred to the system (the ice), causing the ice to melt and your hand to become cold. We can describe this process by the following thermochemical equation:

heat + H₂O (s)  →  H₂O (l)

When heat is transferred to a system from its surroundings, the process is endothermic. By convention, q > 0 for an endothermic reaction.

In summary, sign conventions indicate the direction of heat flow: q < 0 for an exothermic reaction and q > 0 for an endothermic reaction.

Example 3.2.1 – Exothermic vs. Endothermic Reactions

                 Decide whether the following are endothermic or exothermic processes

      a. water evaporates off a shower door

      b. an acid tablet being added to a pool and the surrounding water heats up

      c. NH₄Cl is dissolved in water and the solution cools

      d. the burning of a log in a campfire

Solution

      a. Endothermic

      b. Exothermic

      c. Endothermic

      d. Exothermic

Technically, it is poor form to have heat in the chemical reaction like in the equations depicted above since it is not a true species in the reaction. However, this is a convenient approach to represent exothermic and endothermic behavior and is commonly used by chemists.

Work

In chemistry, work is often defined in terms of a change in volume against pressure. (Pressure is force divided by area, so convince yourself that P x V has the same units as F x d.) For instance, atmospheric pressure is nearly constant at around 1 bar. If you have a sample of gas at higher pressure, and you let it come to mechanical equilibrium with the atmosphere, it will expand to some new volume. The work done by expanding against atmospheric pressure is (1 bar)(ΔV), where ΔV is (final volume – initial volume). In general, the work done by gases expanding or contracting is called PV work, and is expressed:

w = – PΔV = -P(V₂ – V₁) 

where P is the constant external pressure (sometimes shown as P_ext) and ΔV  is the change in volume of the system. The negative sign associated with PV work done indicates that the system loses energy when the volume increases. If the volume increases at constant pressure (ΔV > 0), the work done by the system is negative, indicating that a system has lost energy by performing work on its surroundings. Conversely, if the volume decreases (ΔV < 0), the work done by the system is positive, which means that the surroundings have performed work on the system, thereby increasing its energy.

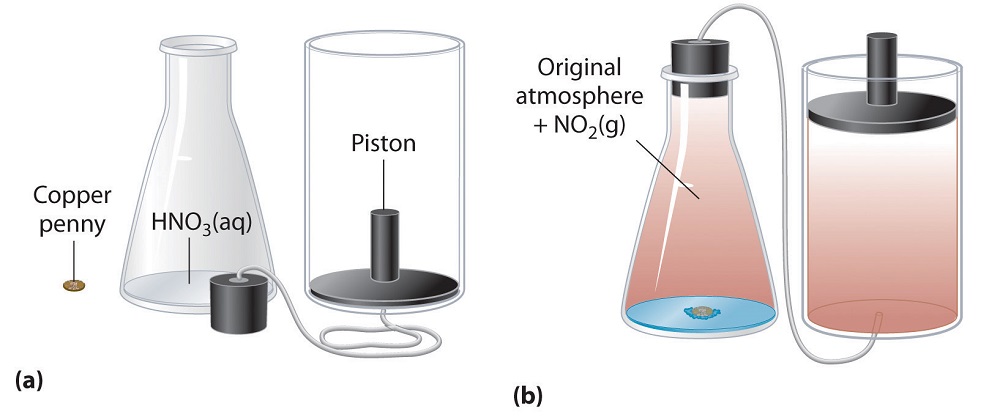
Figure 3.2.5. An Example of Work Performed by a Reaction Carried Out at Constant Pressure. (a) Initially, the system (a copper penny and concentrated nitric acid) is at atmospheric pressure. (b) When the penny is added to the nitric acid, the volume of NO₂ gas that is formed causes the piston to move upward to maintain the system at atmospheric pressure. In doing so, the system is performing work on its surroundings.

Chemical reactions can carry out work by electrochemistry (this involves redox reactions and will be covered in future CHM courses), and the pressure-volume work of gases.

Example 3.2.2 – Work Calculations with Gases

What is the work performed by a gas if it expands from 3.44 L to 6.19 L against a constant external pressure of 1.26 atm? Express the final answer in joules.

Solution

First, we need to determine the change in volume, ΔV. A change is always the final value minus the initial value:

ΔV = V_final – V_initial

ΔV = 6.19 L – 3.44 L

ΔV = 2.75 L

 In order to find the work in units of joules, the volume change will need to be converted to the appropriate SI units (m3), and the external pressure will need to be expressed in Pascals (Pa): 

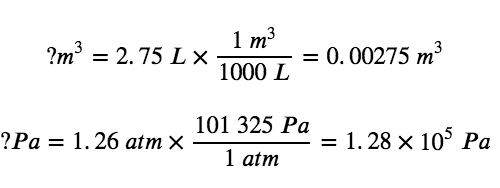
Now we can use the definition of work to determine the work done (note again that, according to SI units, 1 Pa•m³ = 1 J):

The negative sign indicates that this was an expansion of a gas: the system (the gas) did work on its surroundings (the external pressure) to increase its volume. The internal energy of the system must therefore be decreasing in order to carry out this work. 

Check Your Learning 3.2.1 – Work Calculations with Gases

What is the work performed when a gas expands from 0.66 L to 1.33 L against an external pressure of 0.775 atm?

Answer

-53 J

Heat and work are the ways that energy can move between objects. When you think about the molecules, the difference between work and heat is very simple. Work involves an orderly motion of molecules, like all the molecules in an object moving the same direction. Heat involves disorderly or random motions of molecules.

Questions

★Questions

1. A system of molecules has an original internal energy of 8700000 J. You cooled this system by 99 K and its internal energy is now 4501 kJ. Calculate the change in internal energy (ΔU).
2. You allow two iron cubes to come into contact. One cube is at 800 K and the other is at 323.15°C. Predict the temperature of these two cubes once they reach thermal equilibrium. State your answer in Kelvin.
3. Calculate how many calories are in 71 kJ.
4. Classify each reaction as exothermic or endothermic:

C₆H₁₂O₆ (s) + 6 O₂ (g)  →  6 CO₂ (g) + 6 H₂O (l) + heat

         a. Ice melts into water

         b. TNT explodes

         c. Nuclear fission breaks uranium atoms into atoms with smaller nuclei

★★Questions

   5. You have a balloon initially filled with 400 mL of air. What is the final volume of    the balloon if you do -885.13 J of work to expand it? Atmospheric pressure is 1.12        atm.

Answers

1. – 4199 kJ
2. 698.15 K
3. 16.96 kilocalories
4. (a) Exothermic, (b) Endothermic, (c) Exothermic, (d) Exothermic
5. 1190.29 mL