1.3 – Reaction Stoichiometry
The Stoichiometry of Balanced Chemical Equations
A balanced chemical equation provides a great deal of information in a very succinct format. Chemical formulas provide the identities of the reactants and products involved in the chemical change, allowing the classification of the reaction. Coefficients provide the relative numbers of these chemical species, allowing a quantitative assessment of the relationships between the amounts of substances consumed and produced by the reaction. These quantitative relationships are known as the reaction’s stoichiometry, a term derived from the Greek words stoicheion (meaning “element”) and metron (meaning “measure”). In this module, the use of balanced chemical equations for various stoichiometric applications is explored.
The general approach to using stoichiometric relationships is similar in concept to the way people go about many common activities. Food preparation, for example, offers an appropriate comparison. A recipe for making eight pancakes calls for 1 cup pancake mix, ¾ cup milk, and one egg. The “equation” representing the preparation of pancakes per this recipe is:
1 cup mix + ¾ cup milk + 1 egg → 8 pancakes
If two dozen pancakes are needed for a big family breakfast, the ingredient amounts must be increased proportionally according to the amounts given in the recipe. For example, the number of eggs required to make 24 pancakes is:
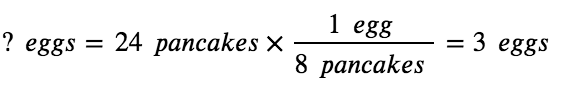
Balanced chemical equations are used in much the same fashion to determine the amount of one reactant required to react with a given amount of another reactant, or to yield a given amount of product, and so forth. The coefficients in the balanced equation are used to derive stoichiometric factors that permit the computation of the desired quantity. To illustrate this idea, consider the production of ammonia by the reaction of hydrogen and nitrogen:
N2 (g) + 3H2 (g) → 2NH3 (g)
This equation shows ammonia molecules are produced from hydrogen molecules in a 2:3 ratio, and stoichiometric factors may be derived using any amount (number) unit:
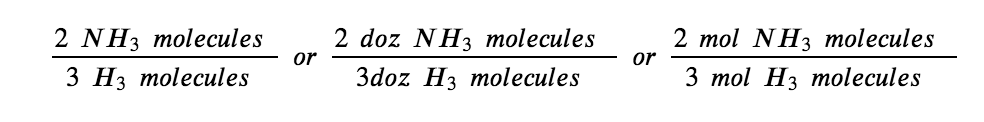
These stoichiometric factors can be used to compute the number of ammonia molecules produced from a given number of hydrogen molecules, or the number of hydrogen molecules required to produce a given number of ammonia molecules. Similar factors may be derived for any pair of substances in any chemical equation.
Example 1.3.1 – Moles of Reactant Required in a Reaction
How many moles of molecular iodine, I2 , are required to react with 0.429 mol of Al according to the following equation (see Figure 1.3.1)
![]()

Figure 1.3.1. Aluminum and iodine react to produce aluminum iodide. The heat of the reaction vaporizes some of the solid iodine as a purple vapour. (credit: modification of work by Mark Ott)
Solution
Referring to the balanced chemical equation, the stoichiometric factor relating the two substances of interest is 3 mol I2, 2 mol Al. The molar amount of iodine is derived by multiplying the provided molar amount of aluminum by this factor:

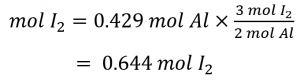
Check Your Learning 1.3.1 – Moles of Reactant Required in a Reaction
How many moles of Ca(OH)2 are required to react with 1.36 mol of H3PO4 to produce Ca3(PO4)2 according to the equation 3 Ca(OH)2 + 2 H3PO4 ⟶ Ca3(PO4)2 + 6 H2O?
Answer
n = 2.04 mol
Example 1.3.2 – Number of Product Molecules Generated by a Reaction
How many carbon dioxide molecules are produced when 0.75 mol of propane is combusted according to this equation?
C3H8 + 5 O2 → 3 CO2 + 4 H2O
Solution
The approach here is the same as for the previous example, though the absolute number of molecules is requested, not the number of moles of molecules. This will simply require the use of the moles-to-numbers conversion factor, Avogadro’s number.
The balanced equation shows that carbon dioxide is produced from propane in a 3:1 ratio:
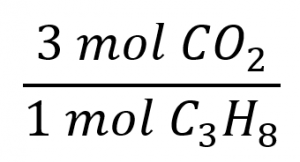
Using this stoichiometric factor, the provided molar amount of propane, and Avogadro’s number,

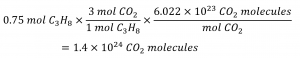
Check Your Learning 1.3.2 – Number of Product Molecules Generated by a
Reaction
How many NH3 molecules are produced by the reaction of 4.0 mol of Ca(OH)2 according to the following equation:
(NH4)2SO4 + Ca(OH)2 → 2 NH3 + CaSO4 + 2 H2O
Answer
4.8 × 1024 NH3 molecules
These examples illustrate the ease with which the amounts of substances involved in a chemical reaction of known stoichiometry may be related. Directly measuring numbers of atoms and molecules is, however, not an easy task, and the practical application of stoichiometry requires that we use the more readily measured property of mass.
Example 1.3.3 – Relating Masses of Reactants and Products
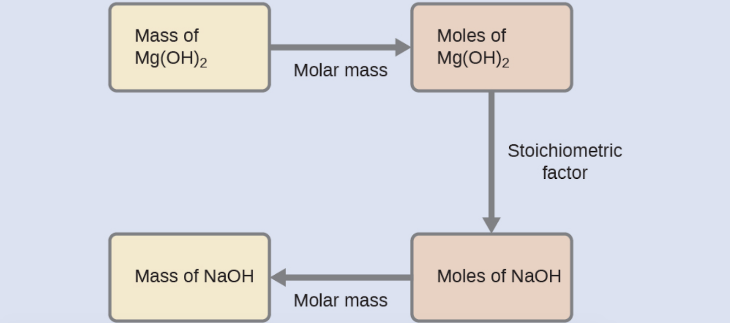
What mass of sodium hydroxide, NaOH, would be required to produce 16 g of the antacid milk of magnesia (magnesium hydroxide, Mg(OH)2 ) by the following reaction?
MgCl2 (aq) + 2 NaOH(aq) → Mg(OH)2 (s) + 2 NaCl (aq)
Solution
We must derive an appropriate stoichiometric factor from the balanced chemical equation and use it to relate the amounts of the two substances of interest. In this case, however, masses (not molar amounts) are provided and requested, so additional steps of the sort learned in the previous chapter are required. The calculations required are outlined in the following flow chart:

![]()
Check Your Learning 1.3.3 – Relating Masses of Reactants and Products
What mass of gallium oxide, Ga2O3, can be prepared from 29.0 g of gallium metal? The equation for the reaction is 4 Ga + 3 O2 ⟶ 2 Ga2O3.
Answer
m = 39.0 g
Example 1.3.4 – Relating Masses of Reactants
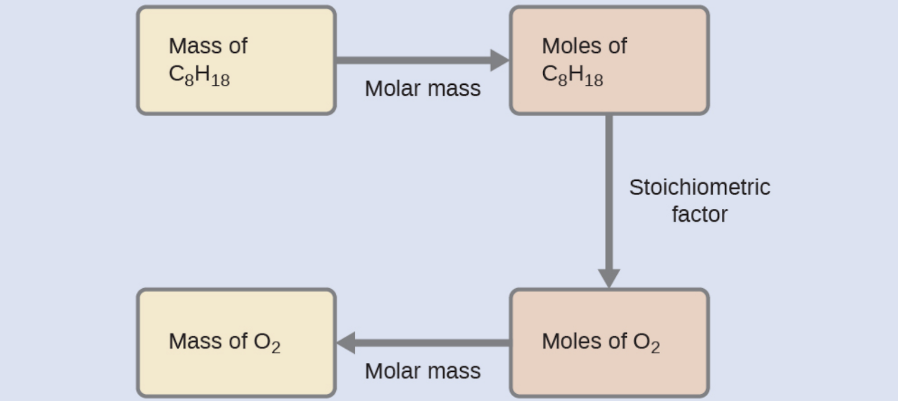
What mass of oxygen gas, O2, from the air is consumed in the combustion of 702 g of octane, C8H18, one of the principal components of gasoline?
2 C8H18 + 25 O2 → 16 CO2 + 18 H2O
Solution
The approach required here is the same as for the previous example, differing only in that the provided and requested masses are both for reactant species.
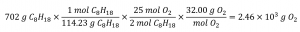
Check Your Learning 1.3.4 – Relating Masses of Reactants
What mass of CO is required to react with 25.13 g of Fe2O3 according to the following equation?
Fe2O3 + 3 CO ⟶ 2 Fe + 3 CO2
Answer
m = 13.22 g
These examples illustrate just a few instances of reaction stoichiometry calculations. Numerous variations on the beginning and ending computational steps are possible depending upon what particular quantities are provided and sought (volumes, solution concentrations, and so forth). Regardless of the details, all these calculations share a common essential component: the use of stoichiometric factors derived from balanced chemical equations. Figure 1.3.2 provides a general outline of the various computational steps associated with many reaction stoichiometry calculations.
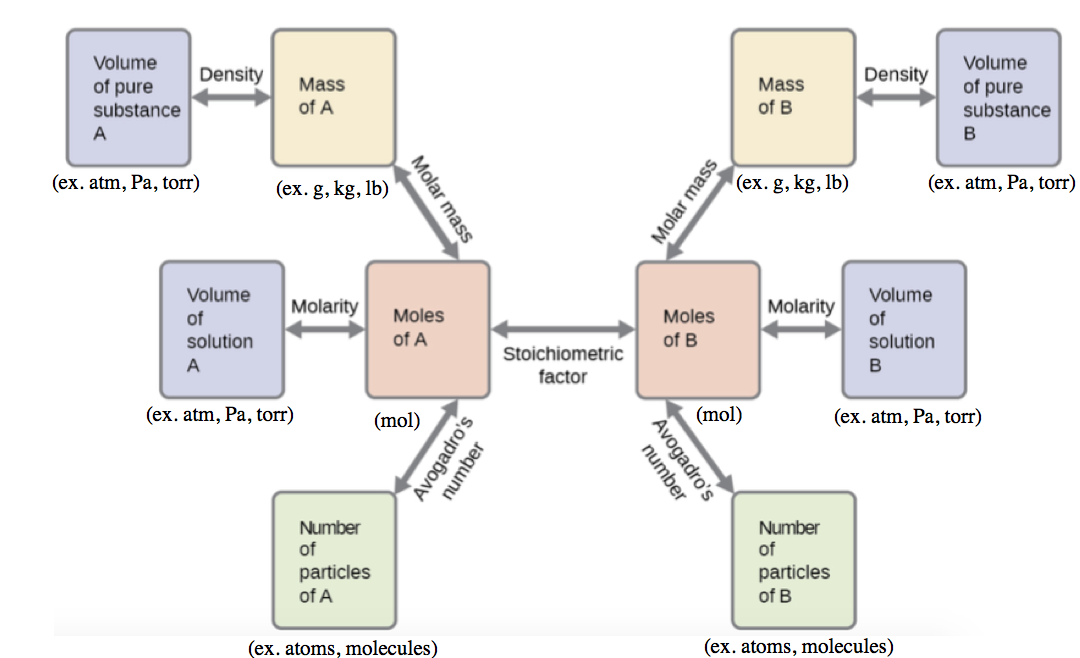 Figure 1.3.2. The flow chart depicts the various computational steps involved in most reaction stoichiometry calculations.
Figure 1.3.2. The flow chart depicts the various computational steps involved in most reaction stoichiometry calculations.
Limiting Reactant
Consider another food analogy, making grilled cheese sandwiches (Figure 1.3.3):
1 slice of cheese + 2 slices of bread → 1 sandwich
Stoichiometric amounts of sandwich ingredients for this recipe are bread and cheese slices in a 2:1 ratio. Provided with 28 slices of bread and 11 slices of cheese, one may prepare 11 sandwiches per the provided recipe, using all the provided cheese and having six slices of bread leftover. In this scenario, the number of sandwiches prepared has been limited by the number of cheese slices, and the bread slices have been provided in excess.
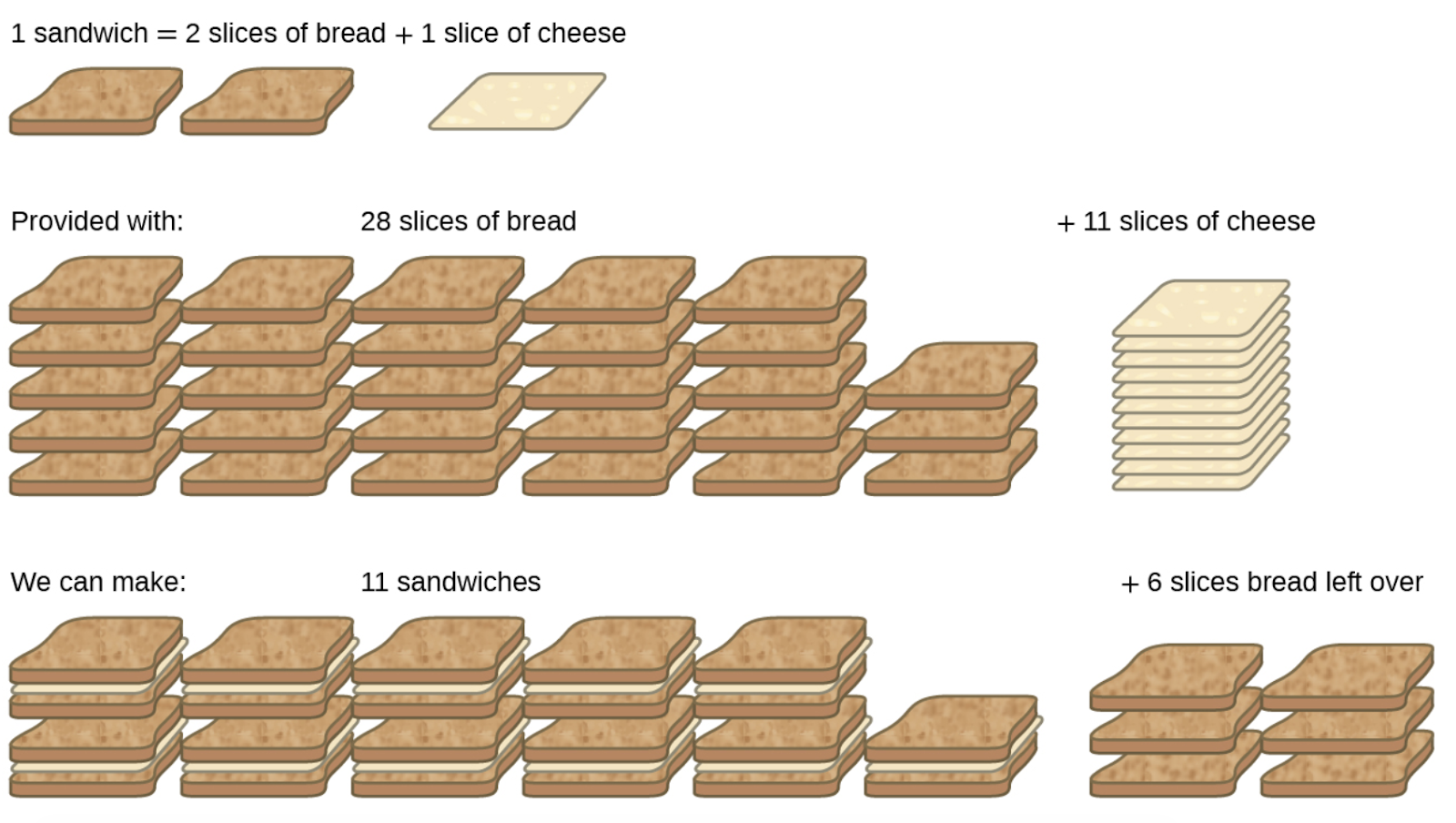 Figure 1.3.3. Sandwich making can illustrate the concepts of limiting and excess reactants.
Figure 1.3.3. Sandwich making can illustrate the concepts of limiting and excess reactants.
Consider this concept now with regard to a chemical process, the reaction of hydrogen with chlorine to yield hydrogen chloride:
H2 (g) + Cl2 (g) → 2 HCl (g)
The balanced equation shows the hydrogen and chlorine react in a 1:1 stoichiometric ratio. If these reactants are provided in any other amounts, one of the reactants will nearly always be entirely consumed, thus limiting the amount of product that may be generated. This substance is the limiting reactant, and the other substance is the excess reactant. Identifying the limiting and excess reactants for a given situation requires computing the molar amounts of each reactant provided and comparing them to the stoichiometric amounts represented in the balanced chemical equation. For example, imagine combining 3 moles of H2 and 2 moles of Cl2. This represents a 3:2 (or 1.5:1) ratio of hydrogen to chlorine present for reaction, which is greater than the stoichiometric ratio of 1:1. Hydrogen, therefore, is present in excess, and chlorine is the limiting reactant. The reaction of all the provided chlorine (2 mol) will consume 2 mol of the 3 mol of hydrogen provided, leaving 1 mol of hydrogen unreacted.
An alternative approach to identifying the limiting reactant involves comparing the amount of product expected for the complete reaction of each reactant. Each reactant amount is used to separately calculate the amount of product that would be formed per the reaction’s stoichiometry. The reactant yielding the lesser amount of product is the limiting reactant. For the example in the previous paragraph, the complete reaction of the hydrogen would yield:
![]()
The complete reaction of the provided chlorine would produce:
![]()
The chlorine will be completely consumed once 4 moles of HCl have been produced. Since enough hydrogen was provided to yield 6 moles of HCl, there will be unreacted hydrogen remaining once this reaction is complete. Chlorine, therefore, is the limiting reactant and hydrogen is the excess reactant (Figure 1.3.4).
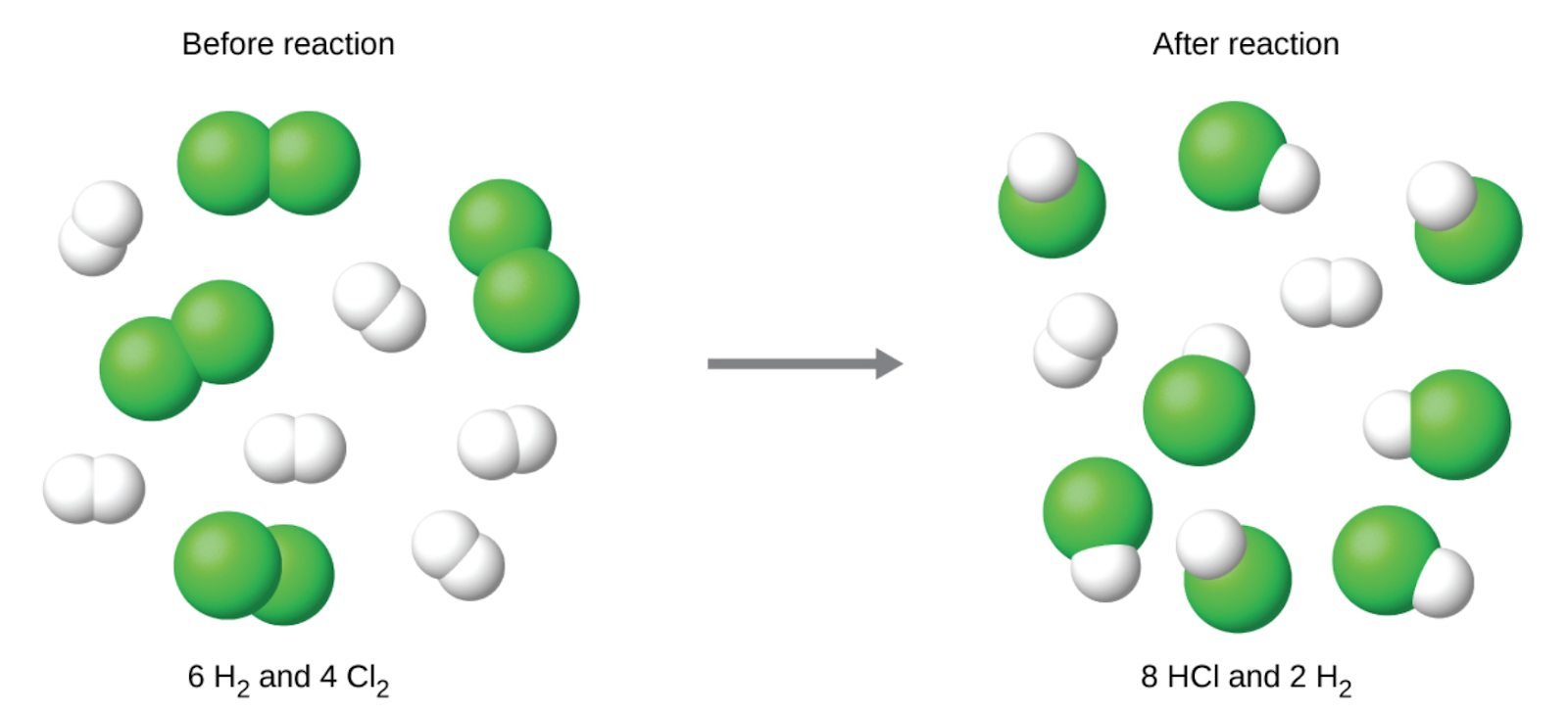 Figure 1.3.4. When H2 and Cl2 are combined in nonstoichiometric amounts, one of these reactants will limit the amount of HCl that can be produced. This illustration shows a reaction in which hydrogen is present in excess and chlorine is the limiting reactant.
Figure 1.3.4. When H2 and Cl2 are combined in nonstoichiometric amounts, one of these reactants will limit the amount of HCl that can be produced. This illustration shows a reaction in which hydrogen is present in excess and chlorine is the limiting reactant.
Example 1.3.5 – Identifying the Limiting Reactant
Silicon nitride is a very hard and high-temperature-resistant ceramic used as a component of turbine blades in jet engines. It is prepared according to the following equation:
3 Si (s) + 2 N2 (g) → Si3N4 (s)
Which is the limiting reactant when 2.00 g of Si and 1.50 g of N2 react?
Solution
Compute the provided molar amounts of reactants, and then compare these amounts to the balanced equation to identify the limiting reactant.
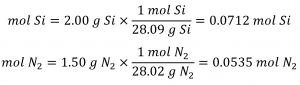
The provided Si: N2 molar ratio is:
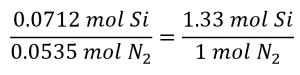
The stoichiometric Si: N2 ratio is:
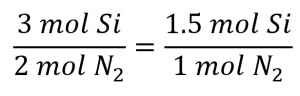
Comparing these ratios shows that Si is provided in a less-than stoichiometric amount, and so is the limiting reactant. Alternatively, compute the amount of product expected for the complete reaction of each of the provided reactants. The 0.0712 moles of silicon would yield: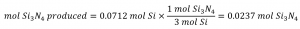
while the 0.0535 moles of nitrogen would produce: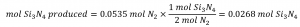
Since silicon yields a lesser amount of product, it is the limiting reactant.
Check Your Learning 1.3.5 – Identifying the Limiting Reactant
Which is the limiting reactant when 5.00 g of H2 and 10.0 g of O2 react and form water? How much excess reagent remains once the reaction has gone to completion?
Answer
Step 1: Write the balanced chemical equation
2 H2 + O2 → 2 H2O
Step 2: Convert the given masses into moles
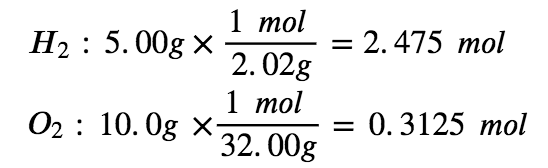
Step 3: Determine the limiting reagent by multiplying the mols of each reactant by the molar ratio.
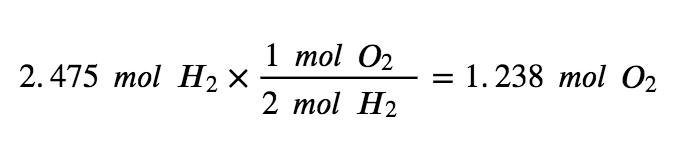
To use up the 2.475 mol of H2 present in this reaction, there would need to be 1.238 mols of oxygen. However, there are only 0.3125 mol of O2 available, making it the limiting reagent
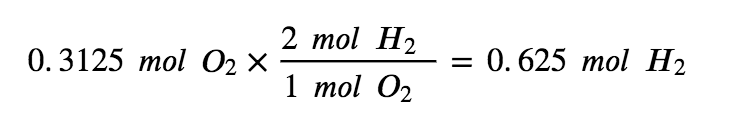
To use up all 0.3125 mols of O2 present in this reaction, we would only need to react 0.625mol of H2 making it the excess reagent (since there are 2.475 mols of H2 present).
Therefore, O2 is the limiting reagent
Step 4: Use the amount of the limiting reactant to find how much H2 was used in the reaction. 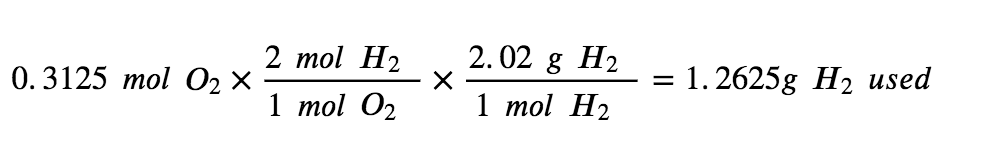
Step 5: To calculate the excess H2 left, subtract the amount used from the total.
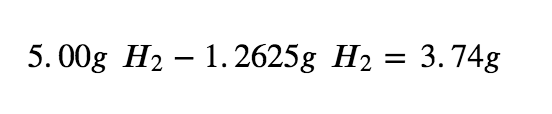
Therefore, 3.74g of H2 is in excess when the reaction has gone to completion
Percent Yield
The amount of product that may be produced by a reaction under specified conditions, as calculated per the stoichiometry of an appropriately balanced chemical equation, is called the theoretical yield of the reaction. In practice, the amount of product obtained is called the actual yield, and it is often less than the theoretical yield for a number of reasons. Some reactions are inherently inefficient, being accompanied by side reactions that generate other products. Others are, by nature, incomplete. Some products are difficult to collect without some loss, so less than perfect recovery will reduce the actual yield. The extent to which a reaction’s theoretical yield is achieved is commonly expressed as its percent yield:![]()
Actual and theoretical yields may be expressed as masses or molar amounts (or any other appropriate property; e.g., volume, if the product is a gas). As long as both yields are expressed using the same units, these units will cancel when the percent yield is calculated.
Example 1.3.6 – Calculation of Percent Yield
Upon reaction of 1.274 g of copper sulfate with excess zinc metal, 0.392 g copper metal was obtained according to the equation:
CuSO4 (aq) + Zn (s) → Cu (s) + ZnSO4 (aq)
What is the percent yield?
Solution
The provided information identifies copper sulfate as the limiting reactant, and so the theoretical yield is found by the approach illustrated in the previous section, as shown here:
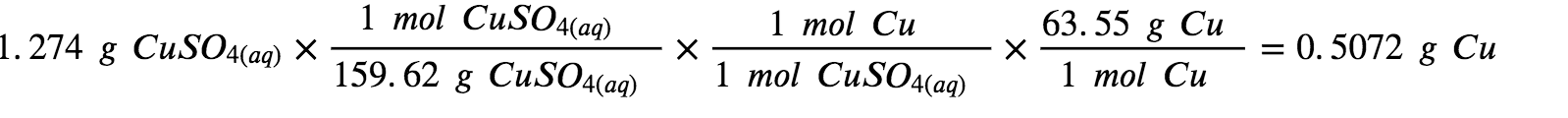
Using this theoretical yield and the provided value for actual yield, the percent yield is calculated to be:
![]()
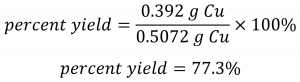
Check Your Learning 1.3.6 – Calculation of Percent Yield
You use the following reaction to produce Freon (CF2Cl2) from CCl4 and HF:
CCl4 + 2 HF → CF2Cl2 + 2 HCl
This reaction has a yield of 75 %. Knowing this, how much HF (in kg) is needed to produce 10 kg of Freon?
Answer
m = 4.40 kg
★ Questions
1. Write the balanced equation, then outline the steps necessary to determine the information requested in each of the following:
(a) The number of moles (in mol) and the mass of chlorine (in grams), Cl2, required to react with 10.0 g of sodium metal, Na, to produce sodium chloride, NaCl.
(b) The number of moles (in mol) and the mass (in grams) of oxygen formed by the decomposition of 1.252 g of mercury (II) oxide.
(c) The number of moles (in mol) and the mass (in grams) of sodium nitrate, NaNO3, required to produce 128 g of oxygen. (NaNO2 is the other product.)
(d) The number of moles (in mol) and the mass (in grams) of carbon dioxide formed by the combustion of 20.0 kg of carbon in an excess of oxygen.
(e) The number of moles (in mol) and the mass (in grams) of copper(II) carbonate needed to produce 1.500 kg of copper(II) oxide. (CO2 is the other product.)
(f) The number of moles and the mass of C2H4Br2 formed by the reaction of 12.85 g of ethene with an excess of Br2.
2. I2 is produced by the reaction of 0.4235 mol of CuCl2 according to the following equation:
2 CuCl2 + 4 KI → 2 CuI + 4 KCl + I2
(a) How many molecules of I2 are produced?
(b) What mass of I2 is produced (in grams)?
3. Silver is often extracted from ores such as K[Ag(CN)2] and then recovered by the reaction:
2 K[Ag(CN)2] (aq) + Zn (s) → 2 Ag (s) + Zn(CN)2 (aq) + 2 KCN (aq)
(a) How many molecules of Zn(CN)2 are produced by the reaction of 35.27 g of K[Ag(CN)2]?
(b) What mass of Zn(CN)2 is produced (in grams)?
4. Carborundum is silicon carbide, SiC, a very hard material used as an abrasive on sandpaper and in other applications. It is prepared by the reaction of pure sand, SiO2, with carbon at high temperature. Carbon monoxide, CO, is the other product of this reaction. Write the balanced equation for the reaction, and calculate how much (mass, in grams) SiO2 is required to produce 3.00 kg of SiC.
★★ Questions
5. In an accident, a solution containing 2.5 kg of nitric acid was spilled. Two kilograms of Na2CO3 was quickly spread on the area and CO2 was released by the reaction. Was sufficient Na2CO3 used to neutralize all of the acid?
6. A sample of 0.53 g of carbon dioxide was obtained by heating 1.31 g of calcium carbonate. What is the percent yield for this reaction?
CaCO3 (s) → CaO (s) + CO2 (s)
7. Freon-12, CCl2F2, is prepared from CCl4 by reaction with HF. The other product of this reaction is HCl. Outline the steps needed to determine the percent yield of a reaction that produces 12.5 g of CCl2F2 from 32.9 g of CCl4. Freon-12 has been banned and is no longer used as a refrigerant because it catalyzes the decomposition of ozone and has a very long lifetime in the atmosphere. Determine the percent yield.
8. Citric acid, C6H8O7, a component of jams, jellies, and fruity soft drinks, is prepared industrially via fermentation of sucrose by the mold Aspergillus niger. What mass of citric acid (in grams) is produced from exactly 1 metric ton (1.000 × 103 kg) of sucrose if the yield is 92.30 %? The equation representing this reaction is:
C12H22O11 + H2O + 3 O2 → 2 C6H8O7 + 4 H2O
9. Outline the steps needed to determine the limiting reactant when 30.0 g of propane, C3H8, is burned with 75.0 g of oxygen. Determine the limiting reactant.
10. What is the limiting reactant when 1.50 g of lithium and 1.50 g of nitrogen combine to form lithium nitride, a component of advanced batteries, according to the following unbalanced equation:
Li + N2 → Li3N (unbalanced)
11. Uranium can be isolated from its ores by dissolving it as UO2(NO3)2, then separating it as solid UO2(C2O4)·3H2O. Addition of 0.4031 g of sodium oxalate, Na2C2O4, to a solution containing 1.481 g of uranyl nitrate, UO2(NO3)2, yields 1.073 g of solid UO2(C2O4)·3H2O.
Na2C2O4 + UO2(NO3)2 + 3 H2O → UO2(C2O4)∙3H2O + 2 NaNO3
Determine the limiting reactant and the percent yield of this reaction.
12. The phosphorus pentoxide used to produce phosphoric acid for cola soft drinks is prepared by burning phosphorus in oxygen.
(a) What is the limiting reactant when 0.200 mol of P4 and 0.200 mol of O2 react according to:
P4 + 5 O2 ⟶ P4O10
(b) Calculate the percent yield if 10.0 g of P4O10 is isolated from the reaction.
Answers
1. (a) Cl2 (g) + 2 Na (s) → 2 NaCl (aq), 0.435 mol Na, 0.217 mol Cl2, 15.4 g Cl2
(b) 2 HgO (s) → 2 Hg (s) + O2 (g), 0.005780 mol HgO, 2.890 × 10−3 mol O2, 9.248 × 10−2 g O2
(c) 2 NaNO3 (s) → O2 (g) + 2 NaNO2 (s), 8.00 mol NaNO3, 6.8 × 102 g NaNO3
(d) C (s) + O2 (g) → CO2 (g), 1665 mol CO2, 73.3 kg CO2
(e) CuCO3 (s) → CuO (s) + CO2 (g), 18.86 mol CuO, 2.330 kg CuCO3
(f) C2H4Br2 → C2H4 + Br2, 0.4580 mol C2H4Br2, 86.05 g C2H4Br2
2. (a) 1.28 × 1023 molecules; (b) 26.9 g
3. (a) 5.337 × 1022 molecules; (b) 10.41 g Zn(CN)2
4. 4.50 kg, SiO2, SiO2 + 3 C → SiC + 2 CO
5. Yes – recognize that there is a 2:1 mole ratio of HNO3 : Na2CO3 in the balanced chemical equation for this neutralization reaction. Hence, we need at least 2 moles of Na2CO3 for every 1 mole of HNO3 to neutralize all of the acid. The given quantities (in kg) correspond to molar quantities of 39.67 mol HNO3 : 18.87 mol Na2CO3; this is a 2:1 mole ratio (2X more sodium carbonate than acid). Therefore, sufficient Na2CO3 was used to neutralize all of the acid.
6. 92.0 %
7. Percent yield = 48.3 %, g CCl4 ⟶ mol CCl4 ⟶ mol CCl2F2 ⟶ g CCl2F2
8. 1.03 tonnes
9. (1) Determine the balanced chemical equation: C3H6 + 5 O2 → 3 CO2 + 4 H2O; (2) Using the given masses and the reactants’ molar mass, find the moles for both propane and oxygen; (3) With the moles found in the previous step, find the mole of carbon dioxide with the mole ratios based on the balanced chemical equation; (4) With these two values, determine the mass of carbon dioxide. The reactant which results in the smallest mass of carbon dioxide is the limiting reactant. In this case it is oxygen.
10. Li is the limiting reactant
11. Na2C2O4 is the limiting reactant. percent yield = 86.6 %
12. (a) O2 is the limiting reactant; (b) 88 %
Relationships between the amounts of reactants and products of a chemical reaction
The ratio of coefficients in a balanced chemical equation, used in computations relating amounts of reactants and products
Reactant present in an amount lower than required by the reaction stoichiometry; it runs out first for a given chemical reaction and thus limits the amount of product generated
Reactant present in an amount greater than required by the reaction stoichiometry
Amount of product that may be produced from a given amount of reactant(s) according to the reaction stoichiometry
The actual amount of product formed in a chemical reaction
A measure of the efficiency of a reaction expressed as a percentage of the theoretical yield; actual yield divided by theoretical yield times 100% to give a percentage between 0% and 100%

