7.1 – Introduction to Reaction Rates
In previous units, we’ve covered several different variables to describe a chemical reaction – in thermochemistry, we saw that we can use ΔH to tell if a reaction is energetically favourable, and in our discussion of chemical equilibria, we saw that we can use K, the equilibrium constant, to tell if a reaction favours products or reactants. However, we haven’t yet discussed how we can describe how fast a reaction proceeds. This will be covered here when we talk about kinetics – the study of reaction rates and the mechanisms that explain how fast or slow a reaction proceeds.
A rate is a measure of how some property varies with time. Speed is a familiar rate that expresses the distance travelled by an object in a given amount of time. Wage is a rate that represents the amount of money earned by a person working for a given amount of time. Likewise, the rate of a chemical reaction is a measure of how much reactant is consumed, or how much product is produced, by the reaction in a given amount of time.
The rate of reaction is the change in the amount of a reactant or product per unit time. Reaction rates are therefore determined by measuring the time dependence of some property that can be related to reactant or product amounts. Rates of reactions that consume or produce gaseous substances, for example, are conveniently determined by measuring changes in volume or pressure. For reactions involving one or more coloured substances, rates may be monitored via measurements of light absorption. For reactions involving aqueous electrolytes, rates may be measured via changes in a solution’s conductivity.
For reactants and products in solution (the most common case), reaction rates are usually expressed as the concentration of reactant consumed or the concentration of product formed per unit time. The units are thus moles per litre per unit time, written as M/s, M/min, or M/h. To measure reaction rates, chemists initiate the reaction, measure the concentration of the reactant or product at different times as the reaction progresses, perhaps plot the concentration as a function of time on a graph, and then calculate the change in concentration per unit time.
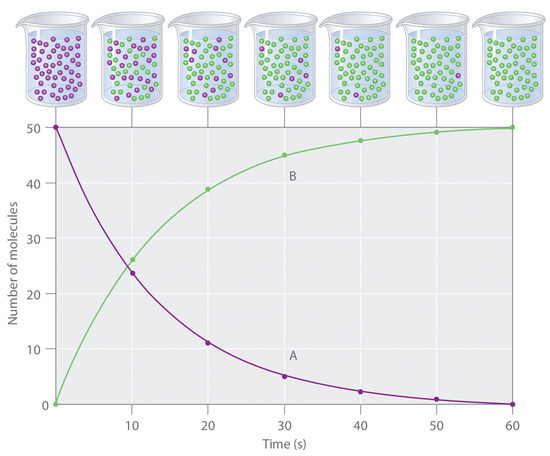
Figure 7.1.1. The progress of a simple reaction (A → B). The mixture initially contains only A molecules (purple). Over time, the number of A molecules decreases and more B molecules (green) are formed (top). The graph shows the change in the number of A and B molecules in the reaction as a function of time over a 1 min period (bottom).
The progress of a simple reaction (A → B) is shown in Figure 7.1.1; the beakers are snapshots of the composition of the solution at 10 s intervals. The number of molecules of reactant (A) and product (B) are plotted as a function of time in the graph. Each point in the graph corresponds to one beaker in Figure 7.1.1. The reaction rate is the change in the concentration of either the reactant or the product over a period of time. The concentration of A decreases with time, while the concentration of B increases with time.
Equation 7.1.1 Rate Relation to Concentration of Reactants
Square brackets indicate molar concentrations, and the capital Greek delta (Δ) means “change in.” Due to it being a common practice among chemists to follow the convention of expressing all reaction rates as positive numbers, a negative sign is inserted in front of Δ[A]/Δt to convert the otherwise negative rate into a positive number. The reaction rate calculated for the reaction A → B using the equation above is different for each interval (this is not true for every reaction, as shown below). For example, a greater change occurs in [A] and [B] during the first 10 s interval than during the last, meaning that the reaction rate is greatest at first. Hence, an important thing to keep in mind is that reaction rates generally decrease with time as reactant concentrations decrease.
Let’s apply what we’ve just learned with an example of a reaction – if we measure the concentration of hydrogen peroxide, H2O2, in an aqueous solution, we find that it changes slowly over time as the H2O2 decomposes, according to the equation:
The rate at which the hydrogen peroxide is consumed can be expressed in terms of the rate of change of its concentration, as shown here:
Equation 7.1.2 Rate of Decomposition
[H2O2]1 represents the molar concentration of hydrogen peroxide at some time t1; likewise, [H2O2]2 represents the molar concentration of hydrogen peroxide at a later time t2; and Δ[H2O2] represents the change in molar concentration of hydrogen peroxide during the time interval Δt (that is, t2 − t1). When dealing with rates of reaction, it is important to consider stoichiometric coefficients. For the decomposition of hydrogen peroxide, as H2O and H2O2 have the same coefficients we can conclude the magnitude of their rate of formation and decomposition are identical. As for the O2, using stoichiometric ratios we can conclude that the magnitude of its rate of formation is half of the other 2 molecules.
NOTE: Remember that (as previously mentioned) reaction rates are, by convention, positive. Since the reactant concentration decreases as the reaction proceeds, Δ[H2O2] is a negative quantity; we place a negative sign in front of the expression to express the reaction rate as a positive quantity.
Factors Affecting Reaction Rates
The rates at which reactants are consumed and products are formed during chemical reactions vary greatly. We can identify five factors that affect the rates of chemical reactions: the chemical nature of the reacting substances, the state of subdivision (one large lump versus many small particles) of the reactants, the temperature of the reactants, the concentration of the reactants, and the presence of a catalyst.
The Chemical Nature of the Reacting Substances
The rate of a reaction depends on the nature of the participating substances. Reactions that appear similar may have different rates under the same conditions, depending on the identity of the reactants. For example, when small pieces of the metals iron and sodium are exposed to air, the sodium reacts completely with air overnight, whereas the iron is barely affected. The active metals calcium and sodium both react with water to form hydrogen gas and a base. Yet calcium reacts at a moderate rate, whereas sodium reacts so rapidly that the reaction is almost explosive.
The State of Subdivision of the Reactants
Except for substances in the gaseous state or in solution, reactions occur at the boundary, or interface, between two phases. Hence, the rate of a reaction between two phases depends to a great extent on the surface contact between them. A finely divided solid has more surface area available for reaction than does one large piece of the same substance. Thus a liquid will react more rapidly with a finely divided solid than with a large piece of the same solid. For example, large pieces of iron react slowly with acids; finely divided iron reacts much more rapidly (Figure 7.1.2). Large pieces of wood smoulder, smaller pieces burn rapidly, and sawdust burns explosively.

(a) (b)
Figure 7.1.2. (a) Iron powder reacts rapidly with dilute hydrochloric acid and produces bubbles of hydrogen gas because the powder has a large total surface area:
2Fe(s) + 6HCl(aq) ⟶ 2FeCl3(aq) + 3H2(g). (b) An iron nail reacts more slowly.
|
Reaction of Cesium with Water – Video Demonstration |
|
Watch this video to see the reaction of cesium with water in slow motion and a discussion of how the state of reactants and particle size affect reaction rates. |
Temperature of the Reactants
Chemical reactions typically occur faster at higher temperatures. Food can spoil quickly when left on the kitchen counter. However, the lower temperature inside of a refrigerator slows that process so that the same food remains fresh for days. We use a burner or a hot plate in the laboratory to increase the speed of reactions that proceed slowly at ordinary temperatures. In many cases, an increase in temperature of only 10°C will approximately double the rate of a reaction in a homogeneous system.
Concentrations of the Reactants
The rates of many reactions depend on the concentrations of the reactants. Rates usually increase when the concentration of one or more of the reactants increases. For example, calcium carbonate (CaCO3) deteriorates as a result of its reaction with the pollutant sulfur dioxide. The rate of this reaction depends on the amount of sulfur dioxide in the air (Figure 7.1.3). An acidic oxide, sulfur dioxide combines with water vapour in the air to produce sulfurous acid in the following reaction:
Calcium carbonate reacts with sulfurous acid as follows:
In a polluted atmosphere where the concentration of sulfur dioxide is high, calcium carbonate deteriorates more rapidly than in less polluted air. Similarly, phosphorus burns much more rapidly in an atmosphere of pure oxygen than in air, which is only about 20% oxygen.

Figure 7.1.3. Statues made from carbonate compounds such as limestone and marble typically weather slowly over time due to the actions of water, and thermal expansion and contraction. However, pollutants like sulfur dioxide can accelerate weathering. As the concentration of air pollutants increases, the deterioration of limestone occurs more rapidly. (credit: James P Fisher III)
|
Phosphorus Burning in Air with Higher [O2] – Video Demonstration |
|
Phosphorus burns rapidly in air, but it will burn even more rapidly if the concentration of oxygen is higher. Watch this video to see an example. |
The Presence of a Catalyst
Hydrogen peroxide solutions foam when poured onto an open wound because substances in the exposed tissues act as catalysts, increasing the rate of hydrogen peroxide’s decomposition. However, in the absence of these catalysts (for example, in the bottle in the medicine cabinet) complete decomposition can take months. A catalyst is a substance that increases the rate of a chemical reaction by lowering the activation energy without itself being consumed by the reaction. Activation energy is the minimum amount of energy required for a chemical reaction to proceed in the forward direction. A catalyst increases the reaction rate by providing an alternative pathway or mechanism for the reaction to follow. Catalysis will be discussed in greater detail later in this chapter as it relates to mechanisms of reactions.
|
Factors Affecting Reaction Rates – Interactive Activity |
|
Chemical reactions occur when molecules collide with each other and undergo a chemical transformation. Before physically performing a reaction in a laboratory, scientists can use molecular modelling simulations to predict how the parameters discussed earlier will influence the rate of a reaction. Use the PhET Reactions & Rates interactive to explore how temperature, concentration, and the nature of the reactants affect reaction rates. |
Questions
★ Questions
Describe the effect of each of the following on the rate of the reaction of magnesium metal with a solution of hydrochloric acid: the molarity of the hydrochloric acid, the temperature of the solution, and the size of the pieces of magnesium.
Explain why an egg cooks more slowly in boiling water in Lake Louise, AB(elevation 1.6km) than in Charlottetown, PEI(elevation 0-49m). (Hint: Consider the effect of temperature on reaction rate and the effect of pressure on boiling point.)
What is the difference between average rate, initial rate, and instantaneous rate?
In the nuclear industry, chlorine trifluoride is used to prepare uranium hexafluoride, a volatile compound of uranium used in the separation of uranium isotopes. Chlorine trifluoride is prepared by the reaction Cl2 (g) + 3F2 (g) ⟶ 2ClF3 (g). Write the equation that relates the rate expressions for this reaction in terms of the disappearance of Cl2 and F2 and the formation of ClF3.
Answers
Higher molarity increases the rate of the reaction. Higher temperature increases the rate of the reaction. Smaller pieces of magnesium metal will react more rapidly than larger pieces because a more reactive surface exists.
The boiling points in this question are dependent on the elevation of our two cities. The higher the elevation, the lower the air pressure; when we reduce the pressure over boiling water, it is able to boil at a lower temperature. This affects the rate at which our egg will cook because the lower temperature will decrease the rate of our reaction.
The instantaneous rate is the rate of a reaction at any particular point in time, a period of time that is so short that the concentrations of reactants and products change by a negligible amount. The initial rate is the instantaneous rate of reaction as it starts (as the product just begins to form). The average rate is the average of the instantaneous rates over a time period.
Measure of the speed at which a chemical reaction takes place
Substance that lowers the activation energy of a specific reaction by providing an alternate reaction pathway, thereby increasing the rate of a reaction without itself being consumed by the reaction

