6.1 – Common-Ion Effect

The common ion effect is used to describe the effect on an existing equilibrium by the addition of a second substance that contains an ion common to the equilibrium. If several salts are present in a system, they all ionize in the solution. If the salts contain a common cation or anion, these salts contribute to the concentration of the common ion. Contributions from all salts must be included in the calculation of concentration of the common ion.

Common Ions

When NaCl and KCl, both very soluble salts, are dissolved in the same solution, the Cl⁻ ions are common to both salts. In a system containing NaCl and KCl, the Cl^– ions are common ions.

NaCl (s) → Na⁺ (aq) + Cl^– (aq)

KCl (s) → K⁺ (aq) + Cl^– (aq)

Since both salts ionize completely in solution, we can use stoichiometry to express the concentrations of the dissolved ions in solution in the following equation:

[Na⁺] + [K⁺] = [Cl^–]

You may recognize the above equivalence as an application of the concepts of charge balance and mass balance.

Example 6.1.1 – Concentrations of Common Ions

What are [Na⁺], [Cl^–], [Ca²⁺], and [H₃O⁺] in a solution containing 0.10 M each of NaCl, CaCl₂, and HCl?

Solution

All three species ionize completely in water:

NaCl (s) → Na⁺ (aq) + Cl^– (aq)

HCl (aq) + H₂O (l) → H₃O⁺ (aq) + Cl^– (aq)

CaCl₂ (s) → Ca²⁺ (aq) + 2Cl^– (aq)

Using stoichiometry, we see that each mol of dissolved compound produces a mol of cations. Therefore, due to the conservation of ions, we have:

[Na⁺] = [Ca²⁺] = [H₃O⁺] = 0.10 M

Each compound produces chloride ions; however, we note that calcium chloride produces 2 mol of Cl^– ions for every mol of CaCl₂ dissolved. Therefore, the total amount of chloride ion in solution is:

[Cl^–] = 0.10 M(due to NaCl) + 0.20 M(due to CaCl₂) + 0.10 M(due to HCl)

[Cl^–] = 0.40 M

Example 6.1.2 – Common Ion Calculations

You pour 10.0 mL of 0.10 M NaCl, 10.0 mL of 0.10 M KOH and 5.0 mL of 0.20 M HCl aqueous solutions together in a 100.0 mL volumetric flask, and then fill the flask to the calibration mark with distilled water. What is [Cl-] in the final solution? 

Solution

Notice that the chloride ions are common to two of the three solutes, NaCl and HCl. First, find the number of moles of added chloride ions (note that the volumes have already been converted into litres): 

Now, determine the concentration, using the total volume of solution: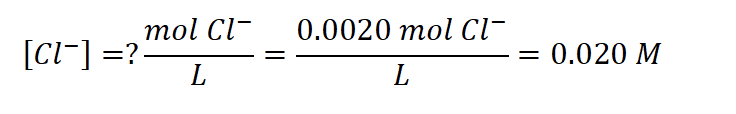   

Common Ion Effect and Equilibria

In the above examples, since all of the compounds undergo 100% ionization, we could use simple stoichiometry to find the concentrations of the common ion. But what happens if we involve substances that only partially ionize in solution? What effect would a common ion have on an equilibrium?

Le Châtelier’s Principle states that if an equilibrium becomes unbalanced, the reaction will shift in order to restore the balance. Consider the following chemical equation, representing the ionization of a generic weak acid:

HA + H₂O ⇌ H₃O⁺ + A^–

If we were to add a second substance, for example, the sodium salt of the conjugate base (NaA) to this solution, then this soluble salt would increase the concentration of the A^– ion in solution:

NaA (s) → Na⁺ (aq) + A^– (aq)

The A^– ion is the common ion to both chemical equations, but note their differences: the first is an equilibrium but the second goes to completion. Thus, the presence of the sodium salt increases the concentration of conjugate base. According to Le Chatelier’s Principle, increased [A^–] means that the weak acid equilibrium will shift towards the reactants.

In general, we can conclude that adding a common ion prevents a weak acid (or similarly, a weak base) from ionizing as much as it would without the added common ion. The common ion effect suppresses the ionization of a weak acid by adding more of an ion that is a product of this equilibrium. Adding a common ion to a system at equilibrium affects the equilibrium composition, but not the ionization constant. The example below, involving the dissolution of a slightly soluble salt, illustrates this important concept.

Example 6.1.3 – Common Ion Added to a System at Equilibrium

Calcium hydroxide is a sparingly soluble salt that exists in equilibrium in aqueous solution with its ions. A solution of Ca(OH)₂ at equilibrium contains [Ca²⁺] = 0.0108 M, [OH^–] = 0.0216 M, and some solid salt. To this solution, you add some solid calcium chloride, which ionizes completely into Ca²⁺ and Cl^– and allow the system to re-establish equilibrium. When you re-measure the ion concentrations, you find the solution now contains [Ca²⁺] = 0.0374 M and [OH^–] = 0.0116 M. Calculate the equilibrium constant for the dissolution of calcium hydroxide before and after the addition of calcium chloride, rounding to 2 significant figures. What can you conclude when you compare these values?

Solution

First, write out the chemical equation for the dissolution of calcium hydroxide at equilibrium:

Ca(OH)₂ (s) ⇌ Ca²⁺ (aq) + 2OH^– (aq)

The equilibrium constant expression for the above equilibrium is:

K = [Ca²⁺][OH^–]²

Substituting the concentrations of calcium and hydroxide ions present at equilibrium before the addition of calcium chloride, we obtain:

K = (0.0108)(0.0216)²

K = 5.0×10^–6

Now, we recalculate K using the concentrations after the addition of the salt containing the common ion:

K = (0.0374)(0.0116)²

K = 5.0×10^–6

Comparing these values, we can conclude that, while the equilibrium concentrations of ions change, the value of the equilibrium constant itself does not change with the addition of a common ion.

Returning to our discussion of weak acids, we now know that the presence of a common ion suppresses the ionization of the weak acid, decreasing the concentrations of the product ions, but does not affect the equilibrium constant, K_a. This is illustrated below in Figure 6.1.1: adding a strong acid, such as HCl, to a solution of a weak acid shifts the equilibrium towards the reactants. HCl ionizes completely, increasing the concentration of H₃O⁺, which then suppresses the ionization of the weak acid present, acetic acid.

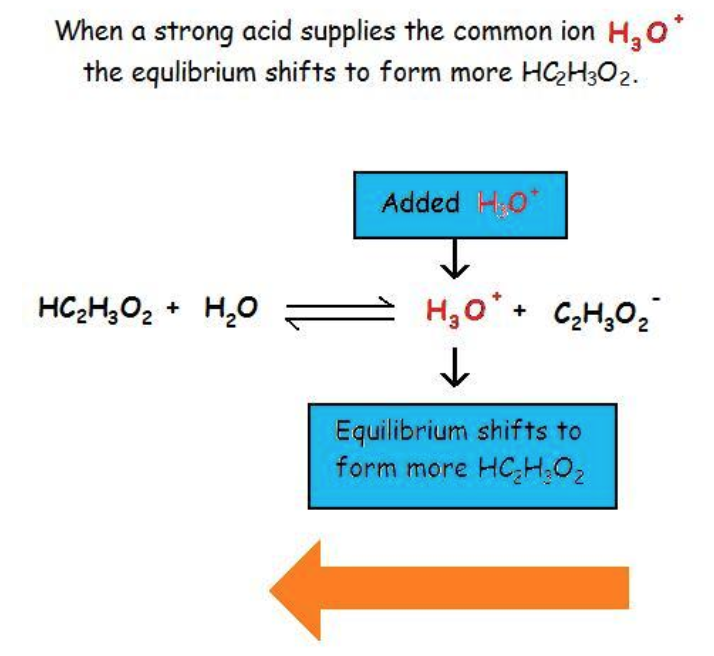
Figure 6.1.1. Adding a strong acid (e.g. HCl) to a solution of acetic acid (a weak acid) shifts the equilibrium towards reactants, thus inhibiting the ionization of the weak acid.

The common ion effect also suppresses the ionization of a weak base by again increasing the concentration of a product ion of the equilibrium. For example, Figure 6.1.2 shows the common ion effect of the addition of OH^– (from a strong base) on the ionization of ammonia, a weak base.

Figure 6.1.2. Adding a strong base (e.g. NaOH) to a solution of ammonia (a weak base) shifts the equilibrium towards reactants, thus inhibiting the ionization of the weak base.

Adding a strong base such as NaOH, causes the concentration of the common ion of hydroxide to increase, and thus increases the reaction quotient, Q:

Q > K, and thus the system is no longer at equilibrium. To re-establish equilibrium, the value of Q must be decreased by decreasing the amount of products and increasing the amount of reactant. Therefore, the reaction shifts to the left to counteract the imbalance (in accordance with Le Châtelier’s Principle), forming more reactants. This decreases Q until it equals the equilibrium constant, K_b = 1.8 x 10^-5, and a new equilibrium point is reached.

Example 6.1.4 – Common Ion Added to a System at Equilibrium

What is the pH of a 0.100 M solution of HOCl? What is the pH of a solution that contains both 0.100 M HOCl and 0.010 HCl? What can you conclude by comparing these two values?

Solution

HOCl is a weak acid, with K_a = 4.0×10^–8. We use an ICE table to find the hydronium ion concentration at equilibrium and then the pH:

HOCl + H₂O ⇌ H₃O⁺ + OCl^–

K_a = 4.0×10^-8 = ([H₃O⁺][OCl^–])/[HOCl]

4.0×10^-8 = x²/(0.100-x)

x = 6.3×10^–5 M = [H₃O⁺]

pH = 4.20

Now, we repeat this calculation, but this time taking into account the 0.010 M H₃O⁺ formed from the complete ionization of the strong acid, HCl:

HOCl + H₂O ⇌ H₃O⁺ + OCl^–

K_a = 4.0×10^-8 = ([H₃O⁺][OCl^–])/[HOCl]

4.0×10^-8 = ((0.010+x)(x))/(0.100-x)

x = 4.0×10^–7 M

[H₃O⁺] = 0.010 + x = 0.010 M + 4.0×10^–7 M = 0.010 M

pH = 2.00

In both cases, we made the assumption that “x is small” to simplify the calculation (verifying the result confirms that this assumption is valid). Comparing the two results, we see that in the second case, nearly 100% of the hydronium ion at equilibrium comes from the strong acid source, HCl. In the presence of the strong acid, very little of the HOCl ionizes, illustrating the common ion effect on this equilibrium.

Check Your Learning 6.1.4 – Common Ion Added to a System at Equilibrium

What is the pH of a solution of 0.150 M NH₃ and 0.045 M NH₄Cl?

Answer

pH = 9.78

★ Questions

1. To a 250.0 mL volumetric flask, a lab technician adds the following: 5.65 g of potassium nitrite, 3.08 g of magnesium nitrite, and 35.0 mL of a 0.270 M solution of nitrous acid. She then fills the flask with distilled water to the calibration mark. Determine the concentrations of all the ions present in the final solution. (You may assume that both salts dissolve completely in solution). 

2. Calculate the pH of: 

Answers

1. [K⁺] = 0.266 M, [Mg²⁺] = 0.106 M, [H₃O⁺] = 4.43×10^–5 M, [NO₂^–] = 0.477 M, [OH^–] = 2.26x10^–10 M. (Not an ion, but [HNO₂] = 0.0378 M) 

2. a)10.72,  b) 12.18,  c) 8.95 

3.a) More Cl^– ions means to counteract the change by making more solid PbCl₂, therefore the equilibrium will shift to the left.

b) PbCl₂ and KCl both share a common ion, Cl^– Due to this there is a shift in equilibrium properties.

c) At equilibrium, Qsp=Ksp. Adding more chloride ion makes Qsp>Ksp. To decrease the value of Q, the system moves to the left.

4. a) Ksp= [Ca²⁺][IO₃^-2]

Ksp= 4 x (5.6×10^-3)³= 7.03 x 10^-7

b) The precipitate formed is Ca(IO₃)_2. This is due to the common ion effect.

5. [H⁺]= 10^-13.25= 5.62 x 10^-14

[OH^–]= Kw/ [H⁺] = (1.0 x 10^-14)/ (5.62 x 10^-14) = 0.18mol/L

6. Step 1: Calculate [OH^–]

Kb= ([NH₄⁺] [OH]) / [NH₃]

1.77 x 10^-5= [(0.2073) (x)]/ 0.7174

x = 6.10 x 10^-5 M

Step 2: Use the K_sp expression to calculate the [Mg²⁺]

Ksp= [Mg²⁺] [OH^–]²

1.2 x 10^-11= (s) (6.10 x 10^-5)²

s = 3.2 x 10^-3 M