1.4 – Solution Stoichiometry

Molarity

In preceding sections, we focused on the composition of substances: samples of matter that contain only one type of element or compound. However, mixtures—samples of matter containing two or more substances physically combined—are more commonly encountered in nature than are pure substances. Similar to a pure substance, the relative composition of a mixture plays an important role in determining its properties. The relative amount of oxygen in a planet’s atmosphere determines its ability to sustain aerobic life. The relative amounts of iron, carbon, nickel, and other elements in steel (a solid mixture known as an “alloy”) determine its physical strength and resistance to corrosion. The relative amount of the active ingredient in a medicine determines its effectiveness in achieving the desired pharmacological effect. The relative amount of sugar in a beverage determines its sweetness (see Figure 1.4.1.). In this section, we will describe one of the most common ways in which the relative compositions of mixtures may be quantified.

Figure 1.4.1. Sugar is one of many components in the complex mixture known as coffee. The amount of sugar in a given amount of coffee is an important determinant of the beverage’s sweetness. (credit: Jane Whitney)

Solutions

We have previously defined solutions as homogeneous mixtures, meaning that the composition of the mixture (and therefore its properties) is uniform throughout its entire volume. Solutions occur frequently in nature and have also been implemented in many forms of manmade technology. We will explore a more thorough treatment of solution properties in the chapter on solutions and colloids, but here we will introduce some of the basic properties of solutions.

The relative amount of a given solution component is known as its concentration. Often, though not always, a solution contains one component in an amount that is significantly greater than that of all other components. This component is called the solvent and may be viewed as the medium in which the other components are dispersed, or dissolved. Solutions in which water is the solvent are, of course, very common on our planet. A solution in which water is the solvent is called an aqueous solution.

A solute is the component of a solution that is present in a much lower amount than the solvent. Solute concentrations are often described with qualitative terms such as dilute (of relatively low concentration) and concentrated (of relatively high concentration).

Concentrations may be quantitatively assessed using a wide variety of measurement units, each convenient for particular applications. Molarity (M) is a useful concentration unit for many applications in chemistry. Molarity is defined as the number of moles of solute in exactly 1 litre (1 L) of the solution: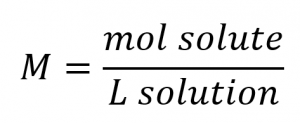

Example 1.4.1 – Calculating Molar Concentrations

A 355 mL soft drink sample contains 0.133 mol of sucrose (table sugar). What is the molar concentration of sucrose in the beverage?

Solution

Since the molar amount of solute and the volume of the solution are both given, the molarity can be calculated using the definition of molarity. Per this definition, the solution volume must be converted from mL to L:

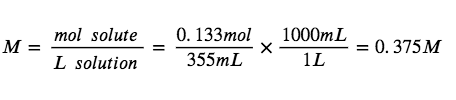
Check Your Learning 1.4.1 – Calculating Molar Concentrations

A teaspoon of table sugar contains about 0.01 mol sucrose. What is the molarity of sucrose if a teaspoon of sugar has been dissolved in a cup of tea with a volume of 200 mL?

Answer

M = 0.05 mol/L

Example 1.4.2 – Deriving Moles and Volumes from Molar Concentrations

How much sugar (mol) is contained in a modest sip (~10 mL) of the soft drink from the previous example?

Solution

In this case, we can rearrange the definition of molarity to isolate the quantity sought, moles of sugar. We then substitute the value for molarity that we derived in the previous example, 0.375 mol/L:

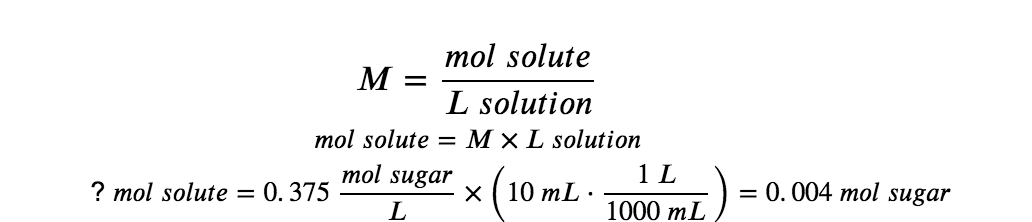
Check Your Learning 1.4.2 – Deriving Moles and Volumes from Molar

Concentrations

What volume (mL) of the sweetened tea described in the previous example contains the same amount of sugar (mol) as 10 mL of the soft drink in this example?

Answer

V = 80 mL

Example 1.4.3 – Calculating Molar Concentrations from the Mass of Solute

Distilled white vinegar (Figure 1.4.2) is a solution of acetic acid, CH₃CO₂H, in water. A 0.500 L vinegar solution contains 25.2 g of acetic acid. What is the concentration of the acetic acid solution in units of molarity?

Figure 1.4.2. Distilled white vinegar is a solution of acetic acid in water.

Solution

As in previous examples, the definition of molarity is the primary equation used to calculate the quantity sought. In this case, the mass of solute is provided instead of its molar amount, so we must use the solute’s molar mass to obtain the amount of solute in moles:

First, find the number of moles of the solute: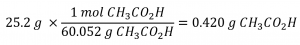

Next, we find the molarity: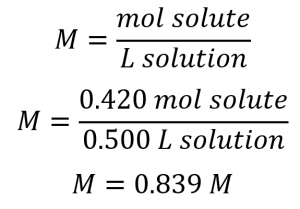

In other words: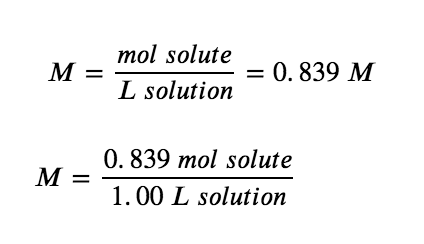        

Check Your Learning 1.4.3 – Calculating Molar Concentrations from the Mass of

Solute

Calculate the molarity of 6.52 g of CoCl₂ (128.9 g/mol) dissolved in an aqueous solution with a total volume of 75.0 mL.

Answer

0.674 mol/L

Example 1.4.4 – Determining the Mass of Solute in a Given Volume of Solution

How many grams of NaCl are contained in 0.250 L of a 5.30 mol/L solution?

Solution

The volume and molarity of the solution are specified, so the amount (mol) of solute is easily computed as demonstrated in the second example: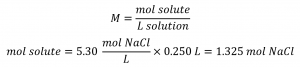

Finally, this molar amount is used to derive the mass of NaCl:

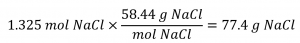
Check Your Learning 1.4.4 – Determining the Mass of Solute in a Given Volume of Solution

How many grams of CaCl₂ (110.98 g/mol) are contained in 250.0 mL of a 0.200 mol/L solution of calcium chloride?

Answer

5.55 g CaCl₂

When performing calculations stepwise, as in the previous example, it is important to refrain from rounding any intermediate calculation results, which can lead to rounding errors in the final result. In the previous example, the molar amount of NaCl computed in the first step, 1.325 mol, would be properly rounded to 1.32 mol if it were to be reported; however, although the last digit (5) is not significant, it must be retained as a guard “extra” digit in the intermediate calculation. If we had not retained this guard digit, the final calculation for the mass of NaCl would have been 77.1 g, a difference of 0.3 g.

In addition to retaining a guard digit for intermediate calculations, we can also avoid rounding errors by performing computations in a single step (see the next example). This eliminates intermediate steps so that only the final result is rounded.

Example 1.4.5 – Determining the Volume of Solution Containing a Given Mass of Solute

In the Example 1.4.3, we found the typical concentration of vinegar to be 0.839 mol/L. What volume of vinegar contains 75.6 g of acetic acid?

Solution

First, use the molar mass to calculate moles of acetic acid from the given

mass:

Then, use the molarity of the solution to calculate the volume of the solution containing this molar amount of solute:

Combining these two steps into one yields:

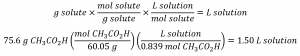
Check Your Learning 1.4.5 – Determining the Volume of Solution Containing a Given Mass of Solute

What volume of a 1.50 mol/L KBr solution contains 66.0 g KBr?

Answer

V = 0.370 L

Other Units for Solution Concentrations

Mass Percentage

Earlier in this chapter, we introduced percent composition as a measure of the relative amount of a given element in a compound. Percentages are also commonly used to express the composition of mixtures, including solutions. The mass percentage of a solution component is defined as the ratio of the component’s mass to the solution’s mass, expressed as a percentage:

We are generally most interested in the mass percentages of solutes, but it is also possible to compute the mass percentage of solvent. When expressing mass percent, you can use any measurement system you choose, but the same units must be used on both the top and the bottom of the equation and the denominator is always 100 (for example: g/100 g, oz/100 oz ie, “x parts of solute per 100 parts of solvent”).

Mass percentage is also referred to by similar names such as percent mass, percent weight, weight/weight percent, and other variations on this theme. The most common symbol for mass percentage is simply the percent sign, %, although more detailed symbols are often used including % mass, % weight, and (w/w)%. Use of these more detailed symbols can prevent confusion of mass percentages with other types of percentages, such as volume percentages (to be discussed later in this section).

Mass percentages are popular concentration units for consumer products. The label of a typical liquid bleach bottle (Figure 1.4.3) cites the concentration of its active ingredient, sodium hypochlorite (NaOCl), as being 7.4 %. Therefore, a 100.0 g sample of bleach would contain 7.4 g of NaOCl.

Figure 1.4.3. Liquid bleach is an aqueous solution of sodium hypochlorite (NaOCl). This brand has a concentration of 7.4 % NaOCl by mass.

Example 1.4.6 – Calculation of Percent by Mass 

A 5.0 g sample of spinal fluid contains 3.75 mg (0.00375 g) of glucose. What is the percent by mass of glucose in spinal fluid?

Solution

The spinal fluid sample contains roughly 4 mg of glucose in 5000 mg of fluid, so the mass fraction of glucose should be a bit less than one part in 1000, or about 0.1 %. Substituting the given masses into the equation defining mass percentage yields:

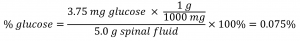
This result compares well to our ballpark estimate.

Check Your Learning 1.4.6 – Calculation of Percent by Mass 

What is the concentration of the solution that results from diluting 25.0 mL of a 2.04 mol/L solution of CH₃OH to 500.0 mL?

Answer

14.8 %

Example 1.4.7 – Calculations using Mass Percentage

“Concentrated” hydrochloric acid is an aqueous solution of 37.2 % HCl by mass that is commonly used as a laboratory reagent. The density of this solution is 1.19 g/mL. What mass of HCl is contained in 0.500 L of this solution?

Solution

The HCl concentration is near 40%, so a 100 g portion of this solution would contain about 40 g of HCl. Since the solution density isn’t greatly different from that of water (1 g/mL), a reasonable estimate of the HCl mass in 500 g (0.5 L) of the solution is about five times greater than that in a 100 g portion, or 5 × 40 = 200 g. In order to derive the mass of solute in a solution from its mass percentage, we need to know the corresponding mass of the solution. Using the solution density given, we can convert the solution’s volume to mass, and then use the given mass percentage to calculate the solute mass. This mathematical approach is outlined in this flow chart:

For proper unit cancellation, the 0.500 L volume is converted into 500 mL, and the mass percentage is expressed as a ratio, 37.2 g HCl/100 g solution, as shown in the dimensional analysis below: :

This mass of HCl is consistent with our rough estimate of approximately 200 g.

Check Your Learning 1.4.7 – Calculations using Mass Percentage

What volume of concentrated HCl solution contains 125 g of HCl?

Answer

V = 282 mL

Volume Percentage

Liquid volumes over a wide range of magnitudes are conveniently measured using common and relatively inexpensive laboratory equipment. The concentration of a solution formed by dissolving a liquid solute in a liquid solvent is therefore often expressed as a volume percentage, % vol or (v/v)%:

Again, any unit for volume may be used as long as it is consistently applied in the numerator and denominator  

Example 1.4.8 – Calculations using Volume Percentage

Rubbing alcohol (isopropanol) is usually sold as a 70 % by volume aqueous solution. If the density of isopropanol is 0.785 g/mL, how many grams of isopropanol are present in a 355 mL bottle of rubbing alcohol?

Solution

Per the definition of volume percentage, the isopropanol volume is 70 % of the total solution volume. In other words, each 100mL of solution contains 70mL of isopropanol. Multiplying the isopropanol volume by its density yields the requested mass:

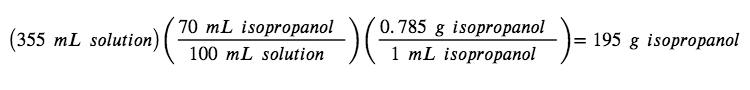
Check Your Learning 1.4.8 – Calculations using Volume Percentage

Wine is approximately 12 % ethanol (CH₃CH₂OH) by volume. Ethanol has a molar mass of 46.06 g/mol and a density 0.789 g/mL. How many moles of ethanol are present in a 750-mL bottle of wine?

Answer

n = 1.5 mol ethanol

Mass-Volume Percentage

“Mixed” percentage units, derived from the mass of solute and the volume of solution, are popular for certain biochemical and medical applications. A mass-volume percent is a ratio of a solute’s mass to the solution’s volume expressed as a percentage. The specific units used for solute mass and solution volume may vary, depending on the solution. For example, a physiological saline solution, used to prepare intravenous fluids, has a concentration of 0.9% mass/volume (m/v), indicating that the composition is 0.9 g of solute per 100 mL of solution. The concentration of glucose in blood (commonly referred to as “blood sugar”) is also typically expressed in terms of a mass-volume ratio. Though not expressed explicitly as a percentage, its concentration is usually given in milligrams of glucose per deciliter (100 mL) of blood (Figure 1.4.4).

Figure 1.4.4. “Mixed” mass-volume units are commonly encountered in medical settings. (a) The NaCl concentration of physiological saline is 0.9% (m/v). (b) This device measures glucose levels in a sample of blood. The normal range for glucose concentration in blood (fasting) is around 70–100 mg/dL. (credit a: modification of work by “The National Guard”/Flickr; credit b: modification of work by Biswarup Ganguly)

Parts per Million and Parts per Billion

Very low solute concentrations are often expressed using appropriately small units such as parts per million (ppm) or parts per billion (ppb).

The mass-based definitions of ppm and ppb are given here:

Both ppm and ppb are convenient units for reporting the concentrations of pollutants and other trace contaminants in water. Concentrations of these contaminants are typically very low in treated and natural waters, and their levels cannot exceed relatively low concentration thresholds without causing adverse effects on health and wildlife. For example, the Environmental Protection Agency (EPA) has identified the maximum safe level of fluoride ion in tap water to be 4 ppm. Inline water filters are designed to reduce the concentration of fluoride and several other trace-level contaminants in tap water (Figure 1.4.5).

Figure 1.4.5. (a) In some areas, trace-level concentrations of contaminants can render unfiltered tap water unsafe for drinking and cooking. (b) Inline water filters reduce the concentration of solutes in tap water. (credit a: modification of work by Jenn Durfey; credit b: modification of work by “vastateparkstaff”/Wikimedia commons)

Example 1.4.9 – Calculation of Parts per Million and Parts per Billion Concentrations

According to the EPA, when the concentration of lead in tap water reaches 15 ppb, certain remedial actions must be taken. What is this concentration in ppm? At this concentration, what mass of lead (μg) would be contained in a typical glass of water (300 mL)?

Solution

The definitions of the ppm and ppb units may be used to convert the given concentration from ppb to ppm. Comparing these two unit definitions shows that ppm is 1000 times greater than ppb (1 ppm = 10³ ppb). Thus: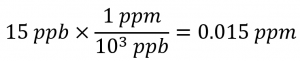

Thus, one million grams of tap water (1 x 10^6 g) contains 0.015g of lead. The definition of the ppb unit may be used to calculate the requested mass if the mass of the solution is provided. However, only the volume of solution (300 mL) is given, so we must use the density to derive the corresponding mass. We can assume the density of tap water to be roughly the same as that of pure water (~1.00 g/mL), since the concentrations of any dissolved substances should not be very large.

Now, we can apply the concentration in dimensional analysis to find the mass of lead in the desired units, µg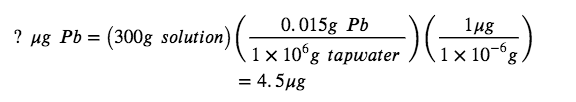 

Check Your Learning 1.4.9 – Calculation of Parts per Million and Parts per Billion Concentrations

(a) Your tap water contains 4.0 ppm fluoride. A conspiracy website says fluoride is dangerous and you can be poisoned if you consume more than 5.0 grams of it. If you drink 6 glasses (each glass is 0.40 L) of tap water per day, how long until you consume 5.0 grams of fluoride (assuming it NEVER leaves your body?).

(b) A 50.0 g sample of industrial wastewater was determined to contain 0.48 mg of mercury. Express the mercury concentration of the wastewater in ppm and ppb units.

  Answer

  a. 520 days

  b. 9.6 ppm, 9600 ppb

Molality

A final way to express the concentration of a solution is by its molality. The molality (b) of a solution is the moles of solute divided by the kilograms of solvent. A solution that contains 1.0 mol of NaCl dissolved into 1.0 kg of water is a “one-molal” solution of sodium chloride. The symbol for molality is a lower-case b written in italics.

Molality differs from molarity only in the denominator. While molarity is based on the litres of solution, molality is based on the kilograms of solvent. Concentrations expressed in molality are used when studying the properties of solutions related to vapour pressure and temperature changes. Molality is used because its value does not change with changes in temperature. The volume of a solution, on the other hand, is slightly dependent upon temperature.

Example 1.4.10 – Molality

Determine the molality of a solution prepared by dissolving 28.60 g of glucose (C₆H₁₂O₆) into 250 g of water.

Solution

Convert grams of glucose to moles and divide by the mass of the water in kilograms:

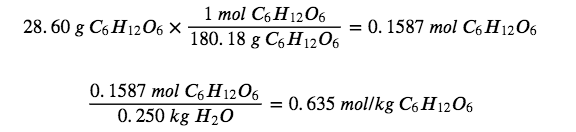
The answer represents the moles of glucose per kilogram of water and has three significant figures.

Molality and molarity are closely related in value for dilute aqueous solutions because the density of those solutions is relatively close to 1.0 g/mL. This means that 1.0 L of solution has nearly a mass of 1.0 kg. As the solution becomes more concentrated, its density will not be as close to 1.0 g/mL and the molality value will be different than the molarity. For solutions with solvents other than water, the molality will be very different than the molarity. Make sure that you are paying attention to which quantity is being used in a given problem.

Water as a Universal Solvent

Water is dubbed a universal solvent because it dissolves many substances due to strong interactions between water molecules and those of other substances. Entropy is another driving force for a liquid to dissolve or mix with other substances (just know for now that entropy describes matter and/or energy dispersal within a system or the measure of the disorder of a system). Mixing increases disorder or entropy. You will learn more about entropy in CHM2131/CHM2132.

Hydrophobic effect and hydrophilic effect

Because of its high dipole moment and ability to donate and accept protons for hydrogen bonding, water is an excellent solvent for polar substances and electrolytes, which consist of ions. Molecules that strongly interact with or love water molecules are hydrophilic, due to hydrogen bonding, polar-ionic or polar-polar attractions. Nonpolar molecules that do not mix with water are hydrophobic or lipophilic because they tend to dissolve in oil. Large molecules such as proteins and fatty acids that have hydrophilic and hydrophobic portions are amphipathic or amphiphilic. Water molecules strongly intermingle with hydrophilic portions by means of dipole-dipole interaction or hydrogen bonding. This will be examined in detail in CHM1321.

Dilution of Solutions

Dilution is the process whereby the concentration of a solution is lessened by the addition of solvent. For example, we might say that a glass of iced tea becomes increasingly diluted as the ice melts. The water from the melting ice increases the volume of the solvent (water) and the overall volume of the solution (iced tea), thereby reducing the relative concentrations of the solutes that give the beverage its taste (Figure 1.4.6).

Figure 1.4.6. Both solutions contain the same mass of copper nitrate. The solution on the right is more dilute because the copper nitrate is dissolved in more solvent. (credit: Mark Ott)

Dilution is also a common means of preparing solutions of a desired concentration. By adding solvent to a measured portion of a more concentrated stock solution, we can achieve a particular concentration. For example, commercial pesticides are typically sold as solutions in which the active ingredients are far more concentrated than is appropriate for their application. Before they can be used on crops, these pesticides must be diluted. This is also a very common practice for the preparation of a number of common laboratory reagents (Figure 1.4.7).

Figure 1.4.7. A solution of KMnO₄ is prepared by mixing water with 4.74 g of KMnO₄ in a flask. (credit: modification of work by Mark Ott)

A simple mathematical relationship can be used to relate the volumes and concentrations of a solution before and after the dilution process. According to the definition of molarity, the molar amount of solute in a solution (n) is equal to the product of the solution’s molarity (M) and its volume in litres (V):

n = MV

Expressions like these may be written for a solution before and after it is diluted:

n₁ = M₁V₁

n₂ = M₂V₂

where the subscripts “1” and “2” refer to the solution before and after the dilution, respectively. Since the dilution process does not change the amount of solute in the solution, n₁ = n₂. Thus, these two equations may be set equal to one another:

M₁ V₁ = M₂ V₂

This relation is commonly referred to as the dilution equation. Although we derived this equation using molarity as the unit of concentration and litres as the unit of volume, other units of concentration and volume are more commonly used. The dilution equation is often written in the more general form:

C₁ V₁ = C₂ V₂

where C and V are the solution’s concentration and volume respectively.

Example 1.4.11 – Determining the Concentration of a Diluted Solution

If 0.850 L of a 5.00 mol/L solution of copper nitrate, Cu(NO₃)₂, is diluted to a volume of 1.80 L by the addition of water, what is the molarity of the diluted solution?

Solution

We are given the volume and concentration of a stock solution, V₁ and C₁, and the volume of the resultant diluted solution, V₂. We need to find the concentration of the diluted solution, C₂. We thus rearrange the dilution equation in order to isolate C₂:

Since the stock solution is being diluted by more than two-fold (volume is increased from 0.85 L to 1.80 L), we would expect the diluted solution’s concentration to be less than one-half of 5 mol/L. We will compare this ballpark estimate to the calculated result to check for any gross errors in computation (for example, such as an improper substitution of the given quantities). Substituting the given values for the terms on the right side of this equation yields:

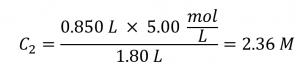
This result compares well to our ballpark estimate (it’s a bit less than one-half the stock concentration, 5 mol/L).

Check Your Learning 1.4.11 – Determining the Concentration of a Diluted Solution

What is the concentration of the solution that results from diluting 25.0 mL of a 2.04 mol/L solution of CH₃OH to 500.0 mL?

Answer

0.102 mol/L CH₃OH

Example 1.4.12 – Volume of a Diluted Solution

What volume of 0.12 mol/L HBr can be prepared from 11 mL (0.011 L) of 0.45 mol/L HBr?

Solution

We are given the volume and concentration of a stock solution, V₁ and C₁, and the concentration of the resultant diluted solution, C₂. We need to find the volume of the diluted solution, V₂. We thus rearrange the dilution equation in order to isolate V₂:

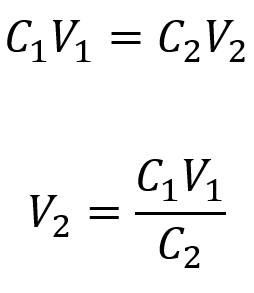
Since the diluted concentration (0.12 mol/L) is slightly more than one-fourth of the original concentration (0.45 mol/L), we would expect the volume of the diluted solution to be roughly four times the original volume, around 44 mL. Substituting the given values and solving for the unknown volume yields:

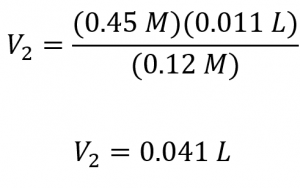
The volume of the 0.12 mol/L solution is 0.041 L (41 mL). The result is reasonable and compares well with our rough estimate.

Check Your Learning 1.4.10 – Volume of a Diluted Solution

A laboratory experiment calls for 0.125 mol/L HNO₃. What volume of 0.125 mol/L HNO₃ can be prepared from 0.250 L of 1.88 mol/L HNO₃?

Answer

V = 3.76 L

Example 1.4.13 – Volume of a Concentrated Solution Needed for Dilution

What volume of 1.59 mol/L KOH is required to prepare 5.00 L of 0.100 mol/L KOH?

Solution

We are given the concentration of a stock solution, C₁, and the volume and concentration of the resultant diluted solution, V₂ and C₂. We need to find the volume of the stock solution, V₁. We thus rearrange the dilution equation in order to isolate V₁: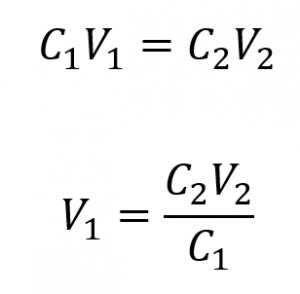

Since the concentration of the diluted solution 0.100 mol/L is roughly one-sixteenth that of the stock solution (1.59 mol/L), we would expect the volume of the stock solution to be about one-sixteenth that of the diluted solution, or around 0.3 litres. Substituting the given values and solving for the unknown volume yields:

Thus, we would need 0.314 L of the 1.59 mol/L solution to prepare the desired solution. This result is consistent with our rough estimate.

Check Your Learning 1.4.11 – Volume of a Concentrated Solution Needed for Dilution

What volume of a 0.575 mol/L solution of glucose, C₆H₁₂O₆, can be prepared from 50.00 mL of a 3.00 mol/L glucose solution?

  Answer

V = 0.261 L

Molecular, Complete Ionic, and Net Ionic Equations

So far, we have looked only at molecular equations. These are the balanced reaction equations where we have accounted for all the atoms involved in the reaction. For some reactions, this isn’t the whole story. In the cases where we have ionic compounds dissolved in water, we need to go one step further.

Let us consider the precipitation reaction for the formation of barium sulfate. Precipitation is a process in which a homogeneous solution reacts to form a solid product (known as the precipitate) The complete chemical equation for this reaction can be written to describe what happens, and such an equation is useful in making chemical calculations: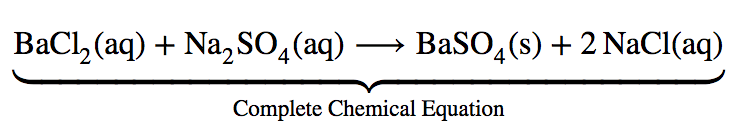

However, the complete chemical equation does not really represent the microscopic particles (that is, the ions) present in the solution. Thus we might write below the complete ionic equation, where the aqueous salts are written as their individual ions: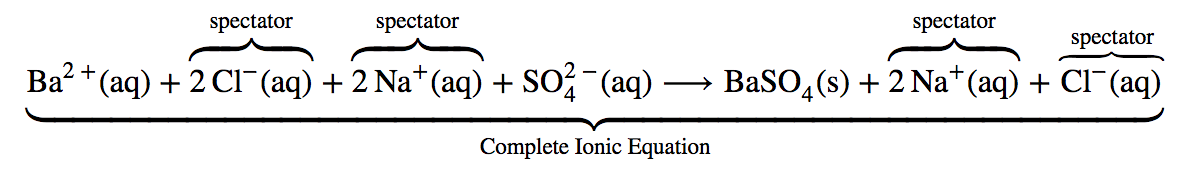

The complete ionic equation is rather cumbersome and includes so many different ions that it may be confusing. In any case, we are often interested in the independent behaviour of ions, not the specific compound from which they came. A precipitate of BaSO₄ (s) will form when any solution containing Ba²⁺(aq) is mixed with any solution containing SO₄^2– (aq) (provided concentrations are not extremely small). This happens independently of the Cl^– (aq) and Na⁺ (aq) ions in the complete ionic equation. These ions are called spectator ions because they do not participate in the reaction. When we want to emphasize the independent behaviour of ions, a net ionic equation is written, omitting the spectator ions. For precipitation of BaSO_4, the net ionic equation is”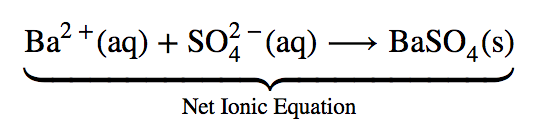

Example 1.4.14 – AgCl Precipitation

When a solution of AgNO₃ is added to a solution of CaCl₂, insoluble AgCl precipitates. Write three equations (complete chemical equation, complete ionic equation, and net ionic equation) that describe this process.

Solution

Complete Chemical Equation:

2 AgNO₃ (aq) + CaCl₂ (aq)  →  2 AgCl (s) + Ca(NO₃)₂ (aq)

The proper states and formulas of all products are written and the chemical equation is balanced.

Complete Ionic Equation:

Net Ionic Equation:

All spectator ions are removed.

Check Your Learning 1.4.12 – SrCO₃ Precipitation

Write balanced net ionic equations to describe the formation of solid strontium carbonate that occurs when K₂CO₃ and SrCl₂ are mixed.

Answer

Sr²⁺ (aq) + CO₃^2- (aq) → SrCO₃ (s)

Check Your Learning 1.4.13 – BaSO₄ Precipitation 

Write a balanced net ionic equation to describe to describe the formation of solid barium sulfate which occurs when aqueous FeSO₄ and Ba(NO₃)₂ are mixed.

Answer

Ba²⁺ (aq) + SO₄^2- (aq) → BaSO₄ (s)

The occurrence or nonoccurrence of precipitates can be used to detect the presence or absence of various species in solution. A BaCl₂ solution, for instance, is often used as a test for the presence of SO₄^2- ions. There are several insoluble salts of Ba, but they all dissolve in dilute acid except for BaSO₄. Thus, if BaCl₂ solution is added to an unknown solution that has previously been acidified, the occurrence of a white precipitate is proof of the presence of the SO₄^2- ion.

AgNO₃ solutions are often used in a similar way to test for halide ions. If an AgNO₃ solution is added to an acidified unknown solution, a white precipitate indicates the presence of Cl^– ions, a cream-coloured precipitate indicates the presence of Br^– ions, and a yellow precipitate indicates the presence of I^– ions (Figure 1.4.8). Further tests can then be made to see whether perhaps a mixture of these ions is present. When AgNO₃ is added to tap water, a white precipitate is almost always formed. The Cl^– ions in tap water usually come from the Cl₂ which is added to municipal water supplies to kill microorganisms.

Figure 1.4.8. The three common silver halide precipitates: AgI, AgBr and AgCl (left to right). The silver halides precipitate out of solution, but often form suspensions before settling. Image used with permission (CC BY-SA 3.0; Cychr).

Precipitates are also used for quantitative analysis of solutions, that is, to determine the amount of solute or the mass of solute in a given solution. For this purpose, it is often convenient to use the first of the three types of equations described above. Then the rules of stoichiometry may be applied. Prediction of precipitation reactions will be examined in further detail in Chapter 6.  

★ Questions

1. Determine the molarity for each of the following solutions:

(a) 0.444 mol of CoCl₂ in 0.654 L of solution

(b) 98.0 g of phosphoric acid, H₃PO₄, in 1.00 L of solution

(c) 0.2074 g of calcium hydroxide, Ca(OH)₂, in 40.00 mL of solution

(d) 10.5 kg of Na₂SO₄·10H₂O in 18.60 L of solution

(e) 7.0 × 10⁻³ mol of I₂ in 100.0 mL of solution

(f) 1.8 × 10⁴ mg of HCl in 0.075 L of solution

2. What is the mass of the solute in 0.500 L of 0.30 M glucose, C₆H₁₂O₆, used for intravenous injection? Outline the steps necessary to answer the question.

3. Calculate the number of moles and the mass of the solute in each of the following solutions:

(a) 2.00 L of 18.5 mol/L H₂SO₄, concentrated sulfuric acid

(b) 100.0 mL of 3.8 × 10⁻⁵ mol/L NaCN, the minimum lethal concentration of sodium cyanide in blood serum

(c) 5.50 L of 13.3 mol/L H₂CO, the formaldehyde used to “fix” tissue samples

(d) 325 mL of 1.8 × 10⁻⁶ mol/L FeSO₄, the minimum concentration of iron sulfate detectable by taste in drinking water

4. What is the molarity of KMnO₄ in a solution of 0.0908 g of KMnO₄ in 0.500 L of solution? Outline the steps necessary to answer the question.

5. Calculate the molarity of each of the following solutions:

(a) 0.195 g of cholesterol, C₂₇H₄₆O, in 0.100 L of serum, the average concentration of cholesterol in human serum

(b) 4.25 g of NH₃ in 0.500 L of solution, the concentration of NH₃ in household ammonia

(c) 1.49 kg of isopropyl alcohol, C₃H₇OH, in 2.50 L of solution, the concentration of isopropyl alcohol in rubbing alcohol

(d) 0.029 g of I₂ in 0.100 L of solution, the solubility of I₂ in water at 20 °C

6. There is about 1.0 g of calcium, as Ca²⁺, in 1.0 L of milk. What is the molarity of Ca²⁺ in milk?

7. A 9.00 g sample contains 45.0 mg of dissolved sugar. What is the percent by mass of sugar in this solution?

★★ Questions

8. A cleaning solution is 4% by mass sodium hypochlorite (bleach). If you use 70 g of cleaning solution to clean your bathroom, how much bleach was used?

9. Your beer is 7% alcohol by volume. How much pure alcohol did you actually drink if your bottle contains 7 fl oz and you have had two and a half bottles?

10. You mix 73 μL of loading dye with 1000 μL of DNA. How much loading dye is there in the solution by volume percent.

11. Your blood sugar reading is 0.2% (m/v). How many grams of sugar are in your body (assuming you contain 5.1 L of blood)?

12. Suppose the vinegar you use is 0.76 mol/L acetic acid (CH₃COOH). What is the concentration of your vinegar in ppm?

13. Suppose you mix 50 mL CoCl₂ in 0.654 L of solution. What is the concentration of the resulting mixture in ppb?

14. You add 3.6 g of H₂SO₄ to 10.0 g of water. What is the molality of this solution?

15. You have 1 L of saline solution (NaCl) at 0.15 mol/L. What is the molality of the solution if NaCl has a density of 2.16 g/cm³ (hint: 1 cm³ = 1 mL)?

16. If 4.12 L of a 0.850 mol/L H₃PO₄ solution is diluted to a volume of 10.00 L, what is the concentration of the resulting solution?

★ Questions (Part 2)

17. What is the final concentration of the solution produced when 225.5 mL of a 0.09988 mol/L solution of Na₂CO₃ is allowed to evaporate until the solution volume is reduced to 45.00 mL?

18. An experiment in a general chemistry laboratory calls for a 2.00 mol/L solution of HCl. How many mL of 11.9 mol/L HCl would be required to make 250 mL of 2.00 mol/L HCl?

19. Write out the complete chemical equation, complete ionic equation, and net ionic equation for the mixture of Ca(NO₃)₂ (aq) and H₃PO₄ (aq)  to form solid calcium phosphate.

20. Write out the complete chemical equation, complete ionic equation, and net ionic equation for the mixture of KCl (aq) and Pb(NO₃)₂ (aq) to form solid lead (II) chloride.

Answers

1. (a) 0.679 mol/L; (b) 1.00 mol/L; (c) 0.06998 mol/L; (d) 1.75 mol/L; (e) 0.070 mol/L; (f) 6.6 mol/L

2. 27 g; Determine the number of moles of glucose in 0.500 L of solution; determine the molar mass of glucose; determine the mass of glucose from the number of moles and its molar mass.

3. (a) 37.0 mol H₂SO₄; 3.63 x 10³ g H₂SO₄; (b) 3.8 × 10⁻⁶ mol NaCN; 1.9 × 10⁻⁴ g NaCN; (c) 73.2 mol H₂CO; 2.20 kg H₂CO; (d) 5.9 × 10⁻⁷ mol FeSO₄; 8.9 × 10⁻⁵ g FeSO₄

4. 1.15 × 10⁻³ mol/L; Determine the molar mass of KMnO₄; determine the number of moles of KMnO₄ in the solution; from the number of moles and the volume of solution, determine the molarity.

5. (a) 5.04 × 10⁻³ mol/L; (b) 0.499 mol/L; (c) 9.92 mol/L; (d) 1.1 × 10⁻³ mol/L

6. 0.025 mol/L

7. 0.5%

8. 2.8 g

9. 36.23 mL

10. 6.8%

11. 1.02 kg

12. 45719.97 ppm

13. 71 022 727 ppb

14. 3.67 mol/kg

15. 0.069 mol/kg

16. 0.35 mol/L

17. 0.50 mol/L

18. 42 mL

19. Complete: 3 Ca(NO₃)₂ + 2 H₃PO₄  →  Ca₃(PO₄)₂ + 6 HNO₃

Complete Ionic: 3 Ca²⁺+ 6 NO₃^– + 6 H + 2 PO₄^3-  →  Ca₃(PO₄)₂ + 6 H + 6 NO₃^–

Net Ionic: 3 Ca²⁺ + 2 PO₄^3-  →  Ca₃(PO₄)₂

20. Complete: Pb(NO₃)₂ (aq) + 2 KI (aq)  →  PbI₂ (s) + 2 KNO₃ (aq)

Complete Ionic: Pb²⁺ (aq) + 2 NO₃^–(aq) + 2 K⁺ (aq) + 2 I^– (aq)  →  PbI₂ (aq) + 2 K⁺ (aq) + 2 NO₃^–(aq)

Net Ionic: Pb²⁺ (aq) + 2 I^– (aq)  →  PbI₂ (aq)