2.3 – Measuring Variables of Gases
Pressure
Any object, whether it is your computer, a person, or a sample of gas, exerts a force on any surface with which it comes in contact. The air in a balloon, for example, exerts a force against the interior surface of the balloon, and a liquid injected into a mold exerts a force against the interior surface of the mold, just as a chair exerts a force against the floor because of its mass and the effects of gravity. If the air in a balloon is heated, the increased kinetic energy of the gas eventually causes the balloon to burst because of the increased pressure (P) of the gas, the applied force (F) per unit area (A) of surface:
![]()
Equation 2.3.1. The pressure force area relation.
Pressure is dependent on both the force exerted and the size of the area to which the force is applied. We know from the equation relating force, area, and pressure that applying the same force to a smaller area produces a higher pressure. When we use a hose to wash a car, for example, we can increase the pressure of the water by reducing the size of the opening of the hose with a thumb.
The units of pressure are derived from the units used to measure force and area. The SI unit for pressure, derived from the SI units for force (newtons) and area (square metres), is the newton per square metre (N/m2), which is called the Pascal (Pa), after the French mathematician Blaise Pascal (1623 – 1662):
1 Pa = 1 N/m2
One pascal is a very small pressure; in many cases, it is more convenient to use units of kilopascal (1 kPa = 1000 Pa) or bar (1 bar = 100 000 Pa).
Example 2.3.1 – Pressure Exerted by a Textbook
Assuming a textbook has a mass of 2.00 kg, a length of 27.0 cm, a width of 21.0 cm, and a thickness of 4.5 cm, what pressure does it exert on a surface if it is:
(a) lying flat?
(b) standing on edge in a bookcase?
Solution
The force exerted by the book does not depend on its orientation. Recall that the force exerted by an object is F = ma, where m is its mass and a is its acceleration. In Earth’s gravitational field, the acceleration is due to gravity (9.8067 m/s2 at Earth’s surface). In SI units, the force exerted by the book is therefore:![]()
(a) We calculated the force as 19.6 N. When the book is lying flat, the area is:
A = 0.270 m × 0.210 m = 0.0567 m2
The pressure exerted by the text lying flat is thus:
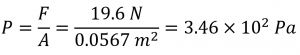
b) If the book is standing on its end, the force remains the same, but the area decreases:
A = 21.0 cm × 4.5 cm = 0.210 m × 0.045 m = 9.5 × 10-3 m2
The pressure exerted by the text standing on its end is thus:
![]()
Check Your Learning 2.3.1 – Pressure Exerted by a Student
What pressure does a 60.0 kg student exert on the floor:
(a) when standing flat-footed in the laboratory in a pair of tennis shoes (the surface area of the soles is approximately 180 cm2)?
(b) as she steps heel-first onto a dance floor wearing high-heeled shoes (the area of the heel = 1.0 cm2)?
Answer
(a) 3.27 × 104 Pa
(b) 5.9 × 106 Pa
Atmospheric Pressure
The air surrounding the earth is pulled toward the surface by gravity in the same way as the paperback book in the example above. Consequently, the air also exerts a pressure on the surface. This is called atmospheric pressure.
The following video shows the ‘power’ of atmospheric pressure. A metal can full of water is heated until the water inside boils, creating a high internal pressure. The can is then put upside down into a bowl of cold ice water, causing the formerly hot water vapour to cool and decrease in volume. This cooling causes a decrease in the internal pressure of the can. The lower pressure exerts less force on the can and can no longer counter the atmospheric pressure coming from the outside of the can, which pushes inward, crushing the can. This can also be seen in Figure 2.3.1 on a much larger scale.

Figure 2.3.1. In this GIF, Thomas the railroad tank car is crushed by the difference in pressure between its evacuated interior and external atmospheric pressure.
Because winds may add more air or take some away from the vertical column above a given area on the surface, atmospheric pressure will vary. Pressure also decreases as one moves to higher altitudes. The tops of the Himalayas, the highest mountains in the world at about 8000 m (almost 5 miles), are above more than half the atmosphere. The lower pressure at such heights makes breathing very difficult—even the slightest exertion leaves one panting and weak. For this reason, jet aircraft, which routinely fly at altitudes of 8 to 10 km, have equipment to maintain air pressure in their cabins artificially.
It is often convenient to express pressure using a unit which is about the same as the average atmospheric pressure at sea level. Atmospheric pressure is about 101 kPa, and the standard atmosphere (atm) is defined as exactly 101.325 kPa. Since this unit is often used, it is useful to remember that:
1 atm = 101.325 kPa = 1.01325 bar
Example 2.3.2 – Atmospheric Pressure
The total mass of air directly above a 30 cm by 140 cm section of the Atlantic Ocean was 4.34 × 103 kg on July 27, 1977. Calculate the pressure exerted on the surface of the water by the atmosphere.
Solution
First calculate the force of gravitational attraction on the air:
F = ma = (4.34 × 103 kg) × (9.81 m⋅s-2) = 4.26 × 104 kg⋅m⋅s-2 = 4.26 × 104 N
The area is:
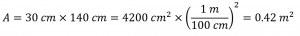
Thus the pressure is:
![]()
Barometric Pressure
Just as we exert pressure on a surface because of gravity, so does our atmosphere. We live at the bottom of an ocean of gases that becomes progressively less dense with increasing altitude. Approximately 99% of the mass of the atmosphere lies within 30 km of Earth’s surface (Figure 2.3.2). Every point on Earth’s surface experiences a net pressure called barometric pressure. The pressure exerted by the atmosphere is considerable: a 1 m2 column, measured from sea level to the top of the atmosphere, has a mass of about 10 000 kg, which gives a pressure of about 101 kPa. However, we typically do not perceive this pressure because we are physiologically adapted to it!
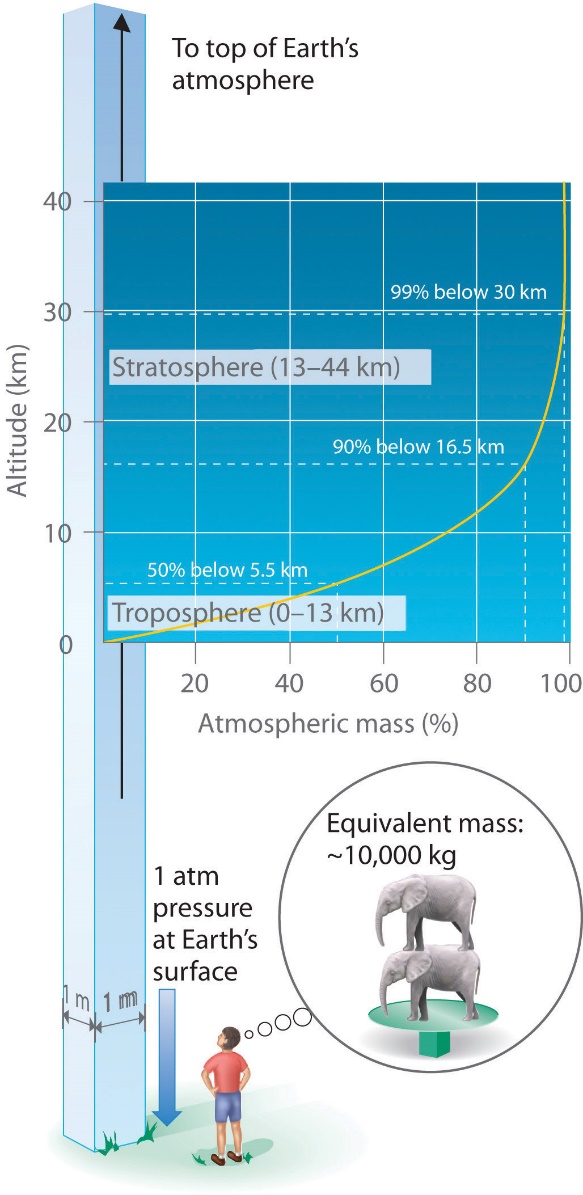
Figure 2.3.2. Barometric pressure. Each square metre of Earth’s surface supports a column of air that is more than 200 km high and weighs about 10 000 kg at Earth’s surface.
Barometric pressure can be measured using a barometer, a device invented in 1643 by one of Galileo’s students, Evangelista Torricelli (1608–1647). As shown in Figure 2.3.3, a barometer may be constructed from a long glass tube that is closed at one end. It is filled with mercury and placed upside down in a dish of mercury without allowing any air to enter the tube. Some of the mercury will run out of the tube, but a relatively tall column remains inside. Why doesn’t all the mercury run out? Gravity is certainly exerting a downward force on the mercury in the tube, but it is opposed by the pressure of the atmosphere pushing down on the surface of the mercury in the dish, which has the net effect of pushing the mercury up into the tube. Because there is no air above the mercury inside the tube in a properly filled barometer (it contains a vacuum), there is no pressure pushing down on the column. Thus, the mercury runs out of the tube until the pressure exerted by the mercury column itself exactly balances the pressure of the atmosphere. The pressure exerted by the mercury column can be expressed as:
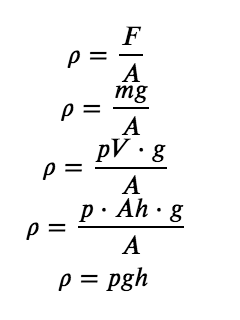
with g is the gravitational acceleration, m is the mass, ρ is the density, V is the volume, A is the bottom area, and h is the height of the mercury column.
Under normal weather conditions at sea level, the two forces are balanced when the top of the mercury column is approximately 760 mm above the level of the mercury in the dish, as shown in Figure 2.3.3. This value varies with meteorological conditions and altitude. In Denver, Colorado, for example, at an elevation of about 1 mile, or 1609 m (5280 ft), the height of the mercury column is 630 mm rather than 760 mm.

Figure 2.3.3. A mercury barometer. The pressure exerted by the atmosphere on the surface of the pool of mercury supports a column of mercury in the tube that is about 760 mm tall. Because the boiling point of mercury is quite high (356.73 °C), there is negligible mercury vapour in the space above the mercury column.
Mercury barometers have been used to measure barometric pressure for so long that they have their own unit for pressure: the millimetre of mercury (mmHg), often called the Torr, after Torricelli. Standard barometric pressure is the barometric pressure required to support a column of mercury exactly 760 mm tall; this pressure is also referred to as 1 atmosphere (atm). These units are also related to the pascal:
1 atm = 760 mmHg
= 760 Torr
= 1.01325 × 105 Pa
= 101.325 kPa
= 1.01325 bar
= 14.6959 psi
Thus, a pressure of 1 atm equals 760 mmHg exactly.
We are so accustomed to living under this pressure that we never notice it. Instead, what we notice are changes in the pressure, such as when our ears pop in fast elevators in skyscrapers or in airplanes during rapid changes in altitude. We make use of barometric pressure in many ways. We can use a drinking straw because sucking on it removes air and thereby reduces the pressure inside the straw. The barometric pressure pushing down on the liquid in the glass then forces the liquid up the straw.
To learn more about the barometer and its history, check out the following video.
Example 2.3.3 – Barometric Pressure
A general chemistry professor visited Rocky Mountain National Park several years ago. After departing from an airport at sea level in the eastern United States, he arrived in Denver (altitude 5280 ft), rented a car, and drove to the top of the highway outside Estes Park (elevation 14 000 ft). He noticed that even slight exertion was very difficult at this altitude, where the barometric pressure is only 454 mmHg. Convert this pressure to:
(a) atmospheres (atm).
(b) bar.
Solution
(a) From the conversion factors, we have 1 atm = 760 mmHg = 101.325 kPa. The pressure at 14,000 ft in atm is thus:
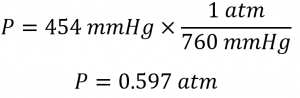
(b) The pressure in bar is given by:
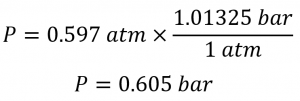
Check Your Learning 2.3.2 – Barometric Pressure
Mt. Everest, at 29,028 ft above sea level, is the world’s tallest mountain. The normal barometric pressure at this altitude is about 0.308 atm. Convert this pressure to:
(a) Millimetres of mercury
(b) Bar
(c) Pascals
Answer
(a) 234 mmHg
(b) 0.312 bar
(c) 31 200 Pa
Manometers
Barometers measure barometric pressure, but manometers measure the pressures of samples of gases contained in an apparatus. The key feature of a manometer is a U-shaped tube containing mercury (or occasionally another nonvolatile liquid). A closed-end manometer is shown schematically in Figure 2.3.4(a). When the bulb contains no gas (i.e., when its interior is a near vacuum), the heights of the two columns of mercury on either side of the U shape are identical because the space above the mercury on the left is also a near vacuum (it contains only traces of mercury vapour). If a gas is added to the bulb on the right, it will exert a pressure on the mercury in the right column, and the two columns of mercury will no longer be the same height. The difference between the heights of the two columns is equal to the pressure of the gas. If the tube is open to the atmosphere instead of closed, as in the open-end manometer shown in Figure 2.3.4(b). then the two columns of mercury have the same height only if the gas in the bulb has a pressure equal to the barometric pressure. If the gas in the bulb has a higher pressure, the mercury in the open tube will be forced up by the gas pushing down on the mercury in the other arm of the U-shaped tube. The pressure of the gas in the bulb is therefore the sum of the barometric pressure (measured with a barometer) and the difference in the heights of the two columns. If the gas in the bulb has a pressure less than that of the atmosphere, then the height of the mercury will be greater in the arm attached to the bulb. In this case, the pressure of the gas in the bulb is the barometric pressure minus the difference in the heights of the two columns.
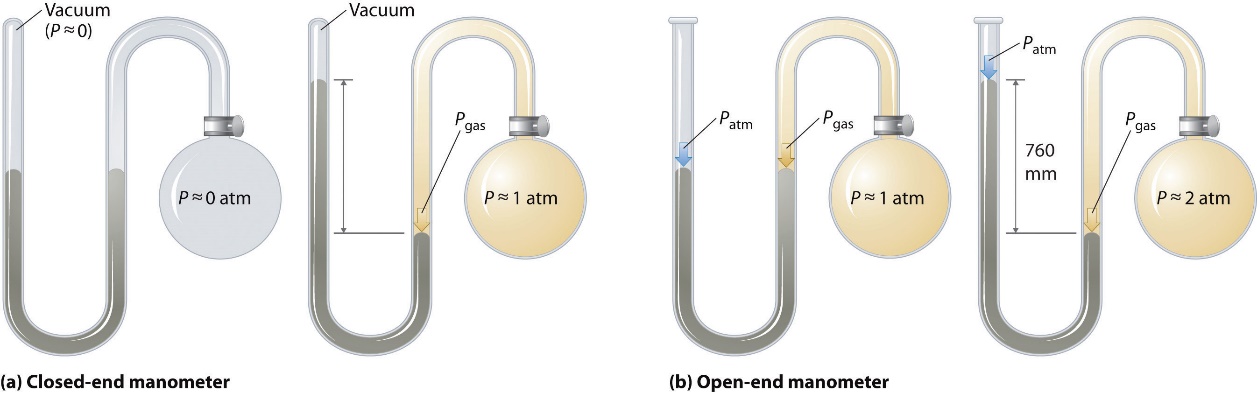
Figure 2.3.4. The two types of manometers. (a) In a closed-end manometer, the space above the mercury column on the left (the reference arm) is essentially a vacuum (P ≈ 0), and the difference in the heights of the two columns gives the pressure of the gas contained in the bulb directly. (b) In an open-end manometer, the left (reference) arm is open to the atmosphere (P ≈ 1 atm), and the difference in the heights of the two columns gives the difference between barometric pressure and the pressure of the gas in the bulb.
To learn more about manometers, check out the following video.
Example 2.3.4 – Applying Theories: Barometers and Manometers
Suppose you want to construct a closed-end manometer to measure gas pressures in the range 0.000–0.200 atm. Because of the toxicity of mercury, you decide to use water rather than mercury. How tall a column of water do you need? (The density of water is 1.00 g/cm3; the density of mercury is 13.53 g/cm3.)
Solution
In millimetres of mercury, a gas pressure of 0.200 atm is:
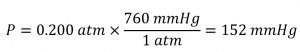
Using a mercury manometer, you would need a mercury column at least 152 mm high.
Because water is less dense than mercury, you need a taller column of water to achieve the same pressure as a given column of mercury. The height needed for a water-filled column corresponding to a pressure of 0.200 atm is proportional to the ratio of the density of mercury to the density of water:
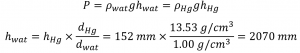
The answer makes sense: it takes a taller column of a less dense liquid to achieve the same pressure.
Check Your Learning 2.3.3 – Applying Theories: Barometers and Manometers
Suppose you want to design a barometer to measure barometric pressure in an environment that is always hotter than 30 °C. To avoid using mercury, you decide to use gallium, which melts at 29.76 °C; the density of liquid gallium at 25 °C is 6.114 g/cm3. How tall a column of gallium do you need if P = 1.00 atm?
Answer
1.68 m
Check Your Learning 2.3.4 – Applying Theories: Barometers and Manometers
Consider the following open-end manometer. What can be concluded about the pressure of the gas within bulb (a)? Bulb (b)?
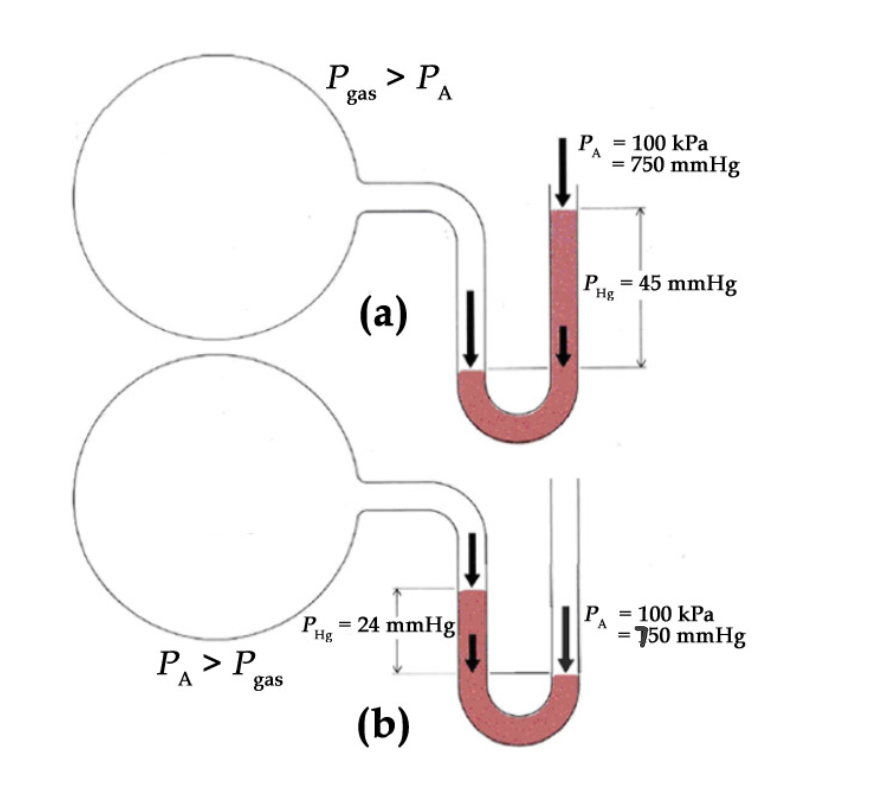
Answer
For bulb (a), the mercury has gone up the right-hand side of the column, indicating that the pressure of the gas is greater than the externally applied pressure, by 45 mmHg:
𝑃𝑔𝑎𝑠 (𝑎)=𝑃𝐴+∆ℎ =750 𝑚𝑚𝐻𝑔 +45 𝑚𝑚𝐻𝑔= 795 𝑚𝑚𝐻𝑔
∴𝑃𝑔𝑎𝑠 (𝑎)= (795 𝑚𝑚𝐻𝑔)(101.325 𝑘𝑃𝑎/ 760 𝑚𝑚𝐻𝑔)= 106 𝑘𝑃𝑎
For bulb (b), the mercury has gone up the left-hand side of the column, indicating that the pressure of the gas is lesser than the externally applied pressure, by 24 mmHg:
𝑃𝑔𝑎𝑠 (𝑏)= 𝑃𝐴 –∆ℎ= 750 𝑚𝑚𝐻𝑔 −24 𝑚𝑚𝐻𝑔= 726 𝑚𝑚𝐻𝑔
∴𝑃𝑔𝑎𝑠 (𝑏)= (726 𝑚𝑚𝐻𝑔)(101.325 𝑘𝑃𝑎/760 𝑚𝑚𝐻𝑔)= 96.8 𝑘𝑃𝑎
The formula derived in Example 2.3.4 can also assist us in other areas, like hydrogeology. For example, consider the problem of building a well to obtain water from an underground aquifer. We can apply a similar method to determine the maximum depth of a well if a simple suction pump will be used to get the water out. A 1.00 atm external barometric pressure would therefore correspond to a maximum water column height of:
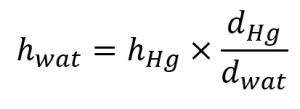
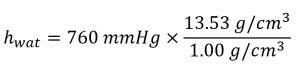
![]()
![]()
A suction pump is just a more sophisticated version of a straw: it creates a vacuum above a liquid and relies on barometric pressure to force the liquid up a tube. If 1.00 atm barometric pressure corresponds to a 10.3 m (33.8 ft) column of water, then it is physically impossible for barometric pressure to raise the water in a well higher than this. Until electric pumps were invented to push water mechanically from greater depths, this factor greatly limited where people could live because obtaining water from wells deeper than about 33 ft was difficult.
Volume
Volume is defined as length times width times height, so it has units of metre × metre × metre or metre3 (m3), sometimes spoken as ‘cubic metres’. The cubic metre is a rather large unit, however, so another unit is defined that is somewhat more manageable: the litre (L). A litre is 1/1000th (1 x 10–3 m3) of a cubic metre and is a little more than 1 quart in volume (Figure 2.3.5.). Prefixes can also be used with the litre unit, so we can speak of millilitres (1 mL = 1 x 10–3 L = 1 x 10–6 m3), microlitres (1 µL = 1 x 10–6 L = 1 x 10–9 m3), and so forth.
Another definition of a litre is one-tenth of a metre cubed. Because one-tenth of a metre is 10 cm, then a litre is equal to 1000 cm3 (Figure 2.3.5). Because 1 L equals 1000 mL, we conclude that 1 mL equals 1 cm3; thus, these units are interchangeable.

Figure 2.3.5. The size of 1 litre. One litre equals 1 000 cm3, so 1 cm3 is the same as 1 mL.
One of the fundamental quantities in science is temperature, which is a measure of the average amount of energy of motion, or kinetic energy, a system contains. Temperatures are expressed using scales that use units called degrees. There are three scales used for reporting temperatures. Figure 2.3.6. compares the three temperature scales.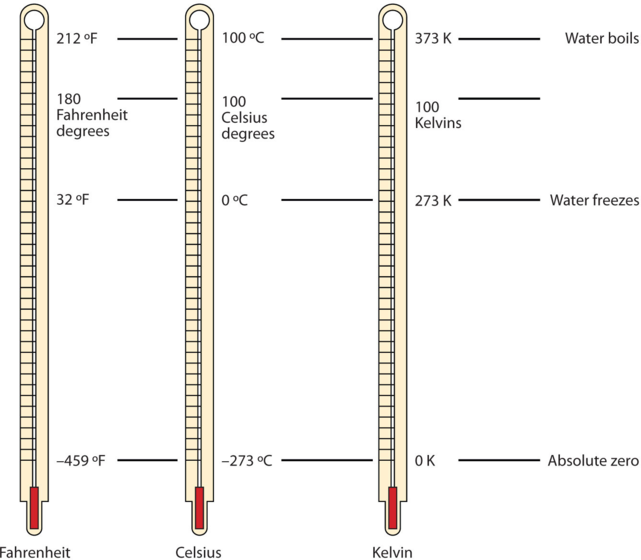
Figure 2.3.6. Fahrenheit, Celsius, and Kelvin temperatures. A comparison of the three temperature scales. These thermometers have a red-colored liquid which contains alcohol and food coloring. Silver-looking thermometers contain mercury, which is a neurotoxin.
Scientists use the Celsius scale (symbolized by °C and spoken as “degrees Celsius”) which defines 0 °C as the freezing point of water and 100 °C as the boiling point of water. This scale is divided into 100 divisions between these two landmarks and extended higher and lower as well. In the United States, the commonly used temperature scale is the Fahrenheit scale (symbolized by °F and spoken as “degrees Fahrenheit”). On this scale, the freezing point of liquid water (the temperature at which liquid water turns to solid ice) is 32 °F, and the boiling point of water (the temperature at which liquid water turns to steam) is 212 °F. By comparing the Fahrenheit and Celsius scales, a conversion between the two scales can be determined:

Note that science uses the Celsius and Kelvin scales almost exclusively; virtually no practicing chemist expresses laboratory-measured temperatures with the Fahrenheit scale, but it is included here for the sake of completeness.
The fundamental unit of temperature in SI is the Kelvin (K). The Kelvin temperature scale (note that the name of the scale capitalizes the word Kelvin, but the unit itself is lowercase) uses degrees that are the same size as the Celsius degree, but the numerical scale is shifted up by 273.15 units. That is, the conversion between the Kelvin and Celsius scales is as follows:
K = ∘C + 273.15
For most purposes, it is acceptable to use 273 instead of 273.15 when converting to Kelvin.
Note that the Kelvin scale does not use the word degrees; a temperature of 295 K is spoken of as “two hundred ninety-five kelvin” and not “two hundred ninety-five degrees kelvin.”
The reason that the Kelvin scale is defined this way is that there exists a minimum possible temperature called absolute zero (zero kelvin). The Kelvin temperature scale is set so that 0 K is absolute zero, and the temperature is counted upward from there. Normal room temperature is about 295 K, as seen in the following example.
Example 2.3.5 – Room Temperature
If the normal room temperature is 72.0 °F, what is room temperature in degrees Celsius and Kelvin?
Solution
First, we determine the temperature in degrees Celsius:
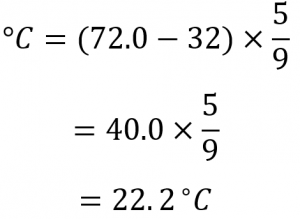
Then we determine the temperature in the Kelvin scale:
K= 22.2 ∘C + 273.15
K= 295.4 K
So, the room temperature is about 295 K.
★ Questions
1. A scuba tank is filled before a dive with air until the pressure gauge reads 200.0 bar. Convert this pressure to:
(a) atm
(b) Pa and kPa
(c) mmHg
2. A round bottom flask with a diameter of 17.0 cm contains 1.00 mol of hydrogen gas at a pressure of 333 Torr. What is the force, in Newtons, exerted on the interior walls of the flask?
3. A cubic container measuring 40.0 cm x 40.0 cm x 40.0 cm weighs 255.0 g when evacuated (empty). When filled with some xenon gas, the pressure generated by the weight of the container on its bottom face is measured to be 21.65 kPa. What amount of xenon gas, in moles, is in the container?
4. Barometric pressure is directly related to meteorological conditions: a stable, high barometric pressure indicates good weather, whereas a falling pressure warns that a low pressure system, bringing poor weather, is approaching. Over the course of an afternoon, the barometric pressure above Ottawa drops from 102.27 kPa to 99.85 kPa. What is the change in the amount of applied force (in Newtons) on the surface of a 1.5 m x 2.5 m picnic table, as the atmospheric pressure drops?
5. On the Canadian Red Cross website, you can find the following advice for what to do if you fall through the ice on a frozen body of water:
“Reach forward onto the broken ice without pushing down. Kick your legs to try to get your body into a horizontal position. Continue kicking your legs, and crawl onto the ice. When you are back on the ice, crawl on your stomach or roll away from the open area with your arms and legs spread out as far as possible. Do not stand up! Look for shore and make sure you are crawling in the right direction.”
Why is it important to crawl or roll away from the open area, instead of standing up and walking away quickly?
6. Barometers and manometers are always fabricated using non-volatile liquids to measure pressure. Give one reason why volatile liquids would be inappropriate.
7. The pressure of a sample of gas is measured at sea level with a closed-end manometer. The liquid in the manometer is mercury. Determine the pressure of the gas in:
(a) Torr
(b) Pa
(c) bar

8. The pressure of a sample of gas is measured with an open-end manometer, partially shown to the right. The liquid in the manometer is mercury. Assuming atmospheric pressure is 1.010 atm, determine the pressure of the gas in:
(a) Torr
(b) Pa
(c) bar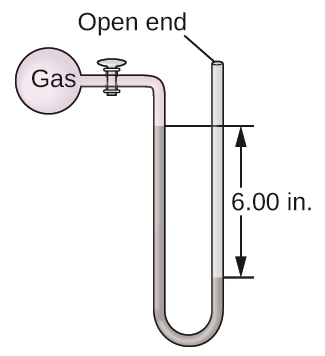
9. When you ride an elevator to the top floor of a skyscraper, you may notice the sensation of your ears “popping”. What physiological change are you experiencing?
Answers
1. (a) 197.4 atm
(b) 2.000 x 104 kPa
(c) 1.50 x 105 mmHg
4. 9075 N
5. By spreading out your weight over a larger surface area, you decrease the pressure applied to the ice, decreasing your risk of falling through the ice again.
6. If a volatile liquid was used, it would produce a vapour, which would exert its own partial pressure against the surface of the liquid, resulting in false measurements.
7. (a) 264 Torr
(b) 35 200 Pa
(c) 0.352 bar
8. (a) Pgas = 615.2 Torr
(b) P (in Pa) = 8.20 x 104 Pa
(c) P (in bar) = 0.820 bar
9. As you ascend in altitude, the atmospheric pressure outside your body decreases. Air trapped inside your body in your Eustachian tubes expands, building up pressure in your middle ear, until the tubes suddenly open. When they open, the pressure is equalized and your eardrums move, creating the “popping” sensation.
Force exerted per unit area
SI unit of pressure; 1 Pa = 1 N/m2
Unit of pressure; 1 bar = 100,000 Pa
Pressure that the air exerts on the surface of the Earth
Unit of pressure; 1 atm = 101,325 Pa = 760 mmHg
Device used to measure atmospheric pressure
Unit of pressure; another name for a millimetre of mercury; 1 Torr = 1760 atm
Device used to measure the pressure of a gas trapped in a container
Unit of temperature; water freezes at 32 °F and boils at 212 °F on this scale
Minimum possible temperature, labeled 0 K (zero kelvins); temperature at which the volume of a gas would be zero according to Charles’s law

