1.2 – Determining Chemical Formulae
Now that you’ve obtained a good understanding of the mole concept and its relation to masses and molar masses, we can now integrate this knowledge in this section. Here, we begin our discussion on expressing and understanding the chemical formulas for compounds and using these formulas to write out balanced chemical equations.
Chemical Formulas
A molecular formula is a representation of a molecule that uses chemical symbols to indicate the types of atoms followed by subscripts to show the number of atoms of each type in the molecule. (A subscript is used only when more than one atom of a given type is present.) Molecular formulas are also used as abbreviations for the names of compounds.
The structural formula for a compound gives the same information as its molecular formula (the types and numbers of atoms in the molecule) but also shows how the atoms are connected in the molecule. The structural formula for methane contains symbols for one C atom and four H atoms, indicating the number of atoms in the molecule (Figure 1.2.1). The use of lines in structural formulas represent covalent bonds that hold the atoms together (by the sharing of electrons between atoms) We will discuss chemical bonds and see how to predict the arrangement of atoms in a molecule later. For now, simply know that the lines are an indication of how the atoms are connected in a molecule. A ball-and-stick model shows the geometric arrangement of the atoms with atomic sizes not to scale, and a space-filling model shows the relative sizes of the atoms.
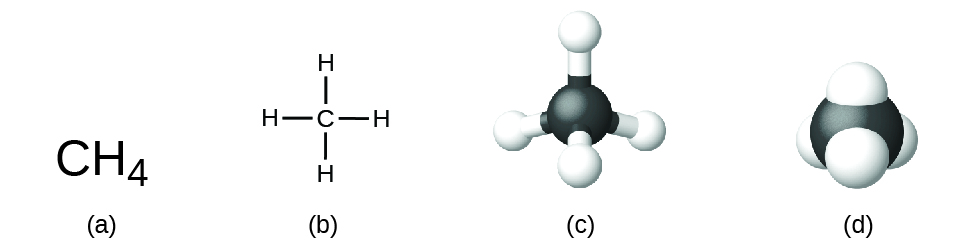
Figure 1.2.1. A methane molecule can be represented as (a) a molecular formula, (b) a structural formula, (c) a ball-and-stick model, and (d) a space-filling model. Carbon and hydrogen atoms are represented by black and white spheres, respectively.
Although many elements consist of discrete, individual atoms (e.g. carbon and the noble gases including helium, neon, and argon), some exist naturally as molecules made up of two or more atoms of the element chemically bonded together. For example, most samples of the elements hydrogen, oxygen, and nitrogen are composed of molecules that contain two atoms each (called diatomic molecules) and thus have the molecular formulas H2, O2, and N2, respectively. In other words, in their natural standard states, oxygen and nitrogen exist as diatomic molecules and very rarely as single oxygen or nitrogen atoms in their natural standard state. Other elements commonly found as diatomic molecules are fluorine (F2), chlorine (Cl2), bromine (Br2), and iodine (I2). The most common form of the element sulfur is composed of molecules that consist of eight atoms of sulfur; its molecular formula is S8 (Figure 1.2.2).

Figure 1.2.2. A molecule of sulfur is composed of eight sulfur atoms and is therefore written as S8. It can be represented as (a) a structural formula, (b) a ball-and-stick model, and (c) a space-filling model. Sulfur atoms are represented by yellow spheres.
It is extremely important to note as you move forward in chemistry that a subscript following a symbol and a number in front of a symbol do not represent the same thing. For example, H2 and 2H represent distinctly different species. H2 is a molecular formula; it represents a diatomic molecule of hydrogen, consisting of two atoms of the element that are covalently bonded together. The expression 2H, on the other hand, indicates two separate hydrogen atoms that are not combined as a unit. The expression 2H2 represents two molecules of diatomic hydrogen (Figure 1.2.3).
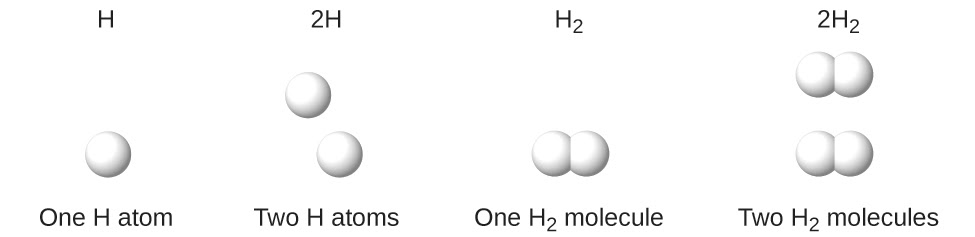
Figure 1.2.3. The symbols H, 2H, H2, and 2H2 represent very different entities.
It’s important to note that the empirical formula is not the same as the molecular formula (that was discussed at the beginning of this section); in a molecular formula, the subscripts indicate the actual numbers of atoms of each element in a single discrete molecule of the compound whereas the empirical formula only gives the simplest whole-number ratio of atoms/ions in the compound.
Empirical formulas are often a first step in determining a molecular formula. The following example highlights the difference between empirical formulas and molecular formulas. Recall that a molecule is made up of atoms covalently bonded together to form a single discrete unit. Consider the examples of ethyne, C2H2, and cyclobutadiene, C4H4, whose structural formulas are shown below in Figure 1.2.4. Notice that both of these molecules have the same ratio of carbon atoms to hydrogen atoms – atom-wise, they contain 50% carbon and 50% hydrogen. In other words, both compounds have the same empirical formula, CH, as this is the simplest whole number ratio of elements present. However, their molecular formulas are different multiples of this empirical formula: CH x 2 yields ethyne (C2H2) and CH x 4 yields cyclobutadiene (C4H4), two compounds with vastly different properties
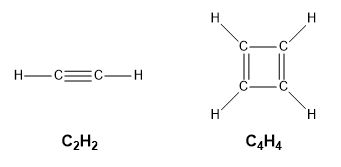
Figure 1.2.4. Structural formula for ethyne, C2H2, and cyclobutadiene, C4H4.
As we’ll discuss in greater detail in the final chapter on molecular bonding, ionic compounds form lattice structures that always have a whole-number multiple of repeating formula units. As long as we add whole number multiples of formula units of the same ionic compound, we could hypothetically have an infinitely large lattice structure. Hence, for the sake of simplicity, we use the empirical formula to describe the simplest ratio of ions. Table salt is denoted as NaCl since in any lattice structure of any size, whether you have 10 Na+ and 10 Cl– or 1000 Na+ and 1000 Cl–, there must always be one sodium cation (Na+) for each chloride anion (Cl–). Even if we write Na10Cl10, it will always be simplified to NaCl, and the identity of the compound remains the same.
In summary, the empirical formulas give you the ratio of different elements in a compound and molecular formulas give you the actual number of atoms in the molecule.
Let’s look at another example: the molecular formula for acetic acid, the component that gives vinegar its sharp taste, is C2H4O2. This formula indicates that a molecule of acetic acid (Figure 1.2.5) contains two carbon atoms, four hydrogen atoms, and two oxygen atoms. The ratio of atoms is 2:4:2. Dividing by the lowest common denominator (2) gives the simplest, whole-number ratio of atoms, 1:2:1, so the empirical formula is CH2O (but remember: this formula doesn’t denote the actual structure of the molecule – CH2O corresponds to formaldehyde, which is used for preserving biological specimens and even bodies of deceased persons!). Note that a molecular formula is always a whole-number multiple of an empirical formula.
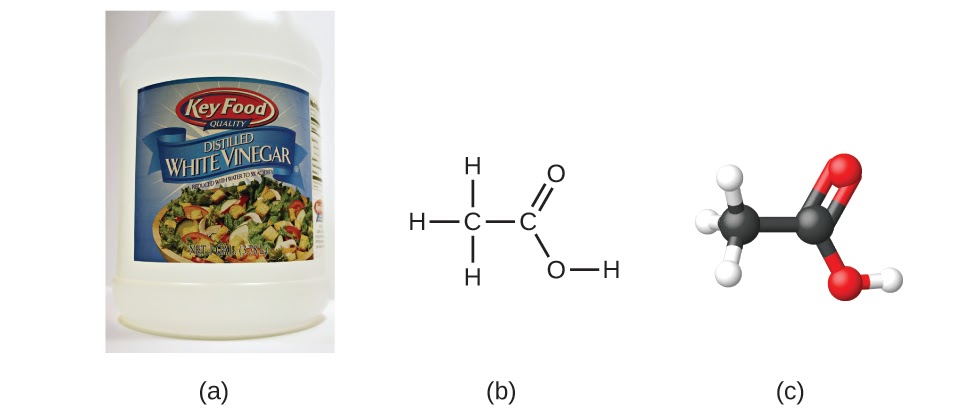
Figure 1.2.5. (a) Vinegar contains acetic acid, C2H4O2, which has an empirical formula of CH2O. It can be represented as (b) a structural formula and (c) as a ball-and-stick model. (credit a: modification of work by “HomeSpot HQ”/Flickr)
Determination of Empirical Formulas
The most common approach to determining a compound’s chemical formula is to first measure the masses of its constituent elements. However, we must keep in mind that chemical formulas represent the relative numbers, not masses, of atoms in the substance. Therefore, any experimentally derived data involving mass must be used to derive the corresponding numbers of atoms in the compound. To accomplish this, we can use molar masses to convert the mass of each element to a number of moles. We then consider the moles of each element relative to each other, converting these numbers into a whole-number ratio that can be used to derive the empirical formula of the substance.
Consider a sample of a compound determined to contain 1.71 g C and 0.287 g H. The corresponding numbers of atoms (in moles) are:
![]()
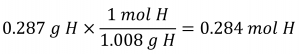
Thus, we can accurately represent this compound with the formula C0.142H0.248. Of course, per accepted convention, formulas contain whole-number subscripts, which can be achieved by dividing each subscript by the smaller subscript:
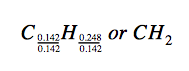
(Recall that subscripts of “1” are not written but rather assumed if no other number is present.)
The empirical formula for this compound is thus CH2. This may or not be the compound’s molecular formula as well; however, we would need additional information to make that determination (as discussed later in this section).
Consider as another example a sample of a compound determined to contain 5.31 g Cl and 8.40 g O. Following the same approach yields a tentative empirical formula of:
![]()
As shown in this case, occasionally when performing this calculation a fractional value (instead of a whole number) is obtained. Since it is impossible to have a fractions of an atom, the value must correspondingly be multiplied by an appropriate factor in order to get a whole integer, as shown in the following examples:
In summary, empirical formulas are derived from experimentally measured element masses by:
1. Deriving the number of moles of each element from its mass
2. Dividing each element’s molar amount by the smallest molar amount to yield subscripts for a tentative empirical formula
3. Multiplying all coefficients by an integer, if necessary, to ensure that the smallest whole-number ratio of subscripts is obtained
Figure 1.2.6 outlines this procedure in flow-chart fashion for a substance containing elements A and X.
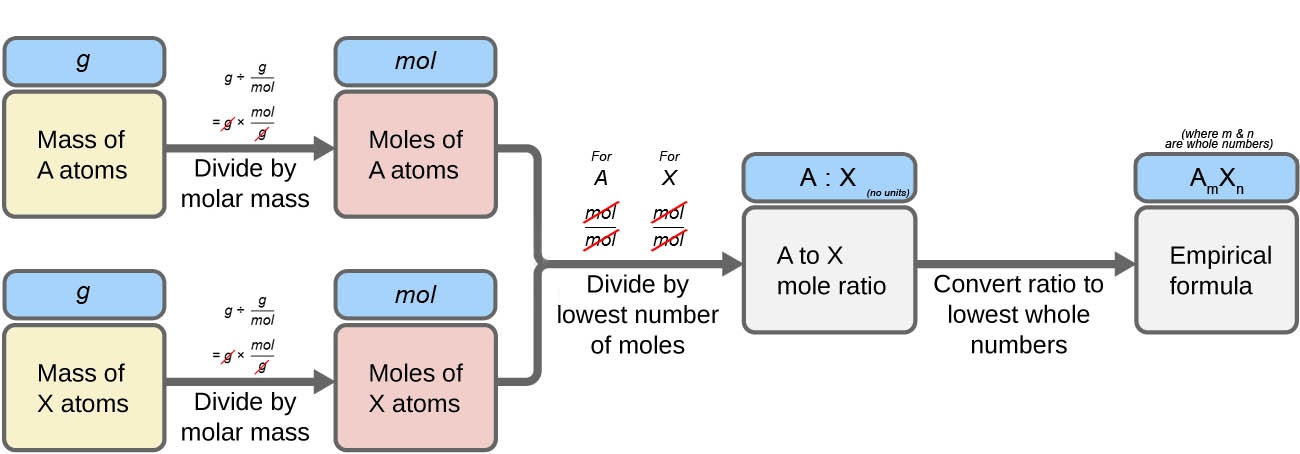
Figure 1.2.6. The empirical formula of a compound can be derived from the masses of all elements in the sample.
Example 1.2.1 – Determining a Compound’s Empirical Formula from the Masses of
Its Elements
A sample of the black mineral hematite (Figure 1.2.7), an oxide of iron found in many iron ores, contains 34.97 g of iron and 15.03 g of oxygen. What is the empirical formula of hematite?

Figure 1.2.7. Hematite is an iron oxide that is used in jewelry. (credit: Mauro Cateb)
Solution
For this problem, we are given the mass in grams of each element. Begin by finding the moles of each:
![]()
![]()
Next, derive the iron-to-oxygen molar ratio by dividing by the lesser
number of moles:
![]()
![]()
The ratio is 1.000 mol of iron to 1.500 mol of oxygen (Fe1O1.5). Finally, multiply the ratio by two to get the smallest possible whole number subscripts while still maintaining the correct iron-to-oxygen ratio:
2(Fe1O1.5) = Fe2O3
The empirical formula is Fe2O3.
Check Your Learning 1.2.1 – Determining a Compound’s Empirical Formula from
the Masses of Its Elements
What is the empirical formula of a compound if a sample contains 0.130 g of nitrogen and 0.370 g of oxygen?
Answer
N2O5
Deriving Empirical Formulas from Percent Composition
With regard to deriving empirical formulas, consider instances in which a compound’s percent composition is available rather than the absolute masses of the compound’s constituent elements. In such cases, the percent composition can be used to calculate the masses of elements present in any convenient mass of compound; these masses can then be used to derive the empirical formula in the usual fashion.
Example 1.2.2 – Determining an Empirical Formula from Percent Composition
The bacterial fermentation of grain to produce ethanol forms a gas with a percent composition of 27.29 % C and 72.71% O (Figure 1.2.8). What is the empirical formula for this gas?

Figure 1.2.8. An oxide of carbon is removed from these fermentation tanks through the large copper pipes at the top. (credit: “Dual Freq”/Wikimedia Commons)
Solution
Since the scale for percentages is 100, it is most convenient to calculate the mass of elements present in a sample weighing 100 g. The calculation is “most convenient” because, per the definition for percent composition, the mass of a given element in grams is numerically equivalent to the element’s mass percentage. This numerical equivalence results from the definition of the “percentage” unit, whose name is derived from the Latin phrase per centum meaning “by the hundred.” Considering this definition, the mass percentages provided may be more conveniently expressed as fractions: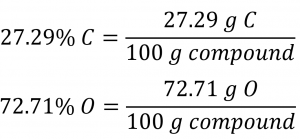
The molar amounts of carbon and hydrogen in a 100 g sample are calculated by dividing each element’s mass by its molar mass: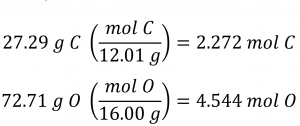
Coefficients for the tentative empirical formula are derived by dividing each molar amount by the lesser of the two: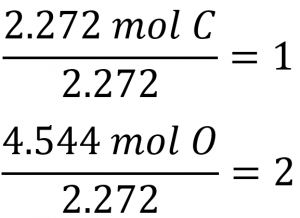
Since the resulting ratio is one carbon to two oxygen atoms, the empirical formula is CO2.
Check Your Learning 1.2.2 – Determining an Empirical Formula from Percent
Composition
What is the empirical formula of a compound containing 40.0 % C, 6.71 % H, and 53.28 % O?
Answer
CH2O
Deriving Empirical Formulas from Combustion Analysis
The elemental composition of hydrocarbons (organic compounds consisting entirely of carbon and hydrogen atoms) and related compounds containing C, H and other elements may be determined via combustion analysis. In combustion analysis, a weighed sample of the compound is heated to a high temperature under a stream of oxygen gas (O2), resulting in its complete combustion to yield gaseous products of known identities. The complete combustion of hydrocarbons, for example, will yield carbon dioxide and water as the only products. The gaseous combustion products are swept through separate, preweighed collection devices containing compounds that selectively absorb each product (Figure 1.2.9). The mass increase of each device corresponds to the mass of the absorbed product and may be used in an appropriate stoichiometric calculation to derive the mass of the relevant element.
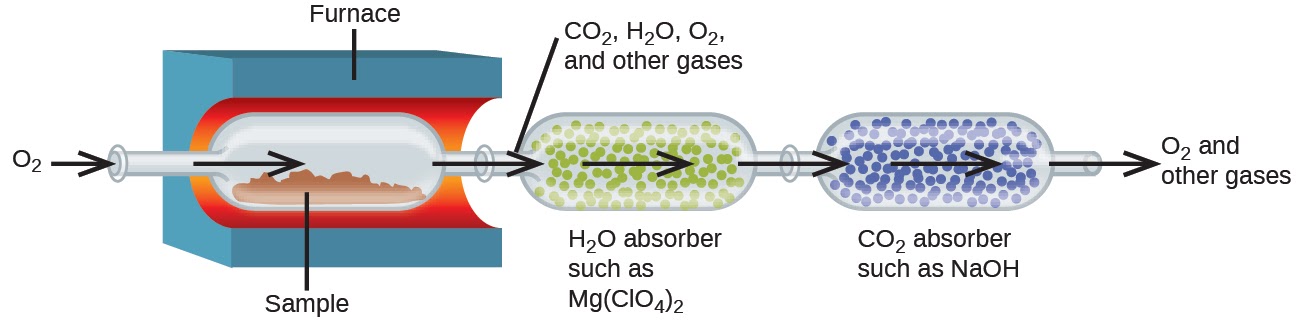
Figure 1.2.9. This schematic diagram illustrates the basic components of a combustion analysis device for determining the carbon and hydrogen content of a sample.
|
Combustion Analysis Problems – Underlying Assumption |
|
You’ll frequently come across combustion analysis problems as you practice determining empirical (and later on molecular) formulas from data obtained on the collection of combustion products. For all combustion analysis problems you come across, always keep in the back of your mind the following underlying assumption – the combustion reaction is complete. In other words, assume that there are no other side-products produced in the combustion reaction; only the product compounds mentioned in the problem are formed. Therefore, for hydrocarbons and compounds containing C, H, and O, this means that only gaseous carbon dioxide and water are produced. For other compounds containing other elements such as S and N, you can expect to see other oxidation compounds form as well, including SO2 and NO2; these will be mentioned in the question to help you determine the identity of the unknown compound. If it were an incomplete combustion, side-products such as carbon monoxide, carbon (soot), and nitric oxide (NO) would form, making it extremely difficult, if not impossible, to determine the composition of elements and identity of your sample. For this reason, the combustion process uses an excess of oxygen gas, in order to ensure as complete a combustion as possible. As a consequence, if the sample undergoing analysis contains oxygen, this component will need to be found by difference (all other elements must be determined first, and then any remaining sample mass is assumed to be due to oxygen). An example of this type of deduction is shown in Example 1.2.4. |
Example 1.2.3 – Combustion Analysis
Polyethylene is a hydrocarbon polymer used to produce food-storage bags and many other flexible plastic items. Combustion analysis of a 0.00126 g sample of polyethylene yields 0.00394 g of CO2 and 0.00161 g of H2O. What is the empirical formula of polyethylene?
Solution
The primary assumption in this exercise is that all the carbon in the sample combusted is converted to carbon dioxide (CO2), and all the hydrogen in the sample is converted to water, H2O (note that the sample, being a hydrocarbon, is represented by CxHy):
CxHy (s) + excess O2 (g) ⟶ x CO2 (g) + y 2H2O (g)
Note that a balanced equation is not necessary for the task at hand. To derive the empirical formula of the compound, only the subscripts x and y are needed.
First, calculate the molar amounts of carbon and hydrogen in the sample, using the provided masses of the carbon dioxide and water, respectively. As shown in the calculation below, note that each mole of water formed requires 2 moles of H atoms.
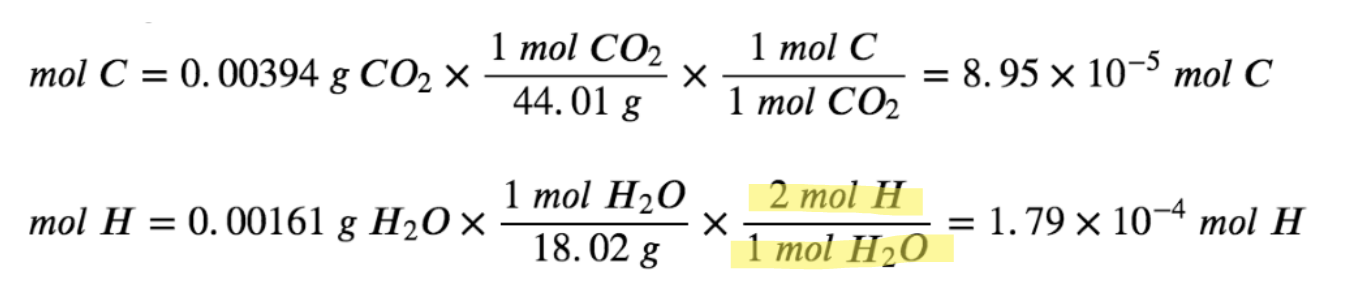
The empirical formula for the compound is then derived by identifying the smallest whole-number multiples for these molar amounts. The H-to-C molar ratio is:
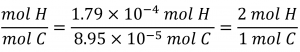
The empirical formula for polyethylene is CH2. Again, note that this is the empirical formula, not the molecular formula of this substance
Check Your Learning 1.2.3 – Combustion Analysis
A 0.00215 g sample of polystyrene, a polymer composed of carbon and hydrogen, produced 0.00726 g of CO2 and 0.00148 g of H2O by combustion analysis. What is the empirical formula for polystyrene?
Answer
CH
Example 1.2.4 – Combustion Analysis
Salicylic acid is used to make aspirin. It contains only carbon, oxygen, and hydrogen. Combustion of a 43.5 mg sample of this compound produced 97.1 mg of CO2 and 17.0 mg of H2O. What is the empirical formula of salicylic acid?
Answer
The primary assumption in this exercise is that all the carbon in the sample combusted is converted to carbon dioxide (CO2), all the hydrogen in the sample is converted to water (H2O), and all of the oxygen is converted to either carbon dioxide or water.
First, calculate the molar amounts of carbon and hydrogen in the sample, using the provided masses of the carbon dioxide and water, respectively:
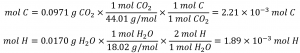
Knowing the molar masses of carbon and hydrogen, we can convert these molar values into masses; consequently, these will represent the mass of carbon and hydrogen in the sample:
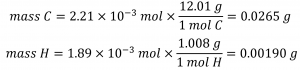
If we know the mass of the sample and the mass of carbon and hydrogen individually in the sample, the remaining mass must be oxygen, for which we find its molar amount:
mO = msample– mC – mH
mO = 0.0435 g – 0.0265 g – 0.00190 g
mO = 0.0151 g
![]()
The empirical formula for the compound is then derived by identifying the smallest whole-number multiples for these molar amounts. The C-to-O and H-to-O molar ratio is
C2.33H2.00O1.00 x3
= C(2.33)(3)H(2.00)(3)O(1.00)(3)
= C7H6O3
Hence, the empirical formula for salicylic acid is C7H6O3.
Check Your Learning 1.2.5 – Combustion Analysis
A 2.0714 g sample containing carbon, hydrogen, and oxygen was burned in a combustion analysis apparatus; 1.928 g of H2O and 4.709 g of CO2 were produced. Separately, the molar mass of the sample was found to be 116.16 g/mol. Determine the empirical formula of the sample.
Answer
Empirical formula: C3H6O
Determination of Molecular Formulas
Recall that empirical formulas are symbols representing the relative numbers of a compound’s elements. Determining the absolute numbers of atoms that compose a single molecule of a covalent compound requires knowledge of both its empirical formula and its molecular mass or molar mass. These quantities may be determined experimentally by various measurement techniques. Molecular mass, for example, is often derived from the mass spectrum of the compound (see discussion of this technique in the box below). Molar mass can be measured by a number of experimental methods, many of which will be introduced in later chapters of this text.
|
In Case You’re Interested…Mass Spectrometry |
|
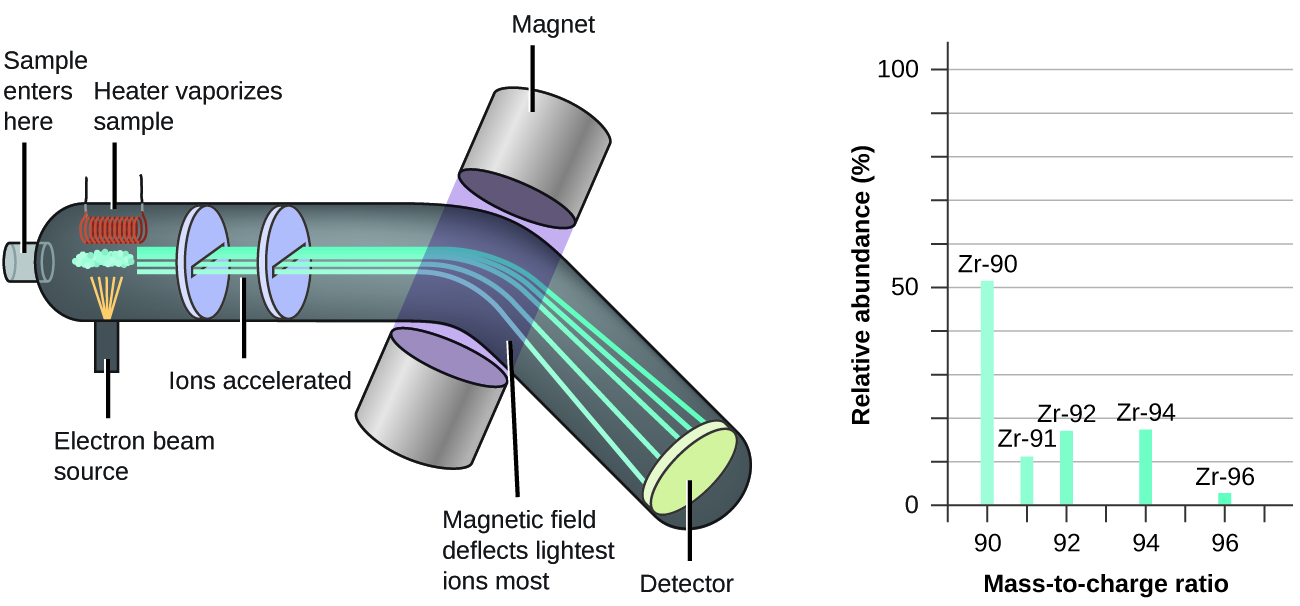
Mass spectrometry (MS) is widely used in chemistry, forensics, medicine, environmental science, and many other fields to analyze and help identify the substances in a sample of material. In a typical mass spectrometer (Figure 1.2.10):
Figure 1.2.10. Analysis of zirconium in a mass spectrometer produces a mass spectrum with peaks showing the different isotopes of Zr. Since its initial use during the development of modern atomic theory, MS has evolved to become a powerful tool for chemical analysis in a wide range of applications. For more information you can check out the following videos (podcast video #1; educational video #2 from the Royal Society of Chemistry) that explain and animate the process of mass spectrometry. |
Molecular formulas are derived by comparing the compound’s molecular or molar mass to its empirical formula mass. As the name suggests, an empirical formula mass is the sum of the average atomic masses of all the atoms represented in an empirical formula. If we know the molecular (or molar) mass of the substance, we can divide this by the empirical formula mass in order to identify the number of empirical formula units per molecule, which we designate as n:
![]()
The molecular formula is then obtained by multiplying each subscript in the empirical formula by n, as shown by the generic empirical formula AxBy:
(AxBy)n=AnxBny
Since the molecular formula is proportional to the empirical formula, their molecular masses will this also be proportional:
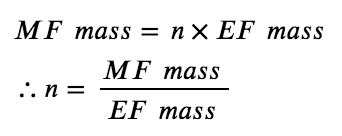
For example, consider a covalent compound whose empirical formula is determined to be CH2O. The empirical formula mass for this compound is approximately 30 amu (the sum of 12 amu for one C atom, 2 amu for two H atoms, and 16 amu for one O atom). If the compound’s molecular mass is determined to be 180 amu, this indicates that molecules of this compound contain six times the number of atoms represented in the empirical formula:

Molecules of this compound are then represented by molecular formulas whose subscripts are six times greater than those in the empirical formula:
MF= n x EF
= 6 x CH2O
= C6H12O6
Note that this same approach may be used when the molar mass (g/mol) instead of the molecular mass (amu) is used. In this case, we are merely considering one mole of empirical formula units and molecules, as opposed to single units and molecules.
Example 1.2.4 – Determination of Molecular Formulas
Nicotine (Figure 1.2.11), an alkaloid in the nightshade family of plants that is mainly responsible for the addictive nature of cigarettes, contains 74.02 % C, 8.710 % H, and 17.27 % N. If 40.57 g of nicotine contains 0.2500 mol nicotine, what is the molecular formula?
.

Figure 1.2.11. 2D and 3D structure of nicotine
Solution
Determining the molecular formula from the provided data will require a comparison of the compound’s empirical formula mass to its molar mass. As the first step, use the percent composition to derive the compound’s empirical formula. Assuming a convenient, 100 g sample of nicotine yields the following molar amounts of its elements:
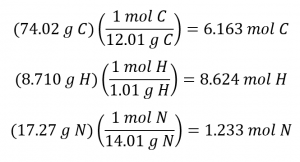
Next, we calculate the molar ratios of these elements relative to the least abundant element, N.
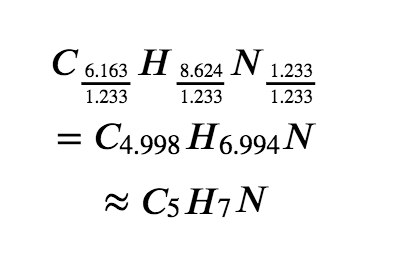
The C-to-N and H-to-N molar ratios are adequately close to whole numbers, and so the empirical formula is C5H7N. The empirical formula mass for this compound is therefore 81.13 amu, or 81.13 g/mol (as a molar empirical formula mass).
We calculate the molar mass for nicotine from the given mass and molar amount of compound:

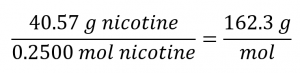
Comparing the molar mass and empirical formula mass indicates that each nicotine molecule contains two formula units:
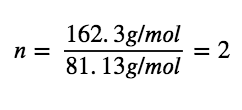
Thus, we can derive the molecular formula for nicotine from the empirical formula by multiplying each subscript by two:
MF= n x EF
= 2 x C5H7N
= C10H14N2
Check Your Learning 1.2.6 – Determination of Molecular Formulas
A major textile dye manufacturer developed a new yellow dye. The dye has a percent composition of 75.95% C, 17.72% N, and 6.33% H by mass with a molar mass of about 240 g/mol. Determine the molecular formula of the dye.
Answer
C15H15N3
It is important to be aware that it may be possible for the same atoms to be arranged in different ways. Compounds with the same molecular formula may have different atom-to-atom bonding and, therefore different structures and properties, these are known as isomers. You’ll learn much more about different types of isomers in CHM 1321 (Organic Chemistry I).
Writing and Balancing Chemical Equations
When atoms gain or lose electrons to yield ions or combine with other atoms to form molecules, their symbols are modified or combined to generate chemical formulas (as we’ve seen so far in this section) that appropriately represent these species. Extending this symbolism to represent both the identities and the relative quantities of substances undergoing a chemical (or physical) change/reaction involves writing and balancing a chemical equation. Consider as an example the reaction between one methane molecule (CH4) and two diatomic oxygen molecules (O2) to produce one carbon dioxide molecule (CO2) and two water molecules (H2O). The chemical equation representing this process is provided in the upper half of Figure 1.2.12, with space-filling molecular models shown in the lower half of the figure.
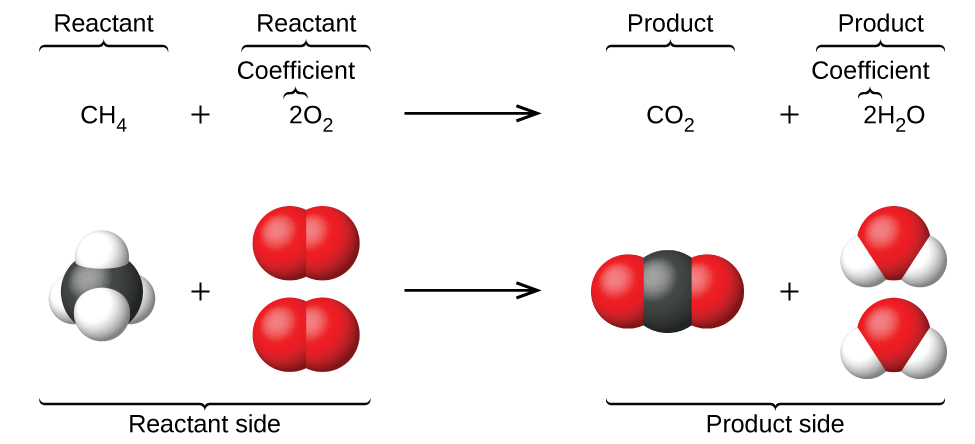
Figure 1.2.12. The reaction between methane and oxygen to yield carbon dioxide and water (shown at bottom) may be represented by a chemical equation using formulas (top).
This example illustrates the fundamental aspects of any chemical equation:
1. The substances undergoing reaction are called reactants, and their formulas are placed on the left side of the equation.
2. The substances generated by the reaction are called products, and their formulas are placed on the right side of the equation.
3. Plus signs (+) separate individual reactant and product formulas, and an arrow (⟶) separates the reactant and product (left and right) sides of the equation.
4. The relative numbers of reactant and product species are represented by coefficients (numbers placed immediately to the left of each formula). A coefficient of 1 is typically omitted.
It is common practice to use the smallest possible whole-number coefficients in a chemical equation, as is done in this example. Realize, however, that these coefficients represent the relative numbers of reactants and products, and, therefore, they may be correctly interpreted as ratios. Methane and oxygen react to yield carbon dioxide and water in a 1:2:1:2 ratio. This ratio is satisfied if the numbers of these molecules are, respectively, 1-2-1-2, or 2-4-2-4, or 3-6-3-6, and so on (Figure 1.2.13). Likewise, these coefficients may be interpreted with regard to any amount (number) unit, and so this equation may be correctly read in many ways, including:
One methane molecule and two oxygen molecules react to yield one carbon dioxide molecule and two water molecules.
One dozen methane molecules and two dozen oxygen molecules react to yield one dozen carbon dioxide molecules and two dozen water molecules.
One mole of methane molecules and 2 moles of oxygen molecules react to yield 1 mole of carbon dioxide molecules and 2 moles of water molecules.
 Figure 1.2.13. Regardless of the absolute numbers of molecules involved, the ratios between numbers of molecules of each species that react (the reactants) and molecules of each species that form (the products) are the same and are given by the chemical reaction equation.
Figure 1.2.13. Regardless of the absolute numbers of molecules involved, the ratios between numbers of molecules of each species that react (the reactants) and molecules of each species that form (the products) are the same and are given by the chemical reaction equation.
Balancing Equations
The chemical equation is called balanced when an equal numbers of atoms for each element involved in the reaction are represented on the reactant and product sides. This is a requirement the equation must satisfy to be consistent with the law of conservation of matter. It may be confirmed by simply summing the numbers of atoms on either side of the arrow and comparing these sums to ensure they are equal. Note that the number of atoms for a given element is calculated by multiplying the coefficient of any formula containing that element by the element’s subscript in the formula. If an element appears in more than one formula on a given side of the equation, the number of atoms represented in each must be computed and then added together. For example, both product species in the example reaction of Figure 1.2.12, CO2 and H2O, contain the element oxygen, and so the number of oxygen atoms on the product side of the equation is:
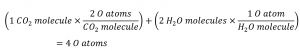
The equation for the reaction between methane and oxygen to yield carbon dioxide and water is confirmed to be balanced per this approach, as shown here:
CH4 + 2O2 ⟶ CO2 + 2H2O
|
Element |
Reactants |
Products |
Balanced? |
|
C |
1 x 1 = 1 |
1 x 1 = 1 |
1 = 1, yes |
|
H |
4 x 1 = 4 |
2 x 2 = 4 |
4 = 4, yes |
|
O |
2 x 2 = 4 |
(1 x 2) + (2 x 1) = 4 |
4 = 4, yes |
A balanced chemical equation often may be derived from a qualitative description of some chemical reaction by a fairly simple approach known as balancing by inspection. Consider as an example, the decomposition of water to yield molecular hydrogen and oxygen. This process is represented qualitatively by an unbalanced chemical equation:
H2O → H2 + O2 (unbalanced)
Comparing the number of H and O atoms on either side of this equation confirms its imbalance:
|
Element |
Reactants |
Products |
Balanced? |
|
H |
1 x 2 = 2 |
1 x 2 = 2 |
2 = 2, yes |
|
O |
1 x 1 = 1 |
1 x 2 = 2 |
1 ≠ 2, no |
The numbers of H atoms on the reactant and product sides of the equation are equal, but the numbers of O atoms are not. To achieve balance, the coefficients of the equation may be changed as needed. Keep in mind, of course, that the formula subscripts define, in part, the identity of the substance, and so these cannot be changed without altering the qualitative meaning of the equation. For example, changing the reactant formula from H2O to H2O2 would yield balance in the number of atoms, but doing so also changes the reactant’s identity (it’s now hydrogen peroxide and not water). The O atom balance may be achieved by changing the coefficient for H2O to 2.
2H2O → H2 + O2 (unbalanced)
|
Element |
Reactants |
Products |
Balanced? |
|
H |
2 x 2 = 4 |
1 x 2 = 2 |
4 ≠ 2, no |
|
O |
2 x 1 = 2 |
1 x 2 = 2 |
2 = 2, yes |
The H atom balance was upset by this change, but it is easily reestablished by changing the coefficient for the H2 product to 2.
2H2O → 2H2 + O2 (balanced)
|
Element |
Reactants |
Products |
Balanced? |
|
H |
2 x 2 = 4 |
2 x 2 = 4 |
4 = 4, yes |
|
O |
2 x 1 = 2 |
1 x 2 = 2 |
2 = 2, yes |
2H2O → 2H2 + O2
Example 1.2.5 – Balancing Equations
Write a balanced equation for the reaction of molecular nitrogen (N2) and oxygen (O2) to form dinitrogen pentoxide.
Solution
First, write the unbalanced equation.
N2 + O2 → N2O5 (unbalanced)
Next, count the number of each type of atom present in the unbalanced
equation.
|
Element |
Reactants |
Products |
Balanced? |
|
N |
1 x 2 = 2 |
1 x 2 = 2 |
2 = 2, yes |
|
O |
1 x 2 = 2 |
1 x 5 = 5 |
2 ≠ 5, no |
N2 + 5O2 → 2N2O5 (unbalanced)
|
Element |
Reactants |
Products |
Balanced? |
|
N |
1 x 2 = 2 |
2 x 2 = 4 |
2 ≠ 4, no |
|
O |
5 x 2 = 10 |
2 x 5 = 10 |
10 = 10, yes |
2N2 + 5O2 → 2N2O5 (balanced)
|
Element |
Reactants |
Products |
Balanced? |
|
N |
2 x 2 = 4 |
2 x 2 = 4 |
4 = 4, yes |
|
O |
5 x 2 = 10 |
2 x 5 = 10 |
10 = 10, yes |
The numbers of N and O atoms on either side of the equation are now equal, and so the equation is balanced.
Check Your Learning 1.2.7 – Balancing Equations
Write a balanced equation for the decomposition of ammonium nitrate to form molecular nitrogen, molecular oxygen, and water. (Hint: Balance oxygen last, since it is present in more than one molecule on the right side of the equation.)
Answer
2NH4NO3 ⟶ 2N2 + O2 + 4H2O
It is sometimes convenient to use fractions instead of integers as intermediate coefficients in the process of balancing a chemical equation. When balance is achieved, all the equation’s coefficients may then be multiplied by a whole number to convert the fractional coefficients to integers without upsetting the atom balance. For example, consider the reaction of ethane (C2H6) with oxygen to yield H2O and CO2, represented by the unbalanced equation:
C2H6 + O2 → H2O + CO2 (unbalanced)
Following the usual inspection approach, one might first balance C and H atoms by changing the coefficients for the two product species, as shown:
C2H6 + O2 → 3H2O + 2CO2 (unbalanced)
This results in seven O atoms on the product side of the equation, an odd number—no integer coefficient can be used with the O2 reactant to yield an odd number, so a fractional coefficient, 7/2, is used instead to yield a provisional balanced equation: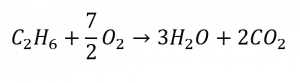
A conventional balanced equation with integer-only coefficients is derived by multiplying each coefficient by 2:
2C2H6 + 7O2 → 6H2O + 4CO2
Finally with regard to balanced equations, recall that convention dictates the use of the smallest whole-number coefficients. Although the equation for the reaction between molecular nitrogen and molecular hydrogen to produce ammonia is indeed balanced:
3N2 + 9H2 → 6NH3
the coefficients are not the smallest possible integers representing the relative numbers of reactant and product molecules. Dividing each coefficient by the greatest common factor, 3, gives the preferred equation:
N2 + 3H2 → 2NH3
|
Balancing Chemical Equations – Additional Practice |
|
Balancing chemical equations is an extremely important and fundamental skill you’ll need to master to succeed in general chemistry and many other chemistry-related courses. |
Additional Information in Chemical Equations
The physical states of reactants and products in chemical equations very often are indicated with a parenthetical abbreviation following the formulas. Common abbreviations include s for solids, l for liquids, g for gases, and aq for substances dissolved in water (aqueous solutions). These notations are illustrated in the example equation here:
Na (s) + 2H2O (l) → 2NaOH (aq) + H2 (g)
This equation represents the reaction that takes place when sodium metal is placed in water. The solid sodium reacts with liquid water to produce molecular hydrogen gas and the ionic compound sodium hydroxide (a solid in pure form, but readily dissolved in water).
Special conditions necessary for a reaction are sometimes designated by writing a word or symbol above or below the equation’s arrow. For example, a reaction carried out by heating may be indicated by the uppercase Greek letter delta (Δ) over the arrow.
Other examples of these special conditions will be encountered in more depth in later chapters.
★ Questions
1. Write the molecular and empirical formulas of the following compounds
(a)
(b)
(c)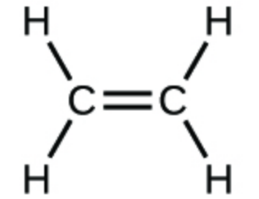
(d)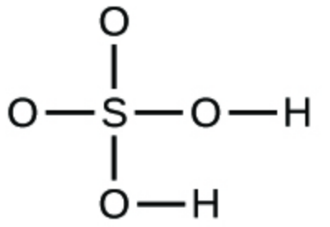
2. Open the Build a Molecule simulation and select the “Larger Molecules” tab. Select an appropriate atoms “Kit” to build a molecule with two carbon and six hydrogen atoms. Drag atoms into the space above the “Kit” to make a molecule. A name will appear when you have made an actual molecule that exists (even if it is not the one you want). You can use the scissors tool to separate atoms if you would like to change the connections. Click on “3D” to see the molecule, and look at both the space-filling and ball-and-stick possibilities.
(a) Draw the structural formula of this molecule and state its name.
(b) Can you arrange these atoms in any way to make a different compound? If so, draw its structural formula and state its name.
(c) How are the molecules drawn in (a) and (b) the same? How do they differ? What are they called (the type of relationship between these molecules, not their names).
3. Calculate the following to four significant figures:
(a) the percent composition of ammonia, NH3.
(b) the percent composition of photographic “hypo,” Na2S2O3.
(c) the percent of calcium ion in Ca3(PO4)2.
★★ Questions
4. Determine the empirical formulas for compounds with the following percent compositions:
(a) 43.6 % phosphorus and 56.4 % oxygen
(b) 28.7 % K, 1.5 % H, 22.8 % P, and 47.0 % O
5. Dichloroethane, a compound that is often used for dry cleaning, contains carbon, hydrogen, and chlorine. It has a molar mass of 99 g/mol. Analysis of a sample shows that it contains 24.3 % carbon and 4.1 % hydrogen. What is its molecular formula?
6. A major textile dye manufacturer developed a new yellow dye. The dye has a percent composition of 75.95 % C, 17.72 % N, and 6.33 % H by mass with a molar mass of about 240 g/mol. Determine the molecular formula of the dye.
7. How many moles of CO2 and H2O will be produced by combustion analysis of 0.010 mol of styrene?
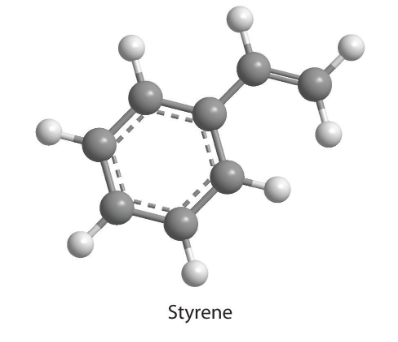
8. Combustion of a 34.8 mg sample of benzaldehyde, which contains only carbon, hydrogen, and oxygen, produced 101 mg of CO2 and 17.7 mg of H2O.
(a) What was the mass of carbon and hydrogen in the sample?
(b) Assuming that the original sample contained only carbon, hydrogen, and oxygen, what was the mass of oxygen in the sample?
(c) What was the mass percentage of oxygen in the sample?
(d) What is the empirical formula of benzaldehyde?
(e) The molar mass of benzaldehyde is 106.12 g/mol. What is its molecular formula?
★ Questions (Part 2)
9. Balance the following equations:
(a) PCl5 (s) + H2O (l) → POCl3 (l) + HCl (aq)
(b) Cu (s) + HNO3 (aq) → Cu(NO3)2 (aq) + H2O (l) + NO (g)
(c) H2 (g) + I2 (s) → HI (s)
(d) Fe (s) + O2 (g) → Fe2O3 (s)
(e) Na (s) + H2O (l) → NaOH (aq) + H2 (g)
(f) (NH4)2Cr2O7 (s) → Cr2O3 (s) + N2 (g) +H2O (g)
(g) P4 (s) + Cl2 (g) → PCl3 (l)
(h) PtCl4 (s) → Pt (s) + Cl2 (g)
10. Write a balanced molecular equation describing each of the following chemical reactions.
(a) Solid calcium carbonate is heated and decomposes to solid calcium oxide and carbon dioxide gas.
(b) Gaseous butane, C4H10, reacts with diatomic oxygen gas to yield gaseous carbon dioxide and water vapour.
(c) Aqueous solutions of magnesium chloride and sodium hydroxide react to produce solid magnesium hydroxide and aqueous sodium chloride.
(d) Water vapor reacts with sodium metal to produce solid sodium hydroxide and hydrogen gas.
★★ Questions (Part 2)
11. A novel process for obtaining magnesium from sea water involves several reactions. Write a balanced chemical equation for each step of the process.
(a) The first step is the decomposition of solid calcium carbonate from seashells to form solid calcium oxide and gaseous carbon dioxide.
(b) The second step is the formation of solid calcium hydroxide as the only product from the reaction of the solid calcium oxide with liquid water.
(c) Solid calcium hydroxide is then added to the seawater, reacting with dissolved magnesium chloride to yield solid magnesium hydroxide and aqueous calcium chloride.
(d) The solid magnesium hydroxide is added to a hydrochloric acid solution, producing dissolved magnesium chloride and liquid water.
(e) Finally, the magnesium chloride is melted and electrolyzed to yield liquid magnesium metal and diatomic chlorine gas.
Answers
1. (a) molecular CO2, empirical CO2; (b) molecular C2H2, empirical CH; (c) molecular C2H4, empirical CH2; (d) molecular H2SO4, empirical H2SO4
2. (a) Ethane
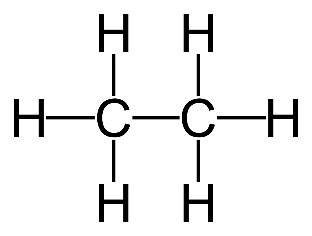
(b) There are no other ways to arrange the atoms.
(c) n/a
3. (a) 17.8% H, 82.2% N; (b) 29.1% Na, 30.4% O, 40.6% S; (c) 38.8% Ca, 41.3% O, 20.0% P
4. (a) P2O5 (b) KH2PO4
5. C2H4Cl2
6. C15H15N3
7. Moles of CO2: 0.08 mol CO2, moles of H2O: 0.04 mol H2O
8. (a) 27.6 mg C and 1.98 mg H; (b) 5.2 mg O; (c) 15%; (d) C7H6O; (e) C7H6O
9. (a) PCl5 (s) + H2O (l) → POCl3 (l) + 2 HCl (aq)
(b) 3 Cu (s) + 8 HNO3 (aq) → 3 Cu(NO3)2 (aq) + 4 H2O (l) + 2 NO (g)
(c) H2 (g) + I2 (s) → 2 HI (s)
(d) 4 Fe (s) + 3 O2 (g) → 2 Fe2O3 (s)
(e) 2 Na (s) + 2 H2O (l) → 2 NaOH (aq) + H2 (g)
(f) (NH4)2Cr2O7 (s) → Cr2O3 (s) + N2 (g) + 4 H2O (g)
(g) P4 (s) + 6 Cl2 (g) → 4 PCl3 (l)
(h) PtCl4 (s) → Pt (s) + 2 Cl2 (g)
10. (a) CaCO3 (s) → CaO (s) + CO2 (g)
(b) 2 C4H10 (g) + 13 O2 (g) → 8 CO2 (g) + 10 H2O (g)
(c) MgCl2 (aq) + 2 NaOH (aq) → Mg(OH)2 (s) + 2 NaCl (aq)
(d) 2 H2O (g) + 2 Na (s) → 2 NaOH (s) + H2 (g)
11. (a) CaCO3 (s) → CaO (s) + CO2 (g)
(b) CaO (s) + H2O (l) → Ca(OH)2 (s)
(c) Ca(OH)2 (s) + MgCl2 (aq) → Mg(OH)2 (s) + CaCl2 (aq)
(d) Mg(OH)2 (s) + 2HCl (aq) → MgCl2 (aq) + 2H2O (l)
(e) MgCl2 (l ) → Mg (l) + Cl2 (g)
Formula indicating the composition of a molecule of a compound and giving the actual number of atoms of each element in a molecule of the compound.
Shows the atoms in a molecule and how they are connected
Formula showing the composition of a compound given as the simplest whole-number ratio of atoms
Gravimetric technique used to determine the elemental composition of a compound via the collection and weighing of its gaseous combustion products
Sum of average atomic masses for all atoms represented in an empirical formula
Concise way, using symbols or formulas, of representing a chemical reaction
Substance undergoing a chemical or physical change; shown on the left side of the arrow in a chemical equation
A substance formed by a chemical or physical change; shown on the right side of the arrow in a chemical equation
Chemical equation with equal numbers of atoms for each element in the reactant and product