7.6 – Transition State Theory

Transition state theory (TST) provides a more accurate alternative to the previously used Arrhenius equation and the collision theory. The transition state theory attempts to provide a greater understanding of activation energy, E_a, and the thermodynamic properties involving the transition state. Collision theory of reaction rate, although intuitive, lacks an accurate method to predict the probability factor for the reaction. The theory assumes that reactants are hard spheres rather than molecules with specific structures. In 1935, Henry Eyring helped develop a new theory called the transition state theory to provide a more accurate alternative to the previously used Arrhenius equation and the collision theory. The Eyring equation involves the statistical frequency factory, v, which is fundamental to the theory.

According to TST, between the state where molecules are reactants and the state where molecules are products, there is the transition state. In the transition state, the reactants are combined in a species called the activated complex. The theory suggests that there are three major factors that determine whether a reaction will occur:

The concentration of the activated complex

The rate at which the activated complex breaks apart

The way in which the activated complex breaks apart: whether it breaks apart to reform the reactants or whether it breaks apart to form a new complex, the products.

Collision theory proposes that not all reactants that combine undergo a reaction. However, assuming the stipulations of the collision theory are met and a successful collision occurs between the molecules, transition state theory allows one of two outcomes: a return to the reactants, or a rearranging of bonds to form the products.

Consider a bimolecular reaction:

where K is the equilibrium constant. In the transition state model, the activated complex AB is formed:

A + B  ⇌  AB^‡  →  C

There is an energy barrier, which is the activation energy, in the reaction pathway. A certain amount of energy is required for the reaction to occur. The transition state, AB^‡, is formed at maximum energy. This high-energy complex represents an unstable intermediate. Once the energy barrier is overcome, the reaction is able to proceed and product formation occurs.

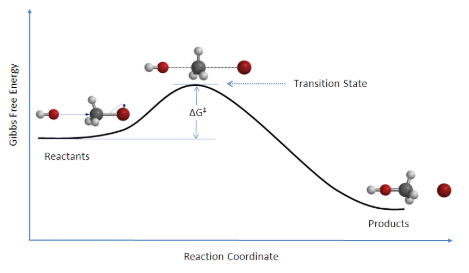
Reaction: HO^– + CH₃Br → [HO—CH₃—Br]^‡ → CH₃OH + Br

Figure 7.6.1. Reaction coordinate diagram for the bimolecular nucleophilic substitution (S_N2) reaction between bromomethane and the hydroxide anion. Image used with permission from Wikipedia.

The change in free energy, ΔG, is equal to the sum of the enthalpy plus the product of the temperature and entropy of the system and will be taught later in physical chemistry. Additionally, an S_N2 reaction denotes the addition of the nucleophile and the departure of the leaving group which will be covered in organic chemistry II.

The rate of a reaction is equal to the number of activated complexes decomposing to form products. Hence, it is the concentration of the high-energy complex multiplied by the frequency of it surmounting the barrier.

rate = v[AB]‡ = v[A][B]K^‡

The rate can be rewritten:

Combining the above equations gives:

k[A][B] = v[A][B]K^‡

k = vK^‡

Equation 7.6.1 Thermodynamic Equilibrium Constant

where

v is the frequency of vibration,

k is the rate constant and

K‡ is the thermodynamic equilibrium constant.

Statistical mechanics (not shown) provides that the frequency, v, is equivalent to the thermal energy, k_BT, divided by Planck’s constant, h.

where

k_B is the Boltzmann’s constant (1.381 x 10^-23 J/K),

T is the absolute temperature in Kelvin (K) and

h is Planck’s constant (6.626 x 10^-34 Js).

Substituting the equation for v into the equation for k:

k = k_BThK^‡

The equation for k is often tagged with another term (M^1−m) that makes the units equal with M is the molarity and m is the molecularly of the reaction.

It is important to note here that the equilibrium constant K‡ can be calculated by absolute, fundamental properties such as bond length, atomic mass, and vibration frequency. This gives the transition rate theory the alternative name absolute rate theory, because the rate constant, k, can be calculated from fundamental properties.

A balanced equation for a chemical reaction indicates what is reacting and what is produced, but it reveals nothing about how the reaction actually takes place. The reaction mechanism (or reaction path) is the process, or pathway, by which a reaction occurs.

A chemical reaction usually occurs in steps, although it may not always be obvious to an observer. The decomposition of ozone, for example, appears to follow a mechanism with two steps:

We call each step in a reaction mechanism an elementary reaction. Elementary reactions occur exactly as they are written and cannot be broken down into simpler steps. Elementary reactions add up to the overall reaction, which, for the decomposition, is:

2O₃ (g)  →  3O₂ (g)

Notice that the oxygen atom produced in the first step of this mechanism is consumed in the second step and therefore does not appear as a product in the overall reaction. Species that are produced in one step and consumed in a subsequent step are called intermediates.

While the overall reaction equation for the decomposition of ozone indicates that two molecules of ozone react to give three molecules of oxygen, the mechanism of the reaction does not involve the collision and reaction of two ozone molecules. Rather, it involves a molecule of ozone decomposing to an oxygen molecule and an intermediate oxygen atom; the oxygen atom then reacts with a second ozone molecule to give two oxygen molecules. These two elementary reactions occur exactly as they are shown in the reaction mechanism.