Questions

Chapter 1 – Stoichiometry

Learning objectives in the chapter:

• The mole
  • # of moles, atoms…
  •  Finding mass and molar mass
• Determining chemical formulae
  • molecular/empirical formula
  • % composition
  • Balancing equations/making equations
• Reaction stoichiometry
  • Limiting reagents
  • Rest is similar to the 2 topics above
• Solution stoichiometry
  • Molarity and molality
  • % by mass, volume…
• Redox reactions
  • Oxidation states
  • Half reaction – basic and acidic conditions

Questions:

1. The percent composition of an unknown gas is 41.95% C, 22.35% O, 29.36% N, et 6.34% H. What is the empirical formula of the unknown gas?
2. Balance the following chemical equation, using half-reactions, in basic conditions:

   MnO₄ (aq) + C₆H₁₂O₄ (aq) → Mn²⁺ (aq) + HCO₃ (aq)

    

3. An aqueous solution with a percent by mass of 20.0% for C₂H₅OH (C₂H₅OH is the only solute). The density of the solution is 0.945 g/mL. Calculate the molarity, molality and the mole fraction of C₂H₅OH in the solution.
4. The following unbalanced reaction, showing the oxidation of ethane to acetic acid by hydrogen peroxide, uses specialized iron-based catalysts:

   CH₃CH₃ (g) + H₂O₂ (l) à CH₃COOH (l) + H₂O (l)

   Unfortunately, there is a competing side reaction, in which the hydrogen peroxide decomposes to water and gaseous oxygen:

   H₂O₂ (l) → ½ O₂ (g) + H₂O (l)

   In a test experiment, 15.0 g of oxygen formed when 200.0 g of each reactant was used/ What is the highest possible percent yield of acetic acid that can be expected?

5. Out of Na (s), Na⁺ (aq), NaCl (s), Cl₂ (g) and Cl^– (aq), which of the following is an oxidant?
6. What is the oxidation state of C in HCN (note that carbon is the central atom, H is the least electronegative of the three and N is the most electronegative of the three)?
7. 205.0 g of H₂O, 225.0 g of O₂ and 240.0 g of P₄ reaction together based on the following equation:

   6 H₂O + 5 O₂ + P₄ → 4 H₃PO₄

   What is the mass (in grams) of H3PO4 produced? What is the mass (in grams) total of the excess reagents that did not react?

8. Walmart sells antifreeze, an aqueous solution that is 28.6% ethylene glycol (C₂H₆O₂) by mass. If the density of this solution is 1.03 g/cm³, calculate its molality.
9. An environmental chemist is analyzing a hydrocarbon pollutant in an Ontario lake. Elemental analysis shows that the hydrocarbon contains exclusively 85.63% carbon and 14.37% hydrogen, by mass. Using a mass spectrometer, she determines that the molecular mass of the pollutant is 70.13 amu. She then performs a redox reaction in order to quantify the exact concentration of the pollutant in the lakewater. She takes exactly 10.00 mL of lakewater and dilutes it to 50.00 mL using a volumetric flask and pure distilled water from the lab. She then uses a strong oxidizing agent, permanganate anions (MnO₄^–) to fully oxidize the hydrocarbon to gaseous carbon dioxide (the permanganate anions are reduced to Mn²⁺ aqueous ions). The reaction requires 46.43 mL of a 1.17×10^–4 M aqueous permanganate solution to complete. What is the concentration of the pollutant in the lakewater, in mol/L?
10. A salesman comes to your door and tells you that the tap water in your neighbourhood has recently been tested and high levels of lead (Pb) have been found. He can sell you a purification device for $7500 that can attach to your tap and remove the lead ions from the water. He wants to test your water to see if it is needed; all he needs from you is a small sample of tap water (100.0 mL).
    1. His test kit uses the following half reactions to test for the lead ions. Find the overall balanced redox reaction, under basic conditions (including phases).
       1. Pb²⁺(aq)  →  Pb (s)
       2. CN^–(aq)  →  CNO^– (aq) 
    2. Identify the oxidizing agent and the reducing agent in your reaction above.
11. Which compound has the highest oxidation state of nitrogen:
    1. NO⁺
    2. N₂
    3. NO₃^–
    4. NO₂
    5. N₂O
    6. NH₃
12. Complete combustion of a 1.119 g sample of an unknown gaseous compound (consisting of C, H, and S) yields 2.020 g of CO₂, 0.689 g of H₂O, and some SO₂.
    1. Find the number of moles of each element in the sample.
    2. What is the empirical formula of the compound?

Chapter 2 – Gases

Learning objectives in Chapter 2:

• Intermolecular forces
  • Identifying forces and explaining their relative strengths/behaviour in a molecule
• Gases and periodic table
  • Trends
• Measuring variable of gases
  • Intro to PV=nRT
  • Changing from bar to atm …
• Gas Laws *experiment 1*
  • Uses of different laws and applying them
  • PV=nRT and use n to calculate mass…
• Gas mixtures and Partial pressures
  • Finding molar mass from PV=nRT and mass
  • Determining molecular formulas
  • Partial pressures
• Kinetic-molecular theory of gases (ideal gas behaviour)
  • Behaviours explained
  • Root mean squared
  • Average kinetic energy
• Diffusion and effusion
  • Explaining these 2 concepts and applying them
• Real/non-ideal gas behaviours
  • explaining /applying concepts to questions and graphs

Questions:

1. If we react 88.8 g of C₂H₅OH (l) and 88.8 g of O₂ (g) in a combustion reaction producing CO₂ (g) and H₂O (l).  The combustion is held in a 10.0 L steel container and the temperature is fixed at 25.00०C. What is the mass of CO₂ (g) produced? Ignoring the vapour pressures of C₂H₅OH (l) and H₂O (l), what is the total pressure (in atm) before and after the reaction? (hint: these two values are not necessarily the same) Finally, what is the average speed of the CO₂ (g) molecules at the end of the reaction?
2. The percent composition of an unknown gas is 40.84% C, 20.40% O, 29.77% N and 9.00% H. What is the empirical formula? If the unknown gas has a density of 11.07 g/L a temperature of 777 K and a pressure of 1.00 atm, what is the molecular formula?

3. A general chemistry student wishes to compare the accuracy of the Ideal Gas Law versus Graham’s Law by performing two experiments.

   In the first experiment, he weighs a clean, evacuated round bottom flask (with its stopper) on a precision scale in the laboratory. He then completely fills the flask with distilled water, add the stopper, and weighs the flask again. The flask is then emptied, dried, filled a second time with argon gas and weighed. 

   In the second experiment, he sets up an effusion apparatus (similar to what is described in this chapter) to compare the rates of effusion of argon and nitrogen gas, using equimolar amounts of each gas at identical temperatures. 

   The data for both experiments are summarized in the table below. 

   

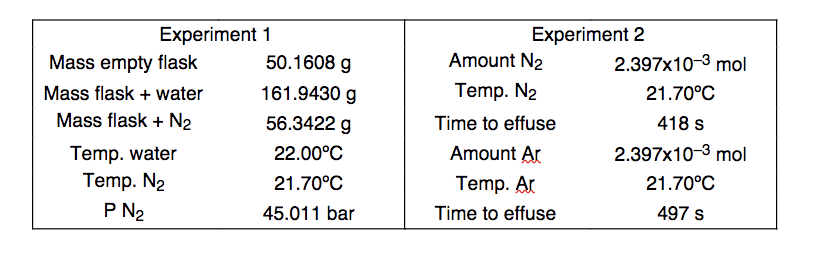
   Determine the molar mass of nitrogen using each set of data, then comment on the relative accuracy of the two equations (hint: you will require a data point from Appendix F). Can you explain your conclusion?

    

4. In a 33.3 L steel container, there is 88.8g CO₂ (g), 77.7g of N₂ (g), and some O₂ (g). The temperature is 25०C and the pressure is 5.555 atm. What is the molar mass of O₂ (g).
   1. Mass by volume of a sample of only CO₂ (g) is 1.55 g/L. The pressure is 2.22 atm. What is the average speed of the CO₂ (g) molecules?
5. In a 10.0 L steel container, we have 19.9 g of N₂ (g). The pressure is 2.50 atm. What is the average speed of the N₂ (g) molecules? Let’s say we add 19.9 g of O₂ (g) in the container. The temperature is adjusted to 25०C and the volume is fixed at 10.0 L. What is the total pressure?
6. A one litre balloon is filled with neon gas. A hole is made in the balloon and the gas effuses at a rate of 0.0280 mol/hr. If the same balloon is refilled with argon at the same pressure and temperature, its rate of effusion would be ____________.
7. The ideal gas law works best at low temperatures and high pressures. Circle the correct answer.
   1. True
   2. False
8. When Dr. Fox goes scuba diving, she uses NITROX, a special blend of enriched air that allows for more repetitive dives by reducing the build-up of nitrogen in the blood (that way, she won’t get “the bends”!). The local scuba shop prepares 7.20 L tanks of NITROX by mixing 25.0 g of O₂ with 42.0 g of N₂ at a temperature of 25.0^oC. What is the mole fraction of each gas in the mixture? What is the partial pressure of each gas, in bar?
9. Your chemistry professor decides to demonstrate Boyle’s law while scuba diving. She takes a syringe filled with 18.0 mL of air from the surface (which is at an atmospheric pressure of 1.014 bar and a temperature of 25.95ºC) with her on a dive to an unknown depth.
   • a) During the dive, the volume of the air in the syringe drops to 5.40 mL. What is the change in pressure at this unknown depth, in bars?
   • b) Scuba divers are taught that pressure increases by exactly 1 bar for every 10 m of depth. What was the depth of your professor’s dive, in metres?
   • c) If the mol fraction of oxygen in air is 0.209, calculate the number of moles of oxygen in the syringe.
10. The following reaction, occurring in a sealed vessel, has a percent yield of 94.9%:  2 NaN₃ (s)→2 Na (l) +3N₂ (g)
    1. What volume of N₂, measured at 735 mmHg and 26.0^oC, is produced when 75.0 g of sodium azide decomposes?

Chapter 3 – Thermochemistry

Learning objectives in Chapter 3:

• Introduction to thermochemistry
  • Conservation of energy
  • System, surroundings, universe
• Types of energy
  • exothermic/endothermic
  • Internal energy
  • -q = q
• First law of thermodynamics
  • Internal energy continued
  • Introduction of work and enthalpy
• Enthalpy
  • Enthalpy, q= mc∆T
  • Looking for different variables using variations of the enthalpy equation
• Calorimetry
  • Calculations in isolation (in a calorimeter)
• Hess’ Law

Questions:

1. In a bomb calorimeter with a constant volume, we combusted 1.22 g of C₆H₁₀O (l) (hint: the combustion is a reaction with a substance reacting with O_2(g) to produce CO₂ (g) and H₂O (l)). The bomb calorimeter has a heat capacity of 3.50 kJ K^-1 and is containing 2.725 kg of water. The specific heat capacity of water is 4.184 J K^-1 g^-1. The temperature of the calorimeter and the water raises from 20.50०C to 23.25०C. With this given information, calculate Q, W, ∆H and ∆U if we did combustion with one mole of C₆H₁₀O (l) under constant pressure of 1.00 bar at 25.00०C.
2. a) We place 100.0 g of 100.00०C metal in 222.2 g of water which is 10.00०C. The water is in a cup that is at the same temperature as the water. The heat capacity of the cup is 500 J K^–1. The final temperature of the metal, water and the cup are 13.33०C. What is the specific heat capacity of the metal? b) The combustion of one mole of methane (CH₄ (g)) releases 891 kJ of heat. We want to heat 6.66 kg of water from 20.00०C to 30.00०C. If the methane is at 25.0०C and has a pressure of 1.00 atm, which volume of CH₄ (g) should we have?
3. We have 437 g of water in a container. The temperature of the water and of the container is 23.0०C. We have a piece of iron weighing 122g at a temperature of 57.0०C and we place it in the water of the container. The specific heat capacities a the water and iron are 4.184 J K^-1 g^-1 and 0.44 J/ (g ०C) respectively. The heat capacity of the container is 217 J/०C. What is the final temperature of the water, iron and container?
4. With the given information:Calculate the values for ∆U and ∆H for the formation of one mole of CH₃OH (g):
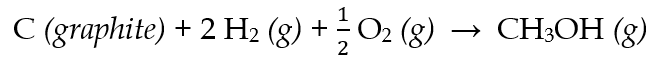
5. When the power was turned off to a 125 L water heater, the temperature of the water dropped from 75.0^oC to 22.5^oC. The amount of heat, in kilojoules, transferred to the surroundings was: _______________.
6. This past summer, Dr. Fox went scuba diving in False Bay, South Africa, where the water temperature was a chilly 13.5^oC. Despite wearing two 5 mm thick neoprene wetsuits, Dr. Fox still lost body heat at a rate of 38.0 J per second. How much body heat, in kJ, was lost over the course of a 45.0 min dive?
7. For the following reaction: 2 C₂H₆ (g) +7 O₂ (g)  →  4 CO₂ (g) + 6 H₂O (l)                ∆H=-3119kJ
   1. How much heat, in kJ, is associated with the combustion of 10.0 g of ethane?
   2. What is the quantity of work, in kJ, evolved in the combustion of 10.0 g of ethane at 25.00^oC? (Assume an exact stoichiometric quantity of oxygen is present).
8. A first-year student uses a fitness tracker to estimate the number of Calories burned while exercising. According to their fitness app, based on their current height and weight, they will burn approximately 8.5 Calories per min while jogging.
   1. How much energy, in kJ, is consumed over the course of a 25.0 min jog?
   2. To recuperate this energy loss, the student decides to eat a candy bar, which contains glucose, C6H12O6. Using the data in the Appendices, determine the enthalpy of combustion of glucose, in kJ/mol.
   3. If the candy bar contains 27.5% glucose (and similar sugars) by mass, how many grams of it will they need to eat to balance out the energy lost in part (a)? 
9. Consider the following hypothetical reaction: 

 

a) How much heat, in J, is associated with the reaction of 2.00 g of reactant A? 

b) What is the quantity of work, in J, evolved in the reaction of 2.00 g of reactant A at 55.80ºC? 

c) Calculate the change in internal energy for the reaction of 2.00 g of reactant A. 

d) Classify the reaction according to one of the following categories: 

i) EXOTHERMIC CONTRACTION

ii)ENDOTHERMIC CONTRACTION

iii) EXOTHERMIC EXPANSION

iv) ENDOTHERMIC EXPANSION 

e) Sketch an energy diagram for the reaction of 2.00 g of reactant A. In your diagram, label your axis and U1, U2, q, W, and ∆U. 

Learning objectives in Chapter 4:

• Introduction to chemical equilibrium
  • Written answers to questions – about reversibility, rate constants…
• The equilibrium constant and reaction quotient
  • Intro to K (when it is bigger or smaller than 1 and what that means) and Q (what that represents)
  • Q and K together in questions – what way will the equilibrium shift
• Solving equilibrium problems
  • K and Kp questions
  • Finding concentration and partial pressures
• Le Chatelier’s principle
  • Effects on equilibrium based on what is changed and is explained via the principle.

Questions:

1. 1. For the reaction 2 A (aq) → 2 B (aq) + C (aq), the equilibrium constant is 2.22 at 25.0०C. If the concentrations of B (aq) and C (aq) are 0.277 M and 0.444 M respectively, what is the concentration of A (aq) necessary to have free energy, G, of -5.00 kJ? Note that the temperature is always 25.0०C.
   2. For the reaction 2 A (g) → 2 B (g) + C (g), we only start with A (g) and B (g), and the partial pressure of A is double that of B. There is no C (g). The total pressure originally is 6.00 atm. We reach equilibrium. The finale pressure is now 6.80 atm. What is the value of G०for this reaction. Note that the temperature is always 25.0०C.
2. For the reaction A (aq) + B (aq) → 2 C (aq), the value of G०is +4.77 kJ (or kJ/mol) at 25.0०C. The initial concentrations for A (aq), B (aq) and C (aq) are 0.322 M, 0.244 M and 0.455 M respectively. What is the concentration of C (aq) once we reach equilibrium at 25.0०C?
3. The formation constant, K_f, of Ag(CN)2- is 3.0 x 10²⁰. We put 6.66 g of AgNO₃ in a 1.000 L of a 0.800 M solution with CN^–. assume the volume remains fixed at 1.000 L. What are the concentrations of Ag⁺ (aq), CN^– (aq) and Ag(CN)₂^– at equilibrium? The reaction involved: Ag⁺ (aq) + 2 CN^– (aq)  → Ag(CN)₂^– (aq)
4. Consider the following reaction:  A (g)  + 2 B (g)  ⇌  2 C (g), To a 2.50 L flask, A and B are added at initial pressures of 0.500 bar each. The mixture was allowed to equilibrate at 1000 K and the flask was found to contain 0.0147 mol of C.
   1. How much heat, in kJ, is associated with the combustion of 8.50 g of ethane?
   2. What is the quantity of work, in kJ, evolved in the combustion of 8.50 g of ethane at 25.00^oC? (Assume an exact stoichiometric quantity of oxygen is present).
5. Consider the following gaseous reaction:
   1. 
   2. An equimolar mixture of CH₄ and CO₂, with a total pressure of 20.0 bar, are placed in a 1.00 L flask and allowed to equilibrate at 1200 K. At equilibrium, the flask is found to contain 19.6 bar of hydrogen. What is the value of K of the reaction?
6. Given the information below, the value of the equilibrium constant for the reaction:
   1. A (g)  + 2 B (g)  ⇌  2 C (g) is:
   2. 2 A (g)  ⇌  2 X (g)  Kp  = 35.5 
   3. 2 C (g)  ⇌  X (g) + B (g)  Kp  = 7.2

Chapter 5 – Acid/Base Equilibria

Learning objectives in Chapter 5: 

• Acid-base definitions and conjugate acid-base pairs
  • Identifying conjugate and labelling an equation with acid-base pairing
• Autoionization of water and pH/pOH
  • Amphiprotic species
  • pH and pOH calculations
  • Ion concentration calculations
• Acid/Base strength
  • Strength of species identified based on behaviour/structure, and comparing its strength to other compounds
  • Ka/Kb calculations
  • Equilibrium concentration calculations
• Polyprotic acids
  • Calculating concentrations with the multiple Ka and Kb values
• Acid strength of hydrides and oxoacids
• Hydrolysis of salt solutions
  • Classifying salts as neutral, acidic or base
• Lewis acid and bases
  • Drawing lewis structures

Questions:

1.  NH₃ (aq) is a weak base with a dissociation constant, K_b, of 1.8 x 10^-5. What is the pH of an aqueous solution 0.333 M in NH₄Cl?
2. At 25.0०C, we place 2.33 g of acid, HA, in enough water to produce 25.0 mL of solution. The original pH is 1.44. We titrate this solution with a 0.222 M solution of NaOH and we need 22.2 mL to reach the equivalence point.
   1. What is the molar mass of HA?
   2. What is the ionization constant, K_a, of HA?
   3. What would the pH be of a 2.000 M solution in NaA?
   1. For the following reaction 2 A (aq)  ⇌  B (aq) + C (aq), the equilibrium constant is 5.55 at 25.0०C. The initial concentrations for A (aq), B (aq) and C (aq) are 0.444 M, 0.555 M and 0.666 M respectively. What is the concentration of A (aq) at equilibrium at 25.0०C?
   2. We have a 666 mL aqueous solution of NaOH. we add an excess of AL(NO₃)₃ to produce the precipitate Al(OH)₃ (s). We produce 0.0888 g of Al(OH)₃ (s). What was the original pH of the solution?
3. After a vacation of scuba-diving, Dr. Fox has to clean and rinse all her scuba gear before putting it back into storage. She wants to use “Diver’s Buddy Scuba Shampoo”, a commercially available aqueous solution of trimethylamine (N(CH₃)₃, K_b = 6.31 x 10^–6). Dr. Fox measures the pH of the solution and finds it to be 10.55. What is the concentration of trimethylamine in the shampoo, in mol/L?
4. You are performing a titration of 80.0mL of 0.0900 M HCN with 0.0900 M NaOH. Determine the pH of the solution:
   1. Initially
   2. At the half-equivalence point
   3. At the equivalence point
   4. Use these values to sketch a titration curve on the graph provided.
   5. 

 

Chapter 6 – Ionic Equilibria in Aqueous Systems (JT)

Topics discussed include:

• Common ion effect
  • Ksp questions and using Ksp to find concentrations
• Buffer solutions *experiment 3*
• Acid-base reactions and titrations *experiment 4*
• Equilibria of slightly soluble ionic compounds
  • Ksp and predicting precipitations

Questions:

1. The solubility constant for Mg(PO₄)₂ is 1.0 x 10-24. Calculate the solubility (in g/L) of Mg(PO₄)₂ in
   1. Pure water
   2. A 0.30 M solution of Mg(NO₃)₂
2. We prepare a buffer solution by reacting 12.1 g of NH₃ and 6.2 g of HCl in enough water to produce 1.000 L of solution. The ionization constant for the weak base (NH₃) is 1.8×10^-5.
   1. What is the pH of the solution?
   2. What would the pH of the solution be if we would add 1.00 g of NaOH (assume that the volume remains the same)?
   3. What would the pH of the solution if we would add 1.00 g of HCl (assume that the volume remains the same)?
3. What volume of a 0.277 M solution is needed to add to acetic acid, CH₃COOH, to neutralize 28.0 mL of a 0.348 M solution of Ba(OH)₂? Ba(OH)₂ is a strong base and acetic acid is a weak acid with a pKa of 4.74. What is the pH of the solution at the equivalence point?
4. The ionization constant for acetic acid, CH₃COOH, is 1.8 x 10-5. What is the pH of a solution if we add 0.847 g of sodium acetate, CH₃COONa, to pure water and the final volume is 100.0 mL.
5. You wish to prepare a buffer solution with pH = 9.45.
   1. How many grams of (NH₄)2SO₄ would you add to 425 mL of 0.258 M NH₃ to do this? You may assume that the solution’s volume remains constant. K_b of NH₃ = 1.8×10^-5
   2. You have access to additional 0.258 M NH₃ and more solid (NH₄)2SO₄. Which buffer component, and how much (in g or mL) would you add to 0.100 L of the buffer in part (a) to change its pH to 9.30? You may assume that the solution’s volume remains constant.
6. A student mixes 31.0 mL of 2.74 M Pb(NO₃)₂ (aq) with 20.0 mL of 0.00163 M NaI (aq).
   1. Identify the expected precipitate
   2. What are the values of [Pb²⁺], [Na⁺], [NO₃^–] and [I^–] after the solution has reached equilibrium at 25^oC? You may assume volumes are additive.
7.  From the list below, circle the basic salts and underline the neutral salts
   1. KCl
   2. FeCl₃
   3. NH₄Br
   4. Ca(CN)₂
   5. LiF
   6. CuNO₃