2.5 – Gas Mixtures and Partial Pressures
In our use of the ideal gas law thus far, we have focused entirely on the properties of pure gases with only a single chemical species. But what happens when two or more gases are mixed? In this section, we describe how to determine the contribution of each gas present to the total pressure of the mixture.
The Pressure of a Mixture of Gases: Dalton’s Law
In gas mixtures, each component in the gas phase can be treated separately. Each component of the mixture shares the same temperature and volume. (Remember that gases expand to fill the volume of their container; gases in a mixture do that as well.) However, each gas has its own pressure. Unless they chemically react with each other, the individual gases in a mixture of gases do not affect each other’s pressure. Each individual gas in a mixture exerts the same pressure that it would exert if it were present alone in the container (Figure 2.5.1). The pressure exerted by each individual gas in a mixture is called its partial pressure, denoted Pi. This observation is summarized by Dalton’s law of partial pressures: The total pressure of a mixture of ideal gases is equal to the sum of the partial pressures of the component gases:
PTotal = PA + PB + PC + … = ΣiPi
Equation 2.5.1. Dalton’s law of partial pressures.
In the equation, PTotal is the total pressure of a mixture of gases, PA is the partial pressure of gas A; PB is the partial pressure of gas B; PC is the partial pressure of gas C; and so on.
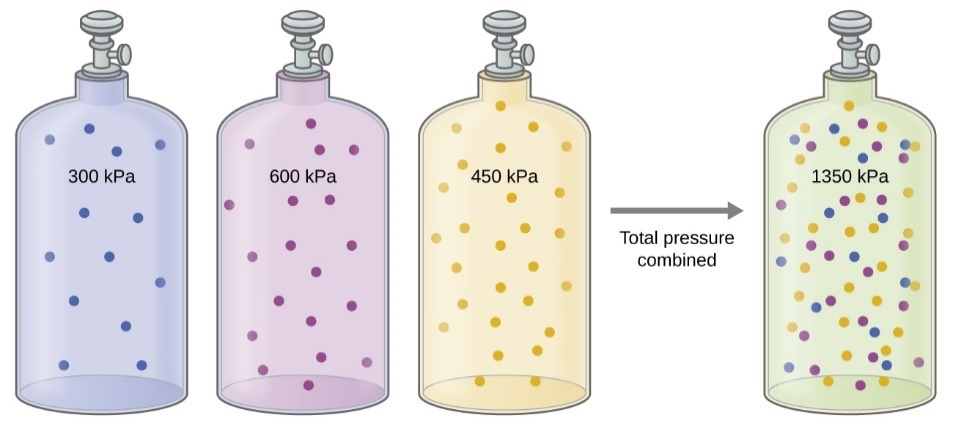
Figure 2.5.1. If equal-volume cylinders containing gas A at a pressure of 300 kPa, gas B at a pressure of 600 kPa, and gas C at a pressure of 450 kPa are all combined in the same-size cylinder, the total pressure of the mixture is 1350 kPa.
In this scenario of gas mixtures, volume and temperature are held constant because the gas are mixed together in one container (same fixed volume) in the same surroundings (same temperature). In that case, the ideal gas equation can be rearranged to show that the pressure of a sample of gas is directly proportional to the number of moles of gas present:
![]()
Nothing in the equation depends on the nature of the gas—only the amount.
Hence, if we have, for example, a mixture of two ideal gases, A and B, we can write an expression for the total pressure as:
![]()
More generally, for a mixture of n component gases, the total pressure is given by
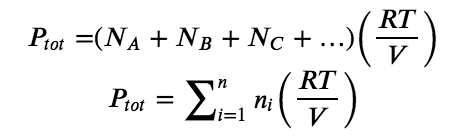
Mole Fractions of Gas Mixtures
The partial pressure of gas A is related to the total pressure of the gas mixture via its mole fraction (X), a unit of concentration defined as the number of moles of a component of a solution divided by the total number of moles of all components:
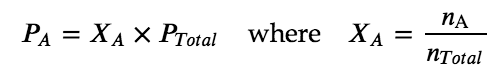
where PA, XA, and nA are the partial pressure, mole fraction, and number of moles of gas A, respectively, and nTotal is the number of moles of all components in the mixture.
Example 2.5.1 – The Pressure of a Mixture of Gases
A 10.0 L vessel contains 2.50 × 10−3 mol of H2, 1.00 × 10−3 mol of He, and 3.00 × 10−4 mol of Ne at 35 °C.
(a) What are the partial pressures of each of the gases?
(b) What is the total pressure in atmospheres?
Solution
(a) The gases behave independently, so the partial pressure of each gas can be determined from the ideal gas equation, using P = nRT/ V :

(b) The total pressure is given by the sum of the partial pressures:
![]()
Check Your Learning 2.5.1 – The Pressure of a Mixture of Gases
A 5.73 L flask at 25 °C contains 0.0388 mol of N2, 0.147 mol of CO, and 0.0803
mol of H2. What is the total pressure in the flask in atmospheres?
Answer
1.14 atm
Here is another example of this concept, but dealing with mole fraction calculations.
Example 2.5.2 – The Pressure of a Mixture of Gases
A gas mixture used for anesthesia contains 2.83 mol oxygen, O2, and 8.41 mol nitrous oxide, N2O. The total pressure of the mixture is 192 kPa.
(a) What are the mole fractions of O2 and N2O? What are the partial pressures of O2 and N2O?
Solution
The mole fraction is given by ![]() and the partial pressure is PA = XA × PTotal.
and the partial pressure is PA = XA × PTotal.
For O2,
![]()
and:
![]()
For N2O,
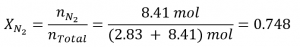
and:
Check Your Learning 2.5.2 – The Pressure of a Mixture of Gases
What is the pressure of a mixture of 0.200 g of H2, 1.00 g of N2, and 0.820 g of
Ar in a container with a volume of 2.00 L at 20°C?
Answer
1.87 atm
Collection of Gases over Water
The collection of gases over water by bubbling through it is one of the main reasons why we have to learn and understand Dalton’s law of partial pressures. This simple way of collecting gases that do not react with water involves capturing them in a bottle that has been filled with water and inverting into a dish filled with water. The pressure of the gas inside the bottle can be made equal to the air pressure outside by raising or lowering the bottle. When the water level is the same both inside and outside the bottle (Figure 2.5.2), the pressure of the gas is equal to the atmospheric pressure, which can be measured with a barometer.
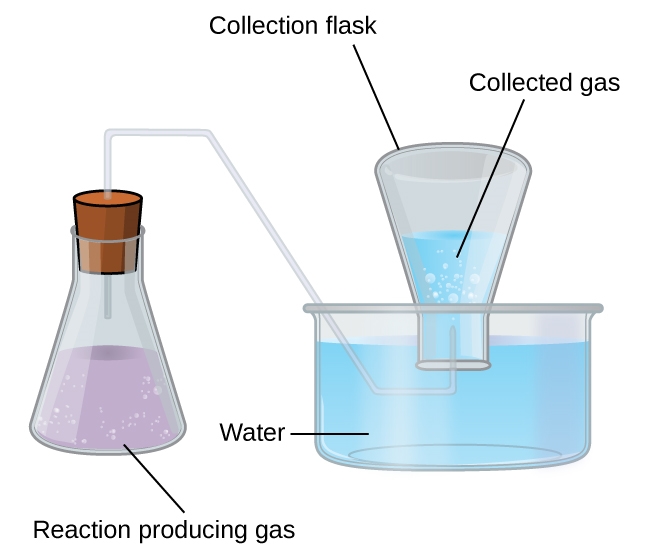
Figure 2.5.2. When a reaction produces a gas that is collected above water, the trapped gas is a mixture of the gas produced by the reaction and water vapour. If the collection flask is appropriately positioned to equalize the water levels both within and outside the flask, the pressure of the trapped gas mixture will equal the atmospheric pressure outside the flask (see the earlier discussion of manometers).
However, there is another factor we must consider when we measure the pressure of the gas by this method. Liquids, including water, have a property of constantly evaporating into a vapour until the vapour achieves a partial pressure characteristic of the substance and the temperature. This partial pressure is called a vapour pressure. Water evaporates and there is always gaseous water (water vapour) above a sample of liquid water. As a gas is collected over water, it becomes saturated with water vapour and the total pressure of the mixture equals the partial pressure of the gas plus the partial pressure of the water vapour. The pressure of the pure gas is therefore equal to the total pressure minus the pressure of the water vapour—this is referred to as the “dry” gas pressure, that is, the pressure of the gas only, without water vapour. The vapour pressure of water, which is the pressure exerted by water vapour in equilibrium with liquid water in a closed container, depends on the temperature (Figure 2.5.3); more detailed information on the temperature dependence of water vapour can be found in Table 2.5.1 below Figure 2.5.3.
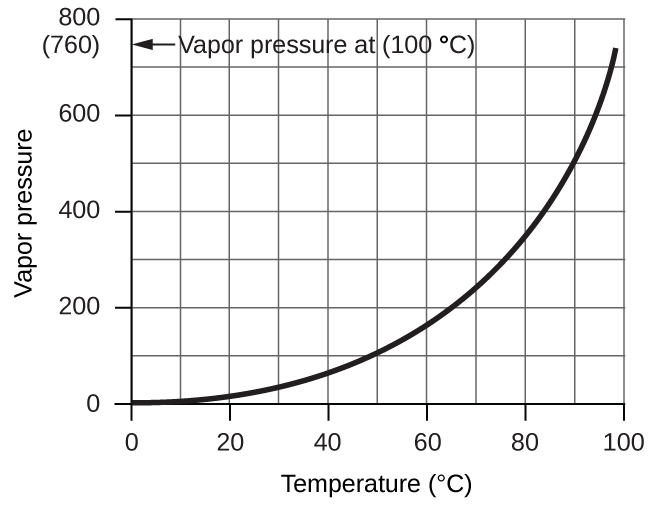
Figure 2.5.3. The vapour pressure of water at sea level as a function of temperature.
Table 2.5.1. Vapour pressure of ice and water in various temperatures at sea level.
|
Temperature (°C) |
Pressure (Torr) |
Temperature (°C) |
Pressure (Torr) |
Temperature (°C) |
Pressure (Torr) |
|
-10 |
1.95 |
18 |
15.48 |
30 |
31.82 |
|
-5 |
3.01 |
19 |
16.48 |
35 |
41.18 |
|
-2 |
3.88 |
20 |
17.54 |
40 |
55.32 |
|
0 |
4.58 |
21 |
18.65 |
50 |
92.51 |
|
2 |
5.29 |
22 |
19.83 |
60 |
149.38 |
|
4 |
6.10 |
23 |
21.07 |
70 |
233.7 |
|
6 |
7.01 |
24 |
22.38 |
80 |
355.1 |
|
8 |
8.04 |
25 |
23.76 |
90 |
525.76 |
|
10 |
9.21 |
26 |
25.21 |
95 |
633.90 |
|
12 |
10.52 |
27 |
26.74 |
99 |
733.24 |
|
14 |
11.99 |
28 |
28.35 |
100.0 |
760.00 |
|
16 |
13.63 |
29 |
30.04 |
101.0 |
787.57 |
| * CRC Handbook of Chemistry and Physics, 65th Edition. Cleveland, Ohio: CRC Press, 1984. | |||||
Example 2.5.3 – Pressure of a Gas Collected Over Water
If 0.200 L of argon is collected over water at a temperature of 26 °C and a pressure of 750 Torr in a system like that shown in Figure 2.5.2, what is the partial pressure of argon?
Solution
According to Dalton’s law, the total pressure in the bottle (750 Torr) is the sum of the partial pressure of argon and the partial pressure of gaseous water:
PT = PAr + PH2O
Rearranging this equation to solve for the pressure of argon gives:
PAr = PT – PH2O
The pressure of water vapour above a sample of liquid water at 26 °C is about 25.2 Torr (Appendix F), so:
PAr = 750 Torr – 25.2 Torr = 725 Torr
Check Your Learning 2.5.3 – Pressure of a Gas Collected Over Water
A sample of oxygen collected over water at a temperature of 29.0 °C and a
pressure of 764 Torr has a volume of 0.560 L. What volume would the dry
oxygen have under the same conditions of temperature and pressure?
Answer:
0.583 L
|
Food/Drink Application – Carbonated Beverages |
|
Carbonated beverages—sodas, beer, sparkling wines—have one thing in common: they have CO2 gas dissolved in them in such sufficient quantities that it affects the drinking experience. Most people find the drinking experience pleasant—indeed, in Canada alone in 2016, about 1/4 of those 5 to 19 years of age reported daily consumption of sugary drinks. Research shows that soda, energy and sports drinks are the top calorie source among North Americans ages 12 to 50. All carbonated beverages are made in one of two ways. First, the flat beverage is subjected to a high pressure of CO2 gas, which forces the gas into solution. The carbonated beverage is then packaged in a tightly sealed package (usually a bottle or a can) and sold. When the container is opened, the CO2 pressure is released, resulting in the well-known hiss, and CO2 bubbles come out of solution (Figure 2.5.4). This must be done with care: if the CO2 comes out too violently, a mess can occur!
Figure 2.5.4. If you are not careful opening a container of a carbonated beverage, you can make a mess as the CO2 comes out of solution suddenly. Source: “Champagne uncorking” by Niels Noordhoek is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license. The second way a beverage can become carbonated is by the ingestion of sugar by yeast, which then generates CO2 as a digestion product. This process is called fermentation. The overall reaction is: C6H12O6 (aq) → 2 C2H5OH (aq) + 2 CO2 (aq) When this process occurs in a closed container, the CO2 produced dissolves in the liquid, only to be released from solution when the container is opened. Most fine sparkling wines and champagnes are turned into carbonated beverages this way. Less-expensive sparkling wines are made like sodas and beer, with exposure to high pressures of CO2 gas. Source: Heart and Stroke Foundation. |
Questions
★ Questions
1. A cylinder of O2 (g) used in breathing by emphysema patients has a volume of 3.00 L at a pressure of 10.0 atm. If the temperature of the cylinder is 28.0 °C, what mass (in grams) of oxygen is in the cylinder?
2. What is the molar mass (in g⋅mol-1) of a gas if 0.0494 g of the gas occupies a volume of 0.100 L at a temperature 26 °C and a pressure of 307 Torr?
3. How could you show experimentally that the molecular formula of propene is C3H6, not CH2?
4. The density of a certain gaseous fluoride of phosphorus is 3.93 g/L at STP (where P = 1.00 bar, T = 273.15 K, 1 mole = 22.7 L). Calculate the molar mass (in g⋅mol-1) of this fluoride and determine its molecular formula.
5. What is the molecular formula of a compound that contains 39% C, 45% N, and 16% H if 0.157 g of the compound occupies 125 mL with a pressure of 99.5 kPa at 22 °C?
6. A cylinder of a gas mixture used for calibration of blood gas analyzers in medical laboratories contains 5.0% CO2, 12.0% O2, and the remainder N2 at a total pressure of 146 atm. What is the partial pressure (in bars) of each component of this gas? (The percentages given indicate the percent of the total pressure that is due to each component.)
7. A sample of gas isolated from unrefined petroleum contains 90.0% CH4, 8.9% C2H6, and 1.1% C3H8 at a total pressure of 307.2 kPa. What is the partial pressure (in bars) of each component of this gas? (The percentages given indicate the percent of the total pressure that is due to each component.)
8. A mixture of 0.200 g of H2, 1.00 g of N2, and 0.820 g of Ar is stored in a closed container at STP (where P = 1.00 bar, T = 273.15 K, 1 mole = 22.7 L). Find the volume of the container (in litres), assuming that the gases exhibit ideal behavior.
9. Calculate the volume (in litres) of oxygen required to burn 12.00 L of ethane gas, C2H6, to produce carbon dioxide and water, if the volumes of C2H6 and O2 are measured under the same conditions of temperature and pressure.
10. Methanol, CH3OH, is produced industrially by the following reaction:
CO (g) + 2 H2 (g) → CH3OH (g) (using a copper catalyst 300 °C, 300 atm)
Assuming that the gases behave as ideal gases, find the ratio of the total volume of the reactants to the final volume.
11. A 2.50-L sample of a colorless gas at STP decomposed to give 2.50 L of N2 and 1.25 L of O2 at STP. What is the colorless gas?
★★ Questions
12. Ethanol, C2H5OH, is produced industrially from ethylene, C2H4, by the following sequence of reactions:
3 C2H4 + 2 H2SO4 → C2H5HSO4 + (C2H5)2SO4
C2H5HSO4 + (C2H5)2SO4 + 3 H2O → 3 C2H5OH + 2 H2SO4
What volume (in litres) of ethylene at STP (where P = 1.00 bar, T = 273.15 K, 1 mole = 22.7 L) is required to produce 1.000 metric ton (1000 kg) of ethanol if the overall yield of ethanol is 90.1%?
★★★ Questions
13. A sample of a compound of xenon and fluorine was confined in a bulb with a pressure of 18 Torr. Hydrogen was added to the bulb until the pressure was 72 Torr. Passage of an electric spark through the mixture produced Xe and HF. After the HF was removed by reaction with solid KOH, the final pressure of xenon and unreacted hydrogen in the bulb was 36 Torr. What is the empirical formula of the xenon fluoride in the original sample? (Note: Xenon fluorides contain only one xenon atom per molecule.)
Answers
1. 38.8 g
2. 30.0 g mol-1
3. By doing an elevation in boiling point and a depression of freezing point as an experiment, one can find the exact molecular mass. As a result of that, the difference between propene and CH2 can be determined.
4. 88.1 g mol−1; PF3
5. (a) With the given percent compositions, one can assume a mass of 40 g C, 45 g N and 16 g H. Using this information, the empirical formula can be obtained by finding the moles of each atom making up the compound. From there, divide each mole value by the smallest amount of moles to get the makeup of the empirical formula. Calculate the molecular mass of the empirical formula based on its makeup as well as the molecular mass for the molecular formula with the given values in the question. Divide the molecular formula’s molecular mass by one of the one from the empirical formula. That ratio will determine if the makeup must be multiplied by that factor in order to determine the molecular formula.; (b) CNH5
6. CO2 = 7 atm, O2 = 18 atm, N2 = 120 atm
7. CH4: 276 kPa; C2H6: 27 kPa; C3H8: 3.4 kPa
8. 1.87 atm
9. 42.00 L
10. 3 : 1, if stoichiometric amounts are used
11. N2O
12. 5.40 × 105 L
13. XeF2
Pressure exerted by an individual gas in a mixture
Total pressure of a mixture of ideal gases is equal to the sum of the partial pressures of the component gases
Ratio of the molar amount of a mixture component to the total number of moles of all mixture components
Pressure exerted by water vapor in equilibrium with liquid water in a closed container at a specific temperature


