5.2 – Autoionization of Water & pH/pOH

The Autoionization of Water

In the preceding section we saw examples where water can function as either an acid or a base, depending on the nature of the solute dissolved in it. In fact, in pure water or indeed any aqueous solution, water acts both as an acid and a base. A very small fraction of water molecules donate protons to other water molecules to form hydronium ions and hydroxide ions:

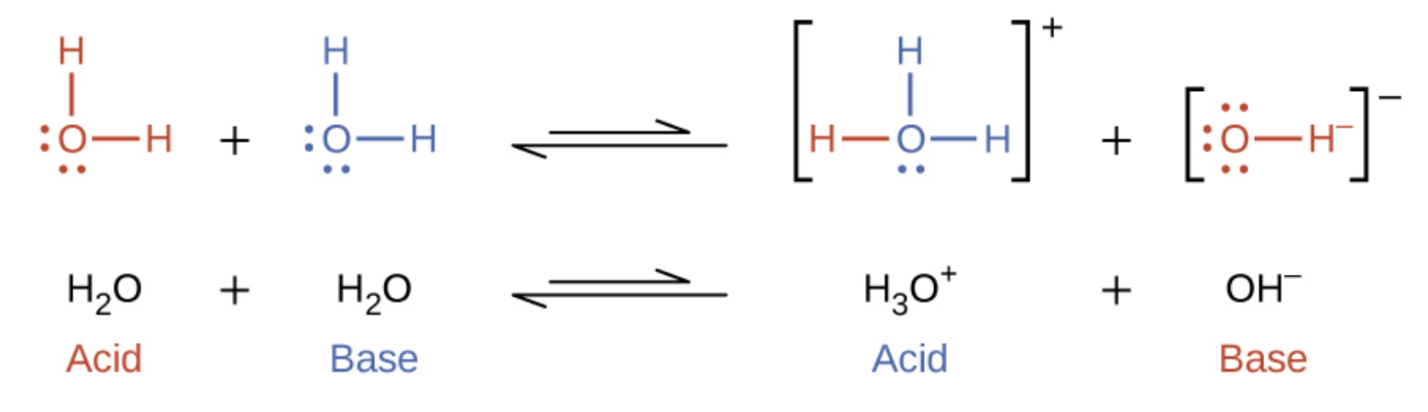
This type of reaction, in which a substance ionizes when one molecule of the substance reacts with another molecule of the same substance, is referred to as autoionization.

Pure water undergoes autoionization to a very slight extent. Only about two out of every billion (10⁹) molecules in a sample of pure water are ionized at 25 °C. The equilibrium constant for the ionization of water is called the ion-product constant for water (K_w):

H₂O (l) + H₂O (l) ⇌ H₃O⁺ (aq) + OH^– (aq)     K_w = [H₃O⁺][OH^–]

The slight ionization of pure water is reflected in the small value of the equilibrium constant; at 25 °C, K_w has a value of 1.0 × 10⁻¹⁴. The process is endothermic, and so the extent of ionization and the resulting concentrations of hydronium ion and hydroxide ion increase with temperature. For example, at 100 °C, the value for K_w is about 5.6 × 10⁻¹³, roughly 50 times larger than the value at 25 °C.

Example 5.2.1 – Ion Concentrations in Pure Water

What are the hydronium ion concentration and the hydroxide ion concentration in pure water at 25 °C?

Solution

The autoionization of water yields the same number of hydronium and hydroxide ions. Therefore, in pure water, [H₃O⁺] = [OH⁻]. At 25 °C:

K_w =[H₃O⁺][OH^–] = [H₃O⁺]² = [OH^–]² = 1.0×10^-14

So:

[H₃O⁺] = [OH-] = sqrt( 1.0×10^-14 ) =1.0×10^-7 M

The hydronium ion concentration and the hydroxide ion concentration are the same, and we find that both equal 1.0 × 10⁻⁷ M.

Check Your Learning 5.2.1 – Ion Concentrations in Pure Water

The ion product of water at 80 °C is 2.4 × 10⁻¹³. What are the concentrations of hydronium and hydroxide ions in pure water at 80 °C?

Answer

[H₃O⁺] = [OH⁻] = 4.9 × 10⁻⁷ M

It is important to realize that the autoionization equilibrium for water is established in all aqueous solutions. Adding an acid or base to water will not change the position of the equilibrium. The following example demonstrates the quantitative aspects of this relation between hydronium and hydroxide ion concentrations.

Example 5.2.2 – The Inverse Proportionality of [H₃O⁺] and [OH⁻]

A solution of carbon dioxide in water at equilibrium has a hydronium ion concentration of 2.0 × 10⁻⁶ M. What is the concentration of hydroxide ion at 25 °C?

Solution

We know the value of the ion-product constant for water at 25 °C:

2 H₂O(l)↔ H₃O⁺ (aq) + OH^– (aq)            K_w =[H₃O⁺][OH^–] = 1.0×10^-14

Thus, we can calculate the missing equilibrium concentration.

Rearrangement of the K_w expression yields that [OH⁻] is directly proportional to the inverse of [H₃O⁺]:

[OH^–] = K_w/[H₃O⁺] = (1.0×10^-14)/(2.0×10^-6 M) = 5.0×10^-9 M 

The hydroxide ion concentration in water is reduced to 5.0 × 10⁻⁹ M as the hydronium ion concentration increases to 2.0 × 10⁻⁶ M. This is expected from Le Châtelier’s principle; the autoionization reaction shifts to the left to reduce the stress of the increased hydronium ion concentration and the [OH⁻] is reduced relative to that in pure water. This is best visualized with a seesaw analogy, as shown in Figure 5.2.1.

A check of these concentrations confirms that our arithmetic is correct:

K_w = [H₃O⁺][OH^–] = (2.0×10^-6 M)(5.0×10^-9 M) = 1.0×10^-14

Figure 5.2.1. The ion-product constant is K_W = 1.0 × 10^-14 the whole time at 25°C. In pure water, [H₃O⁺] = [OH^–] = 1.0 × 10^-7. When we increase [H₃O⁺], like a seesaw, this is balanced and counteracted by a decrease in [OH^–] – this keeps K_W constant.

Check Your Learning 5.2.2 – The Inverse Proportionality of [H₃O⁺] and [OH⁻]

What is the hydronium ion concentration in an aqueous solution with a hydroxide ion concentration of 0.001 M at 25 °C?

Answer

[H₃O⁺] = 1 × 10⁻¹¹ M

Amphiprotic Species

Like water, many molecules and ions may either gain or lose a proton under the appropriate conditions. Such species are said to be amphiprotic. Another term used to describe such species is amphoteric, which is a more general term for a species that may act either as an acid or a base by any definition (not just the Brønsted-Lowry one). Consider for example the bicarbonate ion, which may either donate or accept a proton as shown here:

HCO₃⁻ (aq) + H₂O (l) ⇌ CO₃^2- (aq) + H₃O⁺ (aq)

HCO₃⁻ (aq) + H₂O (l) ⇌ H₂CO₃ (aq) + OH^– (aq)

Example 5.2.3 – Representing the Acid-Base Behavior of an Amphoteric Substance

Write separate equations representing the reaction of HSO₃⁻

(a) acting as an acid with OH⁻

(b) acting as a base with HI

Solution

HSO₃⁻(aq) + OH^– (aq) ⇌ SO₃^2-(aq) + H₂O (l)

HSO₃⁻(aq) + HI (aq) ⇌ H₂SO₃(aq) + I⁻(aq)

Check Your Learning 5.2.3 – Representing the Acid-Base Behavior of an Amphoteric Substance

Write separate equations representing the reaction of H₂PO₄⁻

(a) as a base with HBr

(b) as an acid with OH⁻

Answer

H₂PO₄⁻(aq) + HBr (aq) ⇌ H₃PO₄(aq) + Br⁻(aq)

H₂PO₄⁻(aq) + OH⁻ (aq) ⇌ HPO₄^2- (aq) + H₂O (l)

pH and pOH

As discussed earlier, hydronium and hydroxide ions are present both in pure water and in all aqueous solutions, and their concentrations are inversely proportional as determined by the ion product of water (K_w). The concentrations of these ions in a solution are often critical determinants of the solution’s properties and the chemical behaviors of its other solutes, and specific vocabulary has been developed to describe these concentrations in relative terms. A solution is neutral if it contains equal concentrations of hydronium and hydroxide ions; acidic if it contains a greater concentration of hydronium ions than hydroxide ions; and basic if it contains a lesser concentration of hydronium ions than hydroxide ions.

A common means of expressing quantities, the values of which may span many orders of magnitude, is to use a logarithmic scale. One such scale that is very popular for chemical concentrations and equilibrium constants is based on the p-function, defined as shown where “X” is the quantity of interest and “log” is the base-10 logarithm:

pX = -log(X)

The pH of a solution is therefore defined as shown here, where [H₃O⁺] is the molar concentration of hydronium ion in the solution:

pH =-log[H₃O⁺]

Rearranging this equation to isolate the hydronium ion molarity yields the equivalent expression:

[H₃O⁺]= 10^-pH

Likewise, the hydroxide ion molarity may be expressed as a p-function, or pOH:

pOH = -log[OH^–]

or

[OH^–] = 10^-pOH

Finally, the relation between these two ion concentrations expressed as p-functions is easily derived from the K_w expression:

K_w =[H₃O⁺][OH^–]

-log(K_w) =-log([H₃O⁺][OH^–])= -log[H₃O⁺]+-log[OH^–]

pK_w=pH+pOH

At 25 °C, the value of K_w is 1.0 × 10⁻¹⁴, and so:

14.00 = pH + pOH

As was shown in the reaction of a Brønsted-Lowry acid with water, the hydronium ion molarity in pure water (or any neutral solution) is 1.0 × 10⁻⁷ M at 25 °C. The pH and pOH of a neutral solution at this temperature are therefore:

pH= -log [H₃O⁺]=-log (1.0×10^-7)= 7.00

pOH= -log[OH-]=-log (1.0×10^-7)= 7.00

And so, at this temperature, acidic solutions are those with hydronium ion molarities greater than 1.0 × 10⁻⁷ M and hydroxide ion molarities less than 1.0 × 10⁻⁷ M (corresponding to pH values less than 7.00 and pOH values greater than 7.00). Basic solutions are those with hydronium ion molarities less than 1.0 × 10⁻⁷ M and hydroxide ion molarities greater than 1.0 × 10⁻⁷ M (corresponding to pH values greater than 7.00 and pOH values less than 7.00).

Since the autoionization constant K_w is temperature dependent, these correlations between pH values and the acidic/neutral/basic adjectives will be different at temperatures other than 25 °C (Figure 5.2.2). For example, the “Check Your Learning” exercise from the previous topic showed the hydronium molarity of pure water at 80 °C is 4.9 × 10⁻⁷ M, which corresponds to pH and pOH values of:

pH = -log[H₃O⁺] = -log(4.9×10^-7) = 6.31

pOH=-log[OH^–] = -log(4.9×10^-7) = 6.31

At this temperature, then, neutral solutions exhibit pH = pOH = 6.31, acidic solutions exhibit pH less than 6.31 and pOH greater than 6.31, whereas basic solutions exhibit pH greater than 6.31 and pOH less than 6.31. This distinction can be important when studying certain processes that occur at non standard temperatures, such as enzyme reactions in warm-blooded organisms.

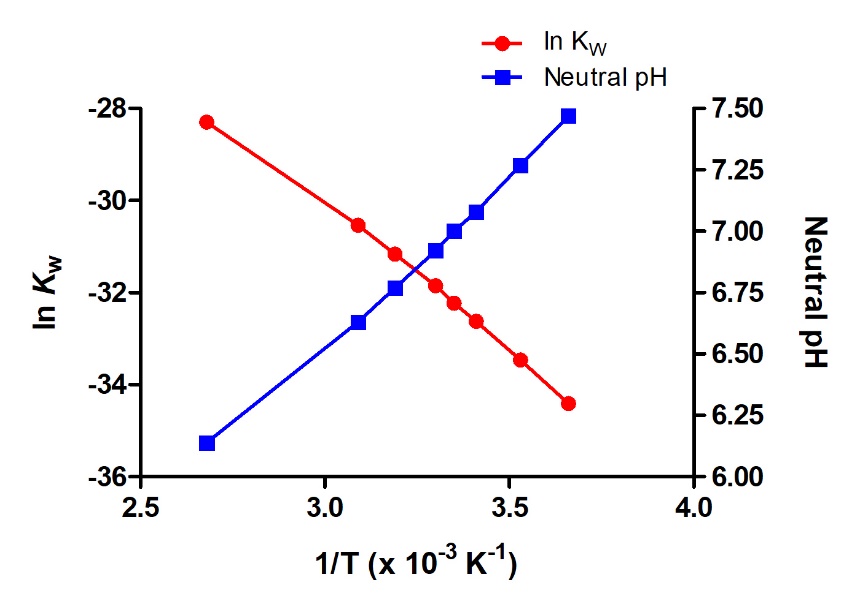
Figure 5.2.2. Like any other equilibrium constant, the autoionization constant, K_W, is temperature-dependent. Hence, a van’t Hoff plot can be constructed to see the variation of K_W over T. The graph also plots the variation of the pH of neutral pure water over varying temperatures.

Unless otherwise noted, references to pH values, such as those in Table 5.2.1 below, are presumed to be those at standard temperature (25 °C).

Table 5.2.1 Summary of Relations for Acidic, Basic, and Neutral Solutions

Figure 5.2.2.The pH and pOH scales represent concentrations of [H₃O⁺] and OH⁻, respectively. The pH and pOH values of some common substances at standard temperature (25 °C) are shown in this chart.

Example 5.2.4 – Calculation of pH from [H₃O⁺]

What is the pH of stomach acid, a solution of HCl with a hydronium ion concentration of 1.2 × 10⁻³ M?

Solution

(The use of logarithms is explained in Appendix C. Recall that, as we have done here, when taking the log of a value, keep as many decimal places in the result as there are significant figures in the value.)

Check Your Learning 5.2.4 – Calculation of pH from [H₃O⁺]

Water exposed to air contains carbonic acid, H₂CO₃, due to the reaction between carbon dioxide and water:

                                                                  CO₂ (aq) + H₂O (l) ⇌ H₂CO₃ (aq)

Air-saturated water has a hydronium ion concentration caused by the dissolved CO₂ of 2.0 × 10⁻⁶ M, about 20-times larger than that of pure water. Calculate the pH of the solution at 25 °C.

Answer

5.70

Example 5.2.4 – Calculation of Hydronium Ion Concentration from pH

Calculate the hydronium ion concentration of blood, the pH of which is 7.3 (slightly alkaline).

Solution

pH= -log[H₃O⁺] = 7.3

log[H₃O⁺]= -7.3

[H₃O⁺] = 10^-7.3 or [H₃O+] =antilog of -7.3

[H₃O⁺] = 5×10^-8 M

(On a calculator take the antilog, or the “inverse” log, of −7.3, or calculate

10^−7.3.)

Check Your Learning 5.2.5 – Calculation of Hydronium Ion Concentration from pH

Calculate the hydronium ion concentration of a solution with a pH of −1.07.

Answer

12 M

Environmental Science

Normal rainwater has a pH between 5 and 6 due to the presence of dissolved CO₂ which forms carbonic acid:

H₂O (l) + CO₂ (g) ⇌ H₂CO₃ (aq)

H₂CO₃ (aq) + H₂O(l) ⇌ HCO₃^– (aq) + H₃O⁺ (aq)

Acid rain is rainwater that has a pH of less than 5, due to a variety of nonmetal oxides, including CO₂, SO₂, SO₃, NO, and NO₂ being dissolved in the water and reacting with it to form not only carbonic acid, but sulfuric acid and nitric acid. The formation and subsequent ionization of sulfuric acid are shown here:

H₂O(l) + SO₃(g)  ⇌  H₂SO₄(aq)

H₂SO₄(aq) + H₂O(aq) → HSO₄^–(aq) + H₃O⁺(aq)

Carbon dioxide is naturally present in the atmosphere because we and most other organisms produce it as a waste product of metabolism. Carbon dioxide is also formed when fires release carbon stored in vegetation or when we burn wood or fossil fuels. Sulfur trioxide in the atmosphere is naturally produced by volcanic activity, but it also stems from burning fossil fuels, which have traces of sulfur, and from the process of “roasting” ores of metal sulfides in metal-refining processes. Oxides of nitrogen are formed in internal combustion engines where the high temperatures make it possible for the nitrogen and oxygen in air to chemically combine.

Acid rain is a particular problem in industrial areas where the products of combustion and smelting are released into the air without being stripped of sulfur and nitrogen oxides. In North America and Europe until the 1980s, it was responsible for the destruction of forests and freshwater lakes, when the acidity of the rain actually killed trees, damaged soil, and made lakes uninhabitable for all but the most acid-tolerant species. Acid rain also corrodes statuary and building facades that are made of marble and limestone (Figure 5.2.3.). Regulations limiting the amount of sulfur and nitrogen oxides that can be released into the atmosphere by industry and automobiles have reduced the severity of acid damage to both natural and manmade environments in North America and Europe. It is now a growing problem in industrial areas of China and India.

If you’re interested in this subject and want to learn more about this topic and/or other environmental topics and their relation to chemistry, the Department of Chemistry and Biomolecular Sciences of the Faculty of Science offers the course CHM 2313: Environmental Chemistry in the winter semester.

Figure 5.2.3. (a) Acid rain makes trees more susceptible to drought and insect infestation, and depletes nutrients in the soil. (b) It also corrodes statues that are carved from marble or limestone. (credit a: modification of work by Chris M Morris; credit b: modification of work by “Eden, Janine and Jim”/Flickr)

Example 5.2.5 – Calculation of pOH

What are the pOH and the pH of a 0.0125 M solution of potassium hydroxide, KOH?

Solution

Potassium hydroxide is a highly soluble ionic compound and completely ionizes when dissolved in dilute solution,

yielding [OH⁻] = 0.0125 M:

pOH =-log[OH^–] = -log(0.0125)

= -(-1.903)=1.903

The pH can be found from the pOH:

pH+pOH = 14.00

pH= 14.00-pOH = 14.00-1.903 =12.10

Check Your Learning 5.2.6 – Calculation of pOH

The hydronium ion concentration of vinegar is approximately 4 × 10⁻³ M. What are the corresponding values of pOH and pH?

Answer

pOH = 11.6, pH = 2.4

The acidity of a solution is typically assessed experimentally by measurement of its pH. The pOH of a solution is not usually measured, as it is easily calculated from an experimentally determined pH value. The most accurate way of ascertaining the pH of an acidic solution is by titration. The second most effective tool is by directly measuring using a pH meter (Figure 5.2.4.).

Figure 5.2.4. (a) A research-grade pH meter used in a laboratory can have a resolution of 0.001 pH units, an accuracy of ± 0.002 pH units, and may cost in excess of $1000. (b) A portable pH meter has lower resolution (0.01 pH units), lower accuracy (± 0.2 pH units), and a far lower price tag. (credit b: modification of work by Jacopo Werther)

The pH of a solution may also be visually estimated using coloured indicators (Figure 5.2.5.), which give the least accuracy in pH determination.

Figure 5.2.5. (a) A universal indicator assumes a different colour in solutions of different pH values. Thus, it can be added to a solution to determine the pH of the solution. The eight vials each contain a universal indicator and 0.1 M solutions of progressively weaker acids: HCl (pH = 1), CH₃CO₂H (pH = 3), and NH₄Cl (pH = 5), deionized water, a neutral substance (pH = 7); and 0.1 M solutions of the progressively stronger bases: KCl (pH = 7), aniline, C₆H₅NH₂ (pH = 9), NH₃ (pH = 11), and NaOH (pH = 13). (b) pH paper contains a mixture of indicators that give different colours in solutions of differing pH values. (credit: modification of work by Sahar Atwa)

Questions

★ Questions

1. What is the relationship between [H⁺] and K_w? Write a mathematical expression that relates them.

2. Write the chemical equation for the autoionization of water and label the conjugate acid-base pairs.

3. If HNO₂ is ionized only to an extent of 0.445%, what are [H⁺] and [OH⁻] in a 0.307 M solution of HNO₂?

4. Explain why a sample of pure water at 40 °C is neutral even though [H₃O⁺] = 1.7 × 10−7 M. K_w is 2.9 × 10⁻¹⁴ at 40 °C.

5. The ionization constant for water (K_w) is 2.9 × 10⁻¹⁴ at 40 °C. Calculate [H₃O⁺], [OH⁻], pH, and pOH for pure water at 40 °C.

6. The ionization constant for water (K_w) is 9.311 × 10⁻¹⁴ at 60 °C. Calculate [H₃O⁺], [OH⁻], pH, and pOH for pure water at 60 °C.

7. Calculate the pH and the pOH of each of the following solutions at 25 °C for which the substances ionize completely:

(a) 0.200 M HCl

(b) 0.0143 M NaOH

(c) 3.0 M HNO₃

(d) 0.0031 M Ca(OH)₂

8.  Calculate the pH and the pOH of each of the following solutions at 25 °C for which the substances ionize completely:

(a) 0.000259 M HClO₄

(b) 0.21 M NaOH

(c) 0.000071 M Ba(OH)₂

(d) 2.5 M KOH

9. What are the pH and pOH of a solution of 2.0 M HCl, which ionizes completely?

10. What are the hydronium and hydroxide ion concentrations in a solution whose pH is 6.52?

11. Calculate the hydrogen ion concentration and the hydroxide ion concentration in wine from its pH. See Figure 5.2.2. for useful information.

12. Calculate the hydronium ion concentration and the hydroxide ion concentration in lime juice from its pH. See Figure 5.2.2. for useful information.

13. The hydronium ion concentration in a sample of rainwater is found to be 1.7 × 10⁻⁶ M at 25 °C. What is the concentration of hydroxide ions in the rainwater?

14. The hydroxide ion concentration in household ammonia is 3.2 × 10⁻³ M at 25 °C. What is the concentration of hydronium ions in the solution?

Answers

1. [H⁺] = K_w[OH⁻]

2. H₂O + H₂O → H₃O⁺ + OH⁻; H₂O/H₃O⁺ and H₂O/OH⁻

3. [H⁺] = 0.00137 M; [OH⁻] = 7.32 × 10⁻¹² M

4. In a neutral solution [H₃O⁺] = [OH⁻]. At 40 °C, [H₃O⁺] = [OH⁻] = (2.910−14)*(1/2) = 1.7 × 10⁻⁷ M

5. [H₃O⁺] = [OH⁻] = 1.703 x 10⁻⁷ M, pOH = pH = 6.77

6. x = 3.051 × 10⁻⁷ M = [H₃O⁺] = [OH⁻], pH = −log(3.051) × 10⁻⁷ = −(−6.5156) = 6.5156, pOH = pH = 6.5156

7. (a) pH = 0.699, pOH = 13.3, (b) pH = 12.15, pOH = 1.85, (c) pH = -0.477, pOH = 14.5, (d) pH = 12.8, pOH = 1.2

8. (a) pH = 3.587; pOH = 10.413; (b) pH = 0.68; pOH = 13.32; (c) pOH = 3.85; pH = 10.15; (d) pH = −0.40; pOH = 14.4

9. pOH = 14.301, pH = -0.301

10. [H₃O⁺]= 3.0 × 10⁻⁷ M; [OH⁻] = 3.3 × 10⁻⁸ M

11. [H₃O⁺]= 3.162 x 10⁻⁴ M; [OH⁻] = 3.162 x 10⁻¹¹ M

12. [H₃O⁺]= 1 × 10⁻² M; [OH⁻] = 1 × 10⁻¹² M

13. [OH^–] = 5.9 × 10^-9 M

14. [OH⁻] = 3.1 × 10−12 M