1.1 – The Mole
The Mole
The identity of a substance is defined by the type of atoms or ions it contains as well as the quantity of each type of atom or ion. For example, water, H2O, and hydrogen peroxide, H2O2, are alike in that their respective molecules are composed of hydrogen and oxygen atoms. However, because a hydrogen peroxide molecule contains two oxygen atoms, as opposed to the water molecule, which has only one, the two substances exhibit very different properties. Today, we possess sophisticated instruments that allow the direct measurement of these defining microscopic traits; however, the same traits were originally derived from the measurement of macroscopic properties (the masses and volumes of bulk quantities of matter) using relatively simple tools (balances and volumetric glassware). This experimental approach required the introduction of a new unit for the amount of substances, the mole, which remains indispensable in modern chemical science.
The mole is an amount unit similar to familiar units like pair, dozen, gross, etc. It provides a specific measure of the number of atoms or molecules in a bulk sample of matter. A mole is defined as the amount of substance containing the same number of discrete entities (such as atoms, molecules, and ions) as the number of atoms in a sample of pure 12C weighing exactly 12 g. To further illustrate this idea, 1 pair = 2 things, 1 dozen = 12 things, and 1 mole = 6.022 × 1023 things. One Latin connotation for the word “mole” is “large mass” or “bulk,” which is consistent with its use as the name for this unit. The mole provides a link between an easily measured macroscopic property, bulk mass, and an extremely important fundamental property, number of atoms, molecules, and so forth.
The number of entities composing a mole has been experimentally determined to be 6.02214179 × 1023, a fundamental constant named Avogadro’s number (NA) or the Avogadro constant in honour of Italian scientist Amedeo Avogadro. This constant is properly reported with an explicit unit of “per mole,” a conveniently rounded version being 6.022 × 1023mol-1.
Consistent with its definition as an amount unit, 1 mole of any element contains the same number of atoms as 1 mole of any other element. The masses of 1 mole of different elements, however, are different, since the masses of the individual atoms are drastically different. The molar mass of an element (or compound) is the mass in grams of 1 mole of that substance, a property expressed in units of grams per mole (g/mol) (see Figure 1.1.1).

Figure 1.1.1. Each sample contains 6.022 × 1023 atoms —1.00 mol of atoms. Top row (from left to right): 65.4 g zinc, 12.0 g carbon, 24.3 g magnesium, and 63.5 g copper. Bottom row (from left to right): 32.1 g sulfur, 28.1 g silicon, 207 g lead, and 118.7 g tin. (credit: modification of work by Mark Ott)
Because the definitions of both the mole and the atomic mass unit are based on the same reference substance, 12C, the molar mass of any substance is numerically equivalent to its atomic or formula weight in atomic mass units, or amu. Per the amu definition, a single 12C atom weighs 12 amu (its atomic mass is 12 amu). According to the definition of the mole, 12 g of 12C contains 1 mole of 12C atoms (its molar mass is 12 g/mol). This relationship holds for all elements since their atomic masses are measured relative to that of the amu-reference substance, 12C. Extending this principle, the molar mass of a compound in grams is likewise numerically equivalent to its formula mass in amu (Figure 1.1.2).

Figure 1.1.2. Each sample contains 6.02 × 1023 molecules or formula units—1.00 mol of the compound or element. Clock-wise from the upper left: 130.2 g of C8H17OH (1-octanol, formula mass 130.2 amu), 454.4 g of HgI2 (mercury(II) iodide, formula mass 454.4 amu), 32.0 g of CH3OH (methanol, formula mass 32.0 amu) and 256.5 g of S8 (sulfur, formula mass 256.5 amu). (credit: Sahar Atwa)
Table 1.1.1. Quantitative properties of selected elements.
| Element | Average Atomic Mass (amu) | Molar Mass (g/mol) | Atoms/Mole |
| C | 12.01 | 12.01 | 6.022 × 1023 |
| H | 1.008 | 1.008 | 6.022 × 1023 |
| O | 16.00 | 16.00 | 6.022 × 1023 |
| Na | 22.99 | 22.99 | 6.022 × 1023 |
| Cl | 35.45 | 33.45 | 6.022 × 1023 |
While atomic mass and molar mass are numerically equivalent, keep in mind that they are vastly different in terms of scale, as represented by the vast difference in the magnitudes of their respective units (amu versus g). To appreciate the enormity of the mole, consider a small drop of water weighing about 0.03 g (see Figure 1.1.3). Although this represents just a tiny fraction of 1 mole of water (~18 g), it contains more water molecules than can be clearly imagined. If the molecules were distributed equally among the roughly seven billion people on earth, each person would receive more than 100 billion molecules.

Figure 1.1.3. The number of molecules in a single droplet of water is roughly 100 billion times greater than the number of people on earth. (credit: “tanakawho”/Wikimedia commons)
The relationships between formula mass, the mole, and Avogadro’s number can be applied to compute various quantities that describe the composition of substances and compounds. These relationships can be summarized by the equations below, where n is the number of moles of substance, in units of moles; m is the mass of the substance, in units of grams; and MM is the molar mass of the substance, in units of g/mol. For example, if we know the mass and chemical composition of a substance, we can determine the number of moles and calculate the number of atoms or molecules in the sample. Likewise, if we know the number of moles of a substance, we can derive the number of atoms or molecules and calculate the substance’s mass.

Equation 1.1.1
Notice that these relationships can also be derived via Dimensional Analysis (also known as the factor-label method or unit analysis; an explanation of this process can be found in Appendix D).
Example 1.1.1 – Deriving Moles from Grams for an Element
According to nutritional guidelines from the US Department of Agriculture, the estimated daily average requirement for dietary potassium is 4.7 g. What is the estimated daily average requirement of potassium in moles?
Solution
The mass of K is provided, and the corresponding amount of K in moles is requested. Referring to the periodic table, the atomic mass of K is 39.10 amu, and so its molar mass is 39.10 g/mol. The given mass of K (4.7 g) is a bit more than one-tenth of the molar mass (39.10 g), so a reasonable “ballpark” estimate of the number of moles would be slightly greater than 0.1 mol.
According to Equation 1.1.1 (a), the molar amount of a substance may be calculated by dividing its mass (g) by its molar mass (g/mol):

Let’s confirm this mathematical approach by applying Dimensional Analysis, using the molar mass of potassium as a conversion factor to convert the number of grams of potassium to the number of moles of potassium. To do this, we multiply the mass by the reciprocal of the molar mass, and consequently the units of grams cancel out, leaving behind the desired unit, moles of potassium:
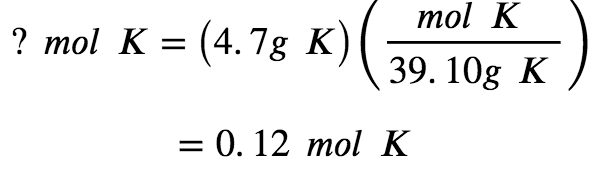
The calculated magnitude (0.12 mol K) is consistent with our ballpark expectation since it is a bit greater than 0.1 mol.
Check Your Learning 1.1.1 – Deriving Moles from Grams for an Element
Beryllium is a light metal used to fabricate transparent X-ray windows for medical imaging instruments. How many moles of Be are in a thin-foil window weighing 3.24 g?
Answer
n = 0.360 mol
Example 1.1.2 – Deriving Grams from Moles for an Element
A litre of air contains 9.2 × 10−4 mol argon. What is the mass of Ar in a litre of air?
Solution
The molar amount of Ar is provided and must be used to derive the corresponding mass in grams. Since the amount of Ar is less than 1 mole, the mass will be less than the mass of 1 mole of Ar, approximately 40 g. The molar amount in question is approximately one-one thousandth (~10−3) of a mole, and so the corresponding mass should be roughly one-one thousandth of the molar mass (~0.04 g):

In this case, we can rearrange Equation 1.1.1 (a), multiplying the provided amount (in mol) by the molar mass (in g/mol) to find the mass, in grams. This approach is also supported by Dimensional Analysis: 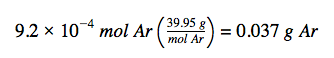
The result is in agreement with our expectations, around 0.04 g Ar.
Check Your Learning 1.1.2 – Deriving Grams from Moles for an Element
What is the mass of 2.561 mol of gold?
Answer
m = 504.4 g
Example 1.1.3 – Deriving Number of Atoms from Mass for an Element
Copper is commonly used to fabricate electrical wire (Figure 1.1.4.). How many copper atoms are in 5.00 g of copper wire?

Figure 1.1.4. Copper wire is composed of many, many atoms of Cu. (credit: Emilian Robert Vicol)
Solution
The number of Cu atoms in the wire may be conveniently derived from its mass by a two-step computation: first calculating the molar amount of Cu, and then using Avogadro’s number (NA) to convert this molar amount to the number of Cu atoms:

Considering that the provided sample mass (5.00 g) is a little less than one-tenth of the mass of 1 mole of Cu (~64 g), a reasonable estimate for the number of atoms in the sample would be on the order of one-tenth NA, or approximately 1022 Cu atoms. Carrying out the two-step computation yields: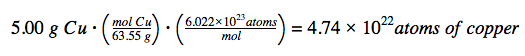
Dimensional Analysis yields the desired cancellation of units, and the computed result is on the order of 1022 as expected.
Check Your Learning 1.1.3 – Deriving Number of Atoms from Mass for an Element
A prospector panning for gold in a river collects 15.00 g of pure gold. How many Au atoms are in this quantity of gold?
Answer
4.586 × 1022 Au atoms
Example 1.1.4 – Deriving Moles from Grams for a Compound
Our bodies synthesize protein from amino acids. One of these amino acids is glycine, which has the molecular formula C2H5O2N. How many moles of glycine molecules are contained in 28.35 g of glycine?
Solution
We can derive the number of moles of a compound from its mass following the same procedure we used for an element:
The molar mass of glycine is required for this calculation, and it is computed in the same fashion as its molecular mass. One mole of glycine, C2H5O2N, contains 2 moles of carbon, 5 moles of hydrogen, 2 moles of oxygen, and 1 mole of nitrogen:
| Element | Quantity (mol element / mol compound) | Molar Mass (g / mol element) | Subtotal (g / mol compound) |
| C | 2 | x 12.01 | = 24.02 |
| H | 5 | x 1.008 | = 5.040 |
| O | 2 | x 16.00 | = 32.00 |
| N | 1 | x 14.01 | = 14.01 |
| Molar mass (g / mol compound) | 75.07 |
The provided mass of glycine (~28 g) is a bit more than one-third of the molar mass (~75 g/mol), so we would expect the computed result to be a bit greater than one-third of a mole (~0.33 mol). Dividing the compound’s mass by its molar mass yields: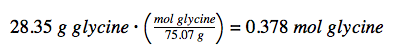 This result is consistent with our rough estimate.
This result is consistent with our rough estimate.
Check Your Learning 1.1.4 – Deriving Moles from Grams for a Compound
How many moles of sucrose, C12H22O11, are in a 25-g sample of sucrose?
Answer
n = 0.073 mol
Example 1.1.5 – Deriving Grams from Moles for a Compound
Vitamin C is a covalent compound with the molecular formula C6H8O6. The recommended daily dietary allowance of vitamin C for children aged 4–8 years is 1.42 × 10−4 mol. What is the mass of this allowance in grams?
Solution
As for elements, the mass of a compound can be derived from its molar amount as shown:

The molar mass for this compound is computed to be 176.124 g/mol. The given number of moles is a very small fraction of a mole (~10−4 or one-ten thousandth); therefore, we would expect the corresponding mass to be about one-ten thousandth of the molar mass (~0.02 g). Performing the calculation, we get:
![]()
This is consistent with the anticipated result.
Check Your Learning 1.1.5 – Deriving Grams from Moles for a Compound
What is the mass of 0.443 mol of hydrazine, N2H4?
Answer
m = 14.2 g
Example 1.1.6 – Deriving the Number of Atoms and Molecules from the Mass of a
Compound
A packet of an artificial sweetener contains 40.0 mg of saccharin (C7H5NO3S), which has the structural formula: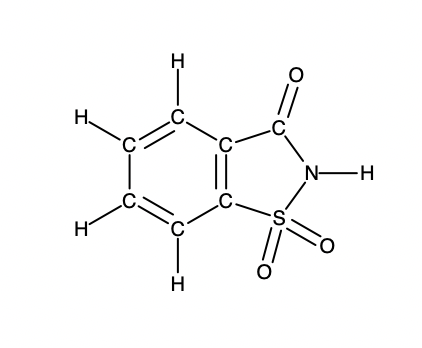
Given that saccharin has a molar mass of 183.18 g/mol, how many saccharin molecules are in a 40.0 mg (0.0400 g) sample of saccharin? How many carbon atoms are in the same sample?
Solution
The number of molecules in a given mass of a compound is computed by first deriving the number of moles, and then multiplying by Avogadro’s number:

Using the provided mass and molar mass for saccharin yields:
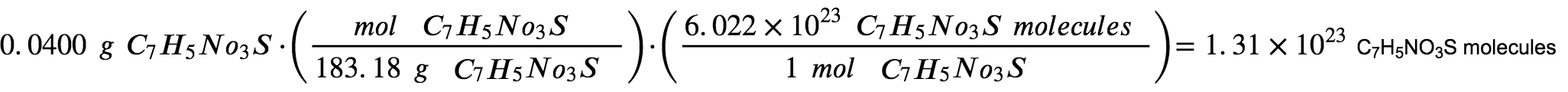
The compound’s formula shows that each molecule contains seven carbon atoms, and so the number of C atoms in the provided sample is:
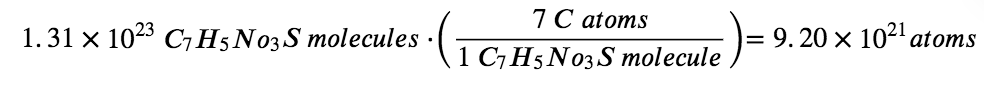
Check Your Learning 1.1.6 – Deriving the Number of Atoms and Molecules from the Mass of a Compound
How many C4H10 molecules are contained in 9.213 g of this compound? How many hydrogen atoms?
Answer
9.545 × 1022 molecules C4H10; 9.545 × 1023 atoms H
Percent Composition
The elemental makeup of a compound defines its chemical identity, and chemical formulas are the most succinct way of representing this elemental makeup. When a compound’s formula is unknown, measuring the mass of each of its constituent elements is often the first step in the process of determining the formula experimentally. The results of these measurements permit the calculation of the compound’s percent composition, defined as the percentage by mass of each element in the compound. For example, consider a gaseous compound composed solely of carbon and hydrogen. The percent composition of this compound could be represented as follows:
![]()
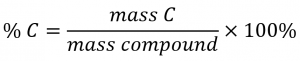
If the analysis of a 10.0 g sample of this gas showed it to contain 2.5 g H and 7.5 g C, the percent composition would be calculated to be 25% H and 75% C:
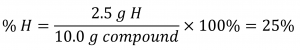
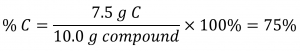
A chemical compound is the combination of two or more elements. If you are studying a chemical compound, you may want to find the percent composition of a certain element within that chemical compound. The general equation for percent composition is:
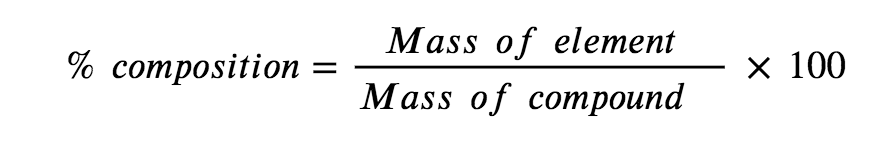
Equation 1.1.1. Percent composition.
If you want to know the percent composition of the elements in a compound, follow these steps:
Steps to Solve:
1. Find the molar mass of all the elements in the compound in grams per mole.
2. Find the mol1) mass of the entire compound.
3. Divide the component’s molar mass by the entire molecular mass.
4. You will now have a number between 0 and 1. Multiply it by 100 to get percent composition!
Tips for solving:
The compounds will always add up to 100%, so in a binary compound, you can find the percent of the first element, then subtract from 100% to determine the percent of the second element.
If using a calculator, you can store the overall molar mass to a variable such as “A”. This will speed up calculations, and reduce typographical errors.
These steps are outlined in Example 1.1.7.
Example 1.1.7 – Percent Composition
Find the percent composition of phosphorus pentachloride (PCl5).
Solution
1) Assume you have exactly one mole of phosphorus pentachloride. Using the molecular formula and the molar mass of each element, find the mass of each element present:
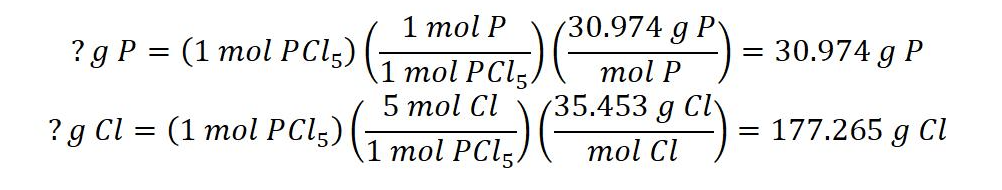
2) Find the molecular mass:
PCl5 = 30.974 g + 177.265 g = 208.239 g
3) Divide each molar mass by the molecular mass and multiply by 100:
![]()
![]()
Therefore, phosphorus pentachloride is 14.87% P and 85.13% Cl by mass.
Check Your Learning 1.1.7 – Percent Composition
Find the percent composition of hydrochloric acid (HCl).
Answer
HCl is 2.76 % hydrogen and 97.24 % chlorine by mass.
★ Questions
1. Compare 1 mole of H2, 1 mole of O2, and 1 mole of F2. Which has the largest number of molecules? Explain why.
2. Which contains the greatest mass of oxygen: 0.75 mol of ethanol (C2H5OH), 0.60 mol of formic acid (HCO2H), or 1.0 mol of water (H2O)? Explain why.
3. How are the molecular mass and the molar mass of a compound similar and how are they different?
4. Calculate the molar mass (in g/mol) of each of the following:
(a) The anesthetic halothane, C2HBrClF3
(b) The herbicide paraquat, C12H14N2Cl2
(c) Caffeine, C8H10N4O2
(d) Urea, CO(NH2)2
(e) A typical soap, C17H35CO2Na
5. Determine the number of moles of the compound and the number of moles (in mol) of each type of atom in each of the following:
(a) 25.0 g of propylene, C3H6
(b) 3.06 x10-3 g of the amino acid glycine, C2H5NO2
(c) 25 lb of the herbicide Treflan, C13H16N2O4F (1 lb = 454 g)
(d) 0.125 kg of the insecticide Paris Green, Cu4(AsO3)2(CH3CO2)2
(e) 325 mg of aspirin, C6H4(CO2H)(CO2CH3)
6. Determine the mass (in grams) of each of the following:
(a) 0.0146 mol KOH
(b) 10.2 mol ethane, C2H6
(c) 1.6 x 10-3 mol Na2SO4
(d) 6.854 x 103 mol glucose, C6H12O6
(e) 2.86 mol Co(NH3)6Cl3
★★ Questions
7. One 55-gram serving of a particular cereal supplies 270 mg of sodium, 11% of the recommended daily allowance. How many moles and atoms of sodium are in the recommended daily allowance?
8. A certain nut crunch cereal contains 11.0 grams of sugar (sucrose, C12H22O11) per serving size of 60.0 grams. How many servings of this cereal must be eaten to consume 0.0278 moles of sugar?
9. Which of the following represents the least number of molecules?
(a) 20.0 g of H2O (18.02 g/mol)
(b) 77.0 g of CH4 (16.06 g/mol)
(c) 68.0 g of CaH2 (42.09 g/mol)
(d) 100.0 g of N2O (44.02 g/mol)
(e) 84.0 g of HF (20.01 g/mol)
Answers
1. Since there is 1 mole of each, they all have the same number of molecules.
2. Formic acid. Its formula has twice as many oxygen atoms as the other two compounds (one each). Therefore, 0.60 mol of formic acid would be equivalent to 1.20 mol of a compound containing a single oxygen atom.
3. The two masses have the same numerical value, but the units are different: The molecular mass is the mass of 1 molecule while the molar mass is the mass of 6.022 × 1023 molecules.
4. (a) 197.382 g/mol; (b) 257.163 g/mol; (c) 194.193 g/mol; (d) 60.056 g/mol; (e) 306.464 g/mol
5. (a) 0.594 mol C3H6, 1.78 mol C, 3.56 mol H; (b) 4.08 × 10-5 mol C2H5NO2, 8.15 × 10-5 mol C, 2.04 × 10-4 mol H, 4.08 × 10-5 mol N, 8.15 × 10-5 mol O; (c) 40.06 mol C13H16N2O4F, 520.79 mol C, 640.98 mol H, 80.12 mol N, 160.24 mol O, 40.06 mol F; (d) 0.202 mol Cu4(AsO3)2(CH3CO2)2, 0.81 mol Cu, 0.40 mol As, 2.02 mol O, 0.81 mol C, 1.21 mol H; (e) 1.80 × 10-3 mol C6H4(CO2H)(CO2CH3), 0.016 mol C, 0.014 H, 7.22 × 10-3 mol O
6. (a) 0.819 g; (b) 307 g; (c) 0.23 g; (d) 1.235 × 106 g (1235 kg); (e) 765 g
7. 0.107 mol Na, 6.43 × 1022 atoms Na
8. 0.865 servings, or about 1 serving.
9. (a) 20.0 g H2O represents the least number of molecules since it has the least number of moles.
Amount of substance containing the same number of atoms, molecules, ions, or other entities as the number of atoms in exactly 12 grams of 12C; equals 6.022e^23 things
The experimentally determined value of the number of entities comprising 1 mole of substance, equal to 6.022E23 molE-1
Mass in grams of 1 mole of a substance
Percentage by mass of the various elements in a compound

