7.3 – Rate Laws

As described in the previous section, the rate of a reaction is affected by the concentrations of reactants. Rate laws or rate equations are mathematical expressions that describe the relationship between the rate of a chemical reaction and the concentration of its reactants. In general, a rate law (or differential rate law, as it is sometimes called) takes this form:

in which [A], [B], and [C] represent the molar concentrations of reactants, and k is the rate constant, which is specific for a particular reaction at a particular temperature. The numerical value of the rate constant is specific for a particular reaction under a given set of conditions, including temperature, pressure, reactant phase, solvents, etc. We will see later how individual factors influence the numeric value of k. Note that the numeric value of the rate constant is independent of the concentrations of the reactants A, B, or C, but we will see in the next section how the units of k are affected by the exponents m, n, and p. The numerical value of k, however, does not change as the reaction progresses under a given set of conditions. The exponents m, n, and p are usually positive integers (although it is possible for them to be fractions or negative numbers). The rate constant k and the exponents m, n, and p must be determined experimentally by observing how the rate of a reaction changes as the concentrations of the reactants are changed. The exponents in a rate law describe the effects of the reactant concentrations on the reaction rate and define the reaction order. Consider a reaction for which the rate law is:

If the exponent m is 1, the reaction is first order with respect to A. If m is 2, the reaction is second order with respect to A. If n is 1, the reaction is first order in B. If n is 2, the reaction is second order in B. If m or n is zero, the reaction is zero order in A or B, respectively, and the rate of the reaction is not affected by the concentration of that reactant. The overall reaction order is the sum of the orders with respect to each reactant. If m = 1 and n = 1, the overall order of the reaction is second-order (m + n = 1 + 1 = 2).

The rate law:

describes a reaction that is first order in hydrogen peroxide and first order overall. The rate law:

describes a reaction that is second order in C₄H₆ and second-order overall. The rate law:

describes a reaction that is first order in H⁺, first-order in OH⁻, and second-order overall.

Reaction Order and Rate Constant Units

Sometimes, the reaction orders in the rate law happen to be the same as the coefficients in the chemical equation for the reaction. This is merely a coincidence and very often not the case.

Rate laws may exhibit fractional orders for some reactants, and negative reaction orders are sometimes observed when an increase in the concentration of one reactant causes a decrease in reaction rate. A few examples illustrating these points are provided:

2N2O5 (g)  →  4NO2 (g) + O2(g)	Rate = k[N2O5]
2NO2 (g) + F2(g)  →  2NO2F (g)	Rate = k[NO2][F2]
2H2O2(aq)  →  2H2O (l) + O2(g)	Rate = k[H2O2]
H2 (g) + Br2 (g)  →  2HBr (g)	Rate = k[H2][Br2]
O3 (g) + CI (g)  →  O2 (g) + CIO (g)	Rate = k[O3][CI]

It is important to note that rate laws are determined by experiment only and are not reliably predicted by reaction stoichiometry.

Reaction orders also play a role in determining the units for the rate constant k. For example, in a second-order reaction, the units for k are L mol⁻¹ s⁻¹, whereas in a third-order reaction, the units for k are mol⁻² L²/s. This is because the rate must always be in the form of M/s or mol/L•s, hence the units of individual concentrations must work out to one of the aforementioned units. More generally speaking, the units for the rate constant for a reaction of order (m + n) are mol^1−(m+n) L^(m+n)−1 s⁻¹. The table below summarizes the rate constant units for common reaction orders.

Table 7.3.1 Rate Constants for Common Reaction Orders

Note that the units in the table can also be expressed in terms of molarity (M) instead of mol/L. Also, units of time other than the second (such as minutes, hours, days) may be used, depending on the situation.

Example 7.3.1 – Writing Rate Laws from Reaction Orders

An experiment shows that the reaction of nitrogen dioxide with carbon monoxide:

is second order in NO₂ and zero-order in CO at 100°C. What is the rate law for the reaction? What are the units of k?

Solution

The reaction will have the form:

The reaction is second order in NO₂; thus m = 2. The reaction is zero order in CO; thus n = 0. The rate law is:

From this we know that the rate must be in M/s and the concentration (once squared) will be in M², hence our k value must be M^-1s^-1.

Remember that a number raised to the zero power is equal to 1, thus [CO]⁰ = 1, which is why we can simply drop the concentration of CO from the rate equation: the rate of reaction is solely dependent on the concentration of NO₂. When we consider rate mechanisms later in this chapter, we will explain how a reactant’s concentration can have no effect on a reaction despite being involved in the reaction.

Check Your Learning 7.3.1 – Writing Rate Laws from Reaction Orders

The rate law for the reaction:

has been determined to be rate = k[NO]²[H₂]. What are the orders with respect to each reactant, and what is the overall order of the reaction?

Answer

order in NO = 2; order in H₂ = 1; overall order = 3

Check Your Learning 7.3.2 – Writing Rate Laws from Reaction Orders

In a transesterification reaction, a triglyceride reacts with an alcohol to form an ester and glycerol. Many students learn about the reaction between methanol (CH₃OH) and ethyl acetate (CH₃CH₂OCOCH₃) as a sample reaction before studying the chemical reactions that produce biodiesel:

The rate law for the reaction between methanol and ethyl acetate is, under certain conditions, determined to be:

What is the order of reaction with respect to methanol and ethyl acetate, and what is the overall order of reaction?

Answer

order in CH₃OH = 1; order in CH₃CH₂OCOCH₃ = 0; overall order = 1

Example 7.3.2 – Interpreting Rate Laws

Below are three reactions and their experimentally determined differential rate laws. For each reaction, give the units of the rate constant, give the reaction order with respect to each reactant, give the overall reaction order, and predict what happens to the reaction rate when the concentration of the first species in each chemical equation is doubled.

Solution

(a) [HI]² will give units of (moles per litre)². For the reaction rate to have units of moles per litre per second, the rate constant must have reciprocal units [1/(M·s)]:

The exponent in the rate law is 2, so the reaction is second order in HI. Because HI is the only reactant and the only species that appears in the rate law, the reaction is also second-order overall.

If the concentration of HI is doubled, the reaction rate will increase from k[HI]₀² to k(2[HI])₀² = 4k[HI]₀². The reaction rate will therefore quadruple.

(b) Because no concentration term appears in the rate law, the rate constant must have M/s units for the reaction rate to have M/s units.
The rate law tells us that the reaction rate is constant and independent of the N₂O concentration. That is, the reaction is zeroth order in N₂O and zeroth-order overall.

Because the reaction rate is independent of the N₂O concentration, doubling the concentration will have no effect on the reaction rate.

(c) The rate law contains only one concentration term raised to the first power. Hence the rate constant must have units of reciprocal seconds (s⁻¹) to have units of moles per litre per second for the reaction rate: M·s⁻¹ = M/s.

The only concentration in the rate law is that of cyclopropane, and its exponent is 1. This means that the reaction is first order in cyclopropane. Cyclopropane is the only species that appears in the rate law, so the reaction is also first-order overall.

Doubling the initial cyclopropane concentration will increase the reaction rate from k[cyclopropane]₀ to 2k[cyclopropane]₀. This doubles the reaction rate.

Check Your Learning 7.3.3 – Interpreting Rate Laws

Given the following two reactions and their experimentally determined differential rate laws: determine the units of the rate constant if time is in seconds, determine the reaction order with respect to each reactant, give the overall reaction order, and predict what will happen to the reaction rate when the concentration of the first species in each equation is doubled.

with

with

Answer

(a) s⁻¹; first order in CH₃N=NCH₃; first-order overall; doubling [CH₃N=NCH₃] will double the reaction rate.

(b) M⁻¹·s⁻¹; first order in NO₂, first-order in F₂; second-order overall; doubling [NO₂] will double the reaction rate.

Experimental Kinetics – Method of Initial Rates

The number of fundamentally different mechanisms (sets of steps in a reaction) is actually rather small compared to the large number of chemical reactions that can occur. Thus understanding reaction mechanisms can simplify what might seem to be a confusing variety of chemical reactions. The first step in discovering the reaction mechanism is to determine the reaction’s rate law. This can be done by designing experiments that measure the concentration(s) of one or more reactants or products as a function of time.

For the reaction A + B → products, for example, we need to determine k and the exponents m and n in the following equation:

Equation 7.3.1 Rate Law Equation

We can use an explicit algebraic method, often referred to as the method of initial rates, to determine the orders in rate laws. To use this method, we select two sets of rate data that differ in the concentration of only one reactant and set up a ratio of the two rates and the two rate laws. After cancelling terms that are equal, we are left with an equation that contains only one unknown, the coefficient of the concentration that varies. We then solve this equation for the coefficient. Rate data for a hypothetical reaction of the type A + B → products are given in the table below.

Table 7.3.2 Initial Rate to Concentration

The general rate law for the reaction is

Equation 7.3.2 General Rate Law

We can obtain m or n directly by using a proportion of the rate laws for two experiments in which the concentration of one reactant is the same, such as Experiments 1 and 3 in the table above.

Inserting the appropriate values from the table,

Because 1.00 to any power is 1, [1.00 M]^m = 1.00 M. We can cancel like terms to give 0.25 = [0.50]^m, which can also be written as 1/4 = [1/2]^m. Thus we can conclude that m = 2 and that the reaction is second order in A. By selecting two experiments in which the concentration of B is the same, we were able to solve for m.

Conversely, by selecting two experiments in which the concentration of A is the same (e.g., Experiments 5 and 1), we can solve for n.

 

Substituting the appropriate values from the table,

Canceling leaves 1.0 = [0.50]ⁿ, which gives n = 0; that is, the reaction is zeroth-order in B. The experimentally determined rate law is therefore

rate = k[A]²[B]⁰ = k[A]²

We can now calculate the rate constant by inserting the data from any row of the table into the experimentally determined rate law and solving for k. Using Experiment 2, we obtain

19 × 10⁻³ M/min = k(0.75 M)²

3.4 × 10⁻² M⁻¹·min⁻¹ = k

You should verify that using data from any other row of the table gives the same rate constant. This must be true as long as the experimental conditions, such as temperature and solvent, are the same.

Example 7.3.3 – Determining a Rate Law from Initial Rates – 1

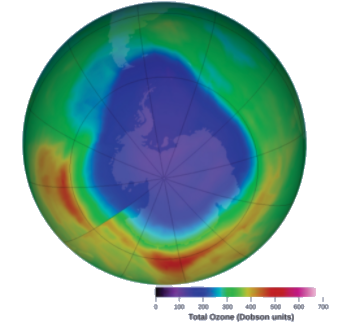
Ozone in the upper atmosphere is depleted when it reacts with nitrogen oxides. The rates of the reactions of nitrogen oxides with ozone are important factors in deciding how significant these reactions are in the formation of the ozone hole over Antarctica (Figure 7.3.7). One such reaction is the combination of nitric oxide, NO, with ozone, O₃:

Figure 7.3.1. Over the past several years, the atmospheric ozone concentration over Antarctica has decreased during the winter. This map shows the decreased concentration as a purple area.

 

This reaction has been studied in the laboratory, and the following rate data were determined at 25°C.

Determine the rate law and the rate constant for the reaction at 25°C.

Solution

The rate law will have the form:

We can determine the values of m, n, and k from the experimental data using the following three-part process:

1. Determine the value of m from the data in which [NO] varies and [O₃] is constant. In the last three experiments, [NO] varies while [O₃] remains constant. When [NO] doubles from trial 3 to 4, the rate doubles, and when [NO] triples from trial 3 to 5, the rate also triples. Thus, the rate is also directly proportional to [NO], and m in the rate law is equal to 1.

2. Determine the value of n from data in which [O₃] varies and [NO] is constant. In the first three experiments, [NO] is constant and [O₃] varies. The reaction rate changes in direct proportion to the change in [O₃]. When [O₃] doubles from trial 1 to 2, the rate doubles; when [O₃] triples from trial 1 to 3, the rate increases also triples. Thus, the rate is directly proportional to [O₃], and n is equal to 1.The rate law is thus:

3. Determine the value of k from one set of concentrations and the corresponding rate.

The large value of k tells us that this is a fast reaction that could play an important role in ozone depletion if [NO] is large enough.

Check Your Learning 7.3.4 – Determining a Rate Law from Initial Rates – 1

Acetaldehyde decomposes when heated to yield methane and carbon monoxide according to the equation:

CH₃CHO (g)  →  CH₄ (g) + CO (g)

Determine the rate law and the rate constant for the reaction from the following experimental data:

Answer

rate = k[CH₃CHO]² with k = 6.73 × 10⁻⁶ L/mol/s

Example 7.3.4 – Determining a Rate Law from Initial Rates – 2

Nitric oxide is produced in the body by several different enzymes and acts as a signal that controls blood pressure, long-term memory, and other critical functions. The major route for removing NO from biological fluids is via reaction with O₂ to give NO₂, which then reacts rapidly with water to give nitrous acid and nitric acid:

2NO + O₂  →  2NO₂

These reactions are important in maintaining steady levels of NO. The following table lists kinetics data for the reaction of NO with O₂ at 25°C:

2NO (g) + O₂ (g) → 2NO₂ (g)

Determine the rate law for the reaction and calculate the rate constant.

Solution

Comparing Experiments 1 and 2 shows that as [O₂] is doubled at a constant value of [NO₂], the reaction rate approximately doubles. Thus the reaction rate is proportional to [O₂]¹, so the reaction is first order in O₂. Comparing Experiments 1 and 3 shows that the reaction rate essentially quadruples when [NO] is doubled and [O₂] is held constant. That is, the reaction rate is proportional to [NO]², which indicates that the reaction is second order in NO. Using these relationships, we can write the rate law for the reaction:

rate = k[NO]²[O₂]. The data in any row can be used to calculate the rate constant. Using Experiment 1, for example, gives

Alternatively, using Experiment 2 gives

The difference is minor and associated with significant digits and likely experimental error in making the table.

The overall reaction order (m + n) = 3, so this is a third-order reaction whose rate is determined by three reactants. The units of the rate constant become more complex as the overall reaction order increases.

Check Your Learning 7.3.5 – Determining a Rate Law from Initial Rates – 2

The peroxydisulfate ion (S₂O₈²⁻) is a potent oxidizing agent that reacts rapidly with iodide ion in water:

S₂O₈^2- (aq) + 3I^1- (aq) → 2SO₄^2- (aq) + I₃^– (aq)

The following table lists kinetics data for this reaction at 25°C. Determine the rate law and calculate the rate constant.

Answer

rate = k[S₂O₈²⁻][I⁻]; k = 20 M⁻¹·s⁻¹

Integrated Rate Laws

The rate laws we have seen thus far relate the rate and the concentrations of reactants. We can also determine a second form of each rate law that relates the concentrations of reactants and time. These are called integrated rate laws. We can use an integrated rate law to determine the amount of reactant or product present after a period of time or to estimate the time required for a reaction to proceed to a certain extent. For example, an integrated rate law is used to determine the length of time a radioactive material must be stored for its radioactivity to decay to a safe level.

Using calculus, the differential rate law for a chemical reaction can be integrated with respect to time to give an equation that relates the amount of reactant or product present in a reaction mixture to the elapsed time of the reaction. This process can either be very straightforward or very complex, depending on the complexity of the differential rate law. For purposes of discussion, we will focus on the resulting integrated rate laws for zero-, first-, second-order reactions.

In addition, we’ll be looking at the case of half-life for these reactions of different orders. The half-life of a reaction (t_1/2) is the time required for one-half of a given amount of reactant to be consumed. In each succeeding half-life, half of the remaining concentration of the reactant is consumed. Using the decomposition of hydrogen peroxide as an example, we find that during the first half-life (from 0.00 hours to 6.00 hours), the concentration of H₂O₂ decreases from 1.000 M to 0.500 M. During the second half-life (from 6.00 hours to 12.00 hours), it decreases from 0.500 M to 0.250 M; during the third half-life, it decreases from 0.250 M to 0.125 M. The concentration of H₂O₂ decreases by half during each successive period of 6.00 hours. The decomposition of hydrogen peroxide is a first-order reaction, and, as can be shown, the half-life of a first-order reaction is independent of the concentration of the reactant. However, half-lives of reactions with other orders depend on the concentrations of the reactants.

Zero-Order Reactions

For zero-order reactions, the differential rate law is:

Rate = k[A]⁰ = k

Equation 7.3.3 Zero Order Differential Rate Law

A zero-order reaction thus exhibits a constant reaction rate, regardless of the concentration of its reactants.

[A] = -kt + [A]₀

y = mx + b

Because rate is independent of reactant concentration, a graph of the concentration of any reactant as a function of time is a straight line with a slope of −k. The value of k is negative because the concentration of the reactant decreases with time. Conversely, a graph of the concentration of any product as a function of time is a straight line with a slope of k, a positive value.

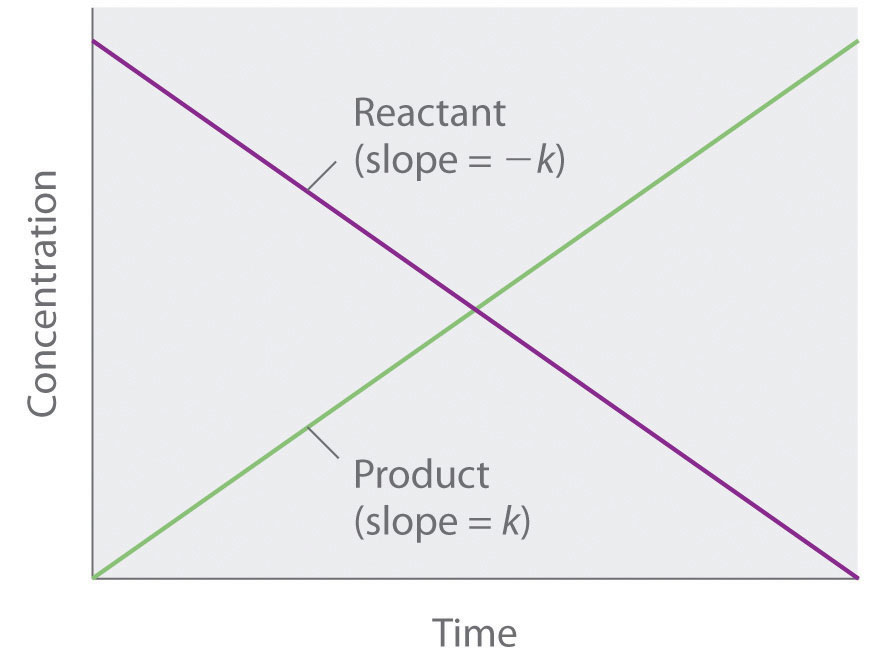
Figure 7.3.2. The graph of a zeroth-order reaction. The change in concentration of reactant and product with time produces a straight line.

The integrated rate law for a zeroth-order reaction also produces a straight line and has the general form

[A] = [A]₀ – kt

where [A]₀ is the initial concentration of reactant A. The equation above has the form of the algebraic equation for a straight line, y = mx + b, with y = [A], mx = −kt, and b = [A]₀.) In a zeroth-order reaction, the rate constant must have the same units as the reaction rate, typically moles per litre per second.

Although it may seem counterintuitive for the reaction rate to be independent of the reactant concentration(s), such reactions are rather common. They occur most often when the reaction rate is determined by available surface area. An example is the decomposition of N₂O on a platinum (Pt) surface to produce N₂ and O₂, which occurs at temperatures ranging from 200°C to 400°C:

2N₂O (g)

Without a platinum surface, the reaction requires temperatures greater than 700°C, but between 200°C and 400°C, the only factor that determines how rapidly N₂O decomposes is the amount of Pt surface available (not the amount of Pt). As long as there is enough N₂O to react with the entire Pt surface, doubling or quadrupling the N₂O concentration will have no effect on the reaction rate. At very low concentrations of N₂O, where there are not enough molecules present to occupy the entire available Pt surface, the reaction rate is dependent on the N₂O concentration. The reaction rate is as follows:

Thus the rate at which N₂O is consumed and the rates at which N₂ and O₂ are produced are independent of concentration. As shown in Figure 7.3.3 below, the change in the concentrations of all species with time is linear. Most important, the exponent (0) corresponding to the N₂O concentration in the experimentally derived rate law is not the same as the reactant’s stoichiometric coefficient in the balanced chemical equation (2). For this reaction, as for all others, the rate law must be determined experimentally.

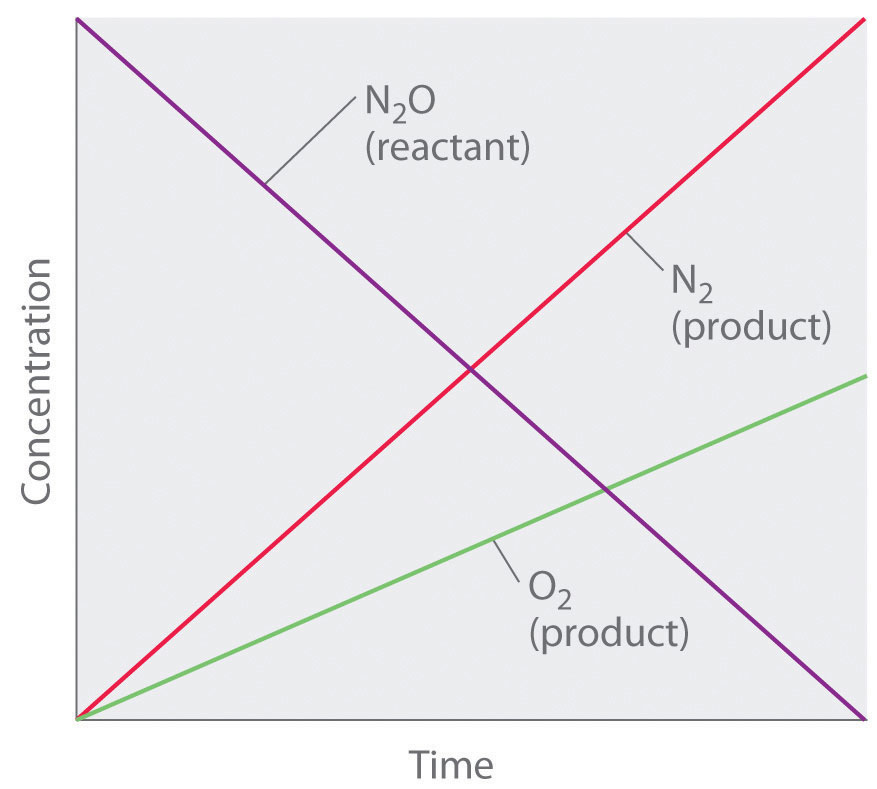
Figure 7.3.3. This graph shows the concentrations of reactants and products versus time for the zeroth-order catalyzed decomposition of N₂O to N₂ and O₂ on a Pt surface. The change in the concentrations of all species with time is linear.

A zeroth-order reaction that takes place in the human liver is the oxidation of ethanol (from alcoholic beverages) to acetaldehyde, catalyzed by the enzyme alcohol dehydrogenase. At high ethanol concentrations, this reaction is also a zeroth-order reaction. The overall reaction equation is

CH₃CH₂OH + NAD⁺

where NAD⁺ (nicotinamide adenine dinucleotide) and NADH (reduced nicotinamide adenine dinucleotide) are the oxidized and reduced forms, respectively, of a species used by all organisms to transport electrons. When an alcoholic beverage is consumed, the ethanol is rapidly absorbed into the blood. Its concentration then decreases at a constant rate until it reaches zero (part (a) in Figure 7.3.4). An average 70 kg person typically takes about 2.5 h to oxidize the 15 mL of ethanol contained in a single 12 oz can of beer, a 5 oz glass of wine, or a shot of distilled spirits (such as whiskey or brandy). The actual rate, however, varies a great deal from person to person, depending on body size and the amount of alcohol dehydrogenase in the liver. The reaction rate does not increase if a greater quantity of alcohol is consumed over the same period of time because the reaction rate is determined only by the amount of enzyme present in the liver. Contrary to popular belief, the caffeine in coffee is ineffective at catalyzing the oxidation of ethanol. When the ethanol has been completely oxidized and its concentration drops to essentially zero, the rate of oxidation also drops rapidly (part (b) in Figure 7.3.4).

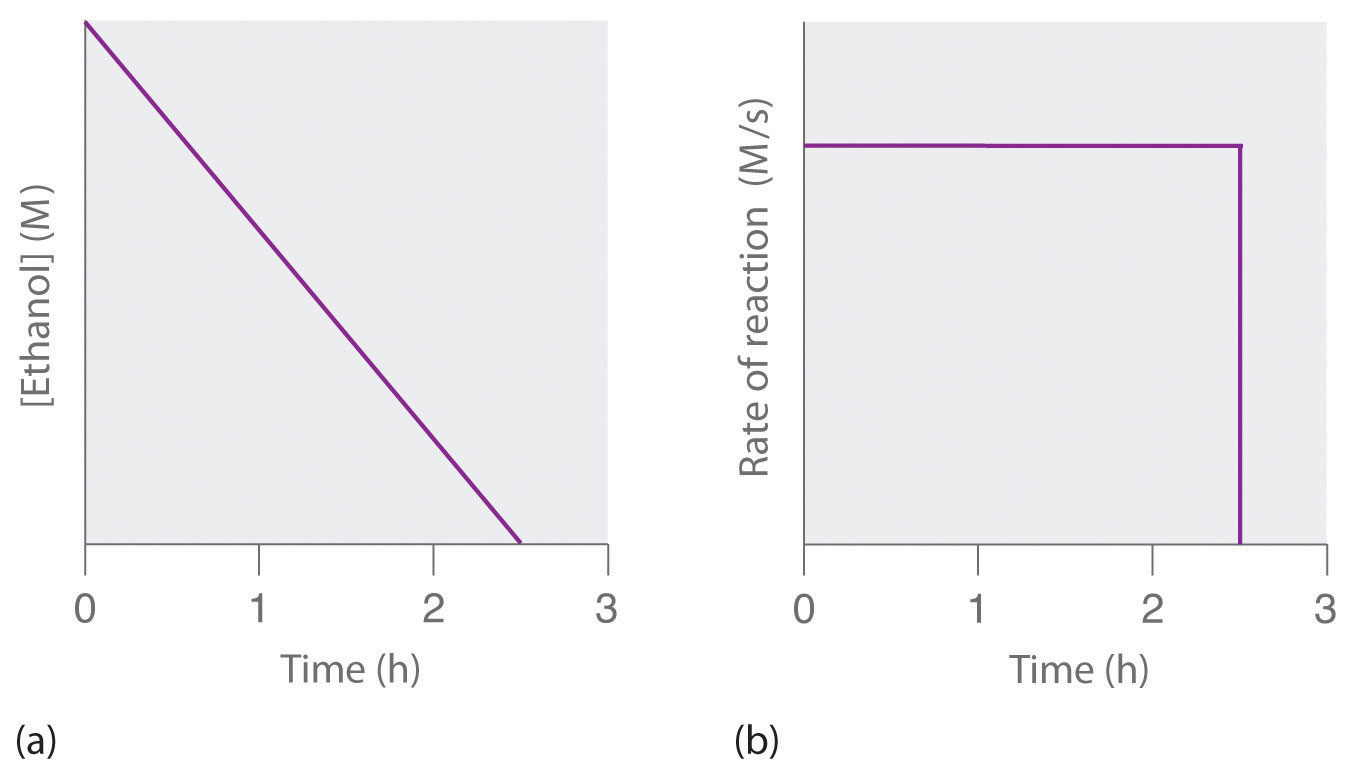
Figure 7.3.4. The Catalyzed Oxidation of Ethanol​ (a) The concentration of ethanol in human blood decreases linearly with time, which is typical of a zeroth-order reaction. (b) The rate at which ethanol is oxidized is constant until the ethanol concentration reaches essentially zero, at which point the reaction rate drops to zero.

These examples illustrate two important points:

In a zeroth-order reaction, the reaction rate does not depend on the reactant concentration.

A linear change in concentration with time is a clear indication of a zeroth-order reaction.

Half-Life of Zero-Order Reactions

We can derive an equation for calculating the half-life of a zero-order reaction as follows:

[A] = -kt + [A]₀

When half of the initial amount of reactant has been consumed t = t_1/2 and [A] = [A]₀²

Thus:

kt_1/2 = [A]₀ – [A]₀² = [A]₀²

and

t_1/2 = [A]₀²k

The half-life of a zero-order reaction increases as the initial concentration increases; hence, its half-life is dependent on the concentration.

First-Order Reactions

In a first-order reaction, the reaction rate is directly proportional to the concentration of one of the reactants. First-order reactions often have the general form A → products. The differential rate for a first-order reaction is as follows:

If the concentration of A is doubled, the reaction rate doubles; if the concentration of A is increased by a factor of 10, the reaction rate increases by a factor of 10, and so forth. Because the units of the reaction rate are always moles per litre per second, the units of a first-order rate constant are reciprocal seconds (s⁻¹).

The integrated rate law for a first-order reaction can be written in two different ways: one using exponents and one using logarithms. The exponential form is as follows:

[A] = [A]₀e^-kt

where [A]₀ is the initial concentration of reactant A at t = 0; k is the rate constant; and e is the base of the natural logarithms, which has the value 2.718 to three decimal places. Recall that an integrated rate law gives the relationship between reactant concentration and time. The equation above predicts that the concentration of A will decrease in a smooth exponential curve over time. By taking the natural logarithm of each side of the equation and rearranging, we obtain an alternative logarithmic expression of the relationship between the concentration of A and t:

ln[A] = ln[A]₀ – kt

Because this equation has the form of the algebraic equation for a straight line, y = mx + b, with y = ln [A] and b = ln[A]₀, a plot of ln [A] versus t for a first-order reaction should give a straight line with a slope of −k and an intercept of ln[A]₀. Either the differential rate law or the integrated rate law can be used to determine whether a particular reaction is first order.

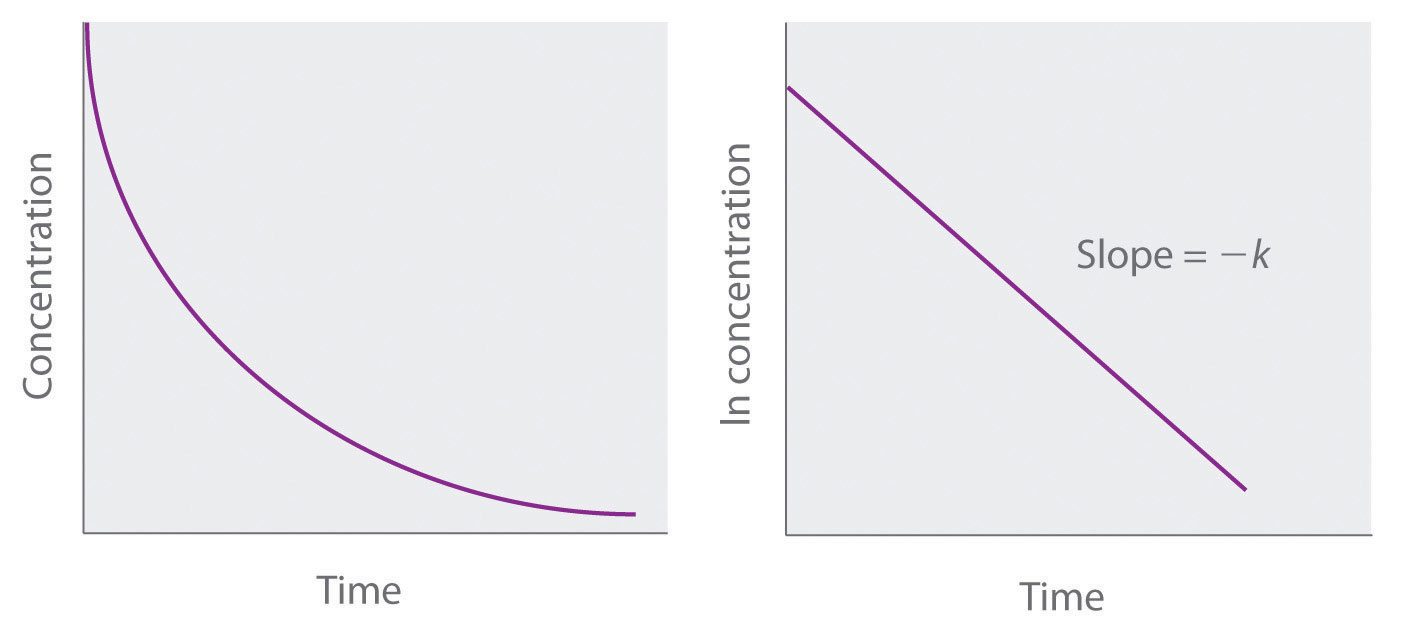
Figure 7.3.5. Graphs of a first-order reaction. The expected shapes of the curves for plots of reactant concentration versus time (top) and the natural logarithm of reactant concentration versus time (bottom) for a first-order reaction.

First-order reactions are very common. One reaction that exhibits apparent first-order kinetics is the hydrolysis of the anticancer drug cisplatin.

Cisplatin, the first “inorganic” anticancer drug to be discovered, is unique in its ability to cause complete remission of the relatively rare, but deadly cancers of the reproductive organs in young adults. The structures of cisplatin and its hydrolysis product are as follows:

Both platinum compounds have four groups arranged in a square plane around a Pt(II) ion. The reaction shown above is important because cisplatin, the form in which the drug is administered, is not the form in which the drug is active. Instead, at least one chloride ion must be replaced by water to produce a species that reacts with deoxyribonucleic acid (DNA) to prevent cell division and tumor growth. Consequently, the kinetics of the reaction have been studied extensively to find ways of maximizing the concentration of the active species.

The rate law and reaction order of the hydrolysis of cisplatin are determined from experimental data, such as those displayed in the table below. The table lists initial rate data for four experiments in which the reaction was run at pH 7.0 and 25°C but with different initial concentrations of cisplatin. Because the reaction rate increases with increasing cisplatin concentration, we know this cannot be a zeroth-order reaction. Comparing Experiments 1 and 2 in the table shows that the reaction rate doubles [(1.8 × 10⁻⁵ M/min) ÷ (9.0 × 10⁻⁶ M/min) = 2.0] when the concentration of cisplatin is doubled (from 0.0060 M to 0.012 M). Similarly, comparing Experiments 1 and 4 shows that the reaction rate increases by a factor of 5 [(4.5 × 10⁻⁵ M/min) ÷ (9.0 × 10⁻⁶ M/min) = 5.0] when the concentration of cisplatin is increased by a factor of 5 (from 0.0060 M to 0.030 M). Because the reaction rate is directly proportional to the concentration of the reactant, the exponent of the cisplatin concentration in the rate law must be 1, so the rate law is rate = k[cisplatin]¹. Thus the reaction is first order. Knowing this, we can calculate the rate constant using the differential rate law for a first-order reaction and the data in any row of the table. For example, substituting the values for Experiment 3 into the differential rate law,

3.6 × 10⁻⁵ M/min = k(0.024 M)

1.5 × 10⁻³ min⁻¹ = k

Knowing the rate constant for the hydrolysis of cisplatin and the rate constants for subsequent reactions that produce species that are highly toxic enables hospital pharmacists to provide patients with solutions that contain only the desired form of the drug.

Example 7.3.5 – The Integrated Rate Law for a First-Order Reaction – 1

If a sample of ethyl chloride with an initial concentration of 0.0200 M is heated at 650°C, what is the concentration of ethyl chloride after 10 h? How many hours at 650°C must elapse for the concentration to decrease to 0.0050 M (k = 1.6 × 10⁻⁶ s⁻¹)?

Solution

The exponential form of the integrated rate law for a first-order reaction is [A] = [A]₀e^−kt.

Having been given the initial concentration of ethyl chloride ([A]₀) and having the rate constant of k = 1.6 × 10⁻⁶ s⁻¹, we can use the rate law to calculate the concentration of the reactant at a given time t. Substituting the known values into the integrated rate law,

[CH₃CH₂Cl]_{10 h} = [CH₃CH₂Cl]₀e^-kt

= 0.0200 M(e^{-(1.6 x 10^-6 s^- 1) [(10 h)(60 min/h)(60s/min)]})

= 0.0189 M

We could also have used the logarithmic form of the integrated rate law:

ln[CH₃CH₂Cl]_{10 h} = ln[CH₃CH₂Cl]₀ – kt

= ln 0.0200 – (1.6 x 10^-6 s^-1 ) [(10 h)(60 min/h)(60s/min)]

[CH₃CH₂Cl]_{10 h} = e^-3.970 M

= 0.0189 M

To calculate the amount of time required to reach a given concentration, we must solve the integrated rate law for t. Using the integrated rate law gives the following:

ln[CH₃CH₂Cl]_t = ln[CH₃CH₂Cl]₀ – kt

kt = ln[CH₃CH₂Cl]₀ – ln[CH₃CH₂Cl]_t = ln[CH3CH2Cl]0[CH3CH2Cl]t

t = 1k(ln[CH₃CH₂Cl]₀[CH3CH2Cl]_t) = 11.6×10^-6s^-1 (ln0.0200 M 0.0050 M) = 8.7 x 10⁵ s = 240h = 2.4×10²h

Check Your Learning 7.3.6 – The Integrated Rate Law for a First-Order Reaction – 1

You find that the decomposition of sulfuryl chloride (SO₂Cl₂) is first order, and you calculate the rate constant at 320°C to be 2.2 × 10^-5 s^-1. Use the form(s) of the integrated rate law to find the amount of SO₂Cl₂ that remains after 20 h if a sample with an original concentration of 0.123 M is heated at 320°C. The equation for the decomposition of SO₂Cl₂ is:

SO₂Cl₂ (g)   →   SO₂ (g) + Cl₂ (g)

How long would it take for 90% of the SO₂Cl₂ to decompose?

Answer

0.0252 M; 29 h

Example 7.3.6 – The Integrated Rate Law for a First-Order Reaction – 2

The rate constant for the first-order decomposition of cyclobutane, C₄H₈ at 500°C is 9.2 × 10⁻³ s⁻¹:

C₄H₈  →  2C₂H₄

How long will it take for 80.0% of a sample of C₄H₈ to decompose?

Solution

We use the integrated form of the rate law to answer questions regarding time:

ln ([A]₀[A]) = kt

There are four variables in the rate law, so if we know three of them, we can determine the fourth. In this case we know [A]₀, [A], and k, and need to find t.

The initial concentration of C₄H₈, [A]₀, is not provided, but the provision that 80.0% of the sample has decomposed is enough information to solve this problem. Let x be the initial concentration, in which case the concentration after 80.0% decomposition is 20.0% of x or 0.200x. Rearranging the rate law to isolate t and substituting the provided quantities yields:

Check Your Learning 7.3.7 – The Integrated Rate Law for a First-Order Reaction – 2

Iodine-131 is a radioactive isotope that is used to diagnose and treat some forms of thyroid cancer. Iodine-131 decays to xenon-131 according to the equation:

I-131 → Xe-131 + electron

The decay is first-order with a rate constant of 0.138 d⁻¹. All radioactive decay is first order. How many days will it take for 90% of the iodine−131 in a 0.500 M solution of this substance to decay to Xe-131?

Answer

16.7 days

Example 7.3.7 – Determination of Reaction Order by Graphing

Show that the data below can be represented by a first-order rate law by graphing ln [H₂O₂] versus time. Determine the rate constant for the rate of decomposition of H₂O₂ from this data.

Solution

The data from above with the addition of values of ln[H₂O₂] are given in Figure 7.3.6.

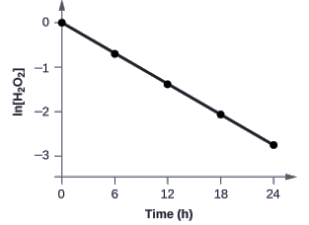
Figure 7.3.6. The linear relationship between the ln[H₂O₂] and time shows that the decomposition of hydrogen peroxide is a first-order reaction.

The plot of ln[H₂O₂] versus time is linear, thus we have verified that the reaction may be described by a first-order rate law.

The rate constant for a first-order reaction is equal to the negative of the slope of the plot of ln[H₂O₂] versus time where:

In order to determine the slope of the line, we need two values of ln[H₂O₂] at different values of t (one near each end of the line is preferable). For example, the value of ln[H₂O₂] when t is 6.00 h is −0.693; the value when t = 12.00 h is −1.386:

Check Your Learning 7.3.8 – Determination of Reaction Order by Graphing

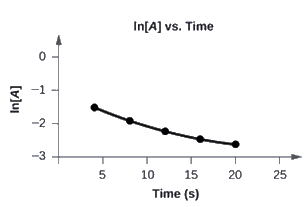
Graph the following data to determine whether the reaction A → B + C is first order.

Answer

The plot of ln[A] vs. t is not a straight line. The equation is not first order:

Half-Life of First-Order Reactions

We can derive an equation for determining the half-life of a first-order reaction from the alternate form of the integrated rate law as follows:

If we set the time t equal to the half-life, t_1/2, the corresponding concentration of A at this time is equal to one-half of its initial concentration.

Hence, when t = t_1/2, [A] = 12[A]₀.

Therefore

Thus:

 

We can see that the half-life of a first-order reaction is inversely proportional to the rate constant k and entirely independent of the concentration. A fast reaction (shorter half-life) will have a larger k; a slow reaction (longer half-life) will have a smaller k.

Example 7.3.8 – Calculation of a First-Order Rate Constant using Half-Life

Calculate the rate constant for the first-order decomposition of hydrogen peroxide in water at 40°C, using the data given in Figure 7.3.7.

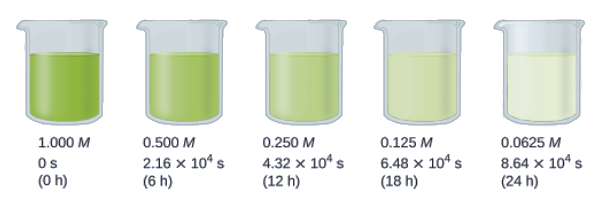
Figure 7.3.7. The decomposition of H₂O₂ (2H₂O₂  →  2H₂O + O₂) at 40°C is illustrated. The intensity of the color symbolizes the concentration of H₂O₂ at the indicated times; H₂O₂ is actually colorless.

Solution

The half-life for the decomposition of H₂O₂ is 2.16 × 10⁴ s:

Check Your Learning 7.3.9 – Calculation of a First-Order Rate Constant using Half-Life

The first-order radioactive decay of iodine-131 exhibits a rate constant of 0.138 d⁻¹. What is the half-life for this decay?

Answer

5.02 d.

Second-Order Reactions

The simplest kind of second-order reaction is one whose rate is proportional to the square of the concentration of one reactant. These generally have the form 2A → products. A second kind of second-order reaction has a reaction rate that is proportional to the product of the concentrations of two reactants. Such reactions generally have the form A + B → products. An example of the former is a dimerization reaction, in which two smaller molecules, each called a monomer, combine to form a larger molecule (a dimer).

The differential rate law for the simplest second-order reaction in which 2A → products is as follows:

Equation 7.3.4 Second-Order Differential Rate Law

Consequently, doubling the concentration of A quadruples the reaction rate. For the units of the reaction rate to be moles per liter per second (M/s), the units of a second-order rate constant must be the inverse (M⁻¹·s⁻¹). Because the units of molarity are expressed as mol/L, the unit of the rate constant can also be written as L(mol·s).

For the reaction 2A → products, the following integrated rate law describes the concentration of the reactant at a given time:

Because this equation has the form of an algebraic equation for a straight line, y = mx + b, with y = 1/[A] and b = 1/[A]₀, a plot of 1/[A] versus t for a simple second-order reaction is a straight line with a slope of k and an intercept of 1/[A]₀.

Simple second-order reactions are common. In addition to dimerization reactions, two other examples are the decomposition of NO₂ to NO and O₂ and the decomposition of HI to I₂ and H₂. Most examples involve simple inorganic molecules, but there are organic examples as well. We can follow the progress of the reaction described in the following paragraph by monitoring the decrease in the intensity of the red color of the reaction mixture.

Many cyclic organic compounds that contain two carbon–carbon double bonds undergo a dimerization reaction to give complex structures. One example is as follows:

For simplicity, we will refer to this reactant and product as “monomer” and “dimer,” respectively. The systematic name of the monomer is 2,5-dimethyl-3,4-diphenylcyclopentadienone. The systematic name of the dimer is the name of the monomer followed by “dimer.” Because the monomers are the same, the general equation for this reaction is 2A → product. This reaction represents an important class of organic reactions used in the pharmaceutical industry to prepare complex carbon skeletons for the synthesis of drugs. Like the first-order reactions studied previously, it can be analyzed using either the differential rate law or the integrated rate law .

Table 7.3.3 Time to Rate to Concentration

To determine the differential rate law for the reaction, we need data on how the reaction rate varies as a function of monomer concentrations, which are provided in the table above. From the data, we see that the reaction rate is not independent of the monomer concentration, so this is not a zeroth-order reaction. We also see that the reaction rate is not proportional to the monomer concentration, so the reaction is not first order. Comparing the data in the second and fourth rows shows that the reaction rate decreases by a factor of 2.8 when the monomer concentration decreases by a factor of 1.7:

and

Because (1.7)² = 2.9 ≈ 2.8, the reaction rate is approximately proportional to the square of the monomer concentration.

rate ∝ [monomer]²

This means that the reaction is second order in the monomer. Using the differential rate law and the data from any row in the table, we can calculate the rate constant. Substituting values at time 10 min, for example, gives the following:

We can also determine the reaction order using the integrated rate law. To do so, we use the decrease in the concentration of the monomer as a function of time for a single reaction, plotted in part (a) in Figure 7.3.8. The measurements show that the concentration of the monomer (initially 5.4 × 10⁻³ M) decreases with increasing time. This graph also shows that the reaction rate decreases smoothly with increasing time. According to the integrated rate law for a second-order reaction, a plot of 1/[monomer] versus t should be a straight line, as shown in part (b) in Figure 7.3.8. Any pair of points on the line can be used to calculate the slope, which is the second-order rate constant. In this example, k = 4.1 M⁻¹·min⁻¹, which is consistent with the result obtained using the differential rate equation. Although in this example the stoichiometric coefficient is the same as the reaction order, this is not always the case. The reaction order must always be determined experimentally.

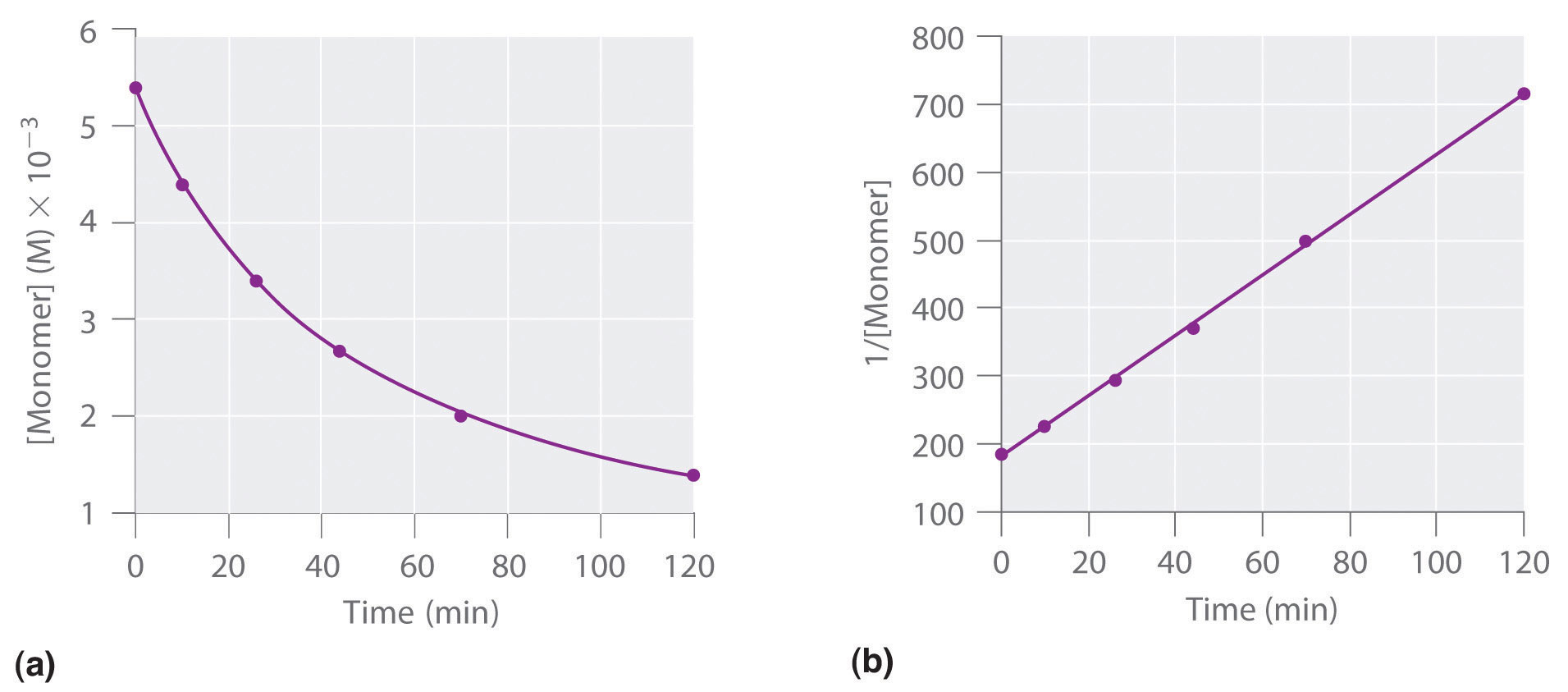
Figure 7.3.8. These plots correspond to dimerization of the monomer as (a) the experimentally determined concentration of monomer versus time and (b) 1/[monomer] versus time. The straight line in (b) is expected for a simple second-order reaction.

For two or more reactions of the same order, the reaction with the largest rate constant is the fastest. Because the units of the rate constants for zeroth-, first-, and second-order reactions are different, however, we cannot compare the magnitudes of rate constants for reactions that have different orders.

In addition to the simple second-order reaction and rate law we have just described, another very common second-order reaction has the general form A + B → products, in which the reaction is first order in A and first order in B. The differential rate law for this reaction is as follows:

Because the reaction is first order both in A and in B, it has an overall reaction order of 2. (The integrated rate law for this reaction is rather complex, so we will not describe it.) We can recognize second-order reactions of this sort because the reaction rate is proportional to the concentrations of each reactant.

Example 7.3.9 – The Integrated Rate Law for a Second-Order Reaction – 1

The reaction of butadiene gas (C₄H₆) with itself produces C₈H₁₂ gas as follows:

2C₄H₆ (g)  →  C₈H₁₂ (g)

The reaction is second order with a rate constant equal to 5.76 × 10⁻² L/mol/min under certain conditions. If the initial concentration of butadiene is 0.200 M, what is the concentration remaining after 10.0 min?

Solution

We use the integrated form of the rate law to answer questions regarding time. For a second-order reaction, we have:

We know three variables in this equation: [A]₀ = 0.200 mol/L, k = 5.76 × 10⁻² L/mol/min, and t = 10.0 min. Therefore, we can solve for [A], the fourth variable:

[A] = 1.79 x 10⁻¹ mol L⁻¹

Therefore 0.179 mol/L of butadiene remains at the end of 10.0 min, compared to the 0.200 mol/L that was originally present.

Check Your Learning 7.3.10 – The Integrated Rate Law for a Second-Order Reaction – 1

If the initial concentration of butadiene is 0.0200 M, what is the concentration remaining after 20.0 min?

Answer

0.0195 mol/L

Example 7.3.10 – The Integrated Rate Law for a Second-Order Reaction – 2

At high temperatures, nitrogen dioxide decomposes to nitric oxide and oxygen.

2NO₂ (g)  →  2NO (g) + O₂ (g)

If a flask that initially contains 0.056 M NO₂ is heated at 300°C, what will be the concentration of NO₂ after 1.0 h? How long will it take for the concentration of NO₂ to decrease to 10% of the initial concentration? Use the integrated rate law for a second-order reaction and the rate constant k = 0.54 M^-1·s^-1.

Solution

We know k and [NO₂]₀, and we are asked to determine [NO₂] at t = 1 h (3600 s). Substituting the appropriate values,

Thus [NO₂]₃₆₀₀ = 5.1 × 10⁻⁴ M.

I this case, we know k and [NO₂]₀, and we are asked to calculate at what time [NO₂] = 0.1[NO₂]₀ = 0.1(0.056 M) = 0.0056 M. To do this, we solve the integrated rate law for t, using the concentrations given.

NO₂ decomposes very rapidly; under these conditions, the reaction is 90% complete in only 5.0 min.

Check Your Learning 7.3.11 – The Integrated Rate Law for a Second-Order Reaction – 2

When the highly reactive species HO₂ forms in the atmosphere, one important second-order reaction that then removes it from the atmosphere is as follows:

2HO₂ (g)  →  H₂O₂ (g) + O₂ (g)

You calculate the rate constant for the decomposition of HO₂ as k = 1.4 × 10⁹ M⁻¹·s⁻¹. This high rate constant means that HO₂ decomposes rapidly under the reaction conditions given in the problem. In fact, the HO₂ molecule is so reactive that it is virtually impossible to obtain in high concentrations. Given a 0.0010 M sample of HO₂, calculate the concentration of HO₂ that remains after 1.0 h at 25°C. How long will it take for 90% of the HO₂ to decompose? Use the integrated rate law for a second-order reaction and the rate constant k = 1.4 × 10⁹ M^-1ᐧs^-1.

Answer

2.0 × 10⁻¹³ M; 6.4 × 10⁻⁶ s

Example 7.3.11 – Determination of Reaction Order by Graphing

The data below are for the same reaction described in the example “The Integrated Rate Law for a Second-Order Reaction – 1”. Test these data to confirm that this dimerization reaction is second-order.

Solution

In order to distinguish a first-order reaction from a second-order reaction, we plot ln [C₄H₆] versus t and compare it with a plot of 1[C4H6] versus t. The values needed for these plots follow.

The plots are shown in Figure 7.3.9. As you can see, the plot of ln [C₄H₆] versus t is not linear, therefore the reaction is not first order. The plot of 1[C4H6] versus t is linear, indicating that the reaction is second order.

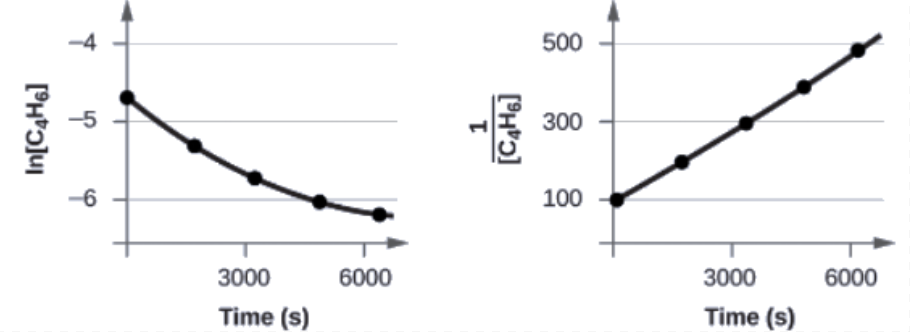
Figure 7.3.9. These two graphs show first- and second-order plots for the dimerization of C₄H₆. Since the first-order plot (left) is not linear, we know that the reaction is not first order. The linear trend in the second-order plot (right) indicates that the reaction follows second-order kinetics.

Check Your Learning 7.3.12 – Determination of Reaction Order by Graphing

Does the following data fit a second-order rate law?

Answer

Yes. The plot of 1[A] vs. t is linear:

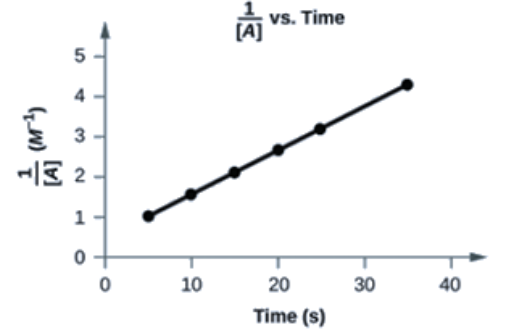
Half-Life of Second-Order Reactions

We can derive the equation for calculating the half-life of a second order as follows:

or

If

t = t_1/2

then

[A] = 12[A]₀

and we can write:

Thus:

 

For a second-order reaction, t_1/2 is inversely proportional to the concentration of the reactant (hence its half-life is dependent on the concentration), and the half-life increases as the reaction proceeds because the concentration of reactant decreases. Consequently, we find the use of the half-life concept to be more complex for second-order reactions than for first-order reactions. Unlike with first-order reactions, the rate constant of a second-order reaction cannot be calculated directly from the half-life unless the initial concentration is known.

Questions

★ Questions

Note: Reminder that the units used in rate law equations will differ from each other based on their order.

In the reaction 4A + 3B  →  2C + 3D reaction A is found to disappear at a rate of 5.1 X 10^-5 Ms^-1

What is the rate of reaction?

What is the rate of disappearance of B?

What is the rate of formation of C?

In the reaction 3A + 2B  →  C + 2D reaction A is found to disappear at a rate of 4.6 x 10^-5 Ms^-1

What is the rate of reaction?

What is the rate of disappearance of reactant B?

What is the rate of appearance for product D?

In the reaction A  →  B, [A] is found to be 0.750 M at t = 61.2s and 0.704 M at t = 73.5s. Determine the average rate of the reaction during this time interval.

What is the average rate of reaction over a time interval for [A] if it is 0.455 M at t = 80.25s and 0.474 M at t = 82.4s?

For the reaction A + 2B  →  2C, the rate of reaction is 1.75 x 10^-5 Ms^-1 at the time when [A] = 0.3575 M.

What is the rate of formation of C?

What will [A] be 1 minute later?

Assume the rate remains at 1.75 x 10-5M s-1. How long would it take for [A] to change from 0.3580 to 0.3500M?

The initial rate of the reaction A + B  →  C + D is determined for different initial conditions, with the results listed in the table.

Expt[A]	M[B]	MInitial Rate M s-1
10.185	0.144	3.35 x 10-4
20.185	0.288	1.35 x 10-3
30.370	0.144	6.75 x 10-4
40.370	0.288	2.70 x 10-3

What is the order of reaction with respect to A and to B?

What is the overall reaction order?

What is the value of the rate constant, k?

The initial rate of the reaction A + B  →  C + D is determined for different initial conditions, with the results listed in the table:

Expt[A]	M[B]	MInitial Rate M s-1
10.331	0.203	2.205 x 10-4
20.331	0.406	8.82 x 10-4
30.662	0.203	4.41 x 10-4
40.662	0.406	1.7 x 10-3

What is the order of reaction with respect to A and B?

What is the overall reaction order?

What is the value of the rate constant k?

The initial rate of the reaction A + B  →  C + D is determined for difference initial conditions, with the results listed in the table:

Expt[A]	M[B]	MInitial Rate M s-1
10.241	0.153	1.261 x 10-4
20.241	0.306	5.044 x 10-4
30.482	0.153	2.522 x 10-4
40.482	0.306	6.741 x 10-4

What is the order of the reaction with respect of A and B? Write out respective rate laws for A and B

What is the overall reaction order?

What is the value of the k, the rate constant?

The first-order reaction A→products has t_1/2 = 300s

What percent of sample A remains unreacted 1000 s after the reaction starts?

What is the rate of reaction when [A] = 0.25M?

 

A first order reaction A→products has a half life of 120 seconds calculate the following:

What percentage of A remains unreacted after 800 seconds of reaction?

What is the rate of reaction at [A] = 0.25M?

 

The first order reaction has t_1/2 of 250s.

What percent of a sample of A remains unreacted 1500s after a reaction starts?

What if the rate of the reaction is 1/2 the rate of disappearance of A?

★★ Questions

The reaction A→products is first order in A

If 4.2g A decomposes for 45 minutes, the undecomposed A is measured to be 1.05g. What is the half-life, t_1/2, of this reaction (in minutes)?

Starting with the same 4.2 g, what is the mass (in grams) of undecomposed A after 75 minutes?

Explain why

A reaction rate cannot be calculated from solely the collision frequency.

The rate of a chemical reaction may increase dramatically with temperature, whereas the collision frequency rises a lot more slowly.

Introducing a catalyst to a reaction mixture can have such a significant impact on the rate of the reaction, even if the temperature is held constant.

Answer the following:

What two factors does the rate of a reaction depend on other than the frequency of collisions?

Why does the rate of reaction increase dramatically with temperature?

What is the net effect of the addition of a catalyst?

Answers

Rate of disappearance of B = reaction rate X coefficient of B

(1.3 x 10^-5 M s^-1)(3) = 3.9×10^-5 M s^-1

Rate of formation of C = reaction rate X coefficient of C

(1.3 x 10^-5 M s^-1)(2) = 2.6×10^-5 M s^-1

Rate of disappearance of B = (rate of reaction) X 2(coefficient of B)

(1.5 x 10^-5 M s^-1)(2) = 3.1×10^-5 M s^-1

Same process as B) (multiply rate of reaction by 2) OR:

Rate of appearance of D = -13(2)(Δ[A]Δt) = -23(4.6×10^-5 M s^-1) = 3.1×10^-5 M s^-1

Rate of disappearance of B = reaction rate X coefficient of B

(1.3 x 10^-5 M s^-1)(3) = 3.9×10^-5 M s^-1

Rate of formation of C = reaction rate X coefficient of C

(1.3 x 10^-5 M s^-1)(2) = 2.6×10^-5 M s^-1

(a) Order with respect to A = 1, Order with respect to B = 2; (b) overall order of reaction = 3; (c) 0.103 M s^-1

Order of Reaction with respect to B:

Find where A is constant and B changes (Reaction 1 and Reaction 2)

Divide: Reaction2 / Reaction1 = 8.82×10^-4 2.205×10^-4 = [0.331]^m[0.406]ⁿ[0.331]^m[0.203]ⁿ

Thus the reaction is second order with respect to B.

Order of Reaction with respect to A:

Find where B is constant and A changes (Reaction 1 and Reaction 2)

Divide: Reaction3 / Reaction1 = 4.41×10^-4 2.205×10^-4 = [0.406]^m[0.662]ⁿ[0.203]^m[0.662]ⁿ

Reaction3 / Reaction1 = 2 = 2m → m = 1

Thus the reaction is second order with respect to A

b) Reaction order = reaction order of A + reaction order of B = 3rd order reaction

c) 2.205 x 10^-4 = k x [0.331][0.203]2k = 1.6 x 10^-2

Reaction is first order with respect to A

Overall reaction order = (reaction order of A + reaction order of B) = 1 + 2 = 3rd order overall

k = 0.0224 M^-2s^-1

ln(%unreacted) = -kt

k = ln2 t_1/2 = ln2300 s = 0.0023 s^-1

ln(%unreacted) = -(0.0023 ^s-1)(1000 s) = -2.3

Rate = k[A]

Rate = 0.0023 s^-1

[0.25 M] = 5.74 x 10^-4 M s^-1

t_1/2 (first order) = ln2k

k = ln2 t_1/2 = ln2 120 s = 5.77×10^-3

percent unreacted defined by [A]_t[A]₀

For a first order reaction, rate = k[C] = 0.0046/s x 0.25 = 1.15 x 10^-3 M/s

k = ln2 t_1/2 = 0.693250s = 0.00277s-1

ln(%unreacted) = -kt = (-.00277 s^-1)(1500 s) = -4.155

%unreacted = 0.0157 x 100% = 1.57% of the original quantity

Rate = k[A] = (0.00277 s^-1)(0.5 M) = 0.00139 M/s

(4.2 g)(14) = 1.05 g → 2 halflives have passed → 45minutes / 2 = t_1/2 = 22.5 minutes

k = ln2 t_1/2 = ln2 22.5minutes = 0.0308 min^-1

[A]_t = [A]₀ e^-2.31

[A]_t = (4.2 g)(0.09926) = 0.417 g A