3.3 – First Law of Thermodynamics

The relationship between internal energy, heat, and work can be represented by the equation:

ΔU = q + w

This is one version of the first law of thermodynamics which states that “energy is neither created nor destroyed, only transferred”, and it shows that the internal energy of a system changes through heat flow into or out of the system (positive q is heat flow in; negative q is heat flow out) or work is done on or by the system. The work, w, is positive if it is done on the system and negative if it is done by the system. In the case of PV work, we can consider work done on the system as contraction, while work done by the system is expansion.

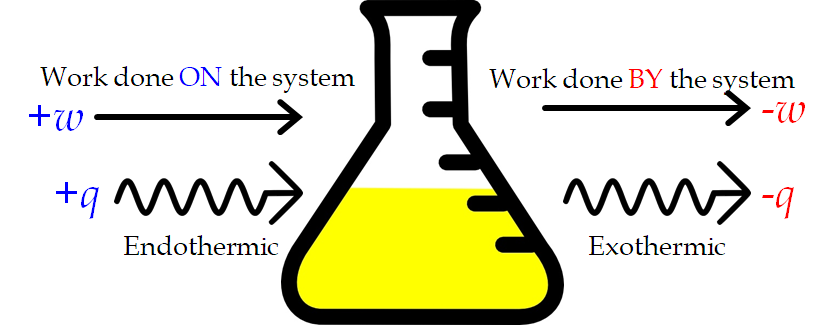
Figure 3.3.1. Sign conventions for heat and work. Work done on the system or heat absorbed by the system are positive. Work done by the system or heat produced by the system are negative. These can happen in any combination..

As we discussed in section 3.1, energy in the universe is constant/fixed. We can relate this to internal energy by saying that, while energy can be transferred between the system and the surroundings, the change in internal energy of the universe is equal to zero.

ΔU_universe = ΔU_system + ΔU_surroundings = 0

There are many forms of work, such as electrical and mechanical work, but in this course, the relevant type of work is called expansion work (or pressure-volume work). Expansion work occurs when a system pushes back the surroundings against a restraining pressure, or when the surroundings compress the system. An example of this occurs during the operation of an internal combustion engine. The reaction of gasoline and oxygen is exothermic. Some of this energy is given off as heat, and some does work pushing the piston in the cylinder. The substances involved in the reaction are the system, and the engine and the rest of the universe are the surroundings. The system loses energy by both heating and doing work on the surroundings, and its internal energy decreases. We will consider how to determine the amount of work involved in a chemical or physical change in the chapter on thermodynamics.

This view of an internal combustion engine illustrates the conversion of energy produced by the exothermic combustion reaction of a fuel such as gasoline into energy of motion. To learn more about the first law of thermodynamics, check out this video.

State Functions

As discussed, the relationship between internal energy, heat, and work can be represented as ΔU = q + w. Internal energy is a type of quantity known as a state function, whereas heat and work are not state functions (typically referred to as path functions). The value of a state function depends only on the state that a system is in, and not on how that state is reached. If a quantity is not a state function, then its value does depend on how the state is reached. An example of a state function is altitude or elevation. If you stand on the summit of Mt. Kilimanjaro, you are at an altitude of 5895 m, and it does not matter whether you hiked there or parachuted there. The distance you travelled to the top of Kilimanjaro, however, is not a state function. You could climb to the summit by a direct route or by a more roundabout, circuitous path (Figure 3.3.2.). The distances travelled would differ (distance is not a state function) but the elevation reached would be the same (altitude is a state function).

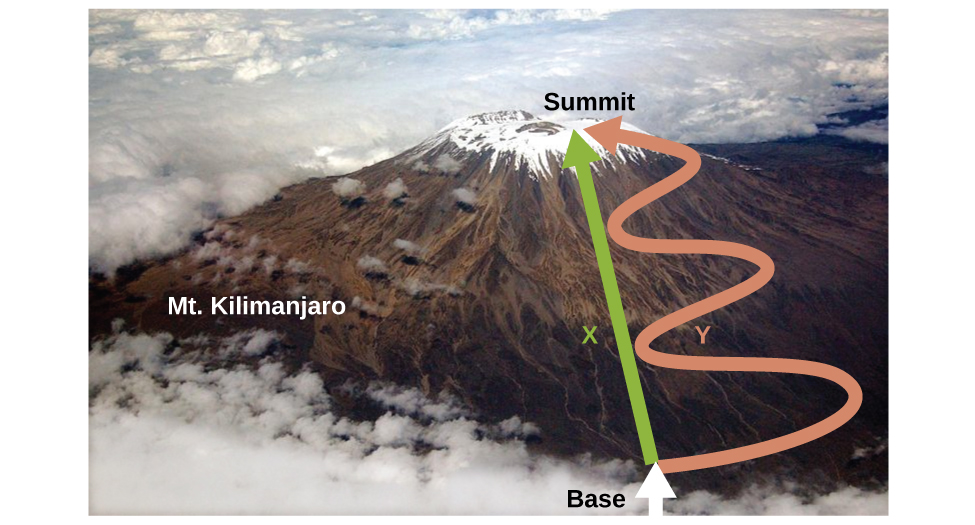
Figure 3.3.2. Paths X and Y represent two different routes to the summit of Mt. Kilimanjaro. Both have the same change in elevation (altitude or elevation on a mountain is a state function; it does not depend on path), but they have very different distances travelled (distance walked is not a state function; it depends on the path). (credit: modification of work by Paul Shaffner)

Regarding energy, work and heat are both path functions, but internal energy is not. This means the path taken to get to the results matters when calculating w or q, but need not be taken into account when solving for ΔU.

Energy Diagrams

When working with systems involving both heat and work, it is often useful to visualize the transition from the initial to the final energy states using a diagram (Figure 3.3.3.).

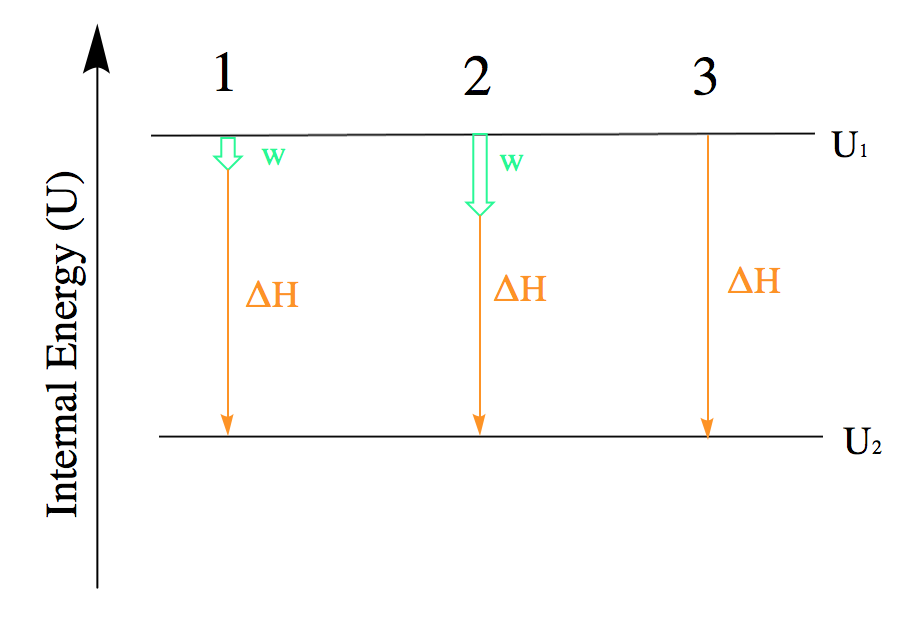
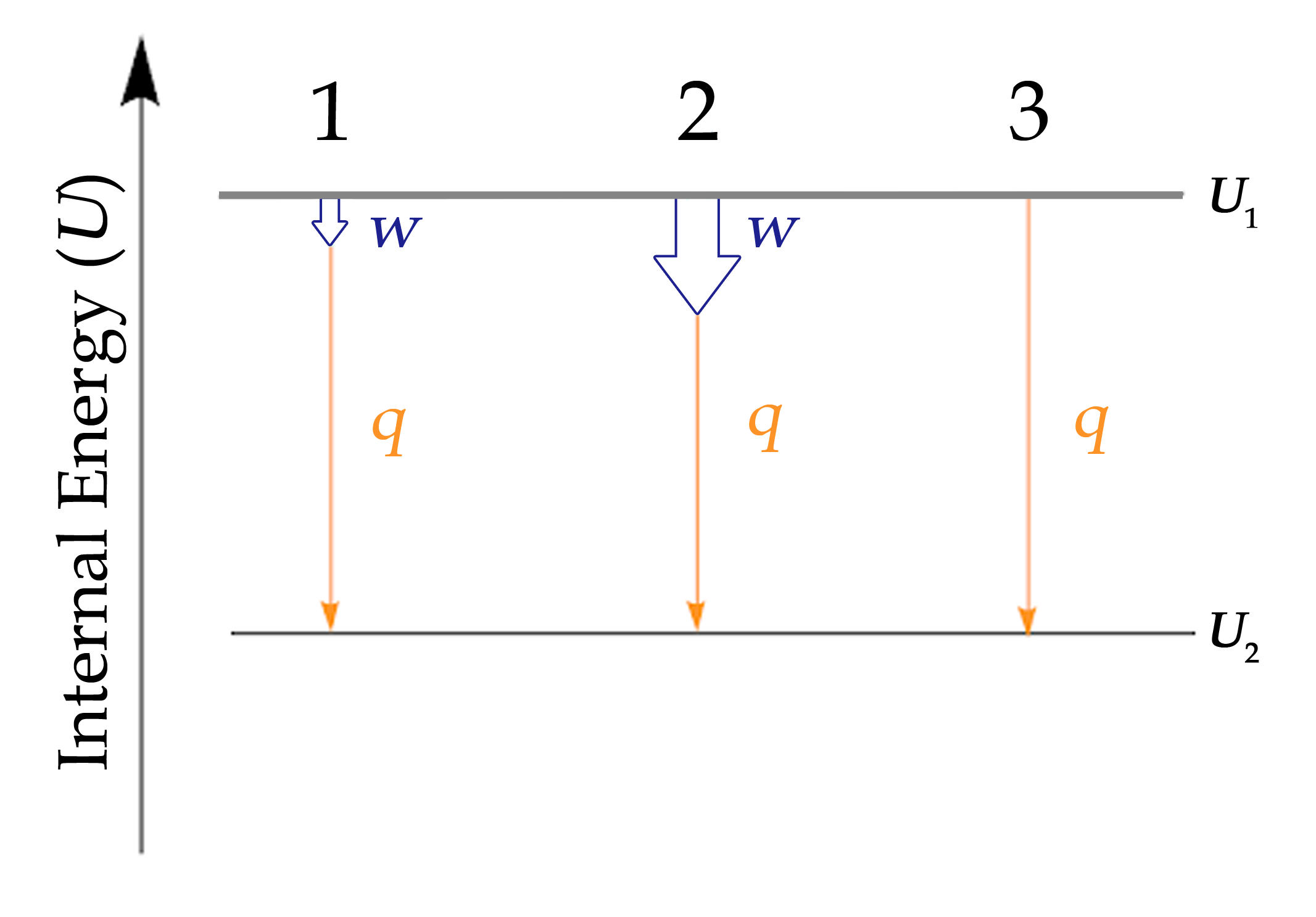
Figure 3.3.3. The internal energy of three processes from which the system loses energy. 1: Depiction of the change in internal energy essentially equal to the heat transfer. Mathematically: ΔU ≈ q. 2: Depiction of the change in internal energy where both work is done and heat is lost. Mathematically: ΔU = q + w. 3: Depiction of the change in internal energy when no work is done but heat is lost. Mathematically: ΔU = q

Although Figure 3.3.3. only shows processes for which a system loses energy, this tactic should be used whenever possible and can be modified for instances in which work and heat have different signs. This will be covered more in Hess’ law.

Questions

★ Questions

1. A sample of an ideal gas is allowed to expand from an initial volume of 0.200 L to a final volume of 3.50 L against a constant external pressure of 0.995 atm. At the same time, 117 J of heat is transferred from the surroundings to the gas. What is the total change in the internal energy (ΔU) of the gas in joules?

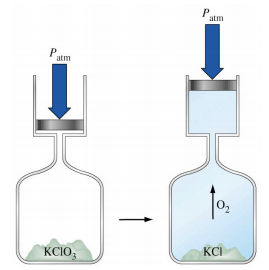
2. When potassium chlorate decomposes it produces oxygen gas. From the system’s point of view (which is the convention), w is:
            A. Positive

B. Negative

C. Zero

3. What is the work when a gas contracts from 3.45 L to 0.97 L under an external pressure of 0.985 atm?

★★ Questions

4. The volume of a gas changes from 264 mL to 971 mL at constant temperature. Calculate the amount of work done by the gas (in joules) if it expands (a) against a vacuum and (b) against a constant pressure of 4.00 atm.

5. For the following reactions, indicate if work will increase, decrease or remain constant. Hint: remember that work is based on PV – so how is the volume changing in each reaction?

         a. 2 H₂O (l)  →  2 H₂ (g) + O₂ (g)

         b. NO₂ (g) + O₃ (g)  →  NO₃ (g) + O₂ (g)

         c. CH₄ (g) + 2 O₂ (g)  →  CO₂ (g) + 2 H₂O (l)

Answers

1. -216 J

     2. B

     3. 248 J

     4. (a) 0 J, no work is done; (b) -287 J

     5. (a) w increases because the moles of gas increase which would increase the             volume of gas. (b) there is no change due to both sides of the reaction having the      same number of moles. (c) decrease due to the different amounts of gases on              both sides of the reaction, the reactant side has a larger number of moles of gas.