3.4 – Enthalpy

What is Enthalpy?

Chemists ordinarily use a property known as enthalpy (H) to describe the thermodynamics of chemical and physical processes. Enthalpy is defined as the sum of a system’s internal energy (U) and the mathematical product of its pressure (P) and volume (V):

H = U + PV

Equation 3.4.1 Enthalpy

Since it is derived from three state functions (U, P, and V), enthalpy is also a state function. Enthalpy values for specific substances cannot be measured directly; only enthalpy changes for chemical or physical processes can be determined. For processes that take place at constant pressure (a common condition for many chemical and physical changes), the enthalpy change (ΔH) is:

ΔH = ΔU + PΔV

Equation 3.4.2 Enthalpy Change

When pressure is constant, the mathematical product PΔV represents work (w), namely, expansion or pressure-volume work as noted. By their definitions, the arithmetic signs of ΔV and w will always be opposite:

PΔV = -w

Equation 3.4.3 Work

Substituting this equation and the definition of internal energy into the enthalpy-change equation yields:

ΔH = ΔU + PΔV

ΔH = (q_P + w) – w

ΔH = q_P

Equation 3.4.4 Substituted Enthalpy Change

where q_P is the heat of reaction under conditions of constant pressure. Thus, enthalpy is defined as the quantity of heat transferred under constant pressure conditions.

And so, if a chemical or physical process is carried out at constant pressure with the only work done caused by expansion or contraction, then the heat flow (q_P) and enthalpy change (ΔH) for the process are equal.

The heat given off when you operate a Bunsen burner is equal to the enthalpy change of the methane combustion reaction that takes place since it occurs at the essentially constant pressure of the atmosphere. On the other hand, the heat produced by a reaction measured in a bomb calorimeter ([link]) is not equal to ΔH because the closed, constant-volume metal container prevents expansion work from occurring. Chemists usually perform experiments under normal atmospheric conditions, at constant external pressure with q = ΔH, which makes enthalpy the most convenient choice for determining heat.

Comparing ΔH and ΔU

If ΔH for a reaction is known, we can use the change in the enthalpy of the system to calculate its change in internal energy:

ΔH = ΔU + PΔV

When a reaction does not involve gases (i.e. involves only solids, liquids, liquid solutions, or any combination of these, the volume does not change appreciably (ΔV ≈ 0). Under these conditions, we can simplify the equation above where PΔV gets cancelled out:

Reaction with no gases  →  ΔH ≈ ΔU

When a reaction does involve gases, however, ΔH and ΔU can differ significantly. We can calculate ΔU from the measured value of ΔH by modifying the right side of the equation, PΔV, with the ideal gas law, PV = nRT. P and T remain constant, so we recognize that

PΔV= (Δn_gas)RT

Where

We can rewrite the equation for the change in enthalpy as follows:

Reaction with gases  →  ΔH = ΔU + Δn_gasRT

Where

 Δn_gas = n_products – n_reactants

This equation applies if

Δn_gas ≠ 0

However, if

Δn_gas = 0

:

ΔH = ΔU

Equation 3.4.5 Enthalpy Change, Potential Change

Enthalpy Changes in Reactions

The following conventions apply when we use ΔH:

1. Chemists use a thermochemical equation to represent the changes in both matter and energy. In a thermochemical equation, the enthalpy change of a reaction is shown as a ΔH value following the equation for the reaction. This ΔH value indicates the amount of heat associated with the reaction involving the number of moles of reactants and products as shown in the chemical equation. For example, consider this equation:

H₂ (g) + 1/2 O₂ (g)  →  H₂O (l)          ΔH = – 286 kJ

This equation indicates that when 1 mole of hydrogen gas and 1/2 moles of oxygen gas at some temperature and pressure change to 1 mole of liquid water at the same temperature and pressure, 286 kJ of heat are released to the surroundings. If the coefficients of the chemical equation are multiplied by some factor, the enthalpy change must be multiplied by that same factor (ΔH is an extensive property):

(two-fold increase in amounts)

2 H₂ (g) + O₂ (g)  →  2 H₂O (l)        ΔH = 2 × (- 286 kJ) = – 572 kJ

(two-fold decrease in amounts)

1/2 H₂ (g) + 1/4 O₂ (g)  →  1/2 H₂O (l)                 ΔH = 1/2 × (- 286 kJ) = -143 kJ

2. The enthalpy change of a reaction depends on the physical state of the reactants and products of the reaction (whether we have gases, liquids, solids, or aqueous solutions), so these must be shown. For example, when 1 mole of hydrogen gas and

H₂ (g) + 1/2 O₂ (g)  →  H₂O (l)         ΔH = – 286 kJ

A negative value of an enthalpy change, ΔH, indicates an exothermic reaction; a positive value of ΔH indicates an endothermic reaction (Figure 3.4.1). If the direction of a chemical equation is reversed, the arithmetic sign of its ΔH is changed (a process that is endothermic in one direction is exothermic in the opposite direction).

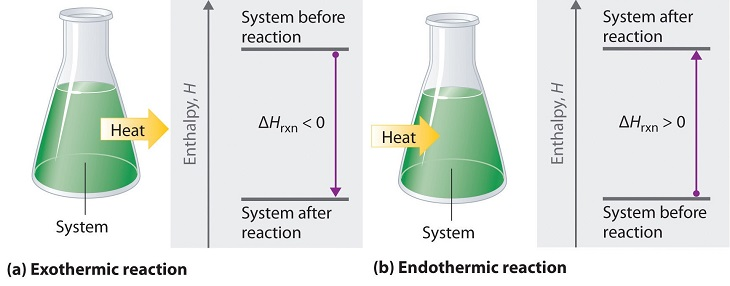
Figure 3.4.1. Energy changes in chemical reactions are usually measured as changes in enthalpy. (a) If heat flows from a system to its surroundings, the enthalpy of the system decreases, ΔH_rxn is negative, and the reaction is exothermic; it is energetically downhill. (b) Conversely, if heat flows from the surroundings to a system, the enthalpy of the system increases, ΔH_rxn is positive, and the reaction is endothermic; it is energetically uphill.

Example 3.4.1 – Measurement of an Enthalpy Change

When 0.0500 mol of HCl (aq) reacts with 0.0500 mol of NaOH (aq) to form 0.0500 mol of NaCl (aq), 2.9 kJ of heat is produced. What is ΔH, the enthalpy change, per mole of acid reacting, for the acid-base reaction run under the conditions described in the OpenStax Chemistry Resource 

HCl (aq) + NaOH (aq) → NaCl (aq) + H₂O (l)

Solution

For the reaction of 0.0500 mol acid (HCl), q = −2.9 kJ. This ratiocan be used as a conversion factor to find the heat produced when 1 mole of HCl reacts:

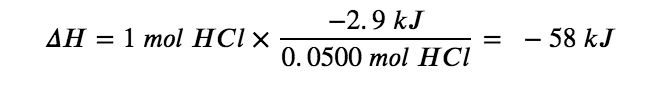
The enthalpy change when 1 mole of HCl reacts is −58 kJ. Since that is the number of moles in the chemical equation, we write the thermochemical equation as:

HCl (aq) + NaOH (aq)  →  NaCl (aq) + H₂O (l)       ΔH = – 58 kJ

Check Your Learning 3.4.1 – Measurement of an Enthalpy Change

When 1.34 g Zn (s) reacts with 60.0 mL of 0.750 M HCl (aq), 3.14 kJ of heat are produced. Determine the enthalpy change per mole of zinc reacting for the reaction:

Zn (s) + 2 HCl (aq)  →  ZnCl₂ (aq) + H₂ (g)

Answer

ΔH = − 153 kJ

Be sure to take both stoichiometry and limiting reactants into account when determining the ΔH for a chemical reaction.

Example 3.4.2 – Another Example of the Measurement of an Enthalpy Change

A gummy bear contains 2.67 g sucrose, C₁₂H₂₂O₁₁. When it reacts with 7.19 g potassium chlorate, KClO₃, 43.7 kJ of heat are produced. Determine the enthalpy change for the reaction:

C₁₂H₂₂O₁₁ (aq) + 8 KClO₃ (aq) → 12 CO₂ (g) + 11 H₂O (l) + 8 KCl (aq)

Solution

We have:

available, and

available. Since

is needed, C₁₂H₂₂O₁₁ is the excess reactant and KClO₃ is the limiting reactant. The reaction uses 8 mol KClO₃, and the conversion factor is

so we have

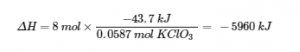
The enthalpy change for this reaction is −5960 kJ, and the thermochemical equation is:

C₁₂H₂₂O₁₁ (aq) + 8 KClO₃ (aq)  →  12 CO₂ (g) + 11 H₂O (l) + 8 KCl (aq)

ΔH = – 5960 kJ

Check Your Learning 3.4.2 – Another Example of the Measurement of an Enthalpy Change

When 1.42 g of iron reacts with 1.80 g of chlorine, 3.22 g of FeCl₂ (s) and 8.60 kJ of heat is produced. What is the enthalpy change for the reaction when 1 mole of FeCl₂ (s) is produced?

Answer

ΔH = − 338 kJ

Enthalpy changes are typically tabulated for reactions in which both the reactants and products are at the same conditions. A standard state is a commonly accepted set of conditions used as a reference point for the determination of properties under other different conditions. For chemists, the IUPAC standard state refers to materials under a pressure of 1 bar and solutions at 1 M and does not specify a temperature. Many thermochemical tables list values with a standard state of 1 atm. Because the ΔH of a reaction changes very little with such small changes in pressure (1 bar = 0.987 atm), ΔH values (except for the most precisely measured values) are essentially the same under both sets of standard conditions. We will include a superscript “o” in the enthalpy change symbol to designate standard state. Since the usual (but not technically standard) temperature is 298.15 K, we will use a subscripted “298” to designate this temperature (note: this differs from the STP for gases, don’t confuse them!). Thus, the symbol (ΔH°₂₉₈) is used to indicate an enthalpy change for a process occurring under these conditions. (The symbol ΔH is used to indicate an enthalpy change for a reaction occurring under nonstandard conditions.)

The enthalpy changes for many types of chemical and physical processes are available in the reference literature, including those for combustion reactions, phase transitions, and formation reactions. As we discuss these quantities, it is important to pay attention to the extensive nature of enthalpy and enthalpy changes. Since the enthalpy change for a given reaction is proportional to the amounts of substances involved, it may be reported on that basis (i.e., as the ΔH for specific amounts of reactants). However, we often find it more useful to divide one extensive property (ΔH) by another (amount of substance), and report a per-amount intensive value of ΔH, often “normalized” to a per-mole basis. (Note that this is similar to determining the intensive property-specific heat from the extensive property heat capacity, which we will see in the next topic).

Questions

★ Questions

1. When 100 mL of 0.200 M NaCl (aq) and 100 mL of 0.200 M AgNO₃ (aq), both at 21.9 °C, are mixed in a coffee cup calorimeter (we will discover what these are used for in the next topic), the temperature increases to 23.5 °C as solid AgCl forms. Calculate ΔH in kJ/mol of AgNO₃ (aq) for the reaction:

NaCl (aq) + AgNO₃ (aq)  →  AgCl (s) + NaNO₃ (aq)

  2. When solid ammonium nitrate dissolves in water, the solution becomes cold.          This is the basis for an “instant ice pack”. When 3.21 g of solid NH₄NO₃ dissolves in    50.0 g of water at 24.9 °C in a calorimeter, the temperature decreases to 20.3 °C.        Calculate the enthalpy of solution (ΔH for the dissolution) per mole of NH₄NO₃.

  3. Qualitatively compare ΔH and ΔU for each of the following reactions:

         a. AgNO₃ (aq) + NaCl (aq)  →  AgCl (s) + NaNO₃ (aq)

         b. H₂ (g) + F₂ (g)  →  2 HF (g)

         c. C₃H₈ (g) + 5 O₂ (g)  →  3 CO₂ (g) + 4 H₂O (g)

  4. Calculate ΔH for the reaction described by the equation. (Hint: use the value for    the approximate amount of heat absorbed by the reaction that you calculated in a    previous exercise.)

Ba(OH)₂ ∙ 8H₂O (s) + 2 NH₄SCN (aq)  →  Ba(SCN)₂ (aq) + 2 NH₃ (aq) + 10 H₂O (l)

  5. How much heat is produced by combustion of 125 g of methanol under standard    state conditions?

  6. How many moles of isooctane must be burned to produce 100 kJ of heat under      standard state conditions?

  7. What mass of carbon monoxide must be burned to produce 175 kJ of heat under    standard state conditions?

  8. When 2.50 g of methane burns in oxygen, 125 kJ of heat is produced. What is          the enthalpy of combustion per mole of methane under these conditions?

Answers

1. 1.34 x 10³ kJ/mol

We assume that the calorimeter prevents heat transfer between the solution and its external environment (including the calorimeter itself), in which case:

q_rxn = – q_soln

with “rxn” and “soln” used as shorthand for “reaction” and “solution,” respectively.

Assuming also that the specific heat of the solution is the same as that for water, we have:

q_rxn = – q_soln = – (c × m × ΔT)_soln

=[(4.184 J/g∘C) × (53.2 g) × (20.3∘C – 24.9∘C)]

=[(4.184 J/g∘C) × (53.2 g) × (- 4.6∘C)]

+1.0 × 10³ J = + 1.0 kJ

The positive sign for q indicates that the dissolution is an endothermic process.

  3. (a) ΔU ≈ ΔH: since there are no gases the volume change is negligible (basically      equal to 0) meaning that ΔU ≈ q_P and since ΔH = q_P then ΔU ≈ ΔH; (b) ΔU = ΔH:        Δn = 0 mol which means there is no work done, therefore ΔU = ΔH; (c) ΔU > ΔH:        Δn = 1 mol resulting in w = – RT. – RT will always be negative therefore, under              constant pressure, ΔU = ΔH – RT demonstrating ΔU > ΔH.

  4. 95.72 kJ/mol

  5. 2836.3 kJ

  6. 1.83 × 10⁻² mol

  7. 17.3 g

  8. 802 kJ/mol