4.3 – Solving Equilibrium Problems
We know that at equilibrium, the value of the reaction quotient of any reaction is equal to its equilibrium constant. Thus, we can use the mathematical expression for Q to determine a number of quantities associated with a reaction at equilibrium or approaching equilibrium. While we have learned to identify in which direction a reaction will shift to reach equilibrium, we want to extend that understanding to quantitative calculations. We do so by evaluating the ways that the concentrations of products and reactants change as a reaction approaches equilibrium, keeping in mind the stoichiometric ratios of the reaction. This algebraic approach to equilibrium calculations will be explored in this section.
Relative Changes in Concentration
Changes in concentrations or pressures of reactants and products occur as a reaction system approaches equilibrium. In this section we will see that we can relate these changes to each other using the coefficients in the balanced chemical equation describing the system. We use the decomposition of ammonia as an example.
On heating, ammonia reversibly decomposes into nitrogen and hydrogen according to this equation:
2 NH3 (g) ⇌ N2 (g) + 3 H2 (g)
If a sample of ammonia decomposes in a closed system and the concentration of N2 increases by 0.11 mol/L, the change in the N2 concentration, Δ[N2] = [N2]f – [N2]i, is 0.11 M. The change is positive because the concentration of N2 increases.
The change in the H2 concentration, Δ[H2], is also positive—the concentration of H2 increases as ammonia decomposes. The chemical equation tells us that the change in the concentration of H2 is three times the change in the concentration of N2 because for each mole of N2 produced, 3 moles of H2 are produced.
[H2] = 3 × [N2]
= 3 × 0.11 mol/L = 0.33 mol/L
The change in concentration of NH3, Δ[NH3], is twice that of Δ[N2]; the equation indicates that 2 moles of NH3 must decompose for each mole of N2 formed. However, the change in the NH3 concentration is negative because the concentration of ammonia decreases as it decomposes.
∆[NH3] = – 2 × ∆[N2] = – 2 × 0.11 mol/L = – 0.22 mol/L
We can relate these relationships directly to the coefficients in the equation
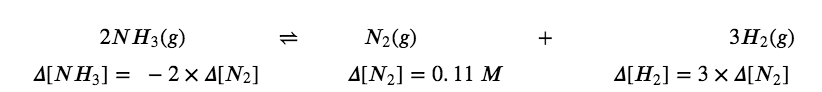
Note that all the changes on one side of the arrows are of the same sign and that all the changes on the other side of the arrows are of the opposite sign.
If we did not know the magnitude of the change in the concentration of N2, we could represent it by the symbol +x.
The changes in the other concentrations would then be represented as:
∆[H2] = 3 × ∆[N2] = + 3x
∆[NH3] = – 2 × ∆[N2] = – 2x
The coefficients in the Δ terms are identical to those in the balanced equation for the reaction.
| 2 NH3 (g) ⇌ | N2 (g) + | 3 H2 (g) |
| -2x | +x | + 3x |
The simplest way for us to find the coefficients for the concentration changes in any reaction is to use the coefficients in the balanced chemical equation. The sign of the coefficient is positive when the concentration increases; it is negative when the concentration decreases.
Example 4.3.1 – Determining Relative Changes in Concentration
Complete the changes in concentrations for each of the following reactions.
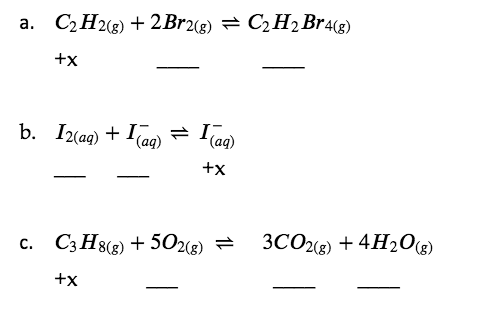
Solution

Check Your Learning 4.3.1 – Determining Relative Changes in Concentration
Complete the changes in concentrations for each of the following reactions:
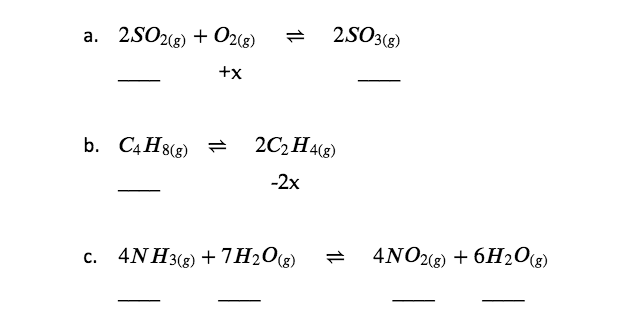
Answer
(a) + 2x, + x, − 2x; (b) + x, − 2x; (c) + 4x, + 7x, − 4x, − 6x or − 4x, − 7x, + 4x, + 6x
Calculations Involving Equilibrium Concentrations or Pressures
Because the value of the reaction quotient of any reaction at equilibrium is equal to its equilibrium constant, we can use the mathematical expression for Q to determine a number of quantities associated with a reaction at equilibrium. It may help if we keep in mind that Q = K (at equilibrium) in all of these situations and that there are only two basic types of equilibrium problems:
- Calculation of an equilibrium constant. If concentrations/partial pressures of reactants and products at equilibrium are known, the value of the equilibrium constant for the reaction can be calculated.
- Calculation of equilibrium concentrations/partial pressures. If the value of the equilibrium constant and all of the equilibrium concentrations/pressures, except one, are known, the remaining unknown can be calculated. In addition, if the value of the equilibrium constant and a set of concentrations or pressures of reactants and products that are not at equilibrium are known, the quantity at equilibrium can be calculated.
In the following discussion, we will examine examples of equilibrium calculations involving solutes and values of K in concentration units (KC). However, please note that the problem-solving procedures equally hold for reactions involving gases and values of K in pressure units (KP).
Calculation of an Equilibrium Constant
In order to calculate an equilibrium constant, enough information must be available to determine the equilibrium concentrations of all reactants and products. Armed with the concentrations, we can solve the equation for K, as it will be the only unknown.
In the previous section, we learned how to determine the equilibrium constant of a reaction if we know the concentrations of reactants and products at equilibrium. The following example shows how to use the stoichiometry of the reaction and a combination of initial concentrations and equilibrium concentrations to determine an equilibrium constant. This technique, commonly called an ICE chart – for Initial, Change, and Equilibrium – will be helpful in solving many equilibrium problems. A chart is generated beginning with the equilibrium reaction in question. The initial concentrations of the reactants and products are provided in the first row of the ICE table (these essentially time-zero concentrations that assume no reaction has taken place). The next row of the table contains the changes in concentrations that result when the reaction proceeds toward equilibrium (don’t forget to account for the reaction stoichiometry). The last row contains the concentrations once equilibrium has been reached.
Example 4.3.2 – Calculation of an Equilibrium Constant – 1
Iodine molecules react reversibly with iodide ions to produce triiodide ions.
I2 (aq) + I– (aq) ⇌ I3– (aq)
If a solution with the concentrations of I2 and I− both equal to 1.000 × 10−3 mol/L before reaction gives an equilibrium concentration of I2 of 6.61 × 10−4 mol/L, what is the equilibrium constant for the reaction?
Solution
We will begin this problem by calculating the changes in concentration as the system goes to equilibrium. Then we determine the equilibrium concentrations and, finally, the equilibrium constant. First, we set up a table with the initial concentrations, the changes in concentrations, and the equilibrium concentrations using −x as the change in concentration of I2.
I2+I−⇌ I3−
|
|
I2 |
I– |
I3– |
|
Initial Concentration (mol/L) |
1.000 x 10−3 | 1.000 x 10−3 | 0 |
|
Change (mol/L) |
–𝑥 | –𝑥 | +𝑥 |
|
Equilibrium concentration (mol/L) |
1.000 x 10−3 – 𝑥 | 1.000 x 10−3 – 𝑥 | +𝑥 |
Since the equilibrium concentration of I2 is given, we can solve for x. At equilibrium the concentration of I2 is 6.61 × 10−4 M, therefore:
1.000 × 10-3 – x = 6.61 × 10-4
x = 1.000 × 10-3 – 6.61 × 10-4
x = 3.39 × 10-4 mol/L
Now we can fill in the table with the concentrations at equilibrium.
I2+I−⇌ I3−
| I2 | I− | I3− | |
| Initial Concentration (mol/L) | 1.000 x 10−3 | 1.000 x 10−3 | 0 |
| Change (mol/L) | –𝑥 = -3.39 x 10−4 | –𝑥 | +𝑥 |
| Equilibrium concentration (mol/L) | 6.61 x 10−4 | 6.61 x 10−4 | 3.39 x 10−4 |
We now calculate the value of the equilibrium constant.
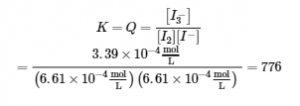
This value for K makes sense – it is close to 1, indicating that, at equilibrium, the system will contain comparable amounts of reactants and products. This is true when we look at the equilibrium concentration in the ICE table, or even visualize the close proximity of concentration curves (in a graph) of species when equilibrium is reached (Figure 4.3.1).
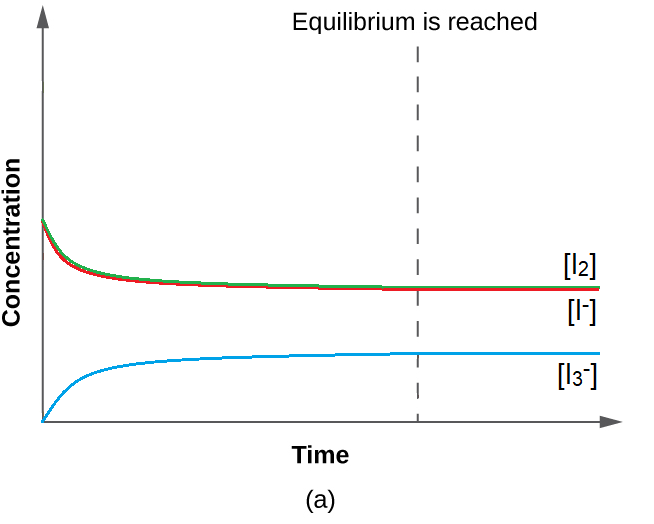
Figure 4.3.1. With a value of K relatively close to 1, the concentrations of reactants and products approach each other when the system moves towards equilibrium.
Check Your Learning 4.3.2 – Calculation of an Equilibrium Constant – 1
Ethanol and acetic acid react to form water and ethyl acetate, the solvent responsible for the odor of some nail polish removers:
C2H5OH + CH3CO2H ⇌ CH3CO2C2H5 + H2O
When 1.00 mol each of C2H5OH and CH3CO2H are allowed to react in 1 L of the solvent dioxane, equilibrium is established when 0.13 mol of each of the reactants remains. Calculate the equilibrium constant for the reaction. (Note: Water is not a solvent in this reaction.)
Answer
KC = 45
Example 4.3.3 – Calculation of an Equilibrium Constant – 2
A 1.00 mol sample of NOCl was placed in a 2.00 L reactor and heated to 227°C until the system reached equilibrium. The contents of the reactor were then analyzed and found to contain 0.056 mol of Cl2. Calculate KC at this temperature. The equation for the decomposition of NOCl to NO and Cl2 is as follows:
2 NOCl (g) ⇌ 2 NO (g) + Cl2 (g)
Solution
The first step in any such problem is to balance the chemical equation for the reaction (if it is not already balanced) and use it to derive the equilibrium constant expression. In this case, the equation is already balanced, and the equilibrium constant expression is as follows:
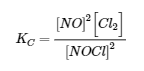
Initially, the system contains 1.00 mol of NOCl in a 2.00 L container. Thus [NOCl]i = 1.00 mol/2.00 L = 0.500 mol/L. The initial concentrations of NO and Cl2 are 0 mol/L because initially no products are present. Moreover, we are told that at equilibrium the system contains 0.056 mol of Cl2 in a 2.00 L container, so [Cl2]f = 0.056 mol/2.00 L = 0.028 mol/L. We insert these values into the following table:
|
2 NOCl (g) ⇌ 2 NO (g) + Cl2 |
|||
|
|
[NOCl] |
[NO] |
[Cl2] |
|
Initial concentration (mol/L) |
0.500 |
0 |
0 |
|
Change (mol/L) |
|
|
|
|
Equilibrium concentration (mol/L) |
|
|
0.028 |
We use the stoichiometric relationships given in the balanced chemical equation to find the change in the concentration of Cl2, the substance for which initial and final concentrations are known:
Δ[Cl2] = [0.028 mol/L (final) − 0.00 mol/L (initial)] = + 0.028 mol/L
According to the coefficients in the balanced chemical equation, 2 mol of NO are produced for every 1 mol of Cl2, so the change in the NO concentration is as follows: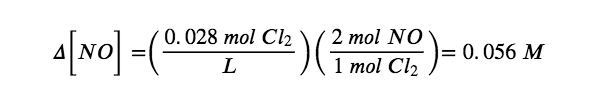
Similarly, 2 mol of NOCl are consumed for every 1 mol of Cl2 produced, so the change in the NOCl concentration is as follows:
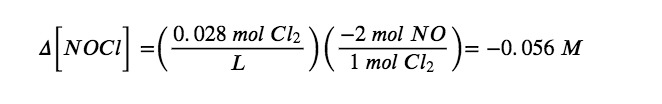 We insert these values into our table:
We insert these values into our table:
|
2 NOCl (g) ⇌ 2 NO (g) + Cl2 |
|||
|
|
[NOCl] |
[NO] |
[Cl2] |
| Initial concentration (M) |
0.500 |
0 |
0 |
| Change (M) |
-0.056 |
+0.056 |
+0.028 |
| Equilibrium concentration (M) |
|
|
0.028 |
We sum the numbers in the [NOCl] and [NO] columns to obtain the final concentrations of NO and NOCl:
[NO]f = 0.000 M + 0.056 M = 0.056 M
[NOCl]f = 0.500 M + (−0.056 M) = 0.444 M
We can now complete the table:
|
2 NOCl (g) ⇌ 2 NO (g) + Cl2 |
|||
|
|
[NOCl] |
[NO] |
[Cl2] |
| Initial concentration (M) |
0.500 |
0 |
0 |
| Change (M) |
-0.056 |
+0.056 |
+0.028 |
| Equilibrium concentration (M) |
0.444 |
0.056 |
0.028 |
We can now calculate the equilibrium constant for the reaction:
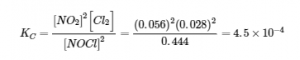
Check Your Learning 4.3.3 – Calculation of an Equilibrium Constant – 2
The German chemist Fritz Haber (1868–1934; Nobel Prize in Chemistry 1918) was able to synthesize ammonia (NH3) by reacting 0.1248 M H2 and 0.0416 M N2 at about 500°C (Figure 4.3.2). At equilibrium, the mixture contained 0.00272 M NH3. What is KC for the reaction N2 + 3H2 ⇌ 2NH3 at this temperature? What is the value of KP?

Figure 4.3.2.The original laboratory apparatus designed by Fritz Haber and Robert Le Rossignol in 1908 for synthesizing ammonia from its elements. A metal catalyst bed, where ammonia was produced, is in the large cylinder at the left. The Haber-Bosch process used for the industrial production of ammonia uses essentially the same process and components but on a much larger scale. Unfortunately, Haber’s process enabled Germany to prolong World War I when German supplies of nitrogen compounds, which were used for explosives, had been exhausted in 1914.
Answer
KC = 0.105; KP = 2.61 × 10−5
Calculation of Equilibrium Concentration(s)
In these types of equilibrium problems, if we know the equilibrium constant for a reaction and know the concentrations at equilibrium of all reactants and products except one, we can calculate the missing concentration.
Example 4.3.4 – Calculation of a Missing Equilibrium Concentration
Nitrogen oxides are air pollutants produced by the reaction of nitrogen and oxygen at high temperatures. At 2000°C, the value of the equilibrium constant KC for the reaction, N2 (g) + O2 (g) ⇌ 2 NO (g), is 4.1 × 10−4. Calculate the equilibrium concentration of NO (g) in air at 1.00 atm pressure and 2000°C. The equilibrium concentrations of N2 and O2 at this pressure and temperature are 0.036 M and 0.0089 M, respectively.
Solution
We are given all of the equilibrium concentrations except that of NO. Thus, we can solve for the missing equilibrium concentration by rearranging the equation for the equilibrium constant.
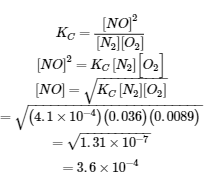
Thus [NO] is 3.6 × 10−4 mol/L at equilibrium under these conditions.
We can check our answer by substituting all equilibrium concentrations into the expression for the reaction quotient, QC, to see whether it is equal to the equilibrium constant, and thus confirm that the system is indeed at equilibrium.
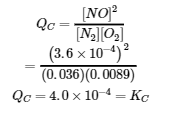
The answer checks; our calculated value gives the equilibrium constant within the error associated with the significant figures in the problem.
Check Your Learning 4.3.4 – Calculation of a Missing Equilibrium Concentration
The equilibrium constant for the reaction of nitrogen and hydrogen to produce ammonia at a certain temperature is 6.00 × 10−2. Calculate the equilibrium concentration of ammonia if the equilibrium concentrations of nitrogen and hydrogen are 4.26 M and 2.09 M, respectively.
Answer
1.53 mol/L
In another scenario, if we know the equilibrium constant for a reaction and a set of concentrations of reactants and products that are not at equilibrium, we can calculate the changes in concentrations as the system comes to equilibrium, as well as the new concentrations at equilibrium. The typical procedure can be summarized in four steps.
1. Determine the direction the reaction proceeds to come to equilibrium.
a. Write a balanced chemical equation for the reaction.
b. If the direction in which the reaction must proceed to reach equilibrium is
not readily obvious, calculate Q from the initial values and compare it to K to
determine the direction of change.
2. Determine the relative changes needed to reach equilibrium, then write the
equilibrium concentrations in terms of these changes.
a. Define the changes in the initial concentrations that are needed for the
reaction to reach equilibrium. Generally, we represent the smallest change
with the symbol x and express the other changes in terms of the smallest
change.
b. Define missing equilibrium concentrations in terms of the initial
concentrations and the changes in concentration determined in (a).
3. Solve for the change and the equilibrium concentrations.
a. Substitute the equilibrium concentrations into the expression for the
equilibrium constant, solve for x, and check any assumptions used to find x.
b. Calculate the equilibrium concentrations.
4. Check the arithmetic.
5. Check the calculated equilibrium concentrations by substituting them into the
equilibrium expression and determining whether they give the equilibrium
constant.
Sometimes a particular step may differ from problem to problem—it may be more complex in some problems and less complex in others. However, every calculation of equilibrium concentrations from a set of initial concentrations will involve these steps.
In solving equilibrium problems that involve changes in concentration, it is again very convenient to set up an ICE table.
Example 4.3.5 – Calculation of Concentration Changes as a Reaction Goes to Equilibrium
Under certain conditions, the equilibrium constant KC for the decomposition of PCl5 (g) into PCl3 (g) and Cl2 (g) is 0.0211. What are the equilibrium concentrations of PCl5, PCl3, and Cl2 if the initial concentration of PCl5 was 1.00 M?
Solution
Use the stepwise process described earlier.
1. Determine the direction the reaction proceeds.
The balanced equation for the decomposition of PCl5 is
PCl5 (g) ⇌ PCl3 (g) + Cl2 (g)
Because we have no products initially, Q = 0 and the reaction must proceed to the right (towards products).
2. Determine the relative changes needed to reach equilibrium, then write the equilibrium concentrations in terms of these changes.
Let us represent the increase in concentration of PCl3 by the symbol x. The other changes may be written in terms of x by considering the coefficients in the chemical equation.
PCl5 (g) ⇌ PCl3 (g) + Cl2 (g)
– x + x + x
The changes in concentration and the expressions for the equilibrium concentrations are:
PCl5 ⇌ PCl3 + Cl2
|
|
PCl5 | PCl3 | Cl2 |
| Initial Concentration (M) | 1.00 | 0 | 0 |
| Change (M) | –𝑥 | +𝑥 | +𝑥 |
| Equilibrium concentration (M) | 1.00 –𝑥 | 0 + 𝑥 = 𝑥 | 0 + 𝑥 = 𝑥 |
3. Solve for the change and the equilibrium concentrations.
Substituting the equilibrium concentrations into the equilibrium constant equation gives
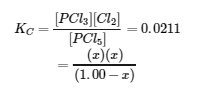
This equation contains only one variable, x, the change in concentration. We can write the equation as a quadratic equation and solve for x using the quadratic formula.
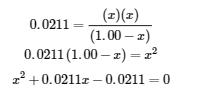
Appendix C shows us an equation of the form ax2 + bx + c = 0 can be rearranged to solve for x:
![]()
In this case, a = 1, b = 0.0211, and c = −0.0211. Substituting the appropriate values for a, b, and c yields:

| NOTE: |
|
Quadratic equations often have two different solutions: one that is physically possible and one that is physically impossible (an extraneous root). An extraneous root could be, for example, a negative value or one that is physically insignificant (e.g. if the “Change” in an ICE table is 0.100 – x, and one possible value for x is 0.300, then that value can’t be physically possible because that would yield a negative value for equilibrium concentration). |
In this case, the second solution (−0.156) is physically impossible because we know the change must be a positive number (otherwise we would end up with negative values for concentrations of the products). Thus, x = 0.135 M.
The equilibrium concentrations are
[PCl5] = 1.00 – 0.135 = 0.87 M
[PCl3] = x = 0.135 M
[Cl2] = x = 0.135 M
4. Check the arithmetic.
Substitution into the expression for Kc (to check the calculation) gives
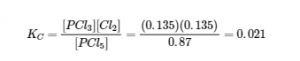
The equilibrium constant calculated from the equilibrium concentrations is equal to the value of Kc given in the problem (when rounded to the proper number of significant figures). Thus, the calculated equilibrium concentrations are confirmed.
Check Your Learning 4.3.5 – Calculation of Concentration Changes as a Reaction Goes to Equilibrium
Acetic acid, CH3CO2H, reacts with ethanol, C2H5OH, to form water and ethyl acetate, CH3CO2C2H5.
CH3CO2H + C2H5OH ⇌ CH3CO2C2H5 + H2O
The equilibrium constant for this reaction at a certain temperature, using dioxane as a solvent, is 4.0. What are the equilibrium concentrations when 0.15 mol CH3CO2H, 0.15 mol C2H5OH, 0.40 mol CH3CO2C2H5, and 0.40 mol H2O are mixed in enough dioxane solvent to make 1.0 L of solution?
Answer
[CH3CO2H] = 0.36 M, [C2H5OH] = 0.36 M, [CH3CO2C2H5] = 0.17 M, [H2O] = 0.17 M
Check Your Learning 4.3.6 – Calculation of Concentration Changes as a Reaction Goes to Equilibrium
A 1.00-L flask is filled with 1.00 moles of H2 and 2.00 moles of I2. The value of the equilibrium constant KC for the reaction of hydrogen and iodine reacting to form hydrogen iodide is 50.5 under the given conditions. What are the equilibrium concentrations of H2, I2, and HI in moles/L?
H2 (g) + I2 (g) ⇌ 2 HI (g)
Answer
[H2] = 0.06 M, [I2] = 1.06 M, [HI] = 1.88 M
Now let’s consider another example where we can utilize a square root shortcut method to facilitate problem-solving. If we find that the fractional term consisting of reactants (denominator) and products (numerator) has perfect squares, we can take the square root of both sides when solving for x.
Example 4.3.6 – Concentration Changes as a Reaction Goes to Equilibrium – Square Root Shortcut
The water–gas shift reaction is important in several chemical processes, such as the production of H2 for fuel cells. This reaction can be written as follows:
H2 (g) + CO2 (g) ⇌ H2O (g) + CO (g)
KC = 0.106 at 700 K. If a mixture of gases that initially contains 0.0150 M H2 and 0.0150 M CO2 is allowed to equilibrate at 700 K, what are the final concentrations of all substances present?
Solution
The initial concentrations of the reactants are [H2]i = [CO2]i = 0.0150 M. Just as before, we will focus on the change in the concentrations of the various substances between the initial and final states. If we define the change in the concentration of H2O as x, then Δ[H2O] = +x. We can use the stoichiometry of the reaction to express the changes in the concentrations of the other substances in terms of x. For example, 1 mol of CO is produced for every 1 mol of H2O, so the change in the CO concentration can be expressed as Δ[CO] = +x. Similarly, for every 1 mol of H2O produced, 1 mol each of H2 and CO2 are consumed, so the change in the concentration of the reactants is Δ[H2] = Δ[CO2] = −x. We enter the values in the following table and calculate the final concentrations.
|
H2 (g) + CO2 (g) ⇌ H2O (g) + CO (g) |
||||
|
|
[H2] |
[CO2] |
[H2O] |
[CO] |
| Initial concentration (M) |
0.0150 |
0.0150 |
0 |
0 |
| Change (M) |
– x |
– x |
+ x |
+ x |
| Equilibrium concentration (M) | (0.0150- x) | (0.0150 – x) |
+ x |
+ x |
We can now use the equilibrium equation and the given K to solve for x:
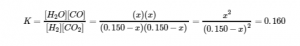
We could solve this equation with the quadratic formula, but it is far easier to solve for x by recognizing that the left side of the equation is a perfect square; that is,
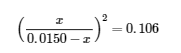
Taking the square root of both sides of this equation yields,

The final concentrations of all species in the reaction mixture are as follows:

We can check our work by inserting the calculated values back into the equilibrium constant expression:

To two significant figures, this KC is the same as the value given in the problem, so our answer is confirmed.
Check Your Learning 4.3.7 – Concentration Changes as a Reaction Goes to Equilibrium – Square Root Shortcut
Hydrogen gas reacts with iodine vapor to give hydrogen iodide according to the following chemical equation:
H2 (g) + I2 (g) ⇌ 2 HI (g)
KC = 54.0 at 425°C. If 0.172 M H2 and I2 are injected into a reactor and maintained at 425°C until the system equilibrates, what is the final concentration of each substance in the reaction mixture?
Answer
[HI]f = 0.270 M; [H2]f = [I2]f = 0.037 M
Sometimes it is possible to use chemical insight to find solutions to equilibrium problems without actually solving a quadratic (or more complicated) equation. First, however, it is useful to verify that equilibrium can be obtained starting from two extremes: all (or mostly) reactants and all (or mostly) products .
Consider the ionization of 0.150 M HA, a weak acid.
HA (aq) + H2O (l) ⇌ H3O+ (aq) + A– (aq) KC=6.80×10-4
The most obvious way to determine the equilibrium concentrations would be to start in a system containing only reactants. This could be called the “all reactant” starting point. Using x for the amount of acid ionized at equilibrium, this is the ICE table and solution.
HA (aq) + H2O (l) ⇌ H3O+ (aq) + A– (aq)
| Initial Concentration (M) | 0.150 |
─ |
0 | 0 |
| Change (M) | – x |
─ |
+x | +x |
| Equilibrium concentration (M) | 0.150 – x |
─ |
+x | +x |
Setting up and solving the quadratic equation gives
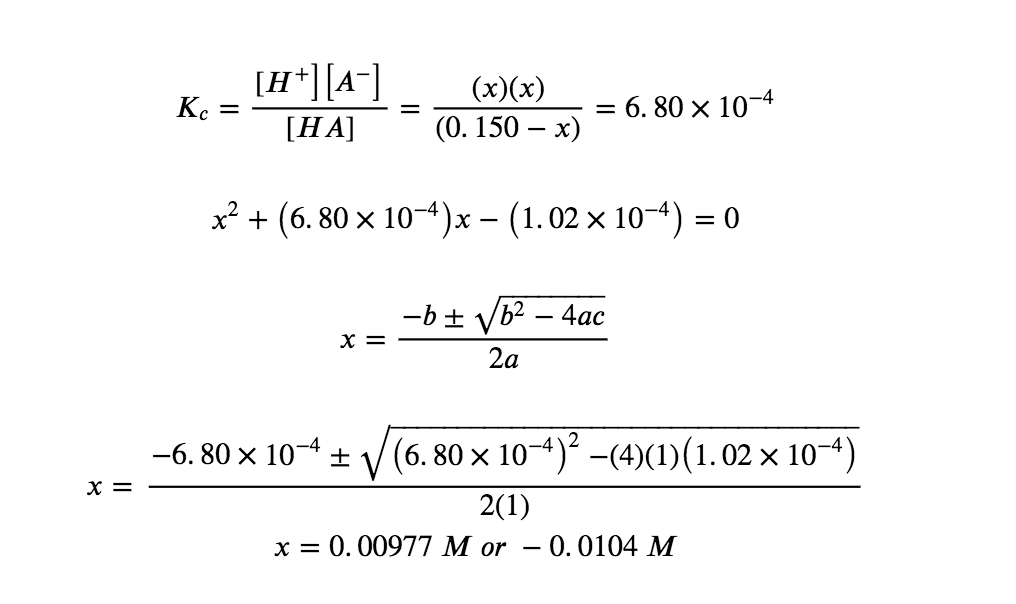
Using the positive (physical) root, the equilibrium concentrations are
[HA] = 0.150 – x = 0.140 M
[H3O+] = [A–] = x = 0.00977 M
A less obvious way to solve the problem would be to assume all the HA ionizes first, then the system comes to equilibrium. This could be called the “all product” starting point. Assuming all of the HA ionizes gives
[HA] = 0.150 – 0.150 = 0 M
[H3O+] = 0 + 0.150 = 0.150 M
[A–] = 0 + 0.150 = 0.150 M
Using these as initial concentrations and “y” to represent the concentration of HA at equilibrium, this is the ICE table for this starting point.
HA (aq) + H2O (l) ⇌ H3O+ (aq) + A– (aq)
|
Initial Concentration (M) |
0 | ─ | 0.150 | 0.150 |
|
Change (M) |
+y | ─ | – y | – y |
|
Equilibrium concentration (M) |
+y | ─ | 0.150 – y | 0.150 – y |
Setting up and solving the quadratic equation gives
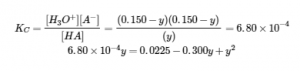
Retain a few extra significant figures to minimize rounding problems.

Rounding each solution to three significant figures gives
y = 0.160 M or y = 0.140 M
Using the physically significant root (0.140 M) gives the equilibrium concentrations as
[HA] = y = 0.140 M
[H3O+] = 0.150 – y = 0.010 M
[A–] = 0.150 – y = 0.010 M
Thus, the two approaches give the same results (to three decimal places), and show that both starting points lead to the same equilibrium conditions (Figure 4.3.3). The “all reactant” starting point resulted in a relatively small change (x) because the system was close to equilibrium, while the “all product” starting point had a relatively large change (y) that was nearly the size of the initial concentrations. Notice that the graph in part (a) of Figure 4.3.3 experiences little change in concentration; hence, it can be said that a system that starts “close” to equilibrium will require only a ”small” change in conditions (x) to reach equilibrium.
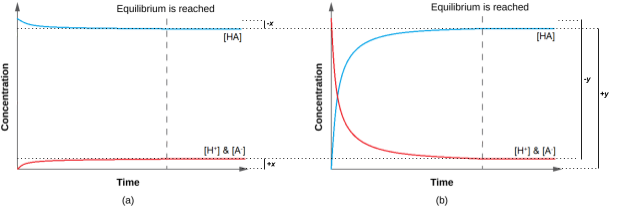
Figure 4.3.3. Regardless of wherever you start, whether it be with 100% reactants in (a) or 100% products in (b), we end up at the same equilibrium point regardless. (a) The change in the concentrations of reactants and products is depicted as the HA (aq) ⇌ H+ (aq) + A– (aq) reaction approaches equilibrium, when going from an “all reactant” starting point. (b) The change in concentrations of reactants and products is depicted as the reaction HA (aq) ⇌ H+ (aq) + A– (aq) approaches equilibrium, when going from an “all product” starting point.
Recall that a small value of K means that very little of the reactants form products and a large K means that most of the reactants form products. If the system can be arranged so it starts “close” to equilibrium, then if the change (x) is small compared to any initial concentrations, it can be neglected. The following two examples demonstrate this.
|
NOTE: |
|
For equilibrium problems in CHM1311, “x is small” is officially defined as resulting in an error of less than 5%. |
Example 4.3.7 – Approximate Solution Starting Close to Equilibrium
What are the concentrations at equilibrium of a 0.15 M solution of HCN?
HCN (aq) + H2O (l) ⇌ H3O+ (aq) + CN– (aq) K = 4.9 x 10-10
Solution
Using “x” to represent the concentration of each product at equilibrium gives this ICE table.
HCN (aq) + H2O (l) ⇌ H3O+ (aq) + CN– (aq)
| HCN (aq) | H2O (l) | H3O+ (aq) | CN– (aq) | |
| Initial Concentration (M) | 0.15 | ─ | 0 | 0 |
| Change (M) | -x | ─ | +x | +x |
| Equilibrium concentration (M) | 0.15 -x | ─ | +x | +x |
The exact solution may be obtained using the quadratic formula with
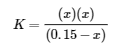
solving
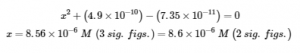
Thus [H3O+] = [CN–] = x = 8.6 × 10–6 M and [HCN] = 0.15 – x = 0.15 M.
In this case, chemical intuition can provide a simpler solution. From the equilibrium constant and the initial conditions, x must be small compared to 0.15 M. More formally, if x ≪ 0.15, then 0.15 – x ≈ 0.15 (Figure 4.3.4 visually demonstrates this).
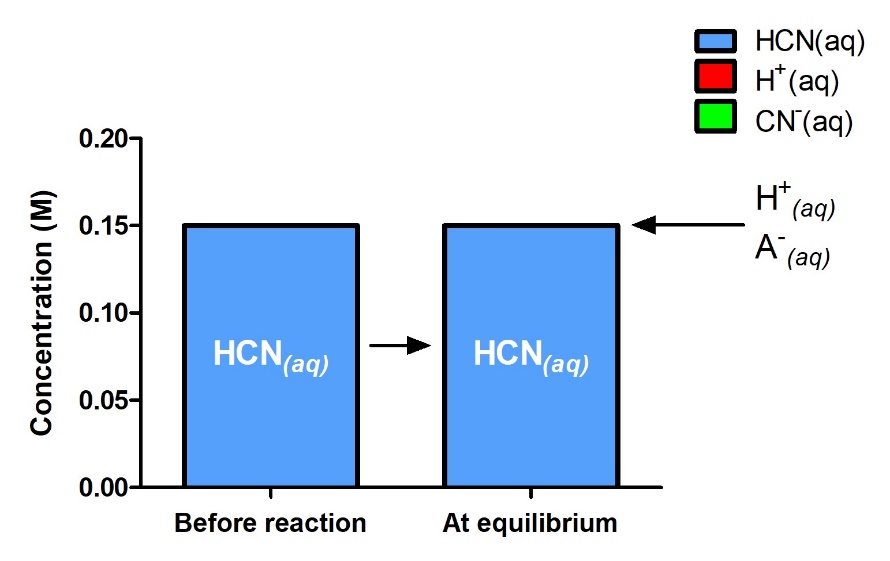
Figure 4.3.4. Concentrations of the reactant and products are shown initially and at equilibrium for the following reaction: HCN (aq) +H2O (l) ⇌ H3O+ (aq) + CN– (aq). The reaction starts with only HCN(aq), but even at equilibrium, you can tell that the relative amounts of H+ and CN– are so little that they are negligible – there is practically still only reagent which demonstrates the extremely small K value of the reaction and confirms the validity of the assumption that 0.15 – x ≈ 0.15.
If this assumption is true, then it simplifies obtaining x
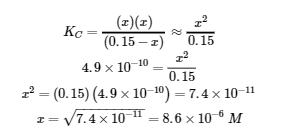
In this example, solving the exact (quadratic) equation and using approximations gave the same result to two significant figures. While most of the time the approximation is a bit different from the exact solution, as long as the error is less than 5%, the approximate solution is considered valid. In this problem, the 5% applies to (0.15 – x) ≈ 0.15 M, so if
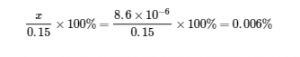
is less than 5%, as it is in this case, the assumption is valid. The approximate solution is thus a valid solution.
Check Your Learning 4.3.8 – Approximate Solution Starting Close to Equilibrium
What are the equilibrium concentrations in a 0.25 M NH3 solution?
NH3 (aq) + H2O (l) ⇌ NH4+ (aq) + OH– (aq) K = 1.8 x 10-5
Assume that x is much less than 0.25 M and calculate the error in your assumption.
Answer
[OH−] = [NH4+] = 0.0021 M; [NH3] = 0.25 M, error = 0.84%
|
|
The second example requires that the original information be processed a bit, but it still can be solved using a small x approximation.
Example 4.3.8 – Approximate Solution After Shifting Starting Concentration
Copper(II) ions form a complex ion in the presence of ammonia
If 0.010 mol Cu2+ is added to 1.00 L of a solution that is 1.00 M NH3 what are the concentrations when the system comes to equilibrium?
Solution:
The initial concentration of copper(II) is 0.010 M. The equilibrium constant is very large so it would be better to start with as much product as possible because “all products” is much closer to equilibrium than “all reactants” (Figure 4.3.5). Therefore, to simplify our calculations, let us assume that the reaction goes 100% to completion. Note that Cu2+ is the limiting reactant; if all 0.010 M of it reacts to form product the concentrations would
be
[Cu2+]= 0.010 – 0.010 = 0 M
[Cu(NH3)42+] = 0.010 M
[NH3] = 1.00 – 4 x 0.010 = 0.96 M
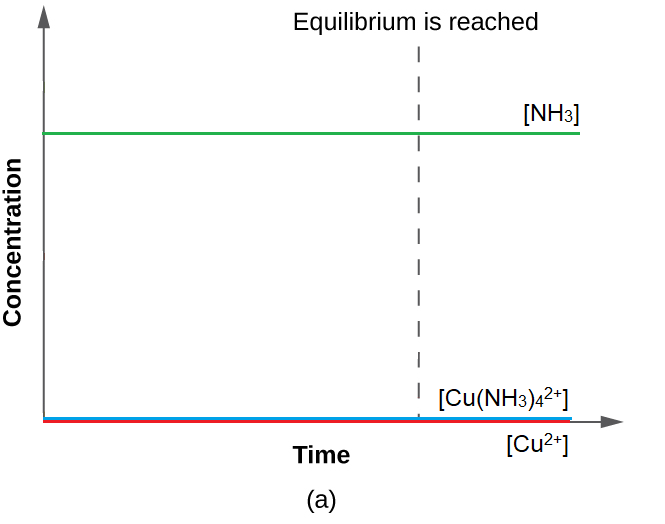
Figure 4.3.5. The K value is very large for the equilibrium reaction Cu2+(aq) + 4NH3(aq) ⇌ Cu(NH3)42+(aq), so products are very heavily favoured. The change in concentration of both products and reactants is almost minimal since as it stands, the relative concentration of all species initially almost already corresponds to the relative amounts at equilibrium, where the product is close to its maximum possible concentration.
Using these “shifted” values as initial concentrations with x as the free copper(II) ion concentration at equilibrium gives this ICE table.
Cu2+ (aq) +4NH3 (aq)⇌Cu(NH3)42+ (aq)
|
|
Cu2+ (aq) | 4NH3 (aq) | Cu(NH3)42+ (aq) |
| Initial Concentration (M) | 0 | 0.96 | 0.010 |
| Change (M) | +x | +4x | -x |
| Equilibrium concentration (M) | +x | 0.96 + 4x | 0.010 – x |
Since we are starting close to equilibrium, x should be small so that

Select the smallest concentration for the 5% rule – dividing a value by the smallest value possible will yield the largest possible error to really put the 5% rule to the test.
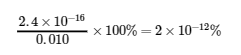
This is much less than 5%, so the assumptions are valid. The concentrations at equilibrium are
[Cu2+] = x = 2.4 x 10-16 M
[NH3] = 0.96 – 4x = 0.96 M
[Cu(NH3)42+] = 0.010 – x = 0.010 M
If we subtract x from 0.010 M, for example, we end up with 0.00999999… M which, when counting significant figures, rounds back up to 0.010 M anyway.
Overall, we started with a much higher concentration of reactant compared to product – note that we use up Cu2+ so initially we have the highest possible concentration of products. But since K is very large, the change in concentration is kept minimal since this reaction mixture almost practically corresponds to what is expected at equilibrium.
By starting with the maximum amount of product, this system was near equilibrium and the change (x) was very small – this very small change was particularly driven by the complete absence of Cu2+ initially (we discuss this in the context of Le Châtelier’s Principle in the next section). With only a small change required to get to equilibrium, the equation for x was greatly simplified and gave a valid result well within the 5% error maximum.
Check Your Learning 4.3.9 – Approximate Solution After Shifting Starting Concentration
What are the equilibrium concentrations when 0.25 mol Ni2+ is added to 1.00 L of 2.00 M NH3 solution?
Ni2+ (aq) + 6 NH3 (aq) ⇌ Ni(NH3)62+ (aq) KC = 5.5 x 108
With such a large equilibrium constant, first form as much product as possible, then assume that only a small amount (x) of the product shifts left. Calculate the error in your assumption.
Answer
[Ni(NH3)62+] = 0.25 M, [NH3] = 0.50 M, [Ni2+] = 2.9 × 10–8 M, error = 1.2 × 10–5 %
Questions
★ Questions
1. In the equilibrium reaction A + B ⇌ C, what happens to K if the concentrations of the reactants are doubled? tripled? Can the same be said about the equilibrium reaction A ⇌ B + C?
2. The following table shows the reported values of the equilibrium P{O2} at three temperatures for the reaction Ag2O (s) ⇌ 2 Ag (s) + 1/2 O2 (g) for which ΔH° = 31 kJ/mol. Are these data consistent with what you would expect to occur? Why or why not?
|
T (°C) |
P (O2) mm Hg |
|
150 |
182 |
|
184 |
143 |
|
191 |
126 |
3. Given the equilibrium system N2O4 (g) ⇌ 2 NO2 (g), what happens to KP if the initial pressure of N2O4 is doubled? If KP is 1.7 × 10−1 at 2300°C, and the system initially contains 100% N2O4 at a pressure of 2.6 × 102 bar, what is the equilibrium pressure of each component?
4. At 430°C, 4.20 mol of HI in a 9.60 L reaction vessel reaches equilibrium according to the following equation: H2 (g) + I2 (g) ⇌ 2 HI (g). At equilibrium, [H2] = 0.047 M and [HI] = 0.345 M. What are K and KP for this reaction?
5. Methanol, a liquid used as an automobile fuel additive, is commercially produced from carbon monoxide and hydrogen at 300°C according to the following reaction: CO (g) + 2 H2 (g) ⇌ CH3OH (g) and KP = 1.3 × 10−4. If 56.0 g of CO is mixed with excess hydrogen in a 250 mL flask at this temperature, and the hydrogen pressure is continuously maintained at 100 bar, what would be the maximum percent yield of methanol? What pressure of hydrogen would be required to obtain a minimum yield of methanol of 95% under these conditions?
★★ Questions
6. Starting with pure A, if the total equilibrium pressure is 0.969 atm for the reaction A (s) ⇌ 2 B (g) + C (g), what is KP (hint: must use the unit “bar” when working with KP)?
7. The decomposition of ammonium carbamate to NH3 and CO2 at 40°C is written as NH4CO2NH2 (s) ⇌ 2 NH3 (g) + CO2 If the partial pressure of NH3 at equilibrium is 0.242 atm, what is the equilibrium partial pressure (in atm) of CO2? What is the total gas pressure of the system (in atm)? What is KP(hint: must use the unit “bar” when working with Kp)?
8. At 375 K, KP for the reaction SO2Cl2 (g) ⇌ SO2 (g) + Cl2 (g) is 2.4, with pressures expressed in atmospheres. At 303 K, KP is 2.9 × 10−2.
a. What is K for the reaction at each temperature?
b. If a sample at 375 K has 0.100 M Cl2 and 0.200 M SO2 at equilibrium, what is the concentration of SO2Cl2?
c. If the sample given in part b is cooled to 303 K, what is the pressure inside the bulb (in atm)?
9. Experimental data on the system Br2 (l) ⇌ Br2 (aq) are given in the following table. Graph [Br2] versus moles of Br2 (l) present; then write the equilibrium constant expression and determine K.
|
Grams Br2 in 100 mL Water |
[Br2] (M) |
|
1.0 |
0.0626 |
|
2.5 |
0.156 |
|
3.0 |
0.188 |
|
4.0 |
0.219 |
|
4.5 |
0.219 |
10. Data accumulated for the reaction n-butane (g) ⇌ isobutane (g) at equilibrium are shown in the following table. What is the equilibrium constant for this conversion? If 1 mol of n-butane is allowed to equilibrate under the same reaction conditions, what is the final number of moles of n-butane and isobutane?

11. Solid ammonium carbamate (NH4CO2NH2) dissociates completely to ammonia and carbon dioxide when it vaporizes:
NH4CO2NH2 (s) ⇌ 2 NH3 (g) + CO2 (g)
At 25°C, the total pressure of the gases in equilibrium with the solid is 0.116 atm. What is the equilibrium partial pressure of each gas (in atm)? What is Kp(hint: must use the unit “bar” when working with KP)? If the concentration of CO2 is doubled and then equilibrates to its initial equilibrium partial pressure +x atm, what change in the NH3 concentration is necessary for the system to restore equilibrium?
12. The equilibrium constant for the reaction COCl2 (g) ⇌ CO (g) + Cl2 (g) is KP = 2.2 × 10−10 at 100°C. If the initial concentration of COCl2 is 3.05 × 10−3 M, what is the partial pressure of each gas at equilibrium at 100°C (in bar)? What assumption can be made to simplify your calculations?
13. Aqueous dilution of IO4− results in the following reaction:
IO4– (aq) + 2 H2O (l) ⇌ H4IO6– (aq)
and K = 3.5 × 10−2. If you begin with 50 mL of a 0.896 M solution of IO4− that is diluted to 250 mL with water, how many moles of H4IO6− are formed at equilibrium?
★★★ Questions
14. Iodine and bromine react to form IBr, which then sublimes. At 184.4°C, the overall reaction proceeds according to the following equation:
I2 (g) + Br2 (g) ⇌ 2 IBr (g)
KP = 1.2 × 102 (Hint: assumed to have used “bar” as a unit while calculating KP). If you begin the reaction with 7.4 g of I2 vapor and 6.3 g of Br2 vapor in a 1.00 L container, what is the concentration of IBr (g) at equilibrium (gmol-1)? What is the partial pressure of each gas at equilibrium (in bar)? What is the total pressure of the system (in bar)?
15. For the reaction
C (s) + 12 N2 (g) + 5/2 H2 (g) ⇌ CH3NH2 (g)
K = 1.8 × 10−6. If you begin the reaction with 1.0 mol of N2, 2.0 mol of H2, and sufficient C(s) in a 2.00 L container, what are the concentrations of N2 and CH3NH2 at equilibrium (gmol-1)? What happens to K if the concentration of H2 is doubled?
Answers
1. The K value is now raised to the respected factor. When it is doubled K is now K2 and when it is tripled, K is K3
2. These results are not expected, as with an increase in temperature an increase in pressure should occur. ∆H० is a positive value in this case (31 kJ/mol) indicating that it is an endothermic reaction. This being said, with an increase in temperature the reaction will shift forward meaning that more product will be produced. If more product is produced, more oxygen gas is present, therefore increasing its pressure.
3. Kp would remain the same, PN2O2 = 2.3 x 102 bar, PNO2 = 6.6 bar
4. K = 53.88; Kp = 53.88
5. 215 bar MeOH; 383 bar H2
6. Kp = 0.140
7. Partial Pressure of CO2 = 0.121 atm; total gas pressure of the system = 0.363 atm; Kp = 7.37 x 10-3
8. (a) K = 7.8 x 10-2 at 375K, K = 1.2 x 10-3 at 303K ; (b) 0.256 M; (c) 14.13 atm
9.
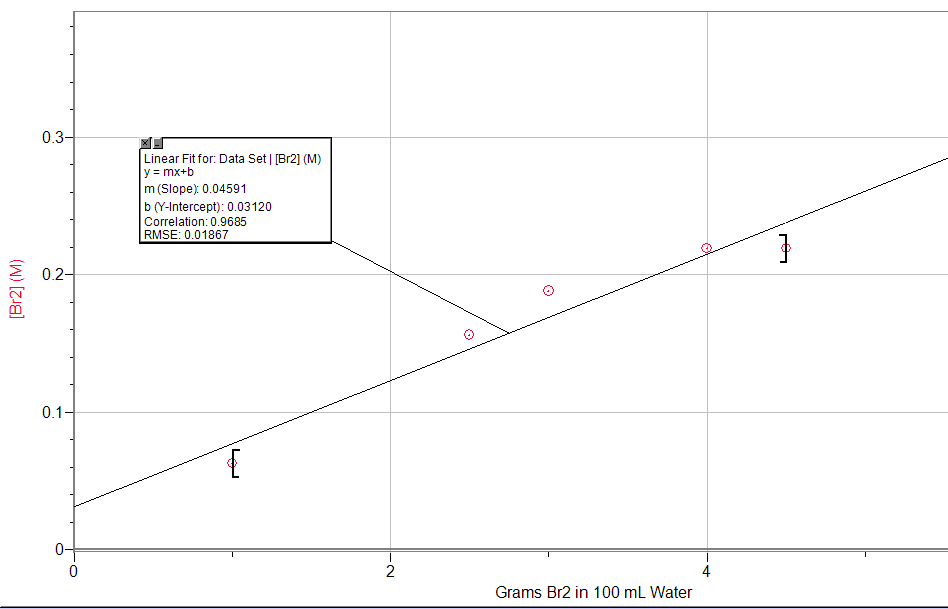 K = 0.046 (based on the slope of the line of best fit)
K = 0.046 (based on the slope of the line of best fit)
10. K = 2.5; the final moles will be 0.3 mol of n-butane and 0.7 mol of isobutane.
11. PNH3= 0.0773 atm, PCO2 = 0.0387 atm; Kp = 2.411 x 10-4; the concentration of NH3 will drop in order for the equilibrium to restore.
12. PCOCl2 = 0.042 bar, PCO = 4.59 x 10-6 bar, PCl2 = 4.59 x 10-6 bar; An assumption to be made is that the total volume is 1L.
13. H4IO6– = 9.09 x 10-3 mol
14. PI2 = 7.7 bar, PBr2 = 47 bar, PIBr = 2.1 x102 bar = 0.054 M, PT = 2.6 x 102 bar
15. [N2] ≈ 0.99 M, [H2] ≈ 2 M, [CH3NH2] = 1.02 x 10-5 M; if the [H2] doubles, K remains unchanged (only temperature can alter a K value)

 W
W