5.6 – Lewis Acids & Bases

Note: The Brønsted-Lowry Theory is sufficiently accurate enough to cover the acid-base concepts introduced in CHM1311. However, in the context of organic chemistry, the Lewis Theory of acid-base behaviour is much more appropriate, and thus it will be further discussed in detail in CHM 1321. The description of the theory is included here for completion, as supplementary material.

In 1923, G. N. Lewis proposed a generalized definition of acid-base behavior in which acids and bases are identified by their ability to accept or to donate a pair of electrons and form a coordinate covalent bond.

A coordinate covalent bond (or dative bond) occurs when one of the atoms in the bond provides both bonding electrons. For example, a coordinate covalent bond occurs when a water molecule combines with a proton to form a hydronium ion. A coordinate covalent bond also results when an ammonia molecule combines with a proton to form an ammonium ion. Both of these equations are shown here, with the coordinate covalent bonds consisting of two electrons each indicated in red.

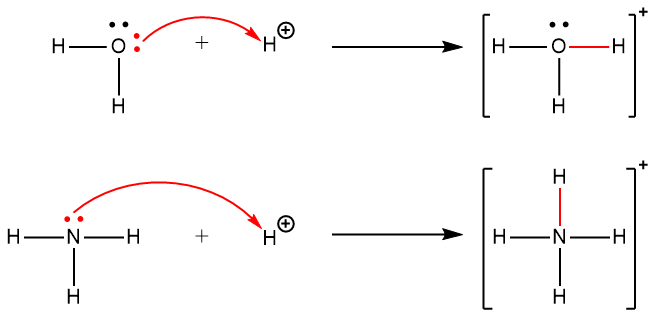
Reactions involving the formation of coordinate covalent bonds are classified as Lewis acid-base chemistry.

A Lewis acid is any species (molecule or ion) that can accept a pair of electrons, and a Lewis base is any species (molecule or ion) that can donate a pair of electrons.

A Lewis acid-base reaction occurs when a base donates a pair of electrons to an acid. In many Lewis acid-base reactions, a Lewis acid-base adduct, a compound that contains a coordinate covalent bond between the Lewis acid and the Lewis base, is formed.

Example 5.6.1 – Identifying Lewis Acids & Bases

Identify the acid and the base in each Lewis acid–base reaction.

(a) BH₃ + (CH₃)₂S → H₃B:S(CH₃)₂

(b) CaO + CO₂ → CaCO₃

(c) BeCl₂ + 2 Cl⁻ → BeCl₄²⁻

Solution

(a) In BH₃, boron has only six valence electrons. It is therefore electron deficient and can accept a lone pair. Like oxygen, the sulfur atom in (CH₃)₂S has two lone pairs. Thus (CH₃)₂S donates an electron pair on sulfur to the boron atom of BH₃. The Lewis base is (CH₃)₂S, and the Lewis acid is BH₃.

(b) The oxygen in CaO is an electron-pair donor, so CaO is the Lewis base. Carbon accepts a pair of electrons, so CO₂ is the Lewis acid.

(c) The chloride ion contains four lone pairs. In this reaction, each chloride ion donates one lone pair to BeCl₂, which has only four electrons around Be. Thus the chloride ions are Lewis bases, and BeCl₂ is the Lewis acid.

Check Your Learning 5.6.1 – Identifying Lewis Acids & Bases

Identify the acid and the base in each Lewis acid–base reaction.

(a) (CH₃)₂O + BF₃ → (CH₃)₂O:BF₃

(b) H₂O + SO₃ → H₂SO₄

Answer

(a) Lewis base: (CH₃)₂O; Lewis acid: BF₃; (b) Lewis base: H₂O; Lewis acid: SO₃

The following equations illustrate the general application of the Lewis concept and Lewis structures. Lewis Structures are covered in detail in the section on molecular bonding, Section 9.1, but for now, all you need to know is that atoms are indicated by their elemental symbol, with the lines connecting them within molecules representing covalent bonds. The dots surrounding the elemental symbols represent lone pairs of electrons – we’ll visually display the dative bonds and the electrons that form them with a red colour to assist you with your understanding.

The boron atom in boron trifluoride, BF₃, has only six electrons in its valence shell. Since the boron atom has an incomplete octet, it can behave as an electron pair acceptor. As a result, BF₃ is a very good Lewis acid and reacts with many Lewis bases; a fluoride ion is the Lewis base in this reaction, donating one of its lone pairs:

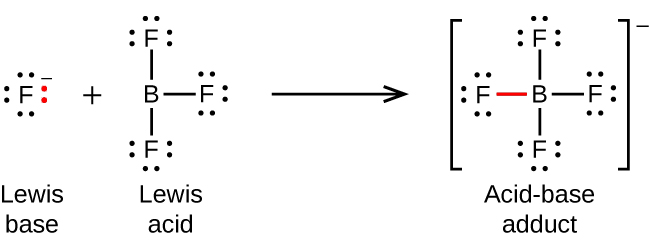
Note the negative charge on the adduct – since the sum of charges on the left hand side of the equation is -1, the sum of charges on the right hand side must also be -1.

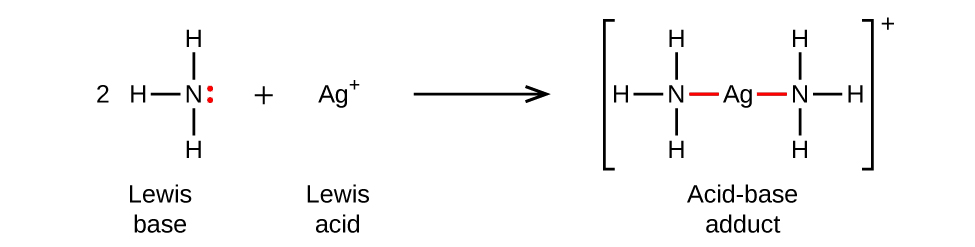
In the following reaction, each of two ammonia molecules, Lewis bases, donates a pair of electrons to a positively charged silver ion, the Lewis acid. Note once again that the sum of charges on the left side is +1, so the acid-base adduct on the right hand side must carry a charge of +1:

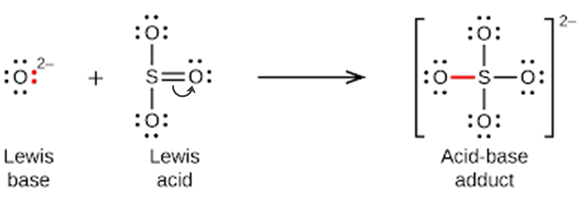
Nonmetal oxides act as Lewis acids and react with oxide ions, Lewis bases, to form oxyanions:

Many Lewis acid-base reactions are displacement reactions in which one Lewis base displaces another Lewis base from an acid-base adduct, or in which one Lewis acid displaces another Lewis acid:

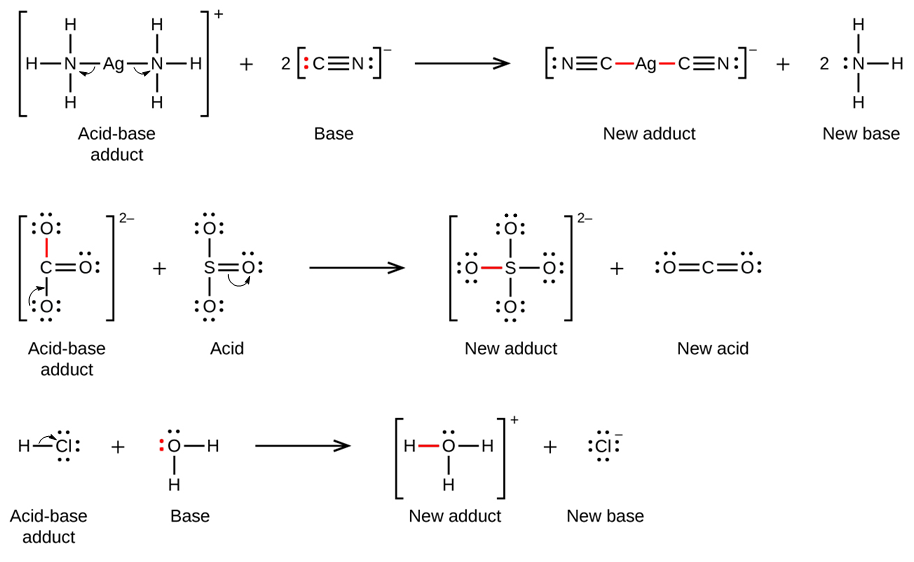
The last displacement reaction shows how the reaction of a Brønsted-Lowry acid with a base fits into the Lewis concept. A Brønsted-Lowry acid such as HCl is an acid-base adduct according to the Lewis concept, and proton transfer occurs because a more stable acid-base adduct is formed. Thus, although the definitions of acids and bases in the two theories are quite different, the theories overlap considerably.

Many slightly soluble ionic solids dissolve when the concentration of the metal ion in solution is decreased through the formation of complex (polyatomic) ions in a Lewis acid-base reaction. For example, silver chloride dissolves in a solution of ammonia because the silver ion reacts with ammonia to form the complex ion Ag(NH₃)₂⁺. The Lewis structure of the Ag(NH₃)₂⁺ ion is: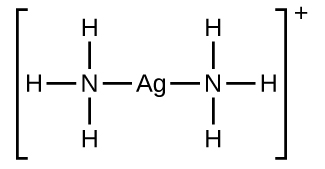

The equations for the dissolution of AgCl in an aqueous solution of NH₃ are:

AgCl (s) ⇌ Ag⁺ (aq) + Cl⁻ (aq)

Ag⁺ (aq) + 2NH₃ (aq) ⇌ Ag(NH₃)₂⁺ (aq)

Sum: AgCl (s) + Ag⁺ (aq) + 2NH₃ (aq) ⇌ Ag(NH₃)₂⁺ (aq) + Ag⁺ (aq) + Cl⁻ (aq)

Net: AgCl (s) + 2NH₃ (aq) ⇌ Ag(NH₃)₂⁺ (aq) + Cl⁻ (aq)

Aluminum hydroxide dissolves in a solution of sodium hydroxide or another strong base because of the formation of the complex ion Al(OH)⁴⁻. The Lewis structure of the Al(OH)⁴⁻ ion is:

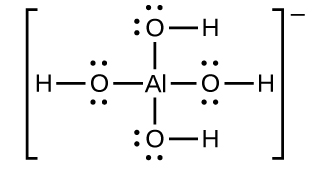
The equations for the dissolution are:

Al(OH)₃ (s) ⇌ Al³⁺ (aq) + 3OH^– (aq)

Al³⁺ (aq) + 4OH^– (aq) ⇌ Al(OH)₄^– (aq)

Sum: Al(OH)₃ (s) + Al³⁺ (aq) + 4 OH^– (aq)  ⇌ Al(OH)₄^– (aq) + Al³⁺ (aq) + 3OH^– (aq)

Net: Al(OH)₃ (s) + OH^– (aq) ⇌ Al(OH)₄^– (aq)

Mercury(II) sulfide dissolves in a solution of sodium sulfide because HgS reacts with the S^2– ion:

HgS (s) ⇌ Hg²⁺ (aq) + S^2- (aq)

Hg²⁺ (aq) + 2S^2- (aq) ⇌ HgS₂^2- (aq)

Sum: HgS (s) + 2 S^2- (aq) + Hg²⁺ ⇌ HgS₂^2- (aq) + S^2- (aq) + Hg²⁺

Net: HgS (s) + S^2- (aq) ⇌ HgS₂^2- (aq)

A complex ion consists of a central atom, typically a transition metal cation, surrounded by ions, or molecules called ligands. These ligands can be neutral molecules like H₂O or NH₃, or ions such as CN^– or OH^–. Usually, the ligands act as Lewis bases, donating a pair of electrons to the central atom. The ligands form bonds with the central atom or ion, creating a new ion with a charge equal to the sum of the charges of the ligands and the central atom or ion. This more complex arrangement is why the resulting ion is called a complex ion. The complex ion formed in these reactions cannot be predicted; it must be determined experimentally. The types of bonds formed in complex ions are coordinate covalent bonds, as electrons from the ligands are being shared with the central atom. Because of this, complex ions are sometimes referred to as coordination complexes.

The equilibrium constant for the reaction of the components of a complex ion to form the complex ion in solution is called a formation constant (K_f) (sometimes called a stability constant). For example, the complex ion Cu(CN)₂⁻ is shown here:

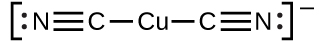
It forms by the reaction:

Cu⁺ (aq) + 2CN^– (aq) ⇌ Cu(CN)₂^– (aq)

At equilibrium:

K_f=[Cu(CN)^2-]/([Cu⁺][CN^–]²)

The inverse of the formation constant is the dissociation constant (K_d), the equilibrium constant for the decomposition of a complex ion into its components in solution. Appendix J and Table 5.6.1 show a range of formation constants. In general, the larger the formation constant, the more stable the complex.

Table 5.6.1. Common Complex Ions and their Formation Constants

As an example of dissolution by complex ion formation, let us consider what happens when we add aqueous ammonia to a mixture of silver chloride and water. Silver chloride dissolves slightly in water, giving a small concentration of Ag⁺ ([Ag⁺] = 1.3 × 10^–5 M):

AgCl (s) ⇌ Ag⁺ (aq) + Cl^– (aq)

However, if NH₃ is present in the water, the complex ion, Ag(NH₃)₂⁺, can form according to the equation:

Ag⁺ (aq) + 2NH₃ (aq) ⇌ Ag(NH₃)₂⁺ (aq)

with

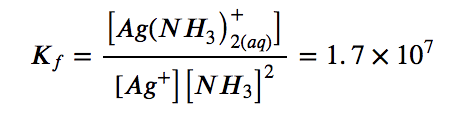
The large size of this formation constant indicates that most of the free silver ions produced by the dissolution of AgCl combine with NH₃ to form Ag(NH₃)₂⁺. As a consequence, the concentration of silver ions, [Ag⁺], is reduced, and the reaction quotient for the dissolution of silver chloride, [Ag⁺][Cl^–], falls below the solubility product of AgCl:

Q=[Ag⁺][Cl^–]<K_sp

More silver chloride then dissolves. If the concentration of ammonia is great enough, all of the silver chloride dissolves. Solubility and Ksp are discussed in greater detail in Section 6.4.

Example 5.6.2 – Dissociation of a Complex Ion

Calculate the concentration of the silver ion in a solution that is initially 0.10 M Ag(NH₃)₂⁺.

Solution

We use the familiar path to solve this problem:

1. Determine the direction of change. The complex ion Ag(NH₃)₂⁺ is in equilibrium with its components, as represented by the equation:

Ag⁺ (aq) + 2NH₃ (aq) ⇌ Ag(NH₃)₂⁺ (aq)  K_f = 1.7 × 10⁷

We write the equilibrium as a formation reaction because Appendix J lists formation constants for complex ions. Initially, only the complex ion is present ([Ag⁺] = 0 and [NH₃] = 0), Q > K_f, and so the reaction shifts to the left (towards reactants) to reach equilibrium.

2. Determine x and equilibrium concentrations. We let the change in concentration of Ag⁺ be x. Dissociation of 1 mol of Ag(NH₃)₂⁺ gives 1 mol of Ag⁺ and 2 mol of NH₃, so the change in [NH₃] is 2x and that of Ag(NH₃)₂⁺ is  –x. In summary:

Ag⁺ + 2NH₃⇌ Ag(NH₃)₂⁺

3. Solve for x and the equilibrium concentrations. At equilibrium:

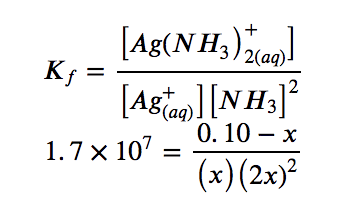
Since K_f is very large, we know that this is a heavily product-favoured reaction, and therefore very little of the complex will dissociate into the separate ions. Therefore, let us assume that the changes in concentrations needed to reach equilibrium are small. Thus 0.10 – x is approximated as 0.10 to simplify our calculations:

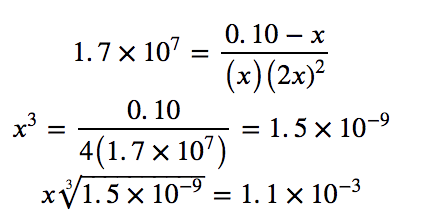
Checking the assumption we made, we find that only 1.1% of the Ag(NH₃)₂⁺ dissociates into Ag⁺ and NH₃, and therefore the assumption that x is small is justified.

Now we determine the equilibrium concentrations:

[Ag+]=0+x=1.1×10^-3 M

[NH₃]=0+2x=2.2×10^-3 M

[Ag(NH₃)₂⁺]=0.10-x=0.10-0.0011=0.099

The concentration of free silver ion in the solution is 0.0011 M.

4. Check the work. The value of Q calculated using the equilibrium concentrations is equal to K_f within the error associated with the significant figures in the calculation.

Check Your Learning 5.6.2 – Dissociation of a Complex Ion

Calculate the silver ion concentration, [Ag⁺], of a solution prepared by dissolving 1.00 g of AgNO₃ and 10.0 g of KCN in sufficient water to make 1.00 L of solution. (Hint: Because Q < K_f, assume the reaction goes to completion then calculate the [Ag⁺] produced by dissociation of the complex.)

Answer

2.5 × 10^–22 M

Questions

★ Questions

1. Under what circumstances, if any, does a sample of solid AgCl completely dissolve in pure water?
2. Explain why the addition of NH₃ or HNO₃ to a saturated solution of Ag₂CO₃ in contact with solid Ag₂CO₃ increases the solubility of the solid.
3. Calculate the cadmium ion concentration (g⋅mol^-1), [Cd²⁺], in a solution prepared by mixing 0.100 L of 0.0100 M Cd(NO₃)₂ with 1.150 L of 0.100 M NH₃(aq).
4. Explain why addition of NH₃ or HNO₃ to a saturated solution of Cu(OH)₂ in contact with solid Cu(OH)₂ increases the solubility of the solid.
5. Sometimes equilibria for complex ions are described in terms of dissociation constants, K_d. For the complex ion AlF₆³⁻ the dissociation reaction is:

AlF₆^3- ⇌ Al³⁺ + 6F^– and K_d=([Al³⁺][F^–]⁶)/[AlF₆^3-]=2×10^-24

6. Using the dissociation constant, K_d = 7.8 × 10^–18, calculate the equilibrium concentrations (g⋅mol^-1) of Cd²⁺ and CN^– in a 0.250 M solution of Cd(CN)₄²⁻.

7. Using the dissociation constant, K_d = 2.2 × 10^–34, calculate the equilibrium concentrations (g⋅mol^-1) of Co³⁺ and NH₃ in a 0.500 M solution of Co(NH₃)₆³⁺.

8. Calculate the mass of potassium cyanide ion (in grams) that must be added to 100 mL of solution to dissolve 2.0 × 10^–2 mol of silver cyanide, AgCN.

★★ Questions

9. A roll of 35 mm black and white photographic film contains about 0.27 g of unexposed AgBr before developing. What mass (in grams) of Na₂S₂O₃·5H₂O (sodium thiosulfate pentahydrate or hypo) in 1.0 L of developer is required to dissolve the AgBr as Ag(S₂O₃)₂³⁻ (K_f = 4.7 × 10¹³)?

10. We have seen an introductory definition of an acid: An acid is a compound that reacts with water and increases the amount of hydronium ion present. In the chapter on acids and bases, we saw two more definitions of acids: a compound that donates a proton (a hydrogen ion, H⁺) to another compound is called a Brønsted-Lowry acid, and a Lewis acid is any species that can accept a pair of electrons. Explain why the introductory definition is a macroscopic definition, while the Brønsted-Lowry definition and the Lewis definition are microscopic definitions.

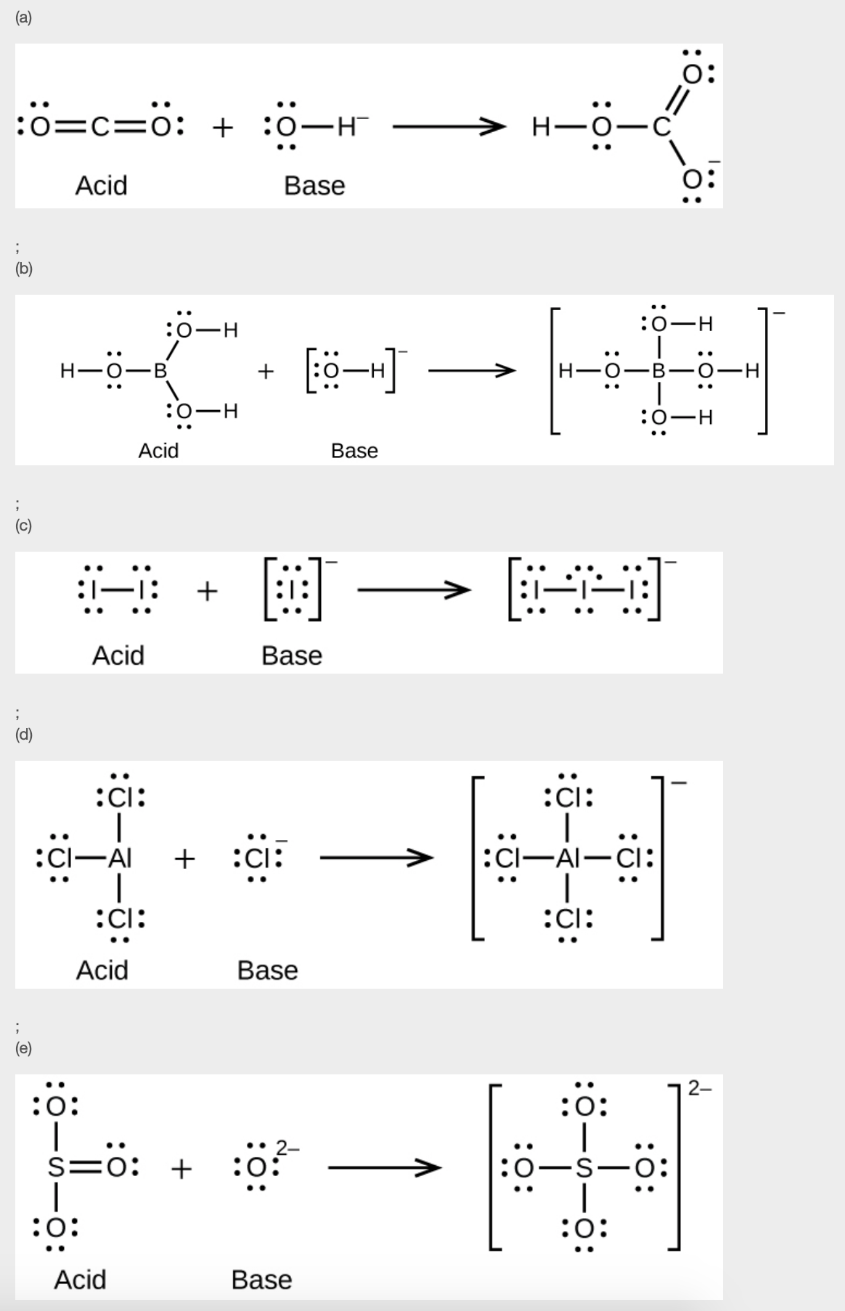
11. Write the Lewis structures of the reactants and product of each of the following equations, and identify the Lewis acid and the Lewis base in each:

(a) CO₂ + OH^– → HCO₃^–

(b) B(OH)₃ + OH^– → B(OH)₄^–

(c) I^– + I₂ → I₃^–

(d) AlCl₃ + Cl^– → AlCl₄^– (use Al – Cl single bonds)

(e) O^2- + SO₃ → SO₄^2-

12. Write the Lewis structures of the reactants and product of each of the following equations, and identify the Lewis acid and the Lewis base in each:

(a) CS₂ + SH^– → HCS₃^–

(b) BF₃ + F^– → BF₄^–

(c) I^– + SnI₂ → SnI₃^–

(d) Al(OH)₃ + OH^– → Al(OH)₄^–

(e) F^– + SO₃ → SFO₃^–

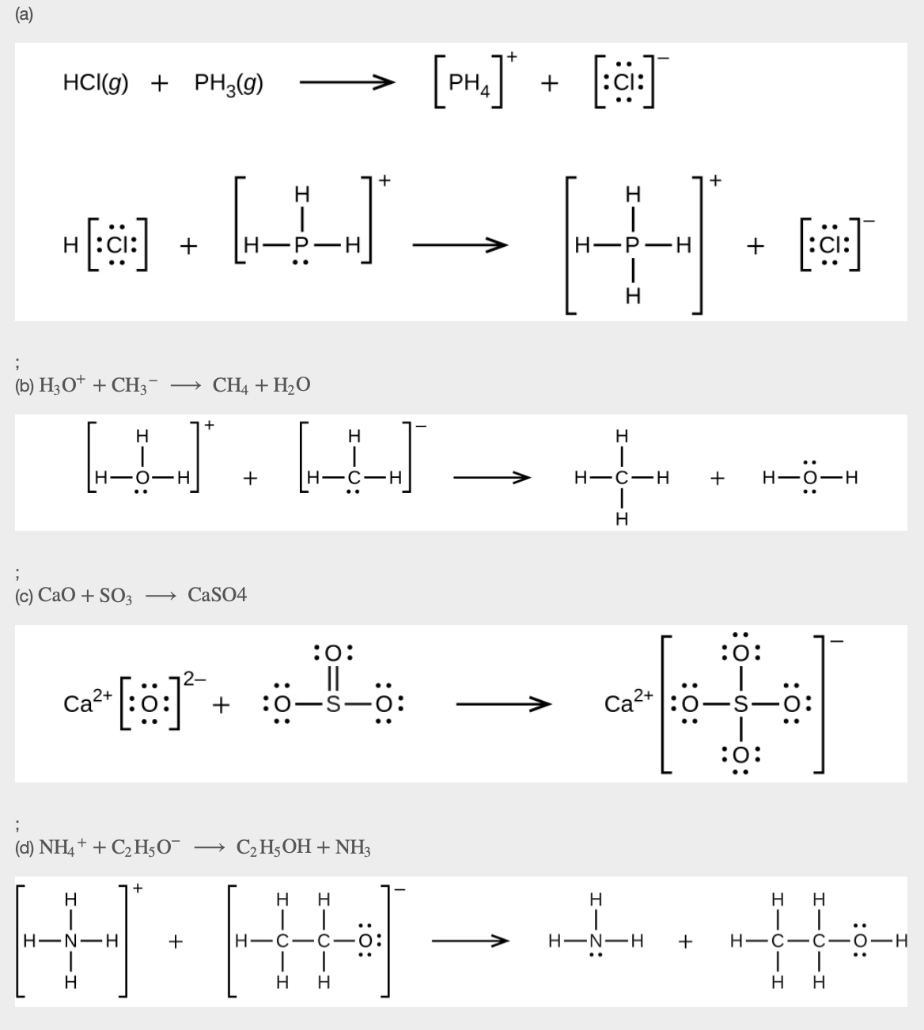
13. Using Lewis structures, write balanced equations for the following reactions:

(a) HCl (g) + PH₃ (g) →

(b) H₃O⁺ + CH₃^– →

(c) CaO + SO₃ →

(d) NH₄⁺ + C₂H₅O^– →

14. In a titration of cyanide ion, 28.72 mL of 0.0100 M AgNO₃ is added before precipitation begins. [The reaction of Ag⁺ with CN–goes to completion, producing the Ag(CN)₂⁻ complex.] Precipitation of solid AgCN takes place when excess Ag⁺ is added to the solution, above the amount needed to complete the formation of Ag(CN)₂⁻. How many grams (mass) of NaCN were in the original sample?

15. In dilute aqueous solution HF acts as a weak acid. However, pure liquid HF (boiling point = 19.5 °C) is a strong acid. In liquid HF, HNO₃ acts like a base and accepts protons. The acidity of liquid HF can be increased by adding one of several inorganic fluorides that are Lewis acids and accept F^– ion (for example, BF₃ or SbF₅). Write balanced chemical equations for the reaction of pure HNO₃ with pure HF and of pure HF with BF₃.

16. Boric acid, H₃BO₃, is not a Brønsted-Lowry acid but a Lewis acid.

(a) Write an equation for its reaction with water.

(b) Predict the shape of the anion thus formed.

(c) What is the hybridization on the boron consistent with the shape you have predicted?

Answers

1. When the amount of solid is so small that a saturated solution is not produced.
2. CO₃ is a conjugate base of a weak acid meaning it hydrolyzes pushing the equilibrium to the right, therefore increasing solubility.
3. 8 × 10^–5 M
4. OH- is removed from the solution by reacting with either NH₃ or HNO₃ pushing the equilibrium to the right, therefore increasing solubility.
5. 5 × 10²³
6. [Cd(CN)₄^2-] + [CN^–]⇌ [Cd²⁺]

7. [Co₃⁺] = 3.0 × 10–6 M; [NH₃] = 1.8 × 10^–5 M

8. 1.3 g

9. 0.79 g

10. Since almost all acids (whether Lewis or Brønsted-Lowry) increase the concentration of hydronium in the solution by reacting with water, the introductory definition of acids encompasses the behaviour of such compounds, and is therefore a macroscopic definition of an acid. Since the Lewis or Brønsted-Lowry definitions explain the mechanisms behind the (i.e Brønsted-Lowry acids release H⁺) hydronium ion concentration increase, they are considered a microscopic definition.

11.

12.

(a)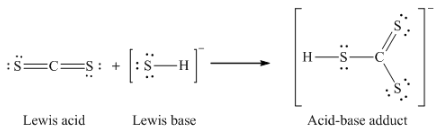

(b)

(c)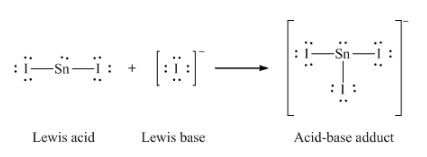

(d)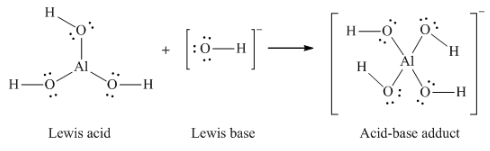

(e)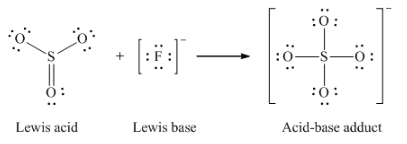

13.

14. 0.0281 g

15. HNO₃ (l) + HF (l) → H₂NO₃⁺ + F^– ; HF (l) + BF₃ (g) → H⁺ + BF₄

16. (a) H₃BO₃ + H₂O → H₄BO₄^– + H⁺ ; (b) The electronic and molecular shapes are the same – both tetrahedral. (c) The tetrahedral structure is consistent with sp³ hybridization.