3.5 – Calorimetry

One technique we can use to measure the amount of heat involved in a chemical or physical process is known as calorimetry. Calorimetry is used to measure amounts of heat transferred to or from a substance. To do so, the heat is exchanged with a calibrated object (calorimeter). The temperature change measured by the calorimeter is used to derive the amount of heat transferred by the process under study. The measurement of heat transfer using this approach requires knowledge and understanding of a system and its surroundings (see “Introduction to Thermochemistry” to review the terminology of system and surroundings). As we saw in previous sections, energy in the universe is neither created nor destroyed, only transferred. This implies that the change in internal energy of the universe must be zero – it is all conserved where there is no gain of energy or loss of it:

ΔU_universe = 0

In addition to this, we also need to understand a few other concepts that we’ll go over in this section to grasp the concept of calorimetry.

Heat Capacities

We now introduce two concepts useful in describing heat flow and temperature change. The heat capacity (C) of a body of matter is the quantity of heat (q) it absorbs or releases when it experiences a temperature change (ΔT) of 1 degree Celsius (or equivalently, 1 kelvin):

C = q/ΔT

Equation 3.5.1 Heat Capacity

Heat capacity is determined by both the type and amount of substance that absorbs or releases heat. It is therefore an extensive property—its value is proportional to the amount of the substance.

For example, consider the heat capacities of two cast iron frying pans. The heat capacity of the large pan is five times greater than that of the small pan because, although both are made of the same material, the mass of the large pan is five times greater than the mass of the small pan. More mass means more atoms are present in the larger pan, so it takes more energy to make all of those atoms vibrate faster. The heat capacity of the small cast iron frying pan is found by observing that it takes 18 150 J of energy to raise the temperature of the pan by 50.0 °C: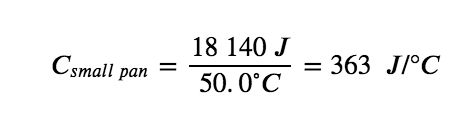  

The larger cast iron frying pan, while made of the same substance, requires 90,700 J of energy to raise its temperature by 50.0 °C. The larger pan has a (proportionally) larger heat capacity because the larger amount of material requires a (proportionally) larger amount of energy to yield the same temperature change:

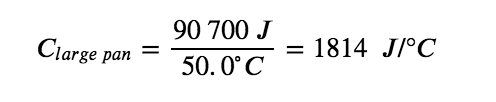
The specific heat capacity (c) of a substance, commonly called its “specific heat,” is the quantity of heat required to raise the temperature of 1 gram of a substance by 1 degree Celsius (or 1 kelvin):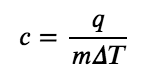

Equation 3.5.2 Specific Heat Capacity 

Note the important difference in units between C and c: the heat capacity, C, is expressed in energy per temperature change, whereas the specific heat capacity, c, is expressed in energy per temperature change as well, but this time per mass. In other words, the specific heat capacity takes it a step further by taking mass into account.

Specific heat capacity depends only on the kind of substance absorbing or releasing heat. It is an intensive property—the type, but not the amount, of the substance is all that matters. For example, the small cast iron frying pan has a mass of 808 g. The specific heat of iron (the material used to make the pan) is, therefore: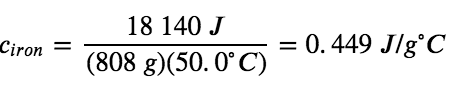 

The large frying pan has a mass of 4040 g. Using the data for this pan, we can also calculate the specific heat of iron:

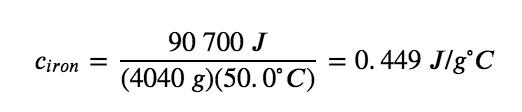
Although the large pan is more massive than the small pan, since both are made of the same material, they both yield the same value for specific heat (for the material of construction, iron). Note that specific heat is measured in units of energy per temperature per mass and is an intensive property, being derived from a ratio of two extensive properties (heat and mass). The molar heat capacity, also an intensive property, is the heat capacity per mole of a particular substance and has units of J/mol °C (Figure 3.5.1).

In real-life applications, we typically use C for larger-scale applications like objects where the exact mass isn’t important and differences in mass can be seen qualitatively (object is larger, feels significantly heavier), or when working with different-sized objects of the same composition. The specific heat capacity, c, applies to more smaller-scale applications like substances where the mass becomes something important to consider to meet specific requirements (e.g. determining the most appropriate mass of NH₄NO₃ to use in an ice pack that is convenient in terms of mass and delivers a temperature change that is just right).

Figure 3.5.1. Due to its larger mass, a large frying pan has a larger heat capacity than a small frying pan. Because they are made of the same material, both frying pans have the same specific heat. (credit: Mark Blaser)

Liquid water has a relatively high specific heat (about 4.2 J/g °C); most metals have much lower specific heats (usually less than 1 J/g °C). The specific heat of a substance varies somewhat with temperature. However, this variation is usually small enough that we will treat specific heat as constant over the range of temperatures that will be considered in this chapter. Specific heats of some common substances are listed in the table below.

* CRC Handbook of Chemistry and Physics 100th Edition (Online) (Electronic ed.). (2019). Boca Raton, Fla: CRC Press.

Table 3.5.1 Specific Heats of Common Substances at 25°C and 1 bar*

If we know the mass of a substance and its specific heat, we can determine the amount of heat, q, entering or leaving the substance by measuring the temperature change before and after the heat is gained or lost:

q = (specific heat) × (mass of substance) × (temperature change)

q = c × m × ΔT = c × m × (T_final – T_initial)

In this equation, c is the specific heat of the substance, m is its mass, and ΔT (which is read “delta T”) is the temperature change, T_final − T_initial. Since c and m are both always positive values, the only variable that determines whether heat is absorbed or released is the temperature change. If a substance gains thermal energy, its temperature increases, its final temperature is higher than its initial temperature, T_final − T_initial has a positive value, and the value of q is positive. If a substance loses thermal energy, its temperature decreases, the final temperature is lower than the initial temperature, T_final − T_initial has a negative value, and the value of q is negative. If you try the math out using the equation q = mcΔT, you’ll see that this reasoning checks out:

Example 3.5.1 – Measuring Heat

A flask containing 8.0 × 10² g of water is heated, and the temperature of the water increases from 21 °C to 85 °C. How much heat did the water absorb?

Solution

To answer this question, consider these factors:

• • • the specific heat of the substance being heated (in this case, water)
    • the amount of substance being heated (in this case, 8.0 × 10² g)
    • the magnitude of the temperature change (in this case, from 21 °C to 85 °C).

The specific heat of water is 4.184 J/g °C, so to heat 1 g of water by 1 °C requires 4.184 J. We note that since 4.184 J is required to heat 1 g of water by 1 °C, we will need 800 times as much to heat 8.0 × 10² g of water by 1 °C. Finally, we observe that since 4.184 J is required to heat 1 g of water by 1 °C, we will need 64 times as much to heat it by 64 °C (that is, from 21 °C to 85 °C).

This can be summarized using the equation:

q = c × m × ΔT = c × m × (T_final – T_initial)

=(4.184 J/g∘C) × (8.0 × 10² g) × (85 – 21)∘C

=(4.184 J/g∘C) × (8.0 × 10² g) × (64)∘C

=210,000 J  (= 2.1 × 10² kJ)

Because the temperature increased, the water absorbed heat and q is positive.

Check Your Learning 3.5.1 – Measuring Heat

How much heat, in joules, must be added to a 5.07 × 10⁴ J iron skillet to increase its temperature from 25 °C to 250 °C? The specific heat of iron is 0.449 J/g °C.

Answer

5.07 × 10⁴ J

Note that the relationship between heat, specific heat, mass, and temperature change can be used to determine any of these quantities (not just heat) if the other three are known or can be deduced.

Example 3.5.2 – Determining Other Quantities

A piece of unknown metal weighs 348 g. When the metal piece absorbs 6.64 kJ of heat, its temperature increases from 22.4°C to 43.6°C. Determine the specific heat of this metal (which might provide a clue to its identity).

Solution

Since mass, heat, and temperature change are known for this metal, we can determine its specific heat using the relationship:

q = c × m × ΔT = c × m × (T_final – T_initial)

Substituting the known values:

6640 J = c × (348 g) × (43.6 – 22.4)∘C

Solving:

Comparing this value with the values in the table for specific heats of common substances (at 25°C & 1 bar), this value matches the specific heat of aluminum, which suggests that the unknown metal is aluminum.

Check Your Learning 3.5.2 – Determining Other Quantities

A piece of unknown metal weighs 217 g. When the metal piece absorbs 1.43 kJ of heat, its temperature increases from 24.5 °C to 39.1 °C. Determine the specific heat of this metal, and predict its identity.

Answer:

c = 0.451 J/g °C; the metal is likely to be iron

Measuring Heat Flow – Calorimeters

A calorimeter is a device used to measure the amount of heat involved in a chemical or physical process. For example, when an exothermic reaction occurs in solution in a calorimeter, the heat produced by the reaction is absorbed by the solution, which increases its temperature. When an endothermic reaction occurs, the heat required is absorbed from the thermal energy of the solution, which decreases its temperature (Figure 3.5.2). The temperature change, along with the specific heat and mass of the solution, can then be used to calculate the amount of heat involved in either case.

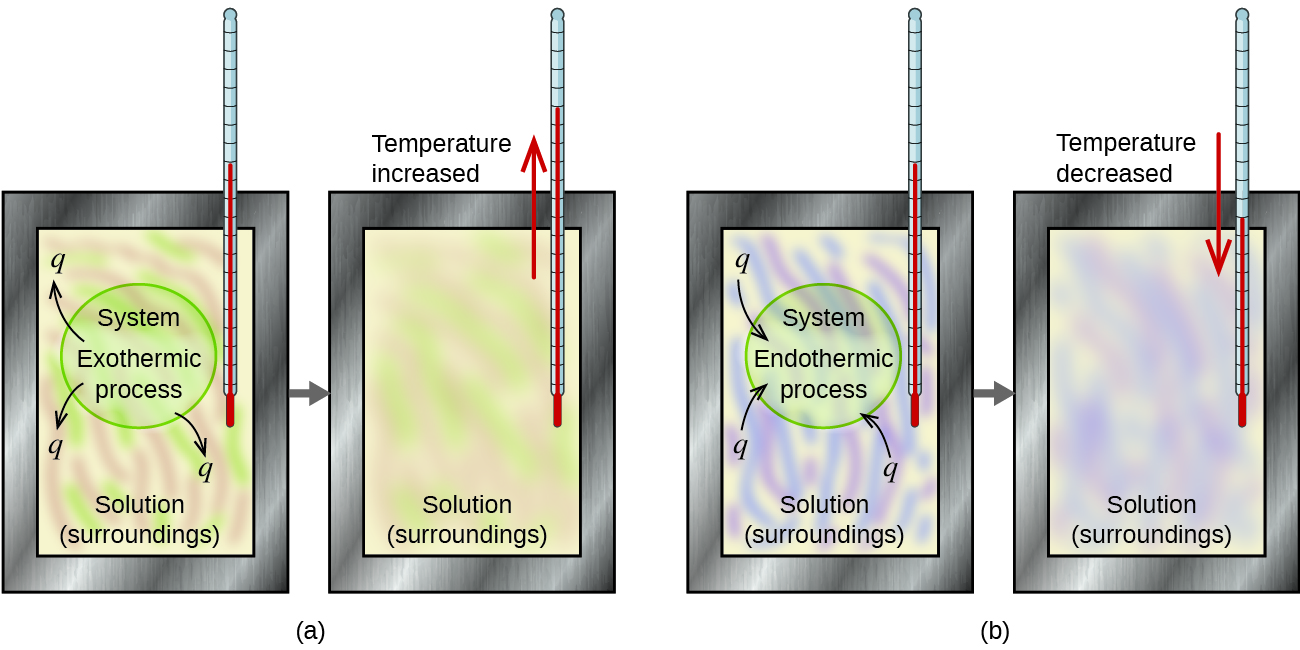
Figure 3.5.2. In a calorimetric determination, either (a) an exothermic process occurs and heat, q, is negative, indicating that thermal energy is transferred from the system to its surroundings, or (b) an endothermic process occurs and heat, q, is positive, indicating that thermal energy is transferred from the surroundings to the system.

Scientists use well-insulated calorimeters that all but prevent the transfer of heat between the calorimeter and its environment. This enables the accurate determination of the heat involved in chemical processes, the energy content of foods, and so on.

Consider a simple example that illustrates the core idea behind calorimetry. Suppose we initially have a high-temperature substance, such as a hot piece of metal (M), and a low-temperature substance, such as cool water (W). If we place the metal in the water, heat will flow from M to W. The temperature of M will decrease, and the temperature of W will increase until the two substances have the same temperature— when they reach thermal equilibrium (Figure 3.5.3). If this occurs in a calorimeter, ideally all of this heat transfer occurs between the two substances, with no heat gained or lost by either the calorimeter or the calorimeter’s surroundings. Under these ideal circumstances, the net heat change is zero:

q_{substance M}+ q_{substance W} = 0

This relationship can be rearranged to show that the heat lost by substance M is equal to the heat gained by substance W:

– q_{substance M} = q_{substance W}

Recall the first law of thermodynamics: energy is neither gained nor destroyed, only transferred. For calorimetry problems, keep in mind that heat flows in only one direction – always from hot to cold. So while one substance emits heat, the other substance will absorb that heat. The magnitude of the heat (change) is, therefore, the same for both substances, and the negative sign merely shows that q_{substance M} and q_{substance W} are opposite in direction of heat flow (gain or loss) but does not indicate the arithmetic sign of either q value (that is determined by whether the matter in question gains or loses heat, per definition). In the specific situation described, q_{substance M} is a negative value and q_{substance W} is positive, since heat is transferred from M to W.

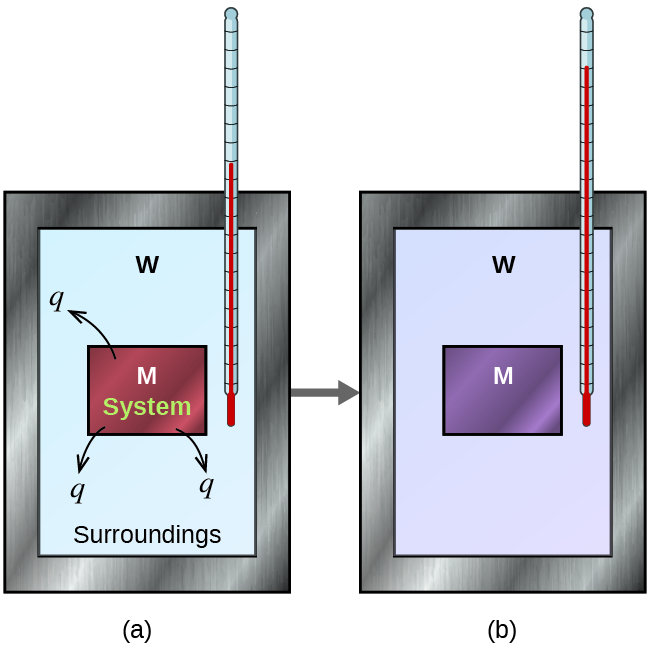
Figure 3.5.3. In a simple calorimetry process, (a) heat, q, is transferred from the hot metal, M, to the cool water, W, until (b) both are at the same temperature.

Here, we’ll talk about two types of calorimeters – “coffee-cup” calorimeters and bomb calorimeters.

“Coffee-Cup” (or Constant Pressure) Calorimetry

General chemistry students often use simple calorimeters constructed from polystyrene cups (Figure 3.5.4). These easy-to-use “coffee cup” calorimeters operate at constant pressure to allow more heat exchange with the outside environment and therefore produce less accurate energy values. In terms of real applications, these calorimeters are most appropriate for endothermic and mildly exothermic processes. Highly exothermic reactions, such as combustion reactions, are typically carried out using bomb calorimeters (which we discuss later).

Figure 3.5.4. A simple calorimeter can be constructed from two polystyrene cups. A thermometer and stirrer extend through the cover into the reaction mixture.

Commercial solution calorimeters are also available. Relatively inexpensive calorimeters often consist of two thin-walled cups that are nested in a way that minimizes thermal contact during use, along with an insulated cover, handheld stirrer, and simple thermometer. More expensive calorimeters used for industry and research typically have a well-insulated, fully enclosed reaction vessel, motorized stirring mechanism, and a more accurate temperature sensor (Figure 3.5.5).

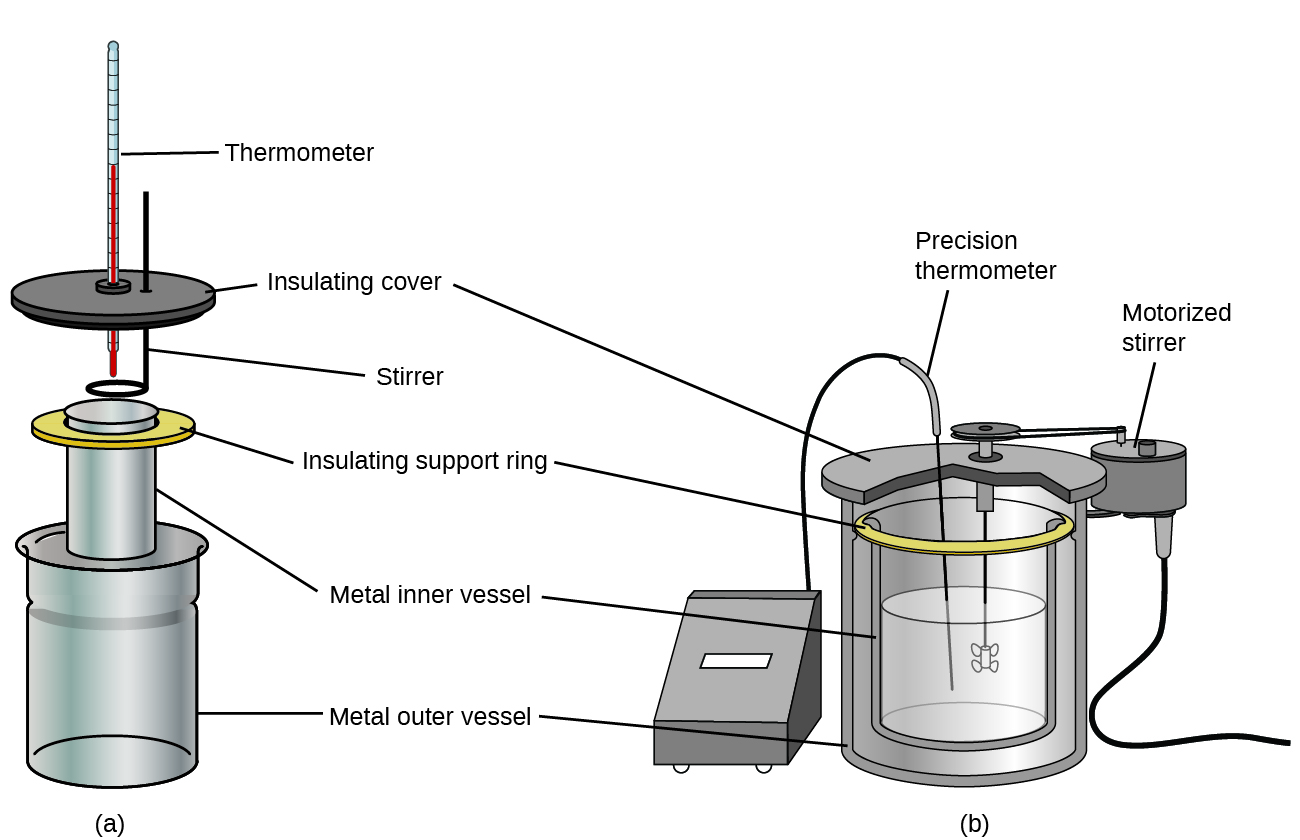
Figure 3.5.5. Commercial solution calorimeters range from (a) simple, inexpensive models for student use to (b) expensive, more accurate models for industry and research.

Example 3.5.3 – Heat Transfer between Substances at Different Temperatures

A 360.0-g piece of rebar (a steel rod used for reinforcing concrete) is dropped into 425 mL of water at 24.0°C. The final temperature of the water was measured as 42.7°C. Calculate the initial temperature of the piece of rebar. Assume the specific heat of steel is approximately the same as that for iron (see the Table 3.5.1) of specific heats for common substances), and that all heat transfer occurs between the rebar and the water (there is no heat exchange with the surroundings).

Solution

The temperature of the water increases from 24.0°C to 42.7°C, so the water absorbs heat. That heat came from the piece of rebar, which initially was at a higher temperature. Assuming that all heat transfer was between the rebar and the water, with no heat “lost” to the outside environment, then heat given off by rebar = −heat taken in by water, or:

q_rebar = – q_water

Since we know how heat is related to other measurable quantities, we

have:

(c × m × ΔT)_rebar = – (c × m × ΔT)_water

Letting f = final and i = initial, in expanded form, this becomes:

c_rebar × m_rebar × (T_f,rebar – T_i,rebar) = – c_water × m_water × (T_f,water -T_i,water)

The density of water is 1.0 g/mL, so 425 mL of water = 425 g. Noting that the final temperature of both the rebar and water is 42.7°C, substituting known values yields:

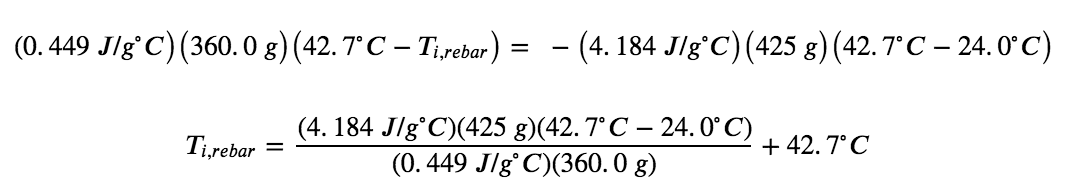
Solving this gives T_i,rebar= 248°C, so the initial temperature of the rebar was 248°C.

Check Your Learning 3.5.3 – Heat Transfer between Substances at Different

Temperatures

A 248-g piece of copper is dropped into 390 mL of water at 22.6°C. The final temperature of the water was measured as 39.9°C. Calculate the initial temperature of the piece of copper. Assume that all heat transfer occurs between the copper and the water.

Answer

The initial temperature of the copper was 335.6°C.

Check Your Learning 3.5.4 – Heat Transfer between Substances at Different

Temperatures

A 248-g piece of copper initially at 314°C is dropped into 390 mL of water initially at 22.6°C. Assuming that all heat transfer occurs between the copper and the water, calculate the final temperature.

Answer

The final temperature (reached by both copper and water) is 38.7°C.

This method can also be used to determine other quantities, such as the specific heat of an unknown metal.

Example 3.5.4 – Identifying a Metal by Measuring Specific Heat

A 59.7 g piece of metal that had been submerged in boiling water was quickly transferred into 60.0 mL of water initially at 22.0°C. The final temperature is 28.5°C. Use these data to determine the specific heat of the metal. Use this result to identify the metal.

Solution

Assuming perfect heat transfer, heat given off by metal = −heat taken in by water, or:

q_metal = – q_water

In expanded form, this is:

c_metal × m_metal × (T_f,metal – T_i,metal) = – c_water × m_water × (T_f,water – T_i,water)

Noting that since the metal was submerged in boiling water, its initial temperature was 100.0°C; and that for water, 60.0 mL = 60.0 g; we have:

(c_metal)(59.7 g)(28.5°C- 100°C) = – (4.18 J/g°C)(60.0 g)(28.5°C – 22.0°C)

C_metal= 0.38 J/g°C

Comparing this with values in the table (Table 3.5.1) of specific heats of common substances, our experimental specific heat is closest to the value for copper (0.39 J/g °C), so we identify the metal as likely copper.

Check Your Learning 3.5.5 – Identifying a Metal by Measuring Specific Heat

A 92.9-g piece of a silver/gray metal is heated to 178.0°C, and then quickly transferred into 75.0 mL of water initially at 24.0°C. After 5 minutes, both the metal and the water have reached the same temperature: 29.7°C. Determine the specific heat and the identity of the metal. (Note: You should find that the specific heat is close to that of two different metals. Explain how you can confidently determine the identity of the metal).

Answer

c_metal = 0.13 J/g °C

This specific heat is close to that of either gold or lead. It would be difficult to determine which metal this was based solely on the numerical values. However, the observation that the metal is silver/gray in addition to the value for the specific heat indicates that the metal is lead.

When we use calorimetry to determine the heat involved in a chemical reaction, the same principles we have been discussing apply. The amount of heat absorbed by the calorimeter is often small enough that we can neglect it (though not for highly accurate measurements, as discussed later), and the calorimeter minimizes energy exchange with the outside environment. Because energy is neither created nor destroyed during a chemical reaction, there is no overall energy change during the reaction. The heat produced or consumed in the reaction (the “system”), q_reaction, plus the heat absorbed or lost by the solution (the “surroundings”), q_solution, must add up to zero:

q_reaction + q_solution = 0

This means that the amount of heat produced or consumed in the reaction equals the amount of heat absorbed or lost by the solution:

q_reaction = – q_solution

This concept lies at the heart of all calorimetry problems and calculations. If the amount of heat absorbed by a calorimeter is too large to neglect or if we require more accurate results, then we must take into account the heat absorbed both by the solution and by the calorimeter.

Example 3.5.5 – Heat Produced by an Exothermic Reaction

When 50.0 mL of 1.00 M HCl (aq) and 50.0 mL of 1.00 M NaOH (aq), both at 22.0°C, are added to a coffee cup calorimeter, the temperature of the mixture reaches a maximum of 28.9°C. What is the approximate amount of heat produced by this reaction? You may assume that the volumes are additive.

HCl (aq) + NaOH (aq)  →  NaCl (aq) + H₂O (l)

Solution

To visualize what is going on, imagine that you could combine the two solutions so quickly that no reaction took place while they mixed; then after mixing, the reaction took place. At the instant of mixing, you have 100.0 mL of a mixture of HCl and NaOH at 22.0°C, and hence it will be that whole solution of 100.0 mL that will absorb the heat given off by the reaction. The HCl and NaOH then react until the solution temperature reaches 28.9°C.

The heat given off by the reaction is equal to that taken in by the solution.

Therefore:

q_reaction = – q_solution

(It is important to remember that this relationship only holds if the calorimeter does not absorb any heat from the reaction, and there is no heat exchange between the calorimeter and the outside environment.)

Next, we know that the heat absorbed by the solution depends on its specific heat, mass, and temperature change:

q_solution = (c × m × ΔT)_solution

To proceed with this calculation, we need to make a few more reasonable assumptions or approximations. Since the solution is aqueous, we can proceed as if it were water in terms of its specific heat and mass values. The density of water is approximately 1.0 g/mL, so 100.0 mL has a mass of about 1.0 × 10² g (two significant figures). The specific heat of water is approximately 4.184 J/g °C, so we use that for the specific heat of the solution. Substituting these values gives:

q_solution = (4.184 J/g°C)(1.0 × 10² g)(28.9°C – 22.0°C) = 2.9 × 10³ J

Finally, since we are trying to find the heat of the reaction, we have:

q_reaction = – q_solution = -2.9 × 10³ J

The negative sign indicates that the reaction is exothermic. It produces 2.9 kJ of heat.

Check Your Learning 3.5.6 – Heat Produced by an Exothermic Reaction

When 100 mL of 0.200 M NaCl (aq) and 100 mL of 0.200 M AgNO₃ (aq), both at 21.9°C, are mixed in a coffee cup calorimeter, the temperature increases to 23.5°C as solid AgCl forms. How much heat is produced by this precipitation reaction? What assumptions did you make to determine your value?

Answer

1.34 × 10³ J; assume the volumes are additive, no heat is absorbed by the calorimeter, no heat is exchanged between the calorimeter and its surroundings, and that the specific heat and mass of the solution are the same as those for water.

As seen in the previous example, we assumed that the specific heat capacity of the solution mixture of HCl (aq) and NaOH (aq) was equal to that for water. Therefore, in calorimetry problems (unless otherwise mentioned), you can set the value of c for solutions as 4.184 J/g °C if the assumption is reasonable (for example, the reactants used are all aqueous solutions).

Example 3.5.6 – Heat Flow in an Instant Ice Pack

When solid ammonium nitrate dissolves in water, the solution becomes cold. This is the basis for an “instant ice pack” (Figure 3.5.6). When 3.21 g of solid NH₄NO₃ dissolves in 50.0 g of water at 24.9°C in a calorimeter, the temperature decreases to 20.3°C.

Calculate the value of q for this reaction and explain the meaning of its arithmetic sign. State any assumptions that you made.

Figure 3.5.6. An instant cold pack consists of a bag containing solid ammonium nitrate and a second bag of water. When the bag of water is broken, the pack becomes cold because the dissolution of ammonium nitrate is an endothermic process that removes thermal energy from the water. The cold pack then removes thermal energy from your body.

Solution

We assume that the calorimeter prevents heat transfer between the solution and its external environment (including the calorimeter itself), in which case:

q_rxn = – q_soln

with “rxn” and “soln” used as shorthand for “reaction” and “solution,” respectively.

Note: We’re saying here that it’s the solution that is losing heat, and not the solvent. In your calculations, when you consider the value for mass, m, you have to use the mass of the solution, NOT the solvent! When the reaction begins, the amount of salt is already dissolved and added to the amount of water present, so the solution is present and will be the one that emits heat. By the law of conservation of mass, the total mass of the solution must be the sum of masses for salt and water, hence it is this total mass of solution that loses heat:

m_soln= m_water+ m_SaH = 50.0g +3.21g = 53.2g

Assuming also that the specific heat of the solution is the same as that for water, we have:

q_rxn = – q_soln = – (c × m × ΔT)_soln

= – [(4.184 J/g°C) × (53.2 g) × (20.3°C – 24.9°C)]

= – [(4.184 J/g°C) × (53.2 g) × (- 4.6°C)]

= + 1.0 × 10³ J = + 1.0kJ

The positive sign for q indicates that the dissolution is an endothermic process.

Check Your Learning 3.5.7 – Heat Flow in an Instant Ice Pack

When a 3.00-g sample of KCl was added to 3.00 × 10² g of water in a coffee cup calorimeter, the temperature decreased by 1.05°C. How much heat is involved in the dissolution of the KCl? What assumptions did you make?

Answer

1.33 kJ; assume that the calorimeter prevents heat transfer between the solution and its external environment (including the calorimeter itself) and that the specific heat of the solution is the same as that for water

Bomb (or Constant Volume) Calorimetry

The coffee-cup calorimeters previously described are designed to operate at constant (atmospheric) pressure and are convenient to measure heat flow accompanying processes that occur in solution. A different type of calorimeter that operates at constant volume, a bomb calorimeter, is used to measure the energy produced by reactions that are very exothermic and yield large amounts of heat and gaseous products, such as combustion reactions. This type of calorimeter consists of a robust steel container (the “bomb”) that contains the reactants and is itself submerged in water (Figure 3.5.8). The sample is placed in the bomb, which is then filled with oxygen at high pressure. A small electrical spark is used to ignite the sample. The energy produced by the reaction is absorbed by the steel bomb and the surrounding water. The temperature increase is measured and, along with the known heat capacity of the calorimeter, is used to calculate the energy produced by the reaction. Bomb calorimeters require calibration to determine the heat capacity of the calorimeter and ensure accurate results. The calibration is accomplished using a reaction with a known q, such as a measured quantity of benzoic acid ignited by a spark from a nickel fuse wire that is weighed before and after the reaction. The temperature change produced by the known reaction is used to determine the heat capacity of the calorimeter. The calibration is generally performed each time before the calorimeter is used to gather research data.

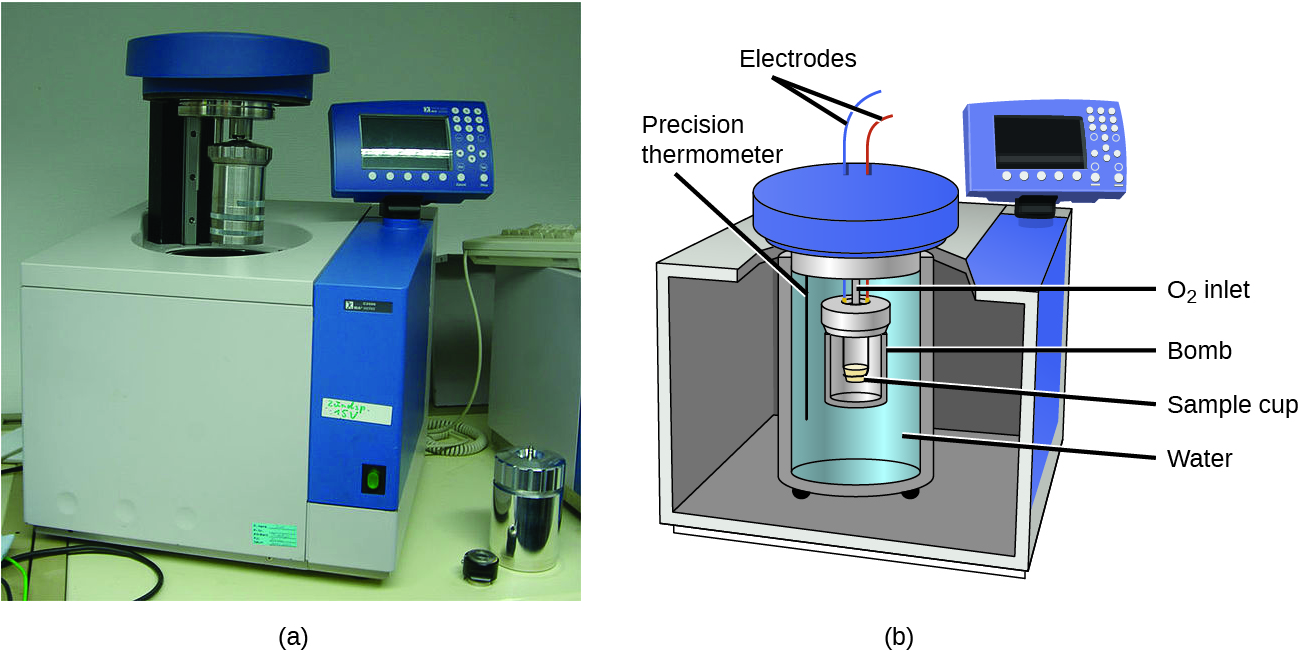
Figure 3.5.8. (a) A bomb calorimeter is used to measure the heat produced by reactions involving gaseous reactants or products, such as combustion. (b) The reactants are contained in the gas-tight “bomb,” which is submerged in water and surrounded by insulating materials. (credit a: modification of work by “Harbor1”/Wikimedia commons)

Example 3.5.7 – Bomb Calorimetry

When 3.12 g of glucose, C₆H₁₂O₆, is burned in a bomb calorimeter, the temperature of the calorimeter increases from 23.8°C to 35.6°C. The calorimeter contains 775 g of water, and the bomb itself has a heat capacity of 893 J/°C.

(a) How much heat was produced by the combustion of the glucose sample?

(b) The metabolic breakdown of glucose is quite similar to its combustion – it requires oxygen (O₂) for its oxidation, except the energy harvested from glucose is primarily used to carry out cellular processes. Assuming the same amount of energy from part (a) was harnessed from consuming the same glucose sample and metabolizing it, how much nutritional calories (Cal) would this correspond to?

Solution

(a) The combustion produces heat that is primarily absorbed by the water and the bomb. (The amounts of heat absorbed by the reaction products and the unreacted excess oxygen are relatively small and dealing with them is beyond the scope of this text. We will neglect them in our calculations.)

The heat produced by the reaction is absorbed by the water and the bomb:

q_rxn = – (q_water + q_bomb) = – {[m_water × c_water × (T_f – T_i)] + [C_cal × (T_f -T_i)]}

= – [(4,184 J/g°C) × (775 g) × (35.6°C- 23.8°C) + 893 J/°C × (35.6°C – 23.8°C)]

= – (38300 J + 10500 J)

= – 48800 J = – 48.8 kJ

This reaction released 48.7 kJ of heat when 3.12 g of glucose was burned.

(b) The energy produced, expressed in kilojoules, can easily be expressed in calories and furthermore in Calories by performing a unit conversion:

Therefore, a person consuming 3.12 g of glucose would get roughly 11.6 Calories.

Check Your Learning 3.5.8 – Bomb Calorimetry

When 0.963 g of benzene, C₆H₆, is burned in a bomb calorimeter, the temperature of the calorimeter increases by 8.39°C. The bomb has a heat capacity of 784 J/°C and is submerged in 925 mL of water. How much heat was produced by the combustion of the glucose sample?

Answer

39.0 kJ

Questions

★ Questions

1. A 500-mL bottle of water at room temperature and a 2-L bottle of water at the same temperature were placed in a refrigerator. After 30 minutes, the 500-mL bottle of water had cooled to the temperature of the refrigerator. An hour later, the 2-L of water had cooled to the same temperature. When asked which sample of water lost the most heat, four students gave the following answers,

         a. Both bottles lost the same amount of heat because they started at the                     same temperature and finished at the same temperature.

         b. The 2-L bottle of water lost more heat because there was more water.

         c. The 500-mL bottle of water lost more heat because it cooled more quickly.

         d. It’s not possible to tell because we do not know the initial temperature and             the final temperature of the water.

Indicate which of these answers is correct and describe the error in each of the other answers.

  2. Would the amount of heat measured in an exothermic reaction be greater,             lesser, or remain the same if we used a calorimeter that was a poorer insulator           than a coffee cup calorimeter? Explain your answer.

  3. Would the amount of heat absorbed by the dissolution in Example 6. (heat flow    in an instant ice pack) appear greater, lesser, or remain the same if the                          experimenter used a calorimeter that was a poorer insulator than a coffee cup            calorimeter? Explain your answer.

★★ Questions

  4. How many millilitres of water (volume) at 23 °C with a density of 1.00 g/mL           must be mixed with 180 mL (about 6 oz) of coffee at 95 °C so that the resulting       combination will have a temperature of 60 °C? Assume that coffee and water           have the same density and the same specific heat.

  5. How much will the temperature of a cup (180 g) of coffee at 95 °C be reduced       when a 45 g silver spoon (specific heat 0.24 J/g °C) at 25 °C is placed in the coffee     and the two are allowed to reach the same temperature? Assume that the coffee     has the same density and specific heat as water.

  6. When 50.0 g of 0.200 M NaCl(aq) at 24.1 °C is added to 100.0 g of 0.100 M             AgNO₃(aq) at 24.1 °C in a calorimeter, the temperature increases to 25.2 °C as             AgCl(s) forms. Assuming the specific heat of the solution and products is 4.20 J/g       °C, calculate the approximate amount of heat in joules produced.

  7. The addition of 3.15 g of Ba(OH)₂·8H₂O to a solution of 1.52 g of NH₄SCN in 100      g of water in a calorimeter caused the temperature to fall by 3.1 °C. Assuming the      specific heat of the solution and products is 4.20 J/g °C, calculate the approximate    amount of heat absorbed by the reaction (in kilojoules), which can be represented    by the following equation:

Ba(OH)₂ ・ 8H₂O (s) + 2 NH₄SCN (aq)  →  Ba(SCN)₂ (aq) + 2 NH₃ (aq) + 10 H₂O (l)

  8. When 1.0 g of fructose, C₆H₁₂O₆(s), a sugar commonly found in fruits, is burned    in oxygen in a bomb calorimeter, the temperature of the calorimeter increases by      1.58 °C. If the heat capacity of the calorimeter and its contents is 9.90 kJ/°C, what       is q for this combustion (in kilojoules)?

  9. When a 0.740-g sample of trinitrotoluene (TNT), C₇H₅N₂O₆, is burned in a             bomb calorimeter, the temperature increases from 23.4 °C to 26.9 °C. The heat           capacity of the calorimeter is 534 J/°C, and it contains 675 mL of water. How much   heat was produced by the combustion of the TNT sample (in kilojoules)?

  10. The amount of fat recommended for someone with a daily diet of 2000                Calories is 65 g. What percent of the calories in this diet would be supplied by this    amount of fat if the average number of Calories for fat is 9.1 Calories/g?

  11. A teaspoon of the carbohydrate sucrose (common sugar) contains 16 Calories        (16 kcal). What is the mass of one teaspoon of sucrose (in grams) if the average        number of Calories for carbohydrates is 4.1 Calories/g?

  12. A pint of premium ice cream can contain 1100 Calories. What mass of fat, in         grams and pounds, must be produced in the body to store an extra 1.1 × 10³                 Calories if the average number of Calories for fat is 9.1 Calories/g?

  13. Which is the least expensive source of energy in kilojoules per dollar: a box of      breakfast cereal that weighs 32 ounces and costs $4.23, or a litre of isooctane           (density, 0.6919 g/mL) that costs $0.45? Compare the nutritional value of the cereal   with the heat produced by combustion of the isooctane under standard                       conditions. A 1.0-ounce serving of the cereal provides 130 Calories.

Answers

1. Student 2 is correct. The error in the first student’s answer is having ignored the mass of water. For the third student, the answer opposed the question asked. He needed to state that the 2-L bottle took longer to reach the refrigerator’s temperature therefore it lost more heat. The error in the fourth student’s answer ignored that the change in temperature of both water bottles are the same and both initial and final temperature are not needed.

  2. Lesser; in a poorer insulator more of the heat produced by the reaction will            escape, which would appear as a smaller value for q.

  3. Greater, since taking the calorimeter’s heat capacity into account will                       compensate for the thermal energy transferred to the solution from the                       calorimeter; this approach includes the calorimeter itself, along with the solution,     as “surroundings”: q_rxn = − (q_solution + q_calorimeter); since both q_solution and         q_calorimeter are negative, including the latter term (q_rxn) will yield a greater value   for the heat of the dissolution

  4. 170.27 mL

  5. The temperature of the coffee will drop 1 degree.

  6. 693 J

  7. 1.4 kJ

  8. 15.64 kJ

  9. 11.7 kJ

  10. 30%

  11. 3.90 g

  12. 120.87 g, 0.055 lbs

  13. Buying a dollar of isooctane it would give you 7.349 x 10⁴ kJ. A dollar worth of      cereal would only fuel 4.12 kJ of energy. Therefore, with one dollar it is best to            invest in isooctane to obtain more energy.