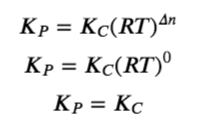4.2 – The Equilibrium Constant & Reaction Quotient

In the last section, we began deriving a constant for chemical equilibria based on the kinetics of the forward and reverse reactions. We established that the composition of the equilibrium mixture is determined by the magnitudes of the rate constants for the forward and the reverse reactions, or more specifically, that the equilibrium constant is equal to the rate constant for the forward reaction divided by the rate constant for the reverse reaction. Here, we’ll develop an equilibrium constant expression for K applicable to any equilibrium reaction and look at how we can also predict the direction of net change given a set amount of reactants & products.

The Equilibrium Constant (K)

In 1864, the Norwegian chemists Cato Guldberg (1836–1902) and Peter Waage (1833–1900) carefully measured the compositions of many reaction systems at equilibrium. They discovered that for any reversible reaction of the general form

m A + n B   ⇌   x C + y D

where A and B are reactants, C and D are products, and m, n, x, and y are the stoichiometric coefficients in the balanced chemical equation for the reaction, the ratio of the product of the equilibrium quantities of the products (raised to their coefficients in the balanced chemical equation) to the product of the equilibrium concentrations of the reactants (raised to their coefficients in the balanced chemical equation) is always a constant under a given set of conditions. This relationship was eventually summarized as follows: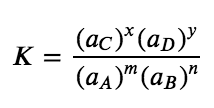

Equation 4.2.1 Equilibrium Constant

where K is the equilibrium constant for the reaction, equivalent to the value defined in Section 4.1, and a_X represents the activity of each species participating in the equilibrium. The chemical equilibrium equation represented with reactants A & B and products C & D is called the equilibrium equation, and the right side of the mathematical equation above is called the equilibrium constant expression. The relationship shown in the expression for K is true for any pair of opposing reactions regardless of the mechanism of the reaction or the number of steps in the mechanism.

An important fact to note is that equilibrium constants are dimensionless (they have no units) but the temperature at which this value is valid must always be listed (since K is temperature dependent). This is due to computing K values using the activities of the reactants and products in the equilibrium system. The activity of a substance is a measure of its effective concentration under specified conditions. While a detailed discussion of this important quantity is beyond the scope of an introductory text, it is necessary to be aware of a few important aspects:

• Activities are dimensionless (unitless) quantities and are in essence “adjusted” quantities of reactants and products.
• For relatively dilute solutions, a solute’s activity and its molar concentration are roughly equal (i.e. for a solute X, a_X ≈ [X] in mol/L or M). Note that this approximation does not hold for highly concentrated solutes.
• For gases, a substance’s activity is equal to its partial pressure (i.e. a_X = P_X in bar)
• Activities for pure condensed phases (solids and liquids) are equal to 1 (i.e. a_X = 1), hence their activities do not appear in the expression for K

Further discussion about activities can be found here.

We categorize equilibria into two types: homogeneous and heterogeneous. A homogeneous equilibrium is one in which all of the reactants and products are present in a single solution (by definition, a homogeneous mixture). In this chapter, we will concentrate on the two most common types of homogeneous equilibria: those occurring in liquid-phase solutions and those involving exclusively gaseous species. A heterogeneous equilibrium is a system in which reactants and products are found in two or more phases. The phases may be any combination of solid, liquid, or gas phases, and solutions. When dealing with these equilibria, remember that solids and pure liquids do not appear in equilibrium constant expressions (as we’ve mentioned above, the activities of pure solids, pure liquids, and solvents are 1).

Example 4.2.1 – Writing Equilibrium Constant Expressions

Write the equilibrium constant expression for each reaction.

(a) N₂ (g) + 3 H₂ (g)  ⇌  2 NH₃ (g)

(b) 2 CO₂ (g)  ⇌  2 CO (g) + O₂ (g)

(c) H₂O (l) + H₂CO₃ (aq)  ⇌  H₃O⁺ (aq) + HCO₃^– (aq)

(d) Fe₃O₄ (s) + 4 H₂ (g)  ⇌  3 Fe (s) + 4 H₂O (g)  

(e) Cu(s) +  Zn²⁺(aq)  ⇌  Cu²⁺(aq) + Zn(s) 

Solution

(a) The only product is ammonia, which has a coefficient of 2. For the reactants, N₂ has a coefficient of 1 and H₂ has a coefficient of 3. All species are gases, and so their activities are equal to their partial pressures. The equilibrium constant expression is as follows:  

(b) The products are CO, with a coefficient of 2, and O₂, with a coefficient of 1. The only reactant is carbon dioxide, which has a coefficient of 2. Since all species are gases, the equilibrium constant expression is as follows:  

(c) This reaction contains a pure liquid (H2O), its activity is equal to 1 and thus does not appear in the equilibrium constant expression. The other three species are solutes, and their activities can be approximated using their molar concentrations:   

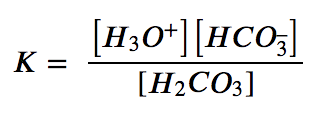
(d) This reaction contains two pure solids (Fe3O4 and Fe), which do not appear in the equilibrium constant expression (their activities are equal to 1). However, the two gases do appear in the expression, as partial pressures: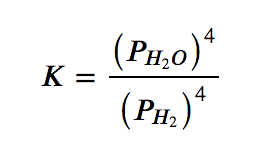 

(e) This reaction contains two pure solids (Cu and Zn), which do not appear in the equilibrium constant expression (their activities are equal to 1). However, the two aqueous ions do appear in the expression, as molar concentrations: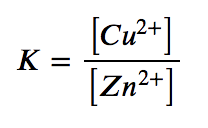 

Check Your Learning 4.2.1 – Writing Equilibrium Constant Expressions

Write the equilibrium constant expression for each reaction.

(a) N₂O (g) ⇌ N₂ (g) + 1/2 O₂ (g)

(b) H₂O (l) + HOCl (aq) ⇌ H₃O⁺(aq) + OCl^– (aq)

(c) H₂ (g) + I₂ (g) ⇌ 2 HI (g)

(d) CaCO₃ (s) ⇌ CaO (s) + CO₂ (g)

(e) BaSO₄(s) ⇌ Ba²⁺(aq) + SO₄^2–(aq) 

Answer:

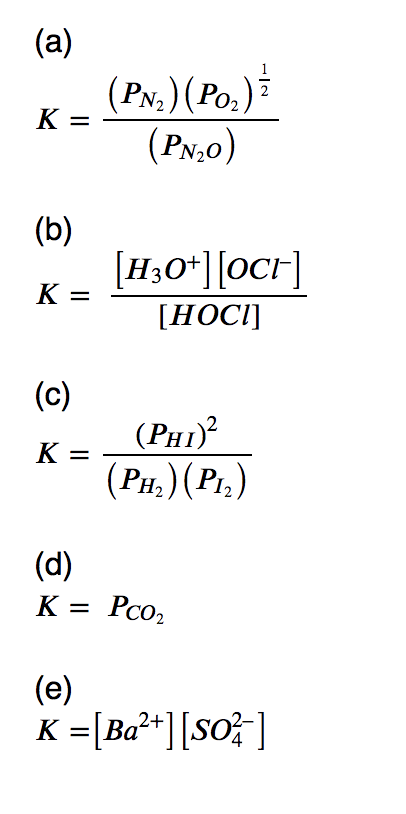
Manipulating Equilibrium Constants

Reversing the Equilibrium Equation

Because equilibrium can be approached from either direction in a chemical reaction, the equilibrium constant expression and thus the magnitude of the equilibrium constant depend on the form in which the chemical reaction is written. For example, if we write the generic equilibrium reaction equation in reverse, we obtain the following:

x C  +  y D   ⇌   m A  +  n B

If all species are solutes, then the corresponding equilibrium constant K’ is as follows:

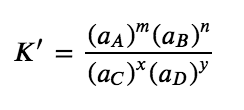
Equation 4.2.2 Reverse Equilibrium Constant

This expression is the inverse of the expression for the original equilibrium constant, so K’ = 1/K. That is, when we write a reaction in the reverse direction, the equilibrium constant expression is inverted. Below is an example:

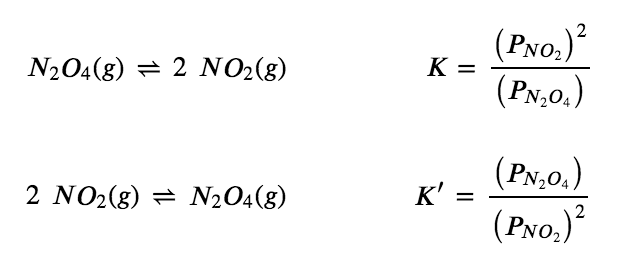
Consider another example, the formation of water: 2 H₂ (g) + O₂ (g) ⇌ 2 H₂O (g). Because H₂ is a good reductant and O₂ is a good oxidant, this reaction has a very large equilibrium constant (K = 2.4 × 10⁴⁷ at 500 K). Consequently, the equilibrium constant for the reverse reaction, the decomposition of water to form O₂ and H₂, is very small: K ^‘ = 1/K = 1/(2.4 × 10⁴⁷) = 4.2 × 10⁻⁴⁸. As suggested by the very small equilibrium constant, the dynamic equilibrium always very heavily favours the formation of water molecules. This is related to the fact that the decomposition of water into O₂ and H₂ requires a substantial amount of activation energy; a concept we will return to in our study of Chemical Kinetics (Chapter 7).

Altering Species Coefficients

Writing an equation in different but chemically equivalent forms also causes both the equilibrium constant expression and the magnitude of the equilibrium constant to be different. For example, going back to our inverse equilibrium equation with an equilibrium constant K ^‘, we could write the equation for that reaction

2 NO₂ (g)  ⇌  N₂O₄ (g)

as

 NO₂ (g)  ⇌  ½ N₂O₄ (g)

with the equilibrium constant K”  as follows:

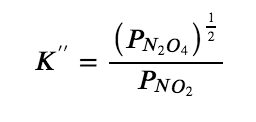
The values for K′ and K″ are related as follows:

 Equation 4.2.3 K’ and K” relation

In general, if all the coefficients in a balanced chemical equation were subsequently multiplied by n, then the new equilibrium constant is the original equilibrium constant raised to the n^th power.

Combining Chemical Equilibrium Equations

Chemists frequently need to know the equilibrium constant for a reaction that has not been previously studied. In such cases, the desired reaction can often be written as the sum of other reactions for which the equilibrium constants are known. The equilibrium constant for the unknown reaction can then be calculated from the tabulated values for the other reactions.

To illustrate this procedure, let’s consider the reaction of N₂ with O₂ to give NO₂. This reaction is an important source of the NO₂ that gives urban smog its typical brown color. The reaction normally occurs in two distinct steps. In the first reaction (1), N₂ reacts with O₂ at the high temperatures inside an internal combustion engine to give NO. The released NO then reacts with additional O₂ to give NO₂ (2). The equilibrium constant for each reaction at 100°C is also given.

(1) N₂ (g) + O₂ (g)  ⇌  2 NO (g)               K₁ = 2.0 x 10^–25

(2) 2 NO (g) + O₂ (g)  ⇌  2 NO₂ (g)         K₂ = 6.4 x 10⁹

Addition of reactions (1) and (2) gives the overall reaction of N₂ with O₂:

     (3)= (1) + (2)         N₂ (g) + 2 O₂ (g)  ⇌  2 NO₂ (g)          K₃ = ?

The equilibrium constant expressions for the reactions are as follows:

What is the relationship between K₁, K₂, and K₃, all at 100°C? The expression for K₁ has (P_NO2)²  in the numerator, the expression for K₂ has (P_NO2)²  in the denominator, and (P_NO2)²  does not appear in the expression for K₃. Multiplying K₁ by K₂ and canceling the (P_NO2)²  terms,

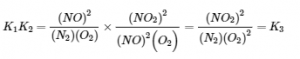
Thus the product of the equilibrium constant expressions for K₁ and K₂ is the same as the equilibrium constant expression for K₃:

The equilibrium constant for a reaction that is the sum of two or more reactions is equal to the product of the equilibrium constants for the individual reactions. In contrast, recall that according to Hess’s Law (seen in the previous chapter on thermochemistry), ΔH for the sum of two or more reactions is the sum of the ΔH values for the individual reactions.

Summary

It is important to remember that an equilibrium constant is always tied to a specific chemical equation, and if you manipulate the equation in any way, the value of K will change. Fortunately, the rules are very simple:

• Writing the equation in reverse will invert the equilibrium expression (i.e. K’ = 1/K)
• Multiplying the coefficients by a common factor n will raise K to the corresponding power of n (i.e. K’ = Kⁿ where n is a common factor)
• The equilibrium constant for a reaction that is the sum of several chemical equilibrium equations is the product of the equilibrium constants for each of the steps (i.e. K’ = K₁K₂K₃…)

Example 4.2.2 – Manipulating Equilibrium Constants – 1

At 745 K, K is 0.118 for the following reaction:

N₂ (g) + 3 H₂ (g)  ⇌  2 NH₃ (g)

What is the equilibrium constant for each related reaction at 745 K?

(a) 2 NH₃ (g)  ⇌  N₂ (g)  + 3 H₂ (g)

(b) 1/2 N₂ (g) + 3/2 H₂ (g)   ⇌   NH₃ (g)

Solution

The equilibrium constant expression for the given reaction of N₂ (g) with H₂ (g) to produce NH₃ (g) at 745 K is as follows:

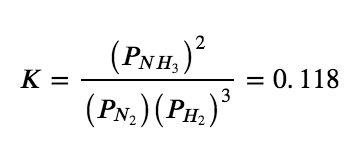
(a) This reaction is the reverse of the one given, so its equilibrium constant expression is as follows:

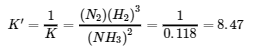
(b) In this reaction, the stoichiometric coefficients of the given reaction are divided by 2, so the equilibrium constant is calculated as follows:

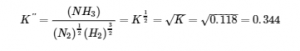
Check Your Learning 4.2.2 – Manipulating Equilibrium Constants – 1

At 527°C, the equilibrium constant for the reaction below is 7.9 × 10⁴.

2 SO₂ (g) + O₂ (g)  ⇌  2 SO₃ (g)

Calculate the equilibrium constant for the following reaction at the same

temperature:

SO₃ (g)  ⇌   SO₂ (g) +  ½ O₂ (g)

Answer:

3.6 × 10^-3

Example 4.2.3 – Manipulating Equilibrium Constants – 2

The following reactions occur at 1200°C:

(1) CO (g) + 3 H₂ (g)  ⇌  CH₄ (g) + H₂O (g)     K₁ = 9.17 × 10⁻²

(2) CH₄ (g) + 2 H₂S (g)  ⇌  CS₂ (g) + 4 H₂ (g)     K₂ = 3.3 × 10⁴

Calculate the equilibrium constant for the following reaction at the same temperature.

(3) CO (g) + 2 H₂S (g) ⇌ CS₂ (g) + H₂O (g) + H₂ (g)     K₃ = ?

Solution

The key to solving this problem is to recognize that reaction 3 is the sum of reactions 1 and 2:

(1) CO (g) + 3 H₂ (g)  ⇌  CH₄ (g) + H₂O (g)

(2) CH₄ (g) + 2 H₂S (g)  ⇌  CS₂ (g) + 4 H₂ (g)

(3)= (2) + (1)      CO (g) + 2 H₂S (g) ⇌ CS₂ (g) + H₂O (g) + H₂ (g)

The values for K₁ and K₂ are given, so it is straightforward to calculate K₃:

K₃ = K₁K₂ = (9.17 × 10^-2)(3.3 × 10⁴) = 3.03 × 10³

Check Your Learning 4.2.3 – Manipulating Equilibrium Constants – 2

In the first of two steps in the industrial synthesis of sulfuric acid, elemental sulfur reacts with oxygen to produce sulfur dioxide. In the second step, sulfur dioxide reacts with additional oxygen to form sulfur trioxide. The reaction for each step is shown, as is the value of the corresponding equilibrium constant at 25°C. Calculate the equilibrium constant for the overall reaction at this same temperature.

Answer

K₃ = 1.1 × 10⁶⁶

Equilibria Involving Gases

For reactions that involve species in solution, the concentrations used in equilibrium calculations are molarities, expressed in moles/litre. For gases, however, the activities of each reaction component are expressed in terms of partial pressures rather than molarity, where the standard state is 1 atm of pressure. Occasionally, the symbol K_P is used to highlight equilibrium constants calculated from partial pressures. For the general reaction mA + nB ⇌ xC + yD, in which all the components are gases, the equilibrium constant expression must be written as the ratio of the partial pressures of the products and reactants (each raised to its coefficient in the chemical equation):

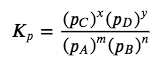
                            Equation 4.2.4 Gas Equilibrium Constant

Thus K_P for the decomposition of N₂O₄ is as follows:

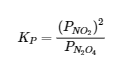
K_P is a unitless quantity because the quantity that is actually used to calculate it is an “effective pressure,” the ratio of the measured pressure to a standard state of 1 bar, which produces a unitless quantity. But what if we need to describe a gas-phase equilibrium in concentration units?

Because partial pressures are usually expressed in bars, the molar concentration of a gas and its partial pressure do not have the same numerical value. Consequently, if we were to recalculate K using molar concentrations (like solutes) instead of partial pressures, we would obtain a new equilibrium constant, known as K_C. The resulting numerical value of  K_C would very likely differ from K_P. They are, however, related by the ideal gas constant (R) and the absolute temperature (T) – this is because the partial pressure of a gas is directly proportional to its concentration at constant temperature. This relationship can be derived from the ideal gas equation, where M is the molar concentration of gas, n/V.

PV = nRT

P = (n/V)RT

P = MRT

Equation 4.2.5 Gas Pressure Proportionality

Thus, at constant temperature, the pressure of a gas is directly proportional to its concentration.

Hence, the equation relating K_C and K_P is derived as follows. For the gas-phase reaction mA + nB ⇌ xC + yD:

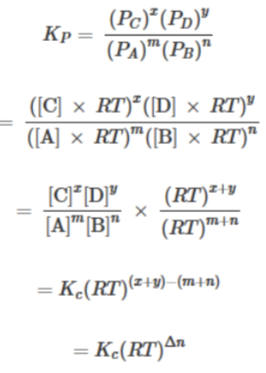
Therefore, relationship between K_C and K_P is

Equation 4.2.6 K_C and K_P Relation

where K_C is the equilibrium constant expressed in units of concentration (mol/L), K_P is the equilibrium constant expressed in units of pressure (bars), the temperature is expressed as the absolute temperature in Kelvin, R is the ideal gas constant in the appropriate units (R = 0.083145 bar•L/(mol•K)) and Δn is the difference between the sum of the coefficients of the gaseous products and the sum of the coefficients of the gaseous reactants in the reaction (the change in moles of gas between the reactants and the products). For the gas-phase reaction mA + nB ⇌ xC + yD, we have

Δn = (x + y) – (m + n)

Equation 4.2.7 Change in Moles of a Reaction

According to the equation above, K_P = K_C only if the moles of gaseous products and gaseous reactants are the same (i.e., Δn = 0).

For the decomposition of N₂O₄, there are 2 mol of gaseous product and 1 mol of gaseous reactant, so Δn = 1. Thus, for this reaction,

Example 4.2.4 – Calculation of K_P

Write the equations for the conversion of K_C to K_P for each of the following reactions:

(a) C₂H₆ (g)   ⇌   C₂H₄ (g)  +  H₂ (g)

(b) CO (g)  +  H₂O (g)   ⇌   CO₂ (g)  +  H₂ (g)

(c) N₂ (g)  +  3 H₂ (g)   ⇌   2 NH₃ (g)

Solution

(a) Δn = (2) − (1) = 1

K_P = K_C(RT)^Δn = K_C(RT)¹ = K_C(RT)

(b) Δn = (2) − (2) = 0

K_P = K_C(RT)^Δn = K_C(RT)⁰ = K_C

(c) Δn = (2) − (1 + 3) = −2

K_P = K_C(RT)^Δn = K_C(RT)⁻² =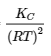

Check Your Learning 4.2.4 – Calculation of K_P

Write the equations for the conversion of K_C to K_P for each of the following reactions, which occur in the gas phase:

(a) 2 SO₂ (g) + O₂ (g)   ⇌   2 SO₃ (g)

(b) N₂O₄ (g)   ⇌   2 NO₂ (g)

(c) C₃H₈ (g) + 5 O₂ (g)   ⇌   3 CO₂ (g) + 4 H₂O (g)

Answer

(a) K_P = K_C(RT)⁻¹; (b) K_P = K_C(RT); (c) K_P = K_C(RT)

Example 4.2.5 – Calculation of K_P

Write the equation for the conversion of K_C to K_P for the following reaction, which occurs in the gas phase:

CS₂ (g)  + 4 H₂ (g)   ⇌   CH₄ (g)  +  2 H₂S (g)

K_C is equal to 0.28 for the following reaction at 900°C, what is K_P at this temperature?

Solution:

K_P = K_C(RT)^Δn = (0.28)[(0.0821)(1173)]⁻² = 3.0 × 10⁻⁵

Check Your Learning 4.2.5 – Calculation of K_P

Write the equation for the conversion of K_C to K_P for the following reaction, which occurs in the gas phase:

CH₃OH (g)  ⇌   CO (g) + 2 H₂ (g)

At 227°C, the following reaction has K_C = 0.0952, What would be the value of K_P at this temperature?

Answer:

160 or 1.6 × 10²

Example 4.2.6 – Calculation of K_P – The Haber Process

The equilibrium constant for the reaction of nitrogen and hydrogen to give ammonia is 0.118 at 745 K. The balanced equilibrium equation is as follows:

N₂ (g) + 3 H₂ (g) ⇌ 2 NH₃ (g)

What is K_P for this reaction at the same temperature?

Solution:

This reaction has 2 mol of gaseous product and 4 mol of gaseous reactants, so Δn = (2 − 4) = −2. We know K, and T = 745 K. Thus, we have the following:

Because K_P is a unitless quantity, the answer is K_P = 3.16 × 10⁻⁵.

Check Your Learning 4.2.6 – Calculation of K_P – The Haber Process

Calculate K_P for the reaction

2 SO₂ (g) + O₂ (g) ⇌ 2 SO₃ (g)

at 527°C, if K = 7.9 × 10⁴ at this temperature.

Answer:

K_P = 1.2 × 10³

The Reaction Quotient, Q

We previously saw that knowing the magnitude of the equilibrium constant under a given set of conditions allows chemists to predict the extent of a reaction. Often, however, chemists must decide whether a system has reached equilibrium or if the composition of the mixture will continue to change with time.

To determine whether a system has reached equilibrium, chemists use a quantity called the reaction quotient (Q). The expression for the reaction quotient has precisely the same form as the equilibrium constant expression, except that Q may be derived from a set of values measured at any time during the reaction of any mixture of the reactants and  products, regardless of whether the system is at equilibrium. Therefore, for the following general reaction:

m A  +  n B    ⇌    x C  + y D

the reaction quotient is defined as follows:

Equation 4.2.7 Reaction Quotient

Similarly to the equilibrium constant, the reaction quotient is dimensionless (no units) – this stems from using the species activities as its effective concentrations. As before, the activity of each species participating in the equilibrium can be represented as follows:

• For a solute X, a_X ≈ [X] in mol/L (note that again, this does not apply to highly concentrated solutions)
• For gases, a_X = P_X in bar
• For pure solids and liquids, a_X = 1

Example 4.2.6 – Writing Reaction Quotient Expressions

Write the expression for the reaction quotient (Qp and/or Qc) for each of the following reactions:

(a) 3 O₂ (g)   ⇌   2 O₃ (g)

(b) N₂ (g) + 3 H₂ (g)   ⇌   2 NH₃ (g)

(c) HCl (g) + NaOH (aq)   ⇌   NaCl (aq) + H₂O (l)

Solution

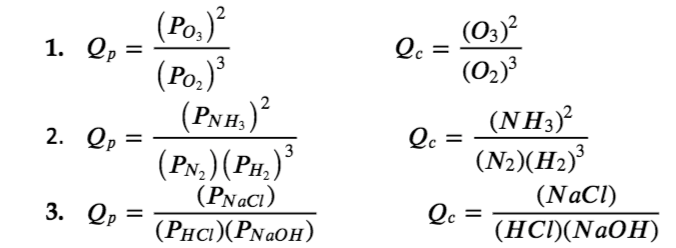
Check Your Learning 4.2.7 – Writing Reaction Quotient Expressions

Write the expression for the reaction quotient for each of the following reactions:

(a) 2 SO₂ (g) + O₂ (g)   ⇌   2 SO₃ (g)

(b) C₄H₈ (g)   ⇌   2 C₂H₄ (g)

(c) Cd²⁺ (aq) + 4 Cl^– (aq)   ⇌   CdCl₄^2- (aq)

Answer

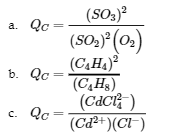
Example 4.2.8 – Evaluating a Reaction Quotient

Gaseous nitrogen dioxide forms dinitrogen tetroxide according to this equation:

2 NO₂ (g)  ⇌  N₂O₄ (g)

When 0.10 mol NO₂ is added to a 1.0-L flask at 25°C, the concentration changes so that at equilibrium, [NO₂]_eq = 0.016 mol/L and [N₂O₄]_eq = 0.042 mol/L.

(a) What is the value of the reaction quotient in concentration units, Q_C, before any reaction occurs?

(b) What is the value of the equilibrium constant in concentration units, K_C, for the reaction?

Solution

(a) Before any product is formed, [NO₂]_i = 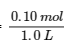= 0.10 mol/L, and [N₂O₄]_i = 0 mol/L. Thus,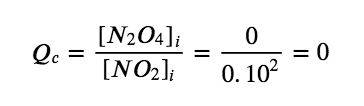 

(b) At equilibrium, the value of the equilibrium constant is equal to the value of the reaction quotient. At equilibrium,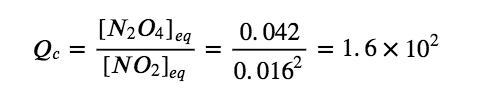

The equilibrium constant is 1.6 × 10².

Note that dimensional analysis would suggest the unit for this K_C value should be (mol/L)⁻¹. However, as mentioned previously, it is common practice to omit units for K_C values, since it is the magnitude of an equilibrium constant that relays useful information.

Check Your Learning 4.2.8 – Evaluating a Reaction Quotient

For the reaction 2 SO₂ (g) + O₂ (g)  ⇌ 2 SO₃ (g), the concentrations at equilibrium are [SO₂] = 0.90 mol/L, [O₂] = 0.35 mol/L, and [SO₃] = 1.1 mol/L. What is the value of the equilibrium constant, K_C?

Answer

K_C = 4.3

Predicting the Direction of Net Change Using Q

To understand how information is obtained using a reaction quotient, consider once again the dissociation of dinitrogen tetroxide to nitrogen dioxide,

N₂O₄ (g)   ⇌  2 NO₂ (g)

for which K = 4.65 × 10⁻³ at 298 K. We can write Q_C for this reaction as follows: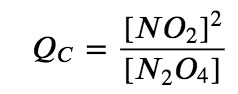The following table lists data from three experiments in which samples of the reaction mixture were obtained and analyzed at equivalent time intervals, and the corresponding values of Q were calculated for each. Each experiment begins with different proportions of product and reactant:

Experiment	[NO2] (mol/L)	[N2O4] (mol/L)
1	0	0.0400
2	0.0600	0
3	0.0200	0.0600

As these calculations demonstrate, Q can have any numerical value between 0 and infinity (undefined); that is, Q can be greater than, less than, or equal to K. Comparing the magnitudes of Q and K enables us to determine whether a reaction mixture is already at equilibrium and, if it is not, predict how its composition will change with time to reach equilibrium (i.e., whether the reaction will proceed to the right or to the left as written). All you need to remember is that the composition of a system not at equilibrium will change in a way that makes Q approach K:

• If Q = K, for example, then the system is already at equilibrium, and no further change in the composition of the system will occur unless the conditions are changed.
• If Q < K, then the ratio of the concentrations of products to the concentrations of reactants is less than the ratio at equilibrium. Therefore, the reaction will proceed to the right as written, forming products at the expense of reactants
• If Q > K, then the ratio of the concentrations of products to the concentrations of reactants is greater than at equilibrium, so the reaction will proceed to the left as written, forming reactants at the expense of products.

        These points are illustrated graphically in Figure 4.2.1.

Figure 4.2.1. (a) Both Q and K are plotted as points along a number line: the system will always react in the way that causes Q to approach K. (b) The change in the composition of a system with time is illustrated for systems with initial values of Q > K, Q < K, and Q = K.

Example 4.2.9 – Predicting the Direction of Reaction

Given here are the initial concentrations of reactants and products for three experiments involving this reaction:

CO (g) + H₂O (g)  ⇌ CO₂ (g) +  H₂ (g)

K_C = 0.64

Determine in which direction the reaction proceeds as it goes to equilibrium in each of the three experiments shown.

Solution

Experiment 1:

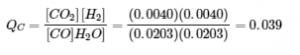
Q_c < K_c (0.039 < 0.64)

The reaction will shift to the right.

Experiment 2:

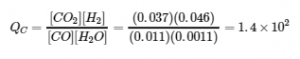
Q_c > K_c (140 > 0.64)

The reaction will shift to the left.

Experiment 3:

Q_c < K_c (0.48 < 0.64)

The reaction will shift to the right.

Check Your Learning 4.2.9 – Predicting the Direction of Reaction

Calculate the reaction quotient and determine the direction in which each of the following reactions will proceed to reach equilibrium.

(a) A 1.00-L flask containing 0.0500 mol of NO (g), 0.0155 mol of Cl₂ (g), and 0.500 mol of NOCl:

2 NO (g) + Cl₂ (g) ⇌ 2 NOCl (g)              Kc = 4.6 × 10⁴

(b) A 5.0-L flask containing 17 g of NH₃, 14 g of N₂, and 12 g of H₂:

N₂ (g) + 3 H₂ (g) ⇌ 2 NH₃ (g)          Kc = 0.060

(c) A 2.00-L flask containing 230 g of SO₃(g):

2 SO₃ (g) ⇌ 2 SO₂ (g) + O₂ (g)          Kc = 0.230

Answer

(a) Q_c = 6.45 × 10³, shifts right. (b) Q_c = 0.23, shifts left. (c) Q_c = 0, shifts right

Questions

★ Questions

1. Explain why an equilibrium between Br₂ (l) and Br₂ (g) would not be established if the container were not a closed vessel.
2. If you observe the following reaction at equilibrium, is it possible to tell whether the reaction started with pure NO₂ or with pure N₂O₄?

 2 NO₂ (g) ⇌ N₂O₄ (g)

   3. Among the solubility rules previously discussed is the statement: Carbonates, phosphates, borates, and arsenates—except those of the ammonium ion and the alkali metals—are insoluble.

a. Write the expression for the equilibrium constant for the reaction represented by the equation CaCO₃ (s) ⇌ Ca²⁺ (aq) + CO₃²⁻ (aq). Is K_c > 1, < 1, or ≈ 1? Explain your answer.

b. Write the expression for the equilibrium constant for the reaction represented by the equation 3 Ba²⁺ (aq) + 2 PO₄³⁻ (aq) ⇌ Ba₃(PO₄)₂ (s). Is K_c > 1, < 1, or ≈ 1? Explain your answer.

4. Benzene is one of the compounds used as octane enhancers in unleaded                 gasoline. It is manufactured by the catalytic conversion of acetylene to benzene: 3     C₂H₂ (g) ⟶ C₆H₆ (g). Which value of K_C would make this reaction most useful           commercially? K_C ≈ 0.01, K_C ≈ 1, or K_C ≈ 10. Explain your answer.

5. Show that the complete chemical equation, the total ionic equation, and the net ionic equation for the reaction represented by the equation KI (aq) + I₂ (aq)  ⇌ KI₃ (aq) give the same expression for the reaction quotient. KI₃ is composed of the ions K⁺ and I³⁻.

6. For a titration to be effective, the reaction must be rapid and the yield of the reaction must essentially be 100%. Is K_C > 1, < 1, or ≈ 1 for a titration reaction?

7. Write the mathematical expression for the reaction quotient, Q_C, for each of the following reactions:

a. CH₄ (g) + Cl₂ (g) ⇌ CH₃Cl (g) + HCl (g)

b. N₂ (g) + O₂ (g) ⇌ 2 NO (g)

c. 2 SO₂ (g) + O₂ (g) ⇌ 2 SO₃ (g)

d. BaSO₃ (s) ⇌ BaO (s) + SO₂ (g)

e. P₄ (g) + 5 O₂ (g) ⇌ P₄O₁₀ (s)

f. Br₂ (g) ⇌ 2Br (g)

g. CH₄ (g) + 2 O₂ (g) ⇌ CO₂ (g) + 2 H₂O (l)

h. CuSO₄ ∙ 5H₂O (s) ⇌ CuSO₄ (s) + 5 H₂O (g)

8. The initial concentrations or pressures of reactants and products are given for       each of the following systems. Calculate the reaction quotient and determine the     direction in which each system will proceed to reach equilibrium.

a. 2 NH₃ (g) ⇌ N₂ (g) + 3 H₂ (g)            Kc = 17; [NH3] = 0.20 mol/L, [N2] = 1.00               mol/L, [H2] = 1.00 mol/L

b. 2 NH₃ (g) ⇌ N₂ (g) + 3 H₂ (g)            K_P = 6.8 x 10⁴; initial pressures: NH₃ =                 2.00 atm, N₂ = 10.00 atm, H₂ = 10.00 atm

c. 2 SO₃ (g) ⇌ 2 SO₂ (g) +O₂ (g)     Kc = 0.230; [SO₃] = 2.00 mol/L, [SO₂] = 2.00               mol/L, [O₂] = 2.00 mol/L

d. 2 SO₃ (g) ⇌ 2 SO₂ (g) + O₂ (g)           K_P = 6.5 atm; initial pressures: SO₂ = 1.00           atm, O₂ = 1.130 atm, SO₃ = 0 atm

e. 2 NO (g) + Cl₂ (g) ⇌ 2 NOCl (g)     K_P = 2.5 x 10³; initial pressures: NO = 1.00               atm, Cl₂ = 1.00 atm, NOCl = 0 atm

f. N₂ (g) + O₂ (g) ⇌ 2 NO (g)          Kc = 0.050; [N₂] = 0.100 mol/L, [O₂] = 0.200               mol/L, [NO] = 1.00 mol/L

★★ Questions

   9. The following reaction has K_P = 4.50 × 10⁻⁵ at 720 K.

N₂ (g) + 3 H₂ (g) ⇌ 2NH₃ (g)

If a reaction vessel is filled with each gas to the partial pressures listed, in which direction will it shift to reach equilibrium? P(NH₃) = 93 atm, P(N₂) = 48 atm, and P(H₂) = 52

   10. Determine if the following system is at equilibrium. If not, in which direction will the system need to shift to reach equilibrium?

SO₂Cl₂ (g) ⇌ SO₂ (g) + Cl₂ (g)

[SO₂Cl₂] = 0.12 mol/L, [Cl₂] = 0.16 mol/L and [SO₂] = 0.050 mol/l. K_c for the reaction is 0.078.

   11. Which of the systems described in question 8 give homogeneous equilibria?         Which give heterogeneous equilibria?

12. For which of the reactions in question 8 does K_C (calculated using                           concentrations) equal K_P (calculated using pressures)?

13. Convert the values of K_C to values of K_P or the values of K_P to values of K_C.

a. N₂ (g) + 3 H₂ (g) ⇌ 2 NH₃ (g)                               K_C = 0.50 at 400◦C

b. H₂ (g) + I₂ (g) ⇌ 2 HI (g)                                               K_C = 50.2 at 448◦C

c. Na₂SO₄ ∙ 10H₂O (s) ⇌ Na₂SO₄ (s) + 10 H₂O (g)           K_P = 4.08 x 10^-25 at  25◦C

d. H₂O (l) ⇌ H₂O (g)                                             K_P = 0.122 at 50◦C

14. What is the value of the equilibrium constant expression for the change H₂O (l) ⇌ H₂O (g) at 30 °C? (See Appendix F.)

15. Write the expression of the reaction quotient for the ionization of HOCN in water.

16. Write the reaction quotient expression for the ionization of NH₃ in water.

17. What is the approximate value of the equilibrium constant K_P for the change C₂H₅OC₂H₅ (l) ⇌ C₂H₅OC₂H₅ (g) at 25 °C. (Vapor pressure was described in the previous chapter on liquids and solids; refer back to this chapter to find the relevant information needed to solve this problem.)

Answers

   1. Equilibrium cannot be established between the liquid and the gas phase if the top is removed from the bottle because the system is not closed; one of the components of the equilibrium, the Br₂ vapor, would escape from the bottle until all liquid disappeared. Thus, more liquid would evaporate than can condense back from the gas phase to the liquid phase.

   2. Yes, based on the changing of colours in the reaction it is possible to determine     the direction of the reaction.

   3. (a) K_C = [Ca²⁺][CO₃^2-], K_C < 1 ;(b) K_C = 1 /  [Ba²⁺]³[PO₄^3-]², K_C > 1

   4. Since , a value of K_C ≈ 10 means that C₆H₆ predominates over C₂H₂. In such a case, the reaction would be commercially feasible if the rate to equilibrium is suitable.

   5. Total Ionic: K⁺ (aq) + I⁻ (aq) + I₂ (aq) ⇌ K⁺ (aq) + I₃⁻ (aq), Net Ionic:  I⁻ (aq) + I₂  (aq) ⇌ I₃⁻ (aq)

   6. K_C > 1

     

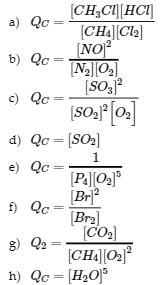
8. (a) Q_c 25 proceeds left; (b) Q_P 0.22 proceeds right; (c) Q_c undefined proceeds left; (d) Q_P 1.00 proceeds right; (e) Q_P 0 proceeds right; (f) Q_c 4 proceeds left

9. The system will shift toward the reactants to reach equilibrium.

10. The system is not at equilibrium since Q < K, therefore the reaction will shift         towards the right.

11. (a) Homogeneous, (b) Homogeneous, (c) Homogeneous, (d) Homogeneous, (e)     Homogeneous, (f) Homogeneous

12. F is the only one where K_c = K_P

13. (a) K_P = 1.6 × 10⁻⁴; (b) K_P = 50.2; (c) K_c = 5.31 × 10⁻³⁹; (d) K_c = 4.60 × 10⁻³

14. K_P = P_H2O = 0.042.

   15.

   16.

17. 0.717 atm