4.4 – Le Châtelier’s Principle
As you already know by now about equilibrium reactions, reactions proceed in both directions (reactants go to products and products go to reactants). We can tell a reaction is at equilibrium if the reaction quotient (Q) is equal to the equilibrium constant (K). We next address what happens when a system at equilibrium is disturbed so that Q is no longer equal to K. If a system at equilibrium is subjected to a perturbation or stress (such as a change in concentration) the position of equilibrium changes. Since this stress affects the concentrations of the reactants and the products, the value of Q will no longer equal the value of K. To re-establish equilibrium, the system will either shift toward the products (if Q < K) or the reactants (if Q > K) until Q returns to the same value as K.
This process is described by Le Châtelier's principle: When a chemical system at equilibrium is disturbed, it returns to equilibrium by counteracting the disturbance. As described in the previous paragraph, the disturbance causes a change in Q; the reaction will shift to re-establish Q = K.
Predicting the Direction of a Reversible Reaction
Le Châtelier’s principle can be used to predict changes in equilibrium concentrations when a system that is at equilibrium is subjected to a stress. However, if we have a mixture of reactants and products that have not yet reached equilibrium, the changes necessary to reach equilibrium may not be so obvious. In such a case, we can compare the values of Q and K for the system to predict the changes.
Effect of Change in Concentration on Equilibrium
A chemical system at equilibrium can be temporarily shifted out of equilibrium by adding or removing one or more of the reactants or products. The concentrations of both reactants and products then undergo additional changes to return the system to equilibrium. This is illistrated in Figure 4.4.1:

Figure 4.4.1. a) The test tube contains 0.1 M Fe3+. (b) Thiocyanate ion has been added to solution in (a), forming the red Fe(SCN)2+ ion, according to the chemical equilibrium: Fe3+(aq) + SCN−(aq) ⇌ Fe(SCN)2+(aq). (c) Silver nitrate has been added to the solution in (b), precipitating some of the SCN− as the white solid AgSCN, according to: Ag+(aq) + SCN−(aq) → AgSCN(s). The decrease in the SCN− concentration shifts the first equilibrium in the solution to the left, decreasing the concentration (and lightening color) of the Fe(SCN)2+. (credit: modification of work by Mark Ott)
The stress on the system in Figure 4.4.1 is the reduction of the equilibrium concentration of SCN−: lowering the concentration of this reactant would cause Q to be larger than K. As a consequence, Le Châtelier’s principle leads us to predict that the concentration of Fe(SCN)2+ should decrease, increasing the concentration of SCN− part way back to its original concentration, and increasing the concentration of Fe3+ above its initial equilibrium concentration.
The effect of a change in concentration on a system at equilibrium is illustrated further by the equilibrium of this chemical reaction:
H2 (g) + I2 (g) ⇌ 2 HI (g) KC = 50.0 at 400°C
The numeric values for this example have been determined experimentally. A mixture of gases at 400°C with [H2] = [I2] = 0.221 M and [HI] = 1.563 M is at equilibrium; for this mixture, Qc = KC = 50.0. If H2 is introduced into the system so quickly that its concentration doubles instantaneously (new [H2] = 0.442 M), the reaction will shift so that a new equilibrium is reached, at which [H2] = 0.374 M, [I2] = 0.153 M, and [HI] = 1.692 M. This gives:
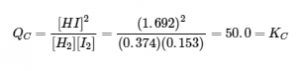
We have stressed this system by introducing additional H2. The stress is relieved when the reaction shifts to the right, using up some (but not all) of the excess H2, reducing the amount of uncombined I2, and forming additional HI.
Effect of Change in Pressure/Volume on Equilibrium
Sometimes we can change the position of equilibrium by changing the pressure of a system. However, changes in pressure have a measurable effect only in systems in which gases are involved, and then only when the chemical reaction produces a change in the total number of gas molecules in the system. An easy way to recognize such a system is to look for different numbers of moles of gas on the reactant and product sides of the equilibrium. While evaluating pressure (as well as related factors like volume), it is important to remember that equilibrium constants are defined with regard to concentration (for KC) or partial pressure (for KP). Some changes to total pressure, like adding an inert gas that is not part of the equilibrium, will change the total pressure but not the partial pressures of the individual gases in the equilibrium constant expression. Thus, addition of a gas not involved in the equilibrium will not perturb the equilibrium.
As we increase the pressure of a gaseous system at equilibrium, either by decreasing the volume of the system or by adding more of one of the components of the equilibrium mixture, we introduce a stress by increasing the partial pressures of one or more of the components. In accordance with Le Châtelier’s principle, a shift in the equilibrium that reduces the total number of molecules per unit of volume will be favored because this relieves the stress. The reverse reaction would be favored by a decrease in pressure.
Consider what happens when we increase the pressure on a system in which NO, O2, and NO2 are at equilibrium:
2 NO (g) + O2 (g) ⇌ 2 NO2 (g)
The formation of additional amounts of NO2 decreases the total number of molecules in the system because each time two molecules of NO2 form, a total of three molecules of reactants (NO and O2) are consumed. This reduces the total pressure exerted by the system and reduces, but does not completely relieve, the stress of the increased pressure. On the other hand, a decrease in the pressure on the system favors decomposition of NO2 into NO and O2, which tends to restore the pressure.
Now consider this reaction:
N2 (g) + O2 (g) ⇌ 2 NO (g)
Because there is no change in the total number of molecules in the system during reaction, a change in pressure does not favor either formation or decomposition of gaseous nitrogen monoxide.
|
Effect of Change in Pressure on Equilibrium – Video Demonstration |
|
Check out this cool video to observe the colour change that happens when pressure is applied to an equilibrium mixture of NO2 (brown) and N2O4 (colourless). N2O4 (g) ⇌ 2 NO2 (g) Notice how sometime after the pressure is applied, the colour of the mixture lightens – if we think about this using Le Châtelier’s Principle, the increase of pressure is the stress that needs to be offset by decreasing the pressure in the system – this can be achieved by reducing the number of moles of gas in the system. This means that the reaction to the left is driven forward, where molecules of NO2 react to form more N2O4 which is colourless and hence gives the mixture a lighter colour (i.e. increased extent of colourlessness). |
Effect of Change in Temperature on Equilibrium
Changing concentration or pressure perturbs an equilibrium because the reaction quotient is shifted away from the equilibrium value. Changing the temperature of a system at equilibrium has a different effect: A change in temperature actually changes the value of the equilibrium constant. However, we can qualitatively predict the effect of the temperature change by treating it as a stress on the system and applying Le Châtelier’s principle.
When hydrogen reacts with gaseous iodine, heat is evolved/released.
H2 (g) + I2 (g) ⇌ 2 HI (g) ΔH = -9.4 kJ (exothermic)
Because this reaction is exothermic, we can write it with heat as a product.
H2 (g) + I2 (g) ⇌ 2 HI (g) + heat
Increasing the temperature of the reaction increases the internal energy of the system. Thus, increasing the temperature has the effect of increasing the amount of one of the products of this reaction. The reaction shifts to the left to relieve the stress, and there is an increase in the concentration of H2 and I2 and a reduction in the concentration of HI. Lowering the temperature of this system reduces the amount of energy present, favours the production of heat, and favours the formation of hydrogen iodide.
When we change the temperature of a system at equilibrium, the equilibrium constant for the reaction changes. Lowering the temperature in the HI system increases the equilibrium constant: At the new equilibrium the concentration of HI has increased and the concentrations of H2 and I2 decreased. Raising the temperature decreases the value of the equilibrium constant, from 67.5 at 357 °C to 50.0 at 400 °C. Temperature affects the equilibrium between NO2 and N2O4 in this reaction:
N2O4 (g) ⇌ 2 NO2 (g) ΔH = 57.20 kJ
The positive ΔH value tells us that the reaction is endothermic and could be written as:
Heat + N2O4 (g) ⇌ 2 NO2 (g)
At higher temperatures, the gas mixture has a deep brown color, indicative of a significant amount of brown NO2 molecules. If, however, we put a stress on the system by cooling the mixture (withdrawing energy), the equilibrium shifts to the left to supply some of the energy lost by cooling. The concentration of colorless N2O4 increases, and the concentration of brown NO2 decreases, causing the brown color to fade.
Temperature Dependence of K
As we’ve just recently noted, temperature is special in that it actually affects the value of the equilibrium constant for a reaction. Hence, equilibrium constants are temperature dependent. This relationship, which also relates K and the standard enthalpies and entropies, is known as the Van’t Hoff equation. It is expressed as

Figure 4.4.1 K Relation to Enthalpies
where
- K is the equilibrium constant
- ΔH° is the standard enthalpy change, in units of energy (e.g. J)
- R is the gas constant (as seen in the gases unit) expressed in units of energy per Kelvin (e.g. J/K)
- T is the temperature in Kelvin
ΔSº is a thermodynamic property just like enthalpy (ΔHº), known as the standard change in entropy (S), expressed in units of energy per Kelvin (e.g. J/K). This topic is beyond the scope of this course (instead, you will learn about entropy in detail in your 2nd-year physical chemistry course), but for now, all you need to know is that it is a measure of the dispersal or distribution of matter and/or energy in a system, and it is often described as representing the “disorder” of the system. The greater the disorder in a system, the greater the entropy. For example, the entropy of a gas is greater than that of a liquid, and the entropy of a liquid is greater than that of a solid. In addition, heating substances increases the disorder of its constituent particles and hence increases their entropy.
Looking at the equation above, notice how it can be formatted in the form y = mx + b. This gives us a linear relationship between ln K (y) and 1/T (x). Consequently, the thermodynamic enthalpy and entropy changes (∆Hº and ∆Sº) for a reversible reaction can be determined from plotting ln K vs. 1/T data without the aid of calorimetry. The plot of ln K vs. 1/T shows that it should be a line with slope −ΔHo/R (this represents m) and intercept ΔSo/R (this represents b). Of course, the main assumption here is that only K is dependent on T; ΔHo and ΔSo are only very weakly dependent on T, which is usually valid over a narrow temperature range.
Assuming ΔH° and ΔS° are temperature independent, for an exothermic reaction (ΔH° < 0), the slope of the graph is positive and the magnitude of ln K increases with increasing temperature, whereas for an endothermic reaction (ΔH° > 0), the slope of the graph is negative and the magnitude of ln K decreases with increasing temperature (Figure 4.4.2).
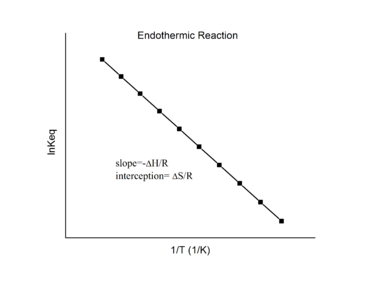
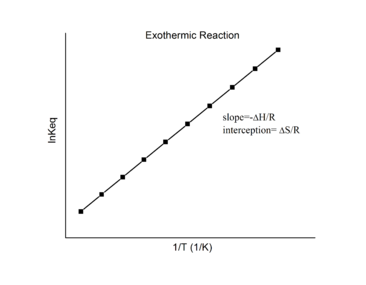
Figure 4.4.2. Endothermic reaction (left) and exothermic reaction van’t Hoff plots (right). (CC BY-SA 3.0)
The quantitative relationship expressed in the van’t Hoff equation agrees with the qualitative predictions made by applying Le Châtelier’s principle. Because heat is produced in an exothermic reaction, adding heat (by increasing the temperature) will shift the equilibrium to the left, favoring the reactants and decreasing the magnitude of K. Conversely, because heat is consumed in an endothermic reaction, adding heat will shift the equilibrium to the right, favoring the products and increasing the magnitude of K. The van’t Hoff equation also shows that the magnitude of ΔH° dictates how rapidly K changes as a function of temperature. In contrast, the magnitude and sign of ΔS° affect the magnitude of K but not its temperature dependence.
If we know the value of K at a given temperature and the value of ΔH° for a reaction, we can estimate the value of K at any other temperature, even in the absence of information on ΔS°. Suppose, for example, that K1 and K2 are the equilibrium constants for a reaction at temperatures T1 and T2, respectively. Applying the van’t Hoff equation gives the following relationship at each temperature:
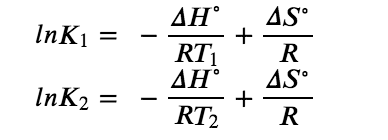
Subtracting ln K1 from ln K2 we get:
![]()
This modified van’t Hoff equation is one we’ll call the “two-point van’t Hoff equation.” Hence, by calculating ΔH° from tabulated enthalpies of formation and measuring the equilibrium constant at one temperature (K1), we can calculate the value of the equilibrium constant at any other temperature (K2), assuming that ΔH° and ΔS° are independent of temperature. There are also a few other points to consider when using the two-point van’t Hoff equation – see the note below.
|
NOTE: |
|
To determine the most accurate values for ΔH° and ΔS° for a particular reaction in an experimental setting, a good scientist would measure multiple values of K at different temperatures to collect many data points. This allows them to visualize a more accurate relationship between ln K and 1/T in a van’t Hoff plot. If the scientist is in a hurry, collecting just two data points and using the two-point version of the van’t Hoff equation should still suffice in most cases. In order to work, however, we must assume that the relationship between ln K and 1/T is perfectly linear between the two temperatures T1 and T2. This linearity is usually the case when both temperatures are relatively close to one another, but it breaks down the further apart the two temperatures are. |
Example 4.4.1 – Using the van’t Hoff Equation
The equilibrium constant for the formation of NH3 from H2 and N2 at 25°C is KP = 5.4 × 105. What is KP at 500°C? (ΔHº = -91.8 kJ)
Solution:
If we set T1 = 25°C = 298 K and T2 = 500°C = 773 K, then using van’t Hoff’s equation we obtain the following:
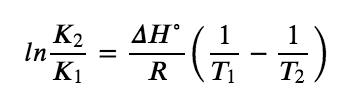
Thus at 500°C, the equilibrium strongly favors the reactants over the products.
Check Your Learning 4.4.1 – Using the van’t Hoff Equation
You calculate KP = 2.2 × 1012 for the reaction of NO with O2 to give NO2 at 25°C. Use the ΔHf° values provided in Appendix G to calculate KP for this reaction at 1000°C.
Answer:
5.6 × 10−4
Effect of Catalysts on Equilibrium
As we’ll learn later on and in greater depth during our study of kinetics, a catalyst accelerates the rate of a reaction and is consumed then regenerated in the process. Catalysts function by providing an alternate reaction mechanism that has a lower activation energy than would be found in the absence of the catalyst. Note the definition of activation energy: it is the minimum amount of energy required for a chemical reaction to proceed either in the forward direction from reactants to products, or in the reverse direction for products to reactants.
This lowered activation energy by a catalyst results in an increase in rate as described by the Arrhenius equation (which we’ll cover in detail in Chapter 7: Chemical Kinetics). Note that a catalyst decreases the activation energy for both the forward and the reverse reactions and hence accelerates both the forward and the reverse reactions. Consequently, the presence of a catalyst will permit a system to reach equilibrium more quickly, but it has no effect on the position of the equilibrium as reflected in the value of its equilibrium constant.
|
|
An Application of Equilibrium Concepts – The Haber Process
The interplay of changes in concentration or pressure, temperature, and the presence of a catalyst on a chemical equilibrium is illustrated in the industrial synthesis of ammonia from nitrogen and hydrogen according to the equation:
N2 (g) + 3 H2 (g) ⇌ 2 NH3 (g)
A large quantity of ammonia is manufactured by this reaction. Each year, ammonia is among the top 10 chemicals, by mass, manufactured in the world. About 2 billion pounds are manufactured in the United States each year. Ammonia plays a vital role in our global economy. It is used in the production of fertilizers and is, itself, an important fertilizer for the growth of corn, cotton, and other crops. Large quantities of ammonia are converted to nitric acid, which plays an important role in the production of fertilizers, explosives, plastics, dyes, and fibers, and is also used in the steel industry.
It has long been known that nitrogen and hydrogen react to form ammonia. However, it became possible to manufacture ammonia in useful quantities by the reaction of nitrogen and hydrogen only in the early 20th century after the factors that influence its equilibrium were understood.
To be practical, an industrial process must give a large yield of product relatively quickly. One way to increase the yield of ammonia is to increase the pressure on the system in which N2, H2, and NH3 are at equilibrium or are coming to equilibrium.
N2 (g) + 3 H2 (g) ⇌ 2 NH3 (g)
The formation of additional amounts of ammonia reduces the total pressure exerted by the system and somewhat reduces the stress of the increased pressure.
Although increasing the pressure of a mixture of N2, H2, and NH3 will increase the yield of ammonia, at low temperatures, the rate of formation of ammonia is slow. At room temperature, for example, the reaction is so slow that if we prepared a mixture of N2 and H2, no detectable amount of ammonia would form during our lifetime. The formation of ammonia from hydrogen and nitrogen is an exothermic process:
N2 (g) + 3 H2 (g) ⇌ 2 NH3 (g) ΔHº = -92.2 kJ
Thus, increasing the temperature to increase the rate lowers the yield. If we lower the temperature to shift the equilibrium to favour the formation of more ammonia, equilibrium is reached more slowly because of the large decrease of reaction rate with decreasing temperature.
Part of the rate of formation lost by operating at lower temperatures can be recovered by using a catalyst. The net effect of the catalyst on the reaction is to cause equilibrium to be reached more rapidly.
In the commercial production of ammonia, conditions of about 500 °C, 150–900 atm, and the presence of a catalyst are used to give the best compromise among rate, yield, and the cost of the equipment necessary to produce and contain high-pressure gases at high temperatures (Figure 4.4.3).
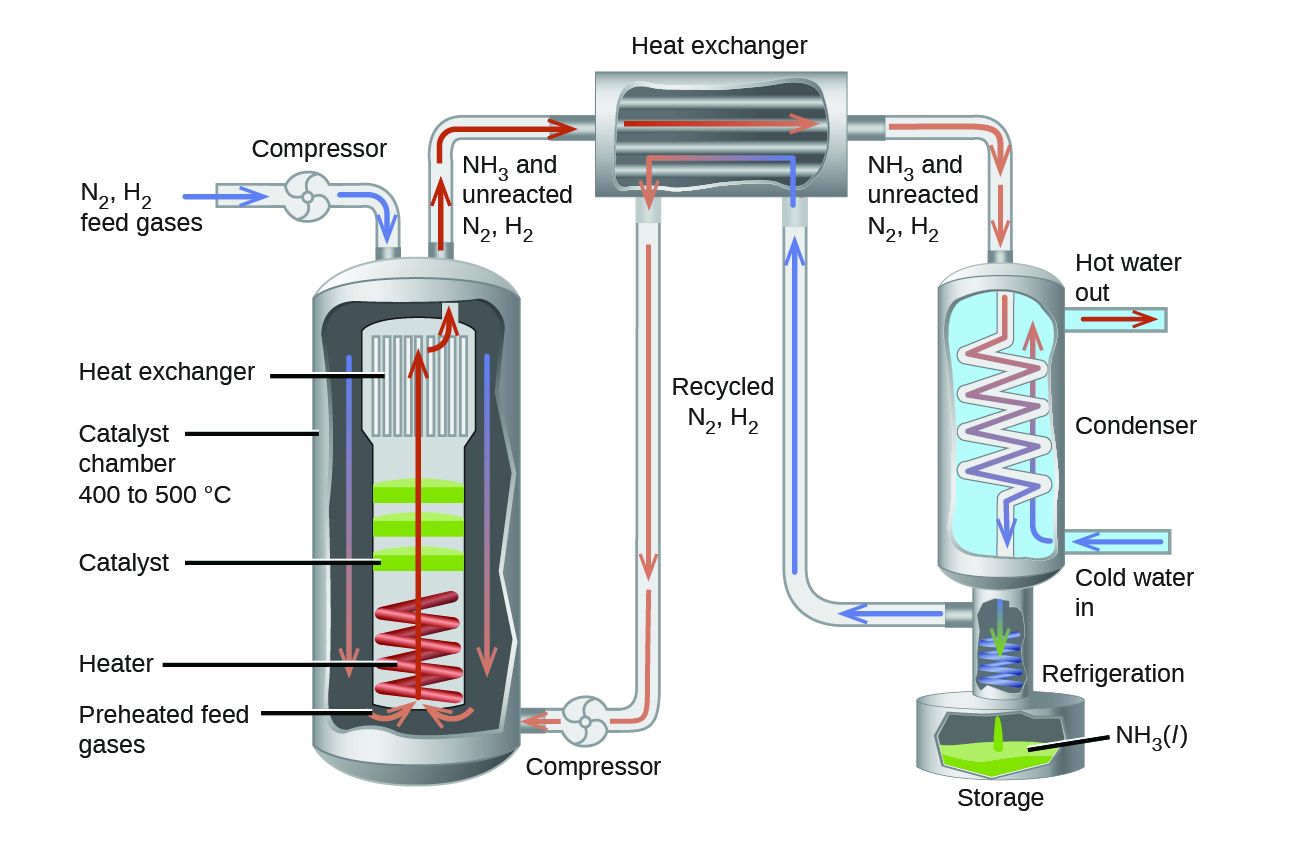
Figure 4.4.3. Commercial production of ammonia requires heavy equipment to handle the high temperatures and pressures required. This schematic outlines the design of an ammonia plant.
Summary – Le Châtelier’s Principle
The following table summarizes how each disturbance will restore equilibrium in the system and its effect (if applicable) on K.
Table 4.4.1 Effects of Disturbances of Equilibrium and K
|
Effects of Disturbances of Equilibrium and K |
|||
|
Disturbance |
Observed Change as Equilibrium is Restored |
Direction of Shift |
Effect on K |
|
reactant added |
added reactant is partially consumed |
toward products |
none |
|
product added |
added product is partially consumed |
toward reactants |
none |
|
decrease in volume/increase in gas pressure |
pressure decreases |
toward side with fewer moles of gas |
none |
|
increase in volume/decrease in gas pressure |
pressure increases |
toward side with more moles of gas |
none |
|
temperature increase |
heat is absorbed |
toward products for endothermic, toward reactants for exothermic |
changes |
|
temperature decrease |
heat is given off |
toward reactants for endothermic, toward products for exothermic |
changes |
Example 4.4.2 – Qualitative Predictions of Equilibrium Shifts – 1
Consider the following reaction:
2 SO2 (g) + O2 (g) ⇌ 2 SO3 (g)∆Hº < 0
Explain how each of the following will affect the amount of SO3 (g):
(a) Increase in pressure
(b) Increase in temperature
(c) Increase in the amount of O2 (g)
Solution
(a) There are three moles of gas on the reactants side and only two moles of gas on the products side. The equilibrium position will shift to decrease the total pressure exerted by the system and counteract the stress of the increase in pressure. Having fewer moles of gas present decreases the pressure. Therefore, the forward reaction is favoured, and the amount of SO3 (g) will increase.
(b) ∆Hº < 0, so the reaction is exothermic and hence produces heat and we can rewrite the chemical equilibrium equation as follows:
2 SO2 (g) + O2 (g) ⇌ 2 SO3 (g) + heat
The equilibrium position will shift to counteract the increase in temperature by removing heat from the system. Therefore, the reverse reaction is favoured to yield more reactants, and correspondingly the amount of SO3(g) will decrease.
(c) The equilibrium position will shift to decrease the amount of O2(g) present to counteract the increase in O2(g). Using up excess O2(g) is favoured to decrease its amount in the system. Therefore, the forward reaction is favoured to yield more product, and the amount of SO3(g) will increase.
Check Your Learning 4.4.2 – Qualitative Predictions of Equilibrium Shifts – 1
Given the following situations, determine what will happen to the amount of H2 that will be present in an equilibrium mixture in the reaction
3 Fe (s) + 4 H2O (g) ⇌ Fe3O4 (s) + 4 H2 (g) ∆H° = -150 kJ
(a) Decreasing the temperature of the mixture
(b) Introducing more Fe(s)
(c) Halving the volume of the container
(d) Adding a catalyst
Answer
(a) amount of H2(g) will increase; (b) no change in the amount of H2(g) (recall that solids and pure liquids have activities equal to 1 and thus have no influence on an equilibrium’s position!); (c) no change in the amount of H2(g); (d) no change in the amount of H2(g)
Check Your Learning 4.4.3 – Qualitative Predictions of Equilibrium Shifts – 2
Consider the equilibrium reaction
A (g) + ½ B (g) ⇌ 2 C (g)∆H° = -52 kJ
Which of the following options would be most effective at encouraging the forward reaction?
(a) Remove C + add heat
(b) Increase volume + add heat
(c) Add C + remove heat
(d) Decrease volume + add heat
(e) Increase volume + add A
(f) Remove B + remove heat
Answer
(e) Increase volume + add A
|
In Case You’re Interested…Equilibria in the Garden |
|
Hydrangeas are common flowering plants around the world. Although many hydrangeas are white, there is one common species (Hydrangea macrophylla) whose flowers can be either red or blue, as shown in the accompanying figure. How is it that a plant can have different colored flowers like this?
Figure 4.4.4. This species of hydrangea has flowers that can be either red or blue. Why the color difference? Source: “Hydrangea” by Janne Moren is Licensed under the Creative Commons Attribution-NonCommercial-ShareAlike 2.0 Generic. Interestingly, the color of the flowers is due to the acidity of the soil that the hydrangea is planted in. An astute gardener can adjust the pH of the soil and actually change the color of the flowers. However, it is not the H3O+ or OH− ions themselves that affect the color of the flowers. Rather, it is the presence of aluminum ions that causes the color change. The solubility of various aluminum salts in soil—and thus the ability of plants to absorb the Al3+ ions —is dependent on the acidity of the soil. If the soil is relatively acidic, the aluminum is more soluble, and plants can absorb it more easily. Under these conditions, hydrangea flowers are blue as Al ions interact with anthocyanin pigments in the plant. In more basic soils, aluminum is less soluble, and under these conditions the hydrangea flowers are red. Gardeners who change the pH of their soils to change the color of their hydrangea flowers are therefore employing Le Chatelier’s principle: the amount of acid in the soil changes the equilibrium of aluminum solubility, which in turn affects the color of the flowers. We will examine the effect of pH on salt solubility in more detail in Chapter 6. |
Questions
★ Questions
1. The following equation represents a reversible decomposition:
CaCO3 (s) ⇌ CaO (s) + CO2 (g)
Under what conditions will decomposition in a closed container proceed to completion so that no CaCO3 remains?
2. Explain how to recognize the conditions under which changes in pressure would affect systems at equilibrium.
3. What property of a reaction can we use to predict the effect of a change in temperature on the value of an equilibrium constant?
4. What would happen to the color of the solution in part (b) of Figure 4.4.1. if a small amount of NaOH were added and Fe(OH)3 precipitated? Explain your answer.
5. The following reaction occurs when a burner on a gas stove is lit:
CH4 (g) + 2 O2 (g) ⇌ CO2 (g) + 2 H2O (g)
Is an equilibrium among CH4, O2, CO2, and H2O established under these conditions? Explain your answer.
6. A necessary step in the manufacture of sulfuric acid is the formation of sulfur trioxide, SO3, from sulfur dioxide, SO2, and oxygen, O2, shown here. At high temperatures, the rate of formation of SO3 is higher, but the equilibrium amount (concentration or partial pressure) of SO3 is lower than it would be at lower temperatures.
SO2 (g) + O2 (g) ⇌ 2 SO3 (g)
a. Does the equilibrium constant for the reaction increase, decrease, or remain about the same as the temperature increases?
b. Is the reaction endothermic or exothermic?
7. Suggest four ways in which the concentration of hydrazine, N2H4, could be increased in an equilibrium described by the following equation:
N2 (g) + 2 H2 (g) ⇌ N2H4 (g) ΔH = 95 kJ
8. Suggest four ways in which the concentration of PH3 could be increased in an equilibrium described by the following equation:
P4 (g) + 6 H2 (g) ⇌ 4 PH3 (g) ΔH = 110.5 kJ
9. How will an increase in temperature affect each of the following equilibria? How will a decrease in the volume of the reaction vessel affect each?
a. 2 H2O (g) ⇌ 2 H2 (g) + O2 (g) ΔH = 484 kJ
b. N2 (g) + 3 H2 (g) ⇌ 2 NH3 (g) ΔH = -92.2 kJ
c. 2 Br (g) ⇌ Br2 (g) ΔH = -224 kJ
d. H2 (g) + I2 (s) ⇌ 2 HI (g) ΔH = 53 kJ
★★ Questions
10. Water gas is a 1:1 mixture of carbon monoxide and hydrogen gas and is called water gas because it is formed from steam and hot carbon in the following reaction: H2O (g) + C (s) ⇌ H2 (g) + CO (g). Methanol, a liquid fuel that could possibly replace gasoline, can be prepared from water gas and hydrogen at high temperature and pressure in the presence of a suitable catalyst.
a. Write the expression for the equilibrium constant (KC) for the reversible reaction
2 H2 (g) + CO (g) ⇌ CH3OH (g) ΔH = -90.2 kJ
b. What will happen to the concentrations of H2, CO, and CH3OH at equilibrium if more H2 is added?
c. What will happen to the concentrations of H2, CO, and CH3OH at equilibrium if CO is removed?
d. What will happen to the concentrations of H2, CO, and CH3OH at equilibrium if CH3OH is added?
e. What will happen to the concentrations of H2, CO, and CH3OH at equilibrium if the temperature of the system is increased?
f. What will happen to the concentrations of H2, CO, and CH3OH at equilibrium if more catalyst is added?
11. Pure iron metal can be produced by the reduction of iron(III) oxide with hydrogen gas.
a. Write the expression for the equilibrium constant (KC) for the reversible reaction
Fe2O3 (s) + 3 H2 (g) ⇌ 2 Fe (s) + 3 H2O (g) ΔH = 98.7 kJ
b. What will happen to the concentration of each reactant and product at equilibrium if more Fe is added?
c. What will happen to the concentration of each reactant and product at equilibrium if H2O is removed?
d. What will happen to the concentration of each reactant and product at equilibrium if H2 is added?
e. What will happen to the concentration of each reactant and product at equilibrium if the pressure on the system is increased by reducing the volume of the reaction vessel?
f. What will happen to the concentration of each reactant and product at equilibrium if the temperature of the system is increased?
12. Acetic acid is a weak acid that reacts with water according to this equation:
CH3CO2H (aq) + H2O (aq) ⇌ H3O– (aq) + CH3CO2 (aq)
Will any of the following increase the percent of acetic acid that reacts and produces CH3CO2− ion?
a. Addition of HCl
b. Addition of NaOH
c. Addition of NaCH3CO2
13. Suggest two ways in which the equilibrium concentration of Ag+ can be reduced in a solution of Na+, Cl−, Ag+, and NO3−, in contact with solid AgCl.
Na+ (aq) + Cl– (aq) + Ag+ (aq) + NO3– (aq) ⇌ AgCl (s) + Na+ (aq) + NO3– (aq)
ΔH = – 65.9 kJ
14. How can the pressure of water vapor be increased in the following equilibrium?
H2O (l) ⇌ H2O (g) ΔH = 41 kJ
15. Additional solid silver sulfate, a slightly soluble solid, is added to a solution of silver ion and sulfate ion at equilibrium with solid silver sulfate.
2 Ag+ (aq) + SO42- (aq) ⇌ Ag2SO4 (s)
Which of the following will occur?
a. Ag+ or SO42− concentrations will not change.
b. The added silver sulfate will dissolve.
c. Additional silver sulfate will form and precipitate from solution as Ag+ ions and SO42− ions combine.
d. The Ag+ ion concentration will increase and the SO42− ion concentration will decrease.
16. The amino acid alanine has two isomers, α-alanine and β-alanine. When equal masses of these two compounds are dissolved in equal amounts of a solvent, the solution of α-alanine freezes at the lowest temperature. Which form, α-alanine or β-alanine, has the larger equilibrium constant for ionization (HX ⇌ H+ + X−)?
Answers
1. The amount of CaCO3 must be so small that PCO2 is less than KP when the CaCO3 has completely decomposed. In other words, the starting amount of CaCO3 cannot completely generate the full PCO2 required for equilibrium.
2. When there is an unequal amount of gases in the products compared to the reactants would have an effect on the system at equilibrium.
3. The change in enthalpy may be used. If the reaction is exothermic, the heat produced can be thought of as a product. If the reaction is endothermic the heat added can be thought of as a reactant. Additional heat would shift an exothermic reaction back to the reactants but would shift an endothermic reaction to the products. Cooling an exothermic reaction causes the reaction to shift toward the product side; cooling an endothermic reaction would cause it to shift to the reactants’ side.
4. The SCN– would start being removed from reaction, and the system would shift towards the reactants. Solution will begin to look like solution (a).
5. No, it is not at equilibrium. Because the system is not confined, products continuously escape from the region of the flame; reactants are also added continuously from the burner and surrounding atmosphere.
6. (a) As the temperature increase, P ∝ T, pressure increases and the reaction shifts towards the products decreasing the equilibrium constant, (b) Exothermic
7. Add N2; add H2; decrease the container volume; heat the mixture.
8. Increase temperature, Increase pressure, Introduce more hydrogen gas, Decrease Volume, removal of PH3
9. (a) (i) shift to the right, (ii) shift to the left, (b) (i)shift to the left, (ii) shift to the right, (c) (i) shift to the left, (ii) shift to the right, (d) (i) shift to the right, (ii) shift to the left
10.
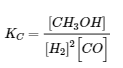
b. [H2] increases, [CO] decreases, [CH3OH] increases
c. [H2] increases, [CO] decreases, [CH3OH] decreases
d. [H2] increases, [CO] increases, [CH3OH] increases
e. [H2] increases, [CO] increases, [CH3OH] decreases
f. no changes
11. (a) KC = [H2O]3 / [H2]3, (b) no effect, (c) shift towards the products, (d) shift towards the products, (e) reaction is not affected by pressure, (f) shift towards the products
12. B
13. Add NaCl or some other salt that produces Cl− to the solution. Cooling the solution forces the equilibrium to the right, precipitating more AgCl (s).
14. Decrease the temperature
15. A
16. α-alanine
An equilibrium subjected to stress will shift in a way to counter the stress and re-establish equilibrium
Linear relation between ln K and the standard enthalpies and entropies, describing the temperature dependence of the equilibrium constant
Level of randomness (or disorder) of a system, or a measure of the energy dispersal of the molecules in the system



