6.4 – Equilibria of Slightly Soluble Ionic Compounds
Solubility
When a solid substance is mixed with a solvent in order to form a solution, there are several possible results. The determining factor for the result is the solubility of the substance, which is defined as the maximum possible concentration of the solute. The solubility rules help determine which substances are soluble, and to what extent.
Solubility Effects on Reactions
Depending on the solubility of a solute, there are three possible results: 1) if the solution has less solute than the maximum amount that it is able to dissolve (its solubility), it is a dilute unsaturated solution; 2) if the amount of solute is exactly the same amount as its solubility, it is saturated; 3) if there is more solute than is able to be dissolved, it is said to be supersaturated and the excess solute separates from the solution. If this separation process includes crystallization, it forms a precipitate. Precipitation lowers the concentration of the solute to the saturation in order to increase the stability of the solution.
We can use the following general rules for predicting the relative solubility of many ionic compounds:
Solubility Rules
1. Salts containing Group I elements (Li+, Na+, K+, Cs+, Rb+) are soluble. There are few exceptions to this rule. Salts containing the ammonium ion (NH4+) are also soluble.
2. Salts containing nitrate ion (NO3–) are generally soluble.
3. Salts containing Cl–, Br–, or I– are generally soluble. Important exceptions to this rule are halide salts of Ag+, Pb2+, and (Hg2)2+. Thus, AgCl, PbBr2, and Hg2Cl2 are insoluble.
4. Most silver salts are insoluble. AgNO3 and Ag(C2H3O2) are common soluble salts of silver; virtually all others are insoluble.
5. Most sulfate salts are soluble. Important exceptions to this rule include CaSO4, BaSO4, PbSO4, Ag2SO4 and SrSO4 .
6. Most hydroxide salts are only slightly soluble. Hydroxide salts of Group I elements are soluble. Hydroxide salts of Group II elements (Ca, Sr, and Ba) are slightly soluble. Hydroxide salts of transition metals and Al3+ are insoluble. Thus, Fe(OH)3, Al(OH)3, Co(OH)2 are not soluble.
7. Most sulfides of transition metals are highly insoluble, including CdS, FeS, ZnS, and Ag2S. Arsenic, antimony, bismuth, and lead sulfides are also insoluble.
8. Carbonates are frequently insoluble. Group II carbonates (CaCO3, SrCO3, and BaCO3) are insoluble, as are FeCO3 and PbCO3.
9. Chromates are frequently insoluble. Examples include PbCrO4 and BaCrO4.
10. Phosphates such as Ca3(PO4)2 and Ag3PO4 are frequently insoluble.
11. Fluorides such as BaF2, MgF2 and PbF2 are frequently insoluble.
Example 6.4.1 – Predicting Precipitation Reactions
Titration
Predict the result of mixing reasonably concentrated solutions of the following ionic compounds. If precipitation is expected, write a balanced net ionic equation for the reaction.
(a) Potassium sulfate and barium nitrate
(b) Lithium chloride and silver acetate
(c) Lead nitrate and ammonium carbonate
Solution
a) The two possible products for this combination are KNO3 and BaSO4. The solubility guidelines indicate BaSO4 is insoluble, and so a precipitation reaction is expected. The net ionic equation for this reaction, derived in the manner detailed in section 1.4, is:
Ba2+ (aq) + SO42- (aq) → BaSO4 (s)
b) The two possible products for this combination are LiC2H3O2 and AgCl. The solubility guidelines indicate AgCl is insoluble, and so a precipitation reaction is expected. The net ionic equation for this reaction, derived in the manner detailed in the previous module, is:
Ag+ (aq) + Cl– (aq) → AgCl (s)
c) The two possible products for this combination are PbCO3 and NH4NO3. The solubility guidelines indicate PbCO3 is insoluble, and so a precipitation reaction is expected. The net ionic equation for this reaction, derived in the manner detailed in the previous module, is:
Pb2+ (aq) + CO32- (aq) → PbCO3 (s)
Check Your Learning 6.4.1 – Predicting Precipitation Reactions
Predict the result of mixing reasonably concentrated solutions of the following ionic compounds. If precipitation is expected, write a balanced net ionic equation for the reaction.
(a) Calcium bromide and sodium carbonate
(b)Ammonium chromate and silver nitrate
(c) Cesium chloride and magnesium iodide
Answer
(a) Ca2+ (aq) + CO32– (aq) → CaCO3 (s)
(b) 2 Ag+ (aq) + CrO42– (aq) →Ag2CrO4 (s)
(c) No reaction (the two possible salts, cesium iodide and magnesium chloride, are soluble)
The Solubility Product Constant
By applying the above solubility rules, we can make qualitative predictions about precipitation reactions. However, these precipitates still exist in a dynamic equilibrium with aqueous ions, since these are technically sparingly (or slightly) soluble compounds that dissolve partially in aqueous solutions. For example, according to the solubility rules, silver chloride, AgCl, is classified as a sparingly soluble ionic solid (Figure 6.4.1). However, when we add an excess of solid AgCl to water, it dissolves to a small extent and produces a mixture consisting of a very dilute solution of Ag+ and Cl– ions in equilibrium with undissolved silver chloride:
AgCl (s) ⇌ Ag+ (aq) + Cl– (aq)
This equilibrium, like other equilibria, is dynamic; some of the solid AgCl is continuously dissolving, but at the same time, Ag+ and Cl– ions in the solution combine to produce an equal amount of the solid. At equilibrium, the opposing processes have equal rates, and macroscopically, the concentrations of dissolved ions and mass of remaining solid appear constant.
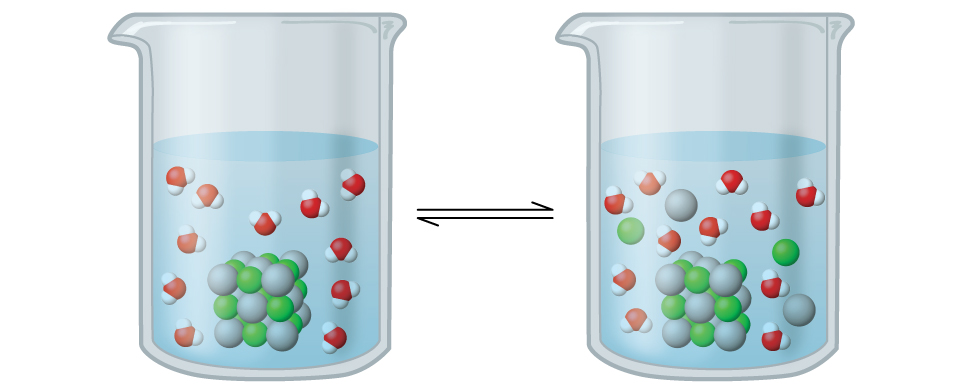
Figure 6.4.1. Silver chloride is a sparingly soluble ionic solid. When it is added to water, it dissolves slightly and produces a mixture consisting of a very dilute solution of Ag+ and Cl– ions in equilibrium with undissolved silver chloride.
The equilibrium constant for the equilibrium between a slightly soluble ionic solid and a solution of its ions is the solubility product (Ksp) of the solid. Recall from Chapter 4 that we use an ion’s concentration as an approximation of its activity in a dilute solution. For silver chloride, at equilibrium:
AgCl (s) ⇌ Ag+ (aq) + Cl– (aq)
When looking at dissolution reactions such as this, the solid is listed as a reactant, whereas the ions are listed as products. The solubility product constant, as with every equilibrium constant expression, is written as the product of the concentrations of each of the ions, raised to the power of their stoichiometric coefficients. Here, the solubility product constant is equal to [Ag+] x [Cl–] when a solution of silver chloride is in equilibrium with undissolved AgCl. There is no denominator representing the reactants in this equilibrium expression since the reactant is a pure solid; therefore [AgCl] does not appear in the expression for Ksp.
Some common solubility products are listed in Table 6.4.1, according to their Ksp values, whereas a more extensive compilation of products appears in Appendix L. Each of these equilibrium constants is much smaller than 1 because the compounds listed are only slightly soluble. A small Ksp represents a system in which the equilibrium lies to the left, so that relatively few hydrated ions would be present in a saturated solution.
Table 6.4.1 Common Solubility Products and their Equilibrium Constants
| Substance | Ksp at 25°C |
| CuCl | 1.2 × 10–6 |
| CuBr | 6.27 × 10-9 |
| AgI | 1.5 × 10-16 |
| PbS | 7 × 10-29 |
| Al(OH)3 | 2 × 10-32 |
| Fe(OH)3 | 4 × 10-38 |
Example 6.4.2 – Writing Equations and Solubility Products
Write the ionic equation for the dissolution and the solubility product expression for each of the following slightly soluble ionic compounds:
(a) AgI, silver iodide, a solid with antiseptic properties
(b) CaCO3, calcium carbonate, the active ingredient in many over-the-counter chewable antacids
(c) Mg(OH)2, magnesium hydroxide, the active ingredient in Milk of Magnesia
(d) Mg(NH4)PO4, magnesium ammonium phosphate, an essentially insoluble substance used in tests for magnesium
(e) Ca5(PO4)3OH, the mineral apatite, a source of phosphate for fertilizers
(Hint: When determining how to break (d) and (e) up into ions, refer to the list of polyatomic ions in the section on chemical nomenclature.)
Solution
(a) AgI (s) ⇌ Ag+ (aq) + I– (aq)
Ksp = [Ag+][I–]
(b) CaCO3 (aq) ⇌ Ca2+ (aq) + CO32- (aq)
Ksp = [Ca2+][CO32-]
(c) Mg(OH)2 (s) ⇌ Mg2+ (aq) + 2OH– (aq)
Ksp = [Mg2+(aq)][OH–]2
(d) Mg(NH4)PO4 (s) ⇌ Mg+ (aq) + NH4+ (aq) + PO43- (aq)
Ksp = [Mg2+][NH4+][PO43-]
(e) Ca5(PO4)3OH (s) ⇌ 5Ca2+ (aq) + 3PO43- (aq) + OH– (aq)
Ksp = [Ca2+]5[PO43-]3[OH–]
Check Your Learning 6.4.1 – Writing Equations and Solubility Products
Write the ionic equation for the dissolution and the solubility product for each of the following slightly soluble compounds:
(a) BaSO4
(b) Ag2SO4
(c) Al(OH)3
(d) Pb(OH)Cl
Answer
(a) BaSO4 (s) ⇌ Ba2+ (aq) + SO42- (aq)
Ksp = [Ba2+][SO42-]
(b) Ag2SO4 (s) ⇌ 2Ag+ (aq) + SO42- (aq)
Ksp = [Ag+]2[SO42-]
(c) Al(OH)3 (s) ⇌ Al3+ (aq) + 3OH– (aq)
Ksp = [Al3+][OH–]3
(d) Pb(OH)Cl (s) ⇌ Pb2+ (aq) + OH– (aq)+ Cl– (aq)
Ksp = [Pb2+][OH–][Cl–]
Now we will extend the discussion of Ksp and show how the solubility product constant is determined from the solubility of its ions, as well as how Ksp can be used to determine the molar solubility of a substance.
The Ion Product
The ion product (Q) of a salt is the product of the concentrations of the ions in solution raised to the same powers as in the solubility product expression. It is analogous to the reaction quotient (Q) discussed for equilibria in Chapter 4. Whereas Ksp describes equilibrium concentrations, the ion product describes concentrations that are not necessarily equilibrium concentrations.
As summarized in Figure 6.4.2, there are three possible conditions for an aqueous solution of an ionic solid:
- Q < Ksp The solution is unsaturated, and more of the ionic solid, if available, will dissolve.
- Q = Ksp The solution is saturated and at equilibrium.
- Q > Ksp The solution is supersaturated, and ionic solid will precipitate.
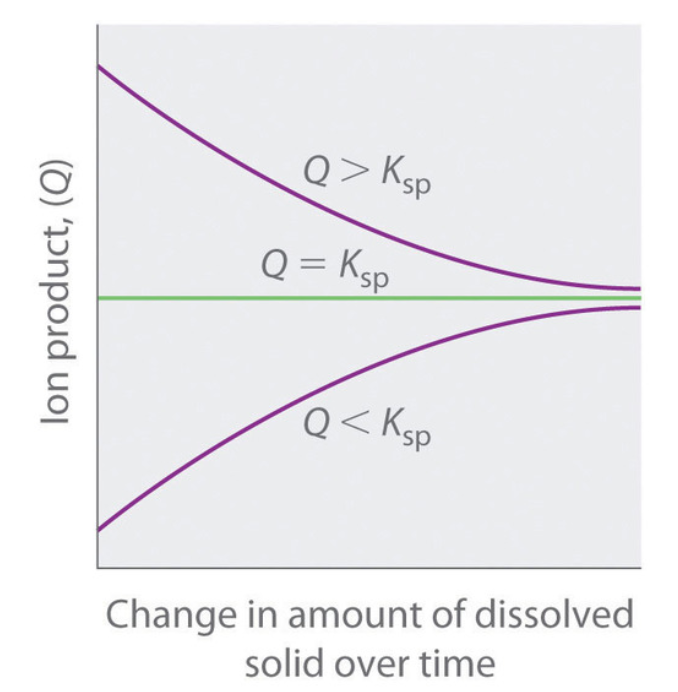
Figure 6.4.2. The relationship between Q and Ksp. If Q is less than Ksp, the solution is unsaturated and more solid will dissolve until the system reaches equilibrium (Q = Ksp). If Q is greater than Ksp, the solution is supersaturated and solid will precipitate until Q = Ksp. If Q = Ksp, the rate of dissolution is equal to the rate of precipitation; the solution is saturated, and no net change in the amount of dissolved solid will occur.
The process of calculating the value of the ion product and comparing it with the magnitude of the solubility product is a straightforward way to determine whether a solution is unsaturated, saturated, or supersaturated. More important, the ion product tells chemists whether a precipitate will form when solutions of two soluble salts are mixed.
Ksp and Solubility
Recall that the definition of solubility is the maximum possible concentration of a solute in a solution at a given temperature and pressure. We can determine the solubility product of a slightly soluble solid from that measure of its solubility at a given temperature and pressure, provided that the only significant reaction that occurs when the solid dissolves is its dissociation into solvated ions, that is, the only equilibrium involved is:
MpXq (s) ⇌ pMm+ (aq) + qXn– (aq)
Equation 6.4.1 – Dissolution of a slightly soluble solid.
In this case, we calculate the solubility product by taking the solid’s solubility expressed in units of moles per liter (mol/L), known as its molar solubility.
Example 6.4.3 – Calculation of Ksp from Equilibrium Concentrations
Fluorite, CaF2, is a slightly soluble solid that dissolves according to the equation:
CaF2 (s) ⇌ Ca2+ (aq) + 2F– (aq)
The concentration of Ca2+ in a saturated solution of CaF2 is 2.15 × 10–4 M; therefore, that of F– is 4.30 × 10–4 M, that is, twice the concentration of Ca2+. What is the solubility product of fluorite?
Solution
First, write out the Ksp expression, then substitute in concentrations and solve for Ksp:
CaF2 (s) ⇌ Ca2+ (aq) + 2F– (aq)
A saturated solution is a solution at equilibrium with the solid. Thus:
Ksp = [Ca2+][F–]2 = (2.1×10-4)(4.2×10-4)2 = 3.7×10-11
As with other equilibrium constants, we do not include units with Ksp.
Check Your Learning 6.4.2 – Calculation of Ksp from Equilibrium Concentrations
In a saturated solution that is in contact with solid Mg(OH)2, the concentration of Mg2+ is 1.31 × 10–4 M. What is the solubility product for Mg(OH)2?
Mg(OH)2 (s) ⇌ Mg2+ (aq) + 2OH– (aq)
Answer
Ksp = 8.99 × 10–12
Example 6.4.4 – Determination of Molar Solubility from Ksp
The Ksp of copper(I) bromide, CuBr, is 6.3 × 10–9. Calculate the molar solubility of copper bromide.
Solution
The solubility product constant of copper(I) bromide is 6.3 × 10–9.
The reaction is:
CuBr (s) ⇌ Cu+ (aq) + Br– (aq)
First, write out the solubility product equilibrium constant expression:
Ksp = [Cu+][Br–]
Create an ICE table (as introduced in Chapter 4), leaving the CuBr column empty as it is a solid (its activity is equal to one) and thus does not appear in the Ksp expression:
CuBr (s) ⇌ Cu+ (aq) + Br– (aq)
| CuBr (s) | Cu+ (aq) | Br– (aq) | |
| Initial (M) | / | 0 | 0 |
| Change (M) | / | +x | +x |
| Equilibrium (M) | / | x | x |
At equilibrium:
Ksp = [Cu+][Br–]
6.3×10-9 = (x)(x)=x2
x = sqrt(6.3×10-9) = 7.9×10-5
Therefore, the molar solubility of CuBr is 7.9 × 10–5 M.
Check Your Learning 6.4.3 – Determination of Molar Solubility from Ksp
The Ksp of AgI is 1.5 × 10–16. Calculate the molar solubility of silver iodide.
Answer
1.2 × 10–8 M
Example 6.4.5 – Determination of Molar Solubility from Ksp, Part II
The Ksp of calcium hydroxide, Ca(OH)2, is 1.3 × 10–6. Calculate the molar solubility of calcium hydroxide.
Solution
The solubility product constant of calcium hydroxide is 1.3 × 10–6.
The reaction is:
Ca(OH)2 (s) ⇌ Ca2+ (aq) + 2 OH– (aq)
First, write out the solubility product equilibrium constant expression:
Ksp = [Ca2+][OH–]2
Create an ICE table, leaving the Ca(OH)2 column empty as it is a solid and does not contribute to the Ksp:
Ca(OH)2 (s) ⇌ Ca2+ (aq) + 2OH– (aq)
| Ca(OH)2 (s) | Ca2+ (aq) | 2OH– (aq) | |
| Initial (M) | / | 0 | 0 |
| Change (M) | / | +x | +2x |
| Equilibrium (M) | / | x | 2x |
At equilibrium:
Ksp = [Ca2+][OH–]2
1.3×10-6 = (x)(2x)2 = (x)(4x2) = 4x3
x = cbrt(1.3×10-6/4) = 6.9×10-3
Therefore, the molar solubility of Ca(OH)2 is 1.3 × 10–2 M.
Check Your Learning 6.4.4 – Determination of Molar Solubility from Ksp, Part II
The Ksp of PbI2 is 1.4 × 10–8. Calculate the molar solubility of lead(II) iodide.
Answer
1.5 × 10–3 M
Note that solubility is not always given as a molar value. When the solubility of a compound is given in some unit other than moles per liter, we must convert the solubility into moles per liter (i.e., molarity) in order to use it in the solubility product constant expression. The following example shows how to perform those unit conversions before determining the solubility product equilibrium.
Example 6.4.6 – Determination of Ksp from Gram Solubility
Many of the pigments used by artists in oil-based paints (Figure 6.4.3) are sparingly soluble in water. For example, the solubility of the artist’s pigment chrome yellow, PbCrO4, is 4.6 × 10–6 g/L. Determine the solubility product equilibrium constant for PbCrO4.

Figure 6.4.3. Oil paints contain pigments that are very slightly soluble in water. In addition to chrome yellow (PbCrO4), examples include Prussian blue (Fe7(CN)18), the reddish-orange colour vermilion (HgS), and green colour veridian (Cr2O3). (credit: Sonny Abesamis)
Solution
We are given the solubility of PbCrO4 in grams per litre. If we convert this solubility into moles per litre, we can find the equilibrium concentrations of Pb2+ and CrO42−, then Ksp:

Use the molar mass of PbCrO4 (323.2g/mol) to convert the solubility of PbCrO4 in grams per litre into moles per litre:
[PbCrO4] = (4.6×10-6 g PbCrO4/ 1 L) × (1 mol PbCrO4 / 323.2 g PbCrO4)
= 1.4×10-8 mol PbCrO4 / 1 L
[PbCrO4] = 1.4×10-8 M
The chemical equation for the dissolution indicates that 1 mol of PbCrO4 gives 1 mol of Pb2+(aq) and 1 mol of CrO42−(aq):
PbCrO4 (s) ⇌ Pb2+ (aq) + CrO42- (aq)
Thus, at equilibrium, both [Pb2+] and [CrO42−] are equal to the molar solubility of PbCrO4:
[Pb2+(aq)] = [CrO42-(aq)] = 1.4×10-8 M
Solve.
Ksp = [Pb2+][CrO42−] = (1.4 × 10–8)(1.4 × 10–8) = 2.0 × 10–16
Check Your Learning 6.4.5 – Determination of Ksp from Gram Solubility
The solubility of thallium(I) chloride (TlCl), an intermediate formed when thallium is being isolated from ores, is 3.46 grams per litre at 20°C. What is its solubility product?
Answer
1.7 × 10–4
Example 6.4.7 – Calculating the Solubility of Hg2Cl2
Calomel, Hg2Cl2, is a compound composed of the diatomic ion of mercury(I), Hg22+, and chloride ions, Cl–. Although most mercury compounds are now known to be poisonous, eighteenth-century physicians used calomel as a medication. Their patients rarely suffered any mercury poisoning from the treatments because calomel is quite insoluble:
Hg2Cl2 (s) ⇌ Hg22+ (aq) + 2Cl– (aq)
Calculate the molar solubility of Hg2Cl2.
Solution
The molar solubility of Hg2Cl2 is equal to the concentration of Hg22+ ions because for each 1 mol of Hg2Cl2 that dissolves, 1 mol of Hg22+ forms:

Determine the direction of change. Before any Hg2Cl2 dissolves, Q is zero, and the reaction will shift to the right to reach equilibrium.
Determine x and equilibrium concentrations. Concentrations and changes are given in the following ICE table:
Hg2Cl2 (s) ⇌ Hg22+(aq) + 2Cl– (aq)
| Hg2Cl2 (s) | Hg22+(aq) | 2Cl– (aq) | |
| Initial (M) | / | 0 | 0 |
| Change (M) | / | +x | +2x |
| Equilibrium (M) | / | x | 2x |
Note that the change in the concentration of Cl– (2x) is twice as large as the change in the concentration of Hg22+ (x) because 2 mol of Cl– forms for each 1 mol of Hg22+ that forms. Hg2Cl2 is a pure solid, so it does not appear in the calculation.
Solve for x and the equilibrium concentrations. We substitute the equilibrium concentrations into the expression for Ksp and calculate the value of x:
Ksp = [Hg22+][Cl–]2
1.1×10-18 =(x)(2x)2
4x3=1.1×10-18
x = cbrt(1.1×10-18/4) = 6.5×10-7 M
[Hg22+] = 6.5×10-7 M = 6.5×10-7 M
[Cl–] = 2x = 2(6.5×10-7 M) = 1.3×10-6 M
The molar solubility of Hg2Cl2 is equal to [Hg22+], or 6.5 × 10–7 M.
Check the work. At equilibrium, Q = Ksp:
Q = [Hg22+][Cl–]2 = (6.5×10-7)(1.3×10-6)2 = 1.1×10-18
The calculations check out.
Check Your Learning 6.4.6 – Calculating the Solubility of Hg2Cl2
Determine the molar solubility of MgF2 from its solubility product: Ksp = 6.4 × 10–9.
Answer
1.2 × 10–3 M
Tabulated Ksp values can also be compared to reaction quotients calculated from experimental data to tell whether a solid will precipitate in a reaction under specific conditions: Q equals Ksp at equilibrium; if Q is less than Ksp, the solid will dissolve until Q equals Ksp; if Q is greater than Ksp, precipitation will occur at a given temperature until Q equals Ksp.
|
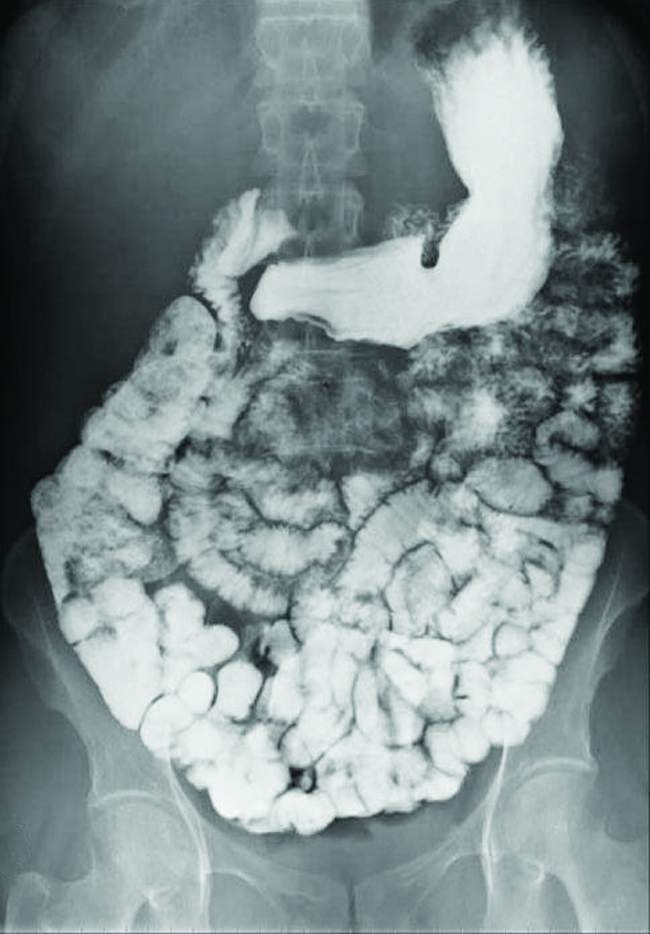
Using Barium Sulfate for Medical Imaging Various types of medical imaging techniques are used to aid diagnosis of illnesses in a noninvasive manner. One such technique utilizes the ingestion of a barium compound before taking an X-ray image. A suspension of barium sulfate, a chalky powder, is ingested by the patient. Since the Ksp of barium sulfate is 1.1 × 10–10, very little of it dissolves as it coats the lining of the patient’s intestinal tract. Barium-coated areas of the digestive tract then appear on an X-ray as white, allowing for greater visual detail than a traditional X-ray (Figure 6.4.4).
Figure 6.4.4. The suspension of barium sulfate coats the intestinal tract, which allows for greater visual detail than a traditional X-ray. (credit modification of work by “glitzy queen00”/Wikimedia Commons) Further diagnostic testing can be done using barium sulfate and fluoroscopy. In fluoroscopy, a continuous X-ray is passed through the body so the doctor can monitor, on a TV or computer screen, the barium sulfate’s movement as it passes through the digestive tract. Medical imaging using barium sulfate can be used to diagnose acid reflux disease, Crohn’s disease, and ulcers in addition to other conditions. You can visit this website for more information on how barium is used in medical diagnoses and which conditions it is used to diagnose. |
The Common Ion Effect and Solubility
What happens if we try to dissolve a sparingly soluble salt in an aqueous solution that already contains one of the salt’s ions? Following Section 6.1, this would be an example of the common ion effect. According to Le Chatelier’s Principle, the presence of product ion shifts the equilibrium towards the solid reactant, and we expect the solubility of the salt to be reduced.
Example 6.4.8 – The Common Ion Effect and Solubility
If we attempt to dissolve lead(II) chloride in a 0.100 M sodium chloride solution instead of in water, what is the equilibrium concentration of the lead(II) ions, as compared to pure water?
First, let us determine the solubility of PbCl2 in pure water. We can define x to be the concentration of the lead(II) ions at equilibrium, and use an ICE table:
PbCl2 (s) ⇌ Pb2+(aq) + 2Cl–(aq)
| PbCl2 (s) | Pb2+(aq) | 2Cl–(aq) | |
| Initial (M) | / | 0 | 0 |
| Change (M) | / | +x | +2x |
| Equilibrium (M) | / | x | 2x |
We substitute the equilibrium concentrations into the expression for Ksp and calculate the value of x:
Ksp = [Pb2+][Cl–]2
1.7×10-5 = (x)(2x)2
4x3 = 1.7×10-5
x = cbrt(1.7×10-5/4) = 0.016 M
Now, to find the solubility of lead (II) chloride in 0.100 M NaCl, we repeat this process, only we take into account the presence of the common ion. In this example, the common ion is the chloride ion. Since NaCl is a soluble salt, we assume 100% ionization and thus [Cl–]i = 0.100 M.
PbCl2 (s) ⇌ Pb2+(aq) + 2Cl–(aq)
| PbCl2 (s) | Pb2+(aq) | 2Cl–(aq) | |
| Initial (M) | / | 0 | 0.100 |
| Change (M) | / | +x | +2x |
| Equilibrium (M) | / | x | 0.100+2x |
Again, we substitute the equilibrium concentrations into the expression for Ksp and calculate the value of x, and to simplify the calculation, we assume that the value of x is small:
Ksp = [Pb2+][Cl–]2
1.7×10-5 = (x)(0.100+2x)2
1.7×10-5 = (x)(0.100)2
x = 1.7×10-3 M
Finally, let’s compare the obtained values:
Original solution:
[Pb2+] = 0.016 M
In 0.100 M NaCl solution:
[Pb2+] = 0.0017 M
The concentration of the lead(II) ions has decreased by a factor of about 10, confirming that the common ion effect inhibits the solubility of a sparingly soluble salt. If more concentrated solutions of sodium chloride are used, the solubility decreases further.
Check Your Learning 6.4.7 – The Common Ion Effect and Solubility
BaSO4 is a sparingly soluble salt that ionizes into Ba2+ and SO42-:
BaSO4 (s) ⇌ Ba2+(aq) + SO42-(aq)
Ksp = 1.1×10-10
Find the concentration of each ion at equilibrium for a saturated solution of barium sulfate. Next, lithium sulfate (Li2SO4) is added to the reaction vessel until its concentration is 0.500 M. What is the concentration of barium and sulfate ions after the addition of lithium sulfate?
Answer
Before addition of Li2SO4:
[Ba2+] = 1.0 x 10-5 M , [SO42-] = 1.0 x 10-5 M
After addition of Li2SO4:
[Ba2+] = 2.2 x 10-10 M , [SO42-] = 0.500 M
Check Your Learning 6.4.8 – The Common Ion Effect and Solubility
Calculate the solubility of silver carbonate in a 0.25 M solution of sodium carbonate. The Ksp of silver carbonate is 8.46 × 10−12 at 25°C.
Answer
2.9 × 10−6 M (versus 1.3 × 10−4 M in pure water)
Effect of pH on solubility
For certain salts, hydronium and hydroxide ion concentrations can influence solubility, as a special case of the common ion effect. Taking the concept of hydrolysis, introduced in Chapter 5, and applying Le Chatelier’s Principle to sparingly soluble salts, we can qualitatively predict that:
- ACIDIC salts will be less soluble in acid (pH < 7), and more soluble in base (pH > 7).
- BASIC salts will be less soluble in base (pH > 7), and more soluble in acid (pH < 7).
- NEUTRAL salts have solubilities unaffected by pH.
Consider the example of cobalt (II) hydroxide. It dissolves in the following equilibrium:
Co(OH)2 (s) ⇋ Co2+ (aq) + 2 OH– (aq)
Ksp = 2.5 x 10-16 = [Co2+][OH–]2
We can compare the solubility of this compound in pure water (where [OH–] = 1.0 x 10–7) versus its solubility in a pH = 6 buffer solution (where [OH–] = 1.0 x 10–8), using the following two ICE tables:
|
Pure water, [OH–] = 1 x 10-7 M |
Buffer (pH = 6), [OH–] = 1 x 10-8 M |
||||||
|
Co(OH)2 (s) ⇋ Co2+ (aq) + 2 OH– (aq) |
Co(OH)2 (s) ⇋ Co2+ (aq) + 2 OH– (aq) | ||||||
|
I |
– |
0 |
1 x 10-7 |
I |
– |
0 |
1 x 10-8 |
|
C |
– |
+x |
+2x |
C |
– |
+x |
NO change |
|
E |
– |
x |
1 x 10-7 +2x |
E |
– |
x |
1 x 10-8 |
|
Ksp = (x)(1.0 x 10-7 + 2x)2 s ≈ (x)(2x)2 s = 1.1 x 10-5 M |
Ksp = (x)(1.0 x 10-8)2 s = (Ksp)/(1.0 x 10-8)2 s > 50 M (soluble!) |
||||||
From the above calculations, we see that Co(OH)2, originally only slightly soluble in neutral water, becomes much more soluble under acidic conditions. Why is this so? Complete the exercise below to illustrate the reason.
Check Your Learning 6.4.9 – The Common Ion Effect and Solubility
The equilibrium for the dissolution of cobalt (II) hydroxide is:
Co(OH)2 (s) ⇋ Co2+ (aq) + 2 OH– (aq) Ksp = 5.9 x 10–15
In acidic solution, each hydroxide ion produced is neutralized by a hydronium ion. As we saw in Chapter 5, the net ionic equation for the acid-base neutralization is the inverse of the autoionization of water:
OH– (aq) + H3O+ (aq) ⇋ 2H2O(l) K = 1/Kw = 1.0 x 1014
Combine the two equilibria provided, taking note of stoichiometry, to find an overall chemical equation for the dissolution of cobalt (II) hydroxide in acidic solution, as well as the value of the equilibrium constant. (Recall the rules for manipulating equilibrium constants from Chapter 4).
Answer:
Co(OH)2 (s) + 2H3O+ (aq) ⇋ Co2+ (aq) + 4H2O (l), K = 5.9 x 1013
Predicting Precipitation
The equation that describes the equilibrium between solid calcium carbonate and its solvated ions is:
CaCO3 (s) ⇌ Ca2+ (aq) + CO32- (aq)
We can establish this equilibrium either by adding solid calcium carbonate to water or by mixing a solution that contains calcium ions with a solution that contains carbonate ions. If we add calcium carbonate to water, the solid will dissolve until the concentrations are such that the value of the reaction quotient (Q = [Ca2+][CO32−]) is equal to the solubility product (Ksp = 8.7 × 10–9). If we mix a solution of calcium nitrate, which contains Ca2+ ions, with a solution of sodium carbonate, which contains CO32− ions, the slightly soluble ionic solid CaCO3 will precipitate, provided that the concentrations of Ca2+ and CO32− ions are such that Q is greater than Ksp for the mixture. The reaction shifts to the left and the concentrations of the ions are reduced by formation of the solid until the value of Q equals Ksp. A saturated solution in equilibrium with the undissolved solid will result. If the concentrations are such that Q is less than Ksp, then the solution is not saturated and no precipitate will form.
We can compare numerical values of Q with Ksp to predict whether precipitation will occur, as the following example shows. (Note: Since all forms of equilibrium constants are temperature dependent, we will assume a room temperature environment going forward in this chapter unless a different temperature value is explicitly specified.)
Example 6.4.9 – Precipitation of Mg(OH)2
The first step in the preparation of magnesium metal is the precipitation of Mg(OH)2 from sea water by the addition of lime, Ca(OH)2, a readily available inexpensive source of OH– ion:
Mg(OH)2 (s) ⇌ Mg2+ (aq) + 2OH– (aq)
The concentration of Mg2+(aq) in sea water is 0.0537 M. Will Mg(OH)2 precipitate when enough Ca(OH)2 is added to give a [OH–] of 0.0010 M?
Solution
This problem asks whether the reaction:
Mg(OH)2 (s) ⇌ Mg2+ (aq) + 2OH– (aq)
shifts to the left and forms solid Mg(OH)2 when [Mg2+] = 0.0537 M and [OH–] = 0.0010 M. The reaction shifts to the left if Q is greater than Ksp. Calculation of the reaction quotient under these conditions is shown here:
Q = [Mg2+][OH–]2 = (0.0537)(0.0010)2 = 5.4 x 10-8
Because Q is greater than Ksp (Q = 5.4 × 10-8 is larger than Ksp = 8.9 × 10-12), we can expect the reaction to shift to the left and form solid magnesium hydroxide. Mg(OH)2 (s) forms until the concentrations of magnesium ion and hydroxide ion are reduced sufficiently so that the value of Q is equal to Ksp.
Check Your Learning 6.4.10 – Precipitation of Mg(OH)2
Will KClO4 precipitate when 20 mL of a 0.050 M solution of K+ is added to 80 mL of a 0.50 M solution of ClO4−? (Remember to calculate the new concentration of each ion after mixing the solutions before plugging into the reaction quotient expression.)
Answer
No, Q = 4.0 × 10–3, which is less than Ksp = 1.05 × 10–2
In the previous example, we have seen that a precipitate forms when Q is greater than Ksp. In general, according to Equation 6.4.1, when a solution of a soluble salt of the Mm+ ion is mixed with a solution of a soluble salt of the Xn– ion, the solid, MpXq precipitates if the value of Q for the mixture of Mm+ and Xn– is greater than Ksp for MpXq. Thus, if we know the concentration of one of the ions of a slightly soluble ionic solid and the value for the solubility product of the solid, then we can calculate the concentration that the other ion must exceed for precipitation to begin. To simplify the calculation, we will assume that precipitation begins when the reaction quotient becomes equal to the solubility product constant.
Example 6.4.10 – Precipitation of Calcium Oxalate
Blood will not clot if calcium ions are removed from its plasma. Some blood collection tubes contain salts of the oxalate ion, C2O42−, for this purpose (Figure 6.4.5). At sufficiently high concentrations, the calcium and oxalate ions form solid calcium oxalate monohydrate, CaC2O4•H2O. The concentration of Ca2+ in a sample of blood serum is 2.2 × 10–3 M. What concentration of C2O42− ion must be established before CaC2O4•H2O begins to precipitate?
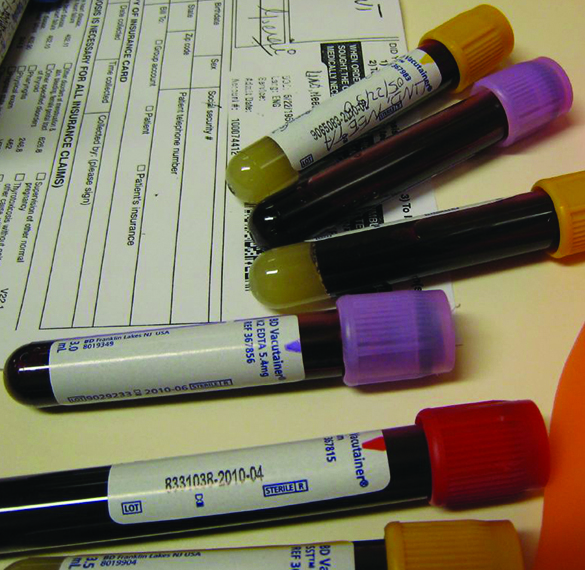
Figure 6.4.5. Anticoagulants can be added to blood that will combine with the Ca2+ ions in blood serum and prevent the blood from clotting. (credit: modification of work by Neeta Lind)
Solution
The equilibrium expression is:
CaC2O4 (s) ⇌ Ca2+ (aq) + C2O42- (aq)
For this reaction:
Ksp = [Ca2+][C2O42-] = 1.96×10-8 (see Appendix L)
Solid CaC2O4 does not begin to form until Q equals Ksp. Because we know Ksp and [Ca2+], we can solve for the concentration of C2O42− that is necessary to produce the first trace of solid precipitate:
Q = Ksp = [Ca2+(aq)][C2O42-(aq)] = 1.96×10-8
(2.2×10-3)[C2O42-(aq)] = 1.96×10-8
[C2O42-(aq)] = 1.96×10-8/2.2×10-3 = 8.9×10-6 M
A concentration of [C2O42−] = 8.9 × 10–6 M is necessary to initiate the precipitation of CaC2O4 under these conditions.
Check Your Learning 6.4.11 – Precipitation of Calcium Oxalate
If a solution contains 0.0020 mol of CrO42− per litre, what concentration of Ag+ ion must be reached by adding solid AgNO3 before Ag2CrO4 begins to precipitate? Neglect any increase in volume upon adding the solid silver nitrate.
Answer
4.5 × 10–9 M
It is sometimes useful to know the concentration of an ion that remains in solution after precipitation. We can use the solubility product for this calculation too: If we know the value of Ksp and the concentration of one ion in solution, we can calculate the concentration of the second ion remaining in solution. The calculation is of the same type as that in the previous example—calculation of the concentration of a species in an equilibrium mixture from the concentrations of the other species and the equilibrium constant. However, the concentrations are different; we are calculating concentrations after precipitation is complete, rather than at the start of precipitation.
Example 6.4.11 – Concentrations Following Precipitation
Clothing washed in water that has an aqueous manganese (II) ion (Mn2+) concentration exceeding 0.1 mg/L (1.8 × 10–6 M) may be stained by the manganese upon oxidation, but the amount of Mn2+ in the water can be reduced by adding a base. If a person doing laundry wishes to add a buffer to keep the pH high enough to precipitate the manganese as the hydroxide, Mn(OH)2, what pH is required to keep [Mn2+] equal to 1.8 × 10–6 M?
Solution
The dissolution of Mn(OH)2 is described by the equation:
Mn(OH)2 (s) ⇌ Mn2+ (aq) + 2OH– (aq)
We need to calculate the concentration of OH– when the concentration of Mn2+ is 1.8 × 10–6 M. From that, we calculate the pH. At equilibrium:
Ksp = [Mn2+][OH–]2
Or:
(1.8×10-6)[OH–]2 = 2×10-3
So:
[OH–] = 3.3×10-4 M
Now we calculate the pH from the pOH:
pOH = -log[OH–] = -log(3.3×10-4) = 3.48
pH = 14.00-pOH = 14.00-3.80 = 10.52
If the person doing laundry adds a base, such as the sodium silicate (Na4SiO4) in some detergents, to the wash water until the pH is raised to 10.52, the manganese ion will be reduced to a concentration of 1.8 × 10–6 M; at that concentration or less, the ion will not stain clothing.
Check Your Learning 6.4.12 – Concentrations Following Precipitation
The first step in the preparation of magnesium metal is the precipitation of Mg(OH)2 from sea water by the addition of Ca(OH)2. The concentration of Mg2+(aq) in sea water is 5.37 × 10–2 M. Calculate the pH at which [Mg2+] is diminished to 1.0 × 10–5 M by the addition of Ca(OH)2.
Answer
pH = 10.97
When two anions form slightly soluble compounds with the same cation, or when two cations form slightly soluble compounds with the same anion, the less soluble compound (the compound with the smaller molar solubility) generally precipitates first when we add a precipitating agent to a solution containing both anions (or both cations). When the molar solubilities of the two compounds differ by two orders of magnitude or more (e.g., 10–2 vs. 10–4), almost all of the less soluble compound precipitates before any of the more soluble one does. This is an example of selective precipitation, where a reagent is added to a solution of dissolved ions causing one of the ions to precipitate out before the rest.
|
The Role of Precipitation in Wastewater Treatment Solubility equilibria are useful tools in the treatment of wastewater carried out in facilities that may treat the municipal water in your city or town (Figure 6.4.6). Specifically, selective precipitation is used to remove contaminants from wastewater before it is released back into natural bodies of water. For example, phosphate ions (PO42−) are often present in the water discharged from manufacturing facilities. An abundance of phosphate causes excess algae to grow, which impacts the amount of oxygen available for marine life as well as making water unsuitable for human consumption.
Figure 6.4.6. Wastewater treatment facilities, such as this one, remove contaminants from wastewater before the water is released back into the natural environment. (credit: “eutrophication&hypoxia”/Wikimedia Commons) One common way to remove phosphates from water is by the addition of calcium hydroxide, known as lime, Ca(OH)2. The lime is converted into calcium carbonate, a strong base, in the water. As the water is made more basic, the calcium ions react with phosphate ions to produce hydroxyapatite, Ca5(PO4)3(OH), which then precipitates out of the solution: 10Ca2+(aq) + 6PO43-(aq) + 2OH–(aq) ⇌ Ca10(PO4)6⋅(OH)2(s) The precipitate is then removed by filtration and the water is brought back to a neutral pH by the addition of CO2 in a recarbonation process. Other chemicals can also be used for the removal of phosphates by precipitation, including iron(III) chloride and aluminum sulfate. View this site for more information on how phosphorus is removed from wastewater. |
Selective precipitation can also be used in qualitative analysis. In this method, reagents are added to an unknown chemical mixture in order to induce precipitation. Certain reagents cause specific ions to precipitate out; therefore, the addition of the reagent can be used to determine whether the ion is present in the solution.
View this simulation to study the process of salts dissolving and forming saturated solutions and precipitates for specific compounds, or compounds for which you select the charges on the ions and the Ksp.
Example 6.4.12 – Precipitation of Silver Halides
A solution contains 0.0010 mol of KI and 0.10 mol of KCl per liter. AgNO3 is gradually added to this solution. Which forms first, solid AgI or solid AgCl?
Solution
The two equilibria involved are:
AgCl (s) ⇌ Ag+ (aq) + Cl– (aq), Ksp = 1.6×10-10
AgI (s) ⇌ Ag+ (aq) + I– (aq), Ksp = 1.5×10-16
In this example, both salts form the same number of ions (1 mol of dissolved solid produces 1 mol of cations and 1 mol of anions) and so in both cases, the Ksp value is calculated as the square of the molar solubility (i.e. if the molar solubility is x, Ksp = x2). Consequently, we can compare these Ksp values directly to get a qualitative sense of the order of precipitation. Note that Ksp values may NOT be directly compared if the number of ions formed in the dissolution equilibrium is not identical (for example, it would not be appropriate to compare the Ksp value of AgCl to that of Ag2SO4).
Fortunately, in this case, since the Ksp values identically correlate to each solid’s molar solubility (Ksp = x2), that means we can deduce that if the solution contained about equal concentrations of Cl– and I–, then the silver salt with the smallest Ksp (AgI) would precipitate first. The concentrations are not equal, however, so we should find the [Ag+] at which AgCl begins to precipitate and the [Ag+] at which AgI begins to precipitate. The salt that forms at the lower [Ag+] precipitates first.
For AgI: AgI precipitates when Q equals Ksp for AgI (1.5 × 10–16). When [I–] =
0.0010 M:
Q = [Ag+][I–] = [Ag+](0.0010) = 1.5×10-16
[Ag+] = (1.8×10-10)(0.10) = 1.6×10-9 M
AgI begins to precipitate when [Ag+] is 1.5 × 10–13 M.
For AgCl: AgCl precipitates when Q equals Ksp for AgCl (1.6 × 10–10). When [Cl–] = 0.10 M:
Q =[Ag+][Cl–] = [Ag+](0.10) = 1.6×10-10
[Ag+] = 1.8×10-10(0.10) = 1.6×10-9 M
AgCl begins to precipitate when [Ag+] is 1.6 × 10–9 M.
AgI begins to precipitate at a lower [Ag+] than AgCl, so AgI begins to
precipitate first.
Check Your Learning 6.4.13 – Precipitation of Silver Halides
If silver nitrate solution is added to a solution which is 0.050 M in both Cl– and Br– ions, at what [Ag+] would precipitation begin, and what would be the formula of the precipitate?
Answer
[Ag+] = 1.0 × 10–11 M; AgBr precipitates first
Questions
★ Questions
1. Write the ionic equation for the dissolution and the Ksp expression for each of the following slightly soluble ionic compounds:
(a) LaF3
(b) CaCO3
(c) Ag2SO4
(d) Pb(OH)2
2. The Handbook of Chemistry and Physics gives solubilities of the following compounds in grams per 100 mL of water. Because these compounds are only slightly soluble, assume that the volume does not change on dissolution and calculate the solubility product for each.
(a) BaSeO4, 0.0118 g/100 mL
(b) Ba(BrO3)2·H2O, 0.30 g/100 mL
(c) NH4MgAsO4·6H2O, 0.038 g/100 mL
(d) La2(MoO4)3, 0.00179 g/100 mL
3. Use solubility products and predict which of the following salts is the most soluble, in terms of moles per liter, in pure water: CaF2, Hg2Cl2, PbI2, or Sn(OH)2.
4. Assuming that no equilibria other than dissolution are involved, calculate the molar solubility of each of the following from its solubility product:
(a) KHC4H4O6
(b) PbI2
(c) Ag4[Fe(CN)6], a salt containing the Fe(CN)4− ion
(d) Hg2I2
★★ Questions
5. Assuming that no equilibria other than dissolution are involved, calculate the concentration of all solute species in each of the following solutions of salts in contact with a solution containing a common ion. Show that changes in the initial concentrations of the common ions can be neglected.
(a) AgCl(s) in 0.025 M NaCl
(b) CaF2(s) in 0.00133 M KF
(c) Ag2SO4(s) in 0.500 L of a solution containing 19.50 g of K2SO4
(d) Zn(OH)2(s) in a solution buffered at a pH of 11.45
6. Most barium compounds are very poisonous; however, barium sulfate is often administered internally as an aid in the X-ray examination of the lower intestinal tract (Figure 6.4.4). This use of BaSO4 is possible because of its low solubility. Calculate the molar solubility of BaSO4 and the mass of barium present in 1.00 L of water saturated with BaSO4.
7. The solubility product of CaSO4·2H2O is 2.4 × 10–5. What mass of this salt will dissolve in 1.0 L of 0.010 M SO42−?
8. Which of the following carbonates will form first? Which of the following will form last? Explain.
(a) MgCO3 Ksp = 3.5 × 10−8
(b) CaCO3 Ksp = 4.2 × 10−7
(c) SrCO3 Ksp = 3.9 × 10−9
(d) BaCO3 Ksp = 4.4 × 10−5
(e) MnCO3 Ksp = 5.1 × 10−9
9. How many grams of Milk of Magnesia, Mg(OH)2 (s) (58.3 g/mol), would be soluble in 200 mL of water. Ksp = 7.1 × 10–12. Include the ionic reaction and the expression for Ksp in your answer. (Kw = 1 × 10–14 = [H3O+][OH–])
10. A volume of 0.800 L of a 2 × 10–4 M Ba(NO3)2 solution is added to 0.200 L of 5 × 10–4 M Li2SO4. Does BaSO4 precipitate? Explain your answer.
11. Calculate the concentration of PO43− when Ag3PO4 starts to precipitate from a solution that is 0.0125 M in Ag+.
Answers
1. (a) LaF3 (s) ⇌ La3+ (aq) + 3F– (aq) Ksp = [La3+][F–]3
(b) CaCO3 (s) ⇌ Ca3+ (aq) + CO32- (aq) Ksp =[Ca2+][CO32-]
(c) Ag2SO4 (s) ⇌ 2Ag+ (aq) + SO42- (aq) Ksp = [Ag+]2[SO42-]
(d) Pb(OH)2 (s) ⇌ Pb2+ (aq) + 2OH– (aq) Ksp = [Pb2+][OH–]2
2. (a) 1.77 × 10–7; (b) 1.6 × 10–6; (c) 2.2 × 10–9; (d) 7.91 × 10–22
3. PbI2 is the most soluble.
4. (a) 2 × 10–2 M; (b) 1.5 × 10–3 M; (c) 2.27 × 10–9 M; (d) 2.2 × 10–10 M
5. (a) 6.4×10-9 M = [Ag+], [Cl-] = 0.025 M
6. The molar solubility of BaSO4 is 1.51 × 10–4 M and the mass of barium present in 1 L of water in 0.020 g.
7. Mass (CaSO4·2H2O) = 0.72 g/L
8. MnCO3 will form first, since it has the smallest Ksp value it is the least soluble. MnCO3 will be the last to precipitate, it has the largest Ksp value.
10. No precipitation occurs because the value of the solubility product (2.3 x 10-8) is greater than the ionic product (1.6 x 10-8).
11. 9.2 × 10−13 M
Extent to which a solute may be dissolved in water, or any solvent
Of concentration equal to solubility; containing the maximum concentration of solute possible for a given temperature and pressure
Of concentration that exceeds solubility (more than the normal maximum amount of solute in it); a nonequilibrium state
Insoluble product that forms from reaction of soluble reactants
Equilibrium constant for the dissolution of an ionic compound
Product of the concentrations of the ions in solution raised to the same powers as in the solubility product expression; analogous to the reaction quotient (Q) discussed for gaseous equilibria
Solubility of a compound expressed in units of moles per liter (mol/L)
Process in which ions are separated using differences in their solubility with a given precipitating reagent