6.2 – Buffer Solutions

A mixture of a weak acid and its conjugate base (or a mixture of a weak base and its conjugate acid) is called a buffer solution, or simply a buffer. Buffer solutions resist a change in pH when small amounts of a strong acid or a strong base are added (Figure 6.2.1). A solution of acetic acid and sodium acetate (CH₃COOH + CH₃COONa) is an example of a buffer that consists of a weak acid and its conjugate base, whereas a solution of ammonia and ammonium chloride (NH₃ + NH₄Cl) is an example of a buffer that consists of a weak base and its conjugate acid.

Figure 6.2.1. (a) The unbuffered solution on the left and the buffered solution on the right have the same pH (pH 8); they are basic, showing the yellow colour of the indicator methyl orange at this pH. (b) After the addition of 1 mL of a 0.01 M HCl solution, the buffered solution has not detectably changed its pH but the unbuffered solution has become acidic, as indicated by the change in colour of the methyl orange, which turns red at a pH of about 4. (credit: modification of work by Mark Ott)

How Buffers Work

Buffers are made from mixing a weak acid with its conjugate base or a weak base with its conjugate acid. It is vital that the acid and base form a conjugate pair; this way, the two species cannot neutralize one another. For example, if a buffer is formed from a weak acid HA and its conjugate base A^–, any proton transfer that occurs yields products that are identical to the reactants, a process known as an identity reaction:

HA + A^– → A^– + HA

Instead, the acid and base conjugate pair function to neutralize external sources of base and acid, respectively, in the following reactions:

HA + OH^– → A^– + H₂O

A^– + H₃O^– → HA + H₂O

We will return to these neutralization reactions later, but first let us examine the differences between acidic and basic buffers.

Acidic Buffers: Aqueous Mixtures of HA + A^–

If we mix together acetic acid and sodium acetate in water, the resulting aqueous solution has a pH < 7. It is acidic because the K_a of acetic acid (1.8 x 10^–5) is greater than the K_b of the conjugate base acetate (5.6 x 10^–10):

CH₃COOH + H₂O ⇌ CH₃COO^– + H₃O⁺ K_a = 1.8 x 10^–5

CH₃COO^– + H₂O ⇌ CH₃COOH + OH^–  K_b = 5.6 x 10^–10

Comparing the K values, the first equilibrium lies further towards products than the second, thus there is more hydronium ion than hydroxide ion in the mixture, producing an overall pH for the mixture that is acidic.

This solution is a buffer because it contains the conjugate pair of a weak acid and its conjugate base, HA and A^–, and both species are present in significant concentrations. This acts to keep the hydronium ion concentration (the pH) almost constant even after the addition of a strong acid or a strong base. The conjugate acid/base pair is able to neutralize the strong acid or base added to the solution.

For example, if an external source of acid increases the amount of H₃O⁺, the buffer counteracts this addition:

CH₃COO^– (aq) + H₃O⁺ (aq) → CH₃COOH (aq) + H₂O (l)

In this reaction, the conjugate base, CH₃COO^–, will neutralize the added acid, H₃O⁺. This reaction goes to completion, because the reaction of CH₃COO^– with H₃O⁺ has an equilibrium constant that is the inverse of the K_a for CH₃COOH: 1/K_a = 1/(1.8 x 10^-5) = 5.5 x 10⁴, indicating a heavily product-favoured reaction. So long as there is significantly more CH₃COO^– than H₃O⁺, the externally added H₃O⁺ will be consumed, increasing the concentration of CH₃COOH and decreasing the concentration of CH₃COO^– . But, since these two species are both present in large concentrations, the ratio of acid-to-conjugate base is nearly constant and there will be hardly any change in the amount of H₃O⁺ present once equilibrium is re-established.

If a strong base were added such as sodium hydroxide (NaOH):

CH₃COOH + OH^– (aq) + OH^– (aq) ⇌ CH₃COO^– (aq) + H₂O (l)

In this reaction, the conjugate acid, CH₃COOH, will neutralize added amounts of base, OH^–, slightly increasing the concentration of CH₃COO^– in the solution and decreasing the amount of CH₃COOH. Again, since most of the OH^– is neutralized, little pH change will occur.

Basic Buffers: aqueous mixtures of B + HB⁺

A mixture of ammonia and ammonium chloride is basic because the K_b for ammonia is greater than the K_a for the ammonium ion. It is a buffer because it also contains the conjugate acid of the weak base. If we add a base (hydroxide ions), ammonium ions in the buffer react with the hydroxide ions to form ammonia and water and reduce the hydroxide ion concentration almost to its original value:

NH₄⁺ (aq) + OH^– (aq) → NH₃ (aq) + H₂O (l)

If we add an acid (hydronium ions), ammonia molecules in the buffer mixture react with the hydronium ions to form ammonium ions and reduce the hydronium ion concentration almost to its original value:

H₃O⁺ (aq) + NH₃ (aq) → NH₄⁺ (aq) + H₂O (l)

The three parts of the following example illustrate the change in pH that accompanies the addition of base to a buffered solution of a weak acid and to an unbuffered solution of a strong acid.

Example 6.2.1 – pH Changes in Buffered and Unbuffered Solutions

Acetate buffers are used in biochemical studies of enzymes and other chemical components of cells to prevent pH changes that might change the biochemical activity of these compounds.

(a) Calculate the pH of an acetate buffer that is a mixture of 0.10 M acetic acid and 0.10 M sodium acetate.

(b) Calculate the pH after 1.0 mL of 0.10 M NaOH is added to 100 mL of this buffer, giving a solution with a total volume of 101 mL.

(c) Calculate the pH after 1.0 mL of 0.10 M NaOH is added to an 100 mL of an unbuffered solution of 1.8 × 10⁻⁵ M HCl.

Solution

(a) To determine the pH of the buffer solution we use a typical equilibrium calculation (as illustrated in earlier Examples):

Determine the direction of change. The equilibrium in a mixture of H₃O⁺, CH₃CO₂⁻, and CH₃CO₂H is:

CH₃CO₂H (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + CH₃CO₂^– (aq)

The equilibrium constant for CH₃CO₂H is not given, so we look it up in Appendix H: K_a = 1.8 × 10⁻⁵. With [CH₃CO₂H]_i = [CH₃CO₂⁻]_i= 0.10 M and [H₃O⁺]_i = ~0 M, the reaction shifts to the right to form H₃O⁺.

Determine x and equilibrium concentrations. A table of changes and concentrations follows:

CH₃CO₂H + H₂O ⇌ H₃O⁺ + CH₃CO₂^–

Solve for x and the equilibrium concentrations. We find:

x = 1.8×10^-5 M

and

[H₃O⁺] = 0+x = 1.8×10^-5 M

Thus:

Check the work. If we calculate all calculated equilibrium concentrations, we find that the equilibrium value of the reaction coefficient, Q = K_a.

Note: Notice that when [HA] = [A-], pH = pK_a. Qualitatively, one would expect a decrease in pH as the [HA] increases since this increases the [H₃O⁺]. Inversely, one would expect an increase in pH as the [A^–] increases. Since A^– is the conjugate base of HA (see equation below), by increasing the concentration of A^–, the equilibrium will favour HA (based on Le Chatelier’s Principle) thereby decreasing the [H₃O⁺] in solution and therefore increasing the pH. Later in this chapter, the Henderson-Hasselbach equation will be introduced and will mathematically demonstrate why pH = pK_a when [HA] = [A-].

(b) Since we are adding base, it will be neutralized by the acid of the buffer, acetic acid. First, we calculate the concentrations of an intermediate mixture resulting from the complete reaction between the acid in the buffer and the added base. Then we determine the concentrations of the mixture at the new equilibrium:

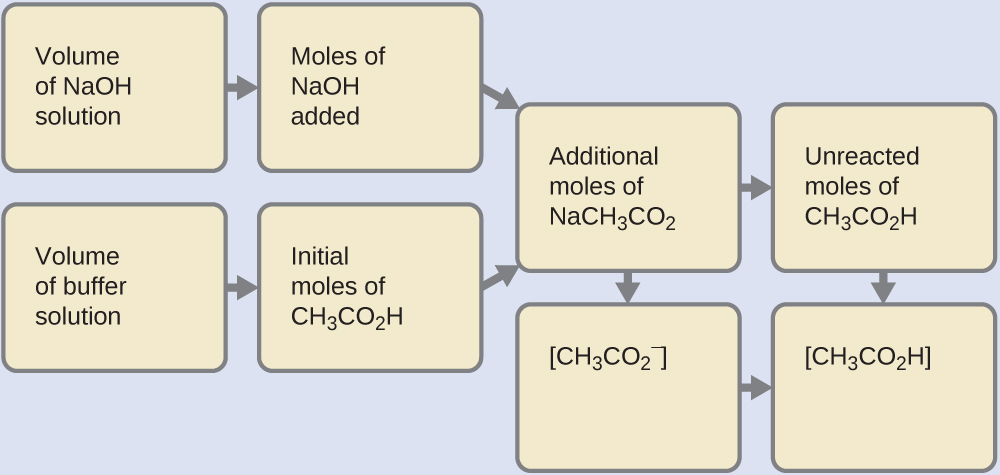
Determine the moles of NaOH. One milliliter (0.0010 L) of 0.10 M NaOH contains:

0.0010 L×(0.10 mol NaOH/1 L) = 1.0×10^–4 mol NaOH

Determine the moles of CH₂CO₂H. Before reaction, 0.100 L of the buffer solution contains:

0.100 L ×(0.100 mol CH₃CO₂H/1L) = 1.00×10^-2 mol CH₃CO₂H

Solve for the amount of NaCH₃CO₂ produced. The 1.0×10⁻⁴ mol of NaOH neutralizes 1.0×10⁻⁴ mol of CH₃CO₂H, leaving:

(1.0×10^-2)-(0.01×10^-2) = 0.99×10^-2 mol CH₃CO₂H

and producing 1.0 × 10⁻⁴ mol of NaCH₃CO₂. This makes a total of:

(1.0×10^-2)+(0.01×10^-2) = 1.01×10^-2 mol NaCH₃CO₂

Find the molarity of the products. After reaction, CH₃CO₂H and NaCH₃CO₂ are contained in 101 mL of the intermediate solution, so:

Now we calculate the pH after the intermediate solution, which is 0.098 M in CH₃CO₂H and 0.100 M in NaCH₃CO₂, comes to equilibrium. The calculation is very similar to that in part (a) of this example:

This series of calculations gives a pH = 4.75. Thus the addition of the base only slightly increased the pH of the solution from 4.74 to 4.75.

(c) Since HCl is a strong acid, it ionizes completely, forming 1.8×10–5 M H3O+ – notice that this dilute, unbuffered solution of HCl has the same hydronium ion concentration as the acetic acid-acetate buffer solution described in part (a). Therefore, we can deduce that the starting pH of the HCl solution is identical, 4.74.

First, we determine the number of moles of HCl present: 

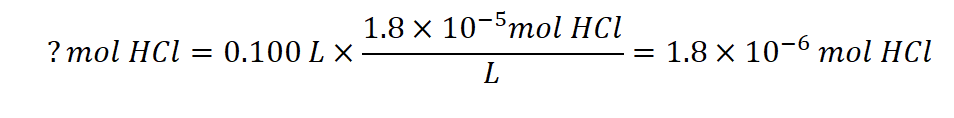
As shown in part (b), 1 mL of 0.10 M NaOH contains 1.0 × 10⁻⁴ mol of NaOH. When the NaOH and HCl solutions are mixed, the HCl is the limiting reagent in the reaction. All of the HCl reacts, and the amount of NaOH that remains is:

                  mol NaOH leftover= total mol- reacted mol

(1.0×10^-4)-(1.8×10^-6) = 9.8×10^-5 M

The concentration of NaOH is:

9.8×10^-5 M NaOH/0.101L= 9.7×10^-4 M

The pOH of this solution is:

pOH = -log[OH^–] = -log(9.7×10^-4) = 3.01

The pH is:

pH = 14.00-pOH = 10.99

The pH changes from 4.74 to 10.99 in this unbuffered solution. This drastically differs from to the change of 4.74 to 4.75 that occurred when the same amount of NaOH was added to the buffered solution described in part (b).

Check Your Learning 6.2.1 – pH Changes in Buffered and Unbuffered Solutions

Show that adding 1.0 mL of 0.10 M HCl changes the pH of 100 mL of a 1.8 × 10⁻⁵ M HCl solution from 4.74 to 3.00.

Solution

Initial pH of 1.8 × 10⁻⁵ M HCl:

pH = −log[H₃O⁺] = −log[1.8 × 10⁻⁵] = 4.74

Moles of H₃O⁺ in 100 mL of 1.8 × 10⁻⁵ M HCl:

1.8 × 10⁻⁵ mol/L × 0.100 L = 1.8 × 10⁻⁶ mol

Moles of H₃O⁺ added by addition of 1.0 mL of 0.10 M HCl:

0.10 mol/L × 0.0010 L = 1.0 × 10⁻⁴ mol

Final pH after addition of 1.0 mL of 0.10 M HCl:

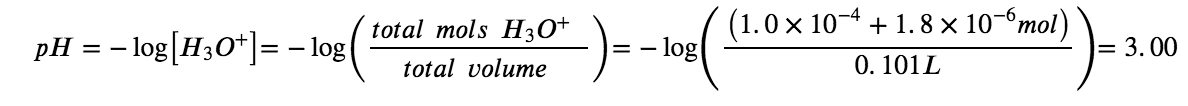
Selection of Suitable Buffer Mixtures

There are two useful rules of thumb for selecting buffer mixtures:

1. A good buffer mixture should have about equal concentrations of both of its components.

2. A buffer solution has generally lost its usefulness when the amount of one component of the buffer pair is less than about 10% of the other. Figure 6.2.2 shows the effect on the pH of an acetic acid-acetate ion buffer as the amount of strong base is added. Initially, the buffer contains equal amounts of acetic acid and acetate, and the initial pH is 4.74. A change of 1 pH unit occurs when the acetic acid concentration is reduced to 11% of the acetate ion concentration.

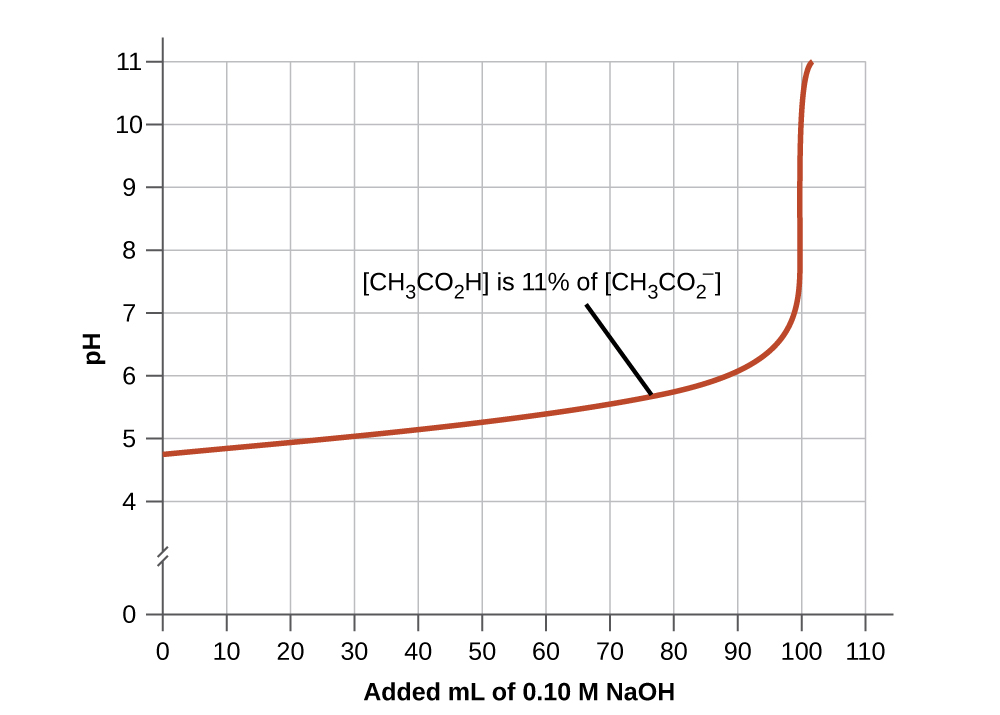
Figure 6.2.2. The graph, an illustration of buffering action, shows change of pH as an increasing amount of a 0.10 M NaOH solution is added to 100 mL of a buffer solution in which, initially, [CH₃CO₂H] = 0.10 M and [CH₃CO₂⁻] = 0.10 M.

3. Weak acids and their conjugate bases are better as buffers for pHs less than 7; weak bases and their conjugate acids are better as buffers for pHs greater than 7.

The Henderson-Hasselbalch Equation

The ionization-constant expression for a solution of a weak acid can be written as:

K_a = ([H₃O⁺][A^–])/[HA]

Rearranging to solve for [H₃O⁺], we get:

[H₃O⁺] = K_a×([HA]/[A^–])

Taking the negative logarithm of both sides of this equation, we arrive at:

-log[H₃O⁺] = -log(K_a)-log([HA]/[A^–])

which can be written as:

pH = pK_a+log([A^–]/[HA])

where pK_a is the negative of the common logarithm of the ionization constant of the weak acid (pK_a = −log(K_a)). This equation relates the pH, the ionization constant of a weak acid, and the concentrations of the weak acid and its conjugate base in a buffered solution. Scientists often use this expression, called the Henderson-Hasselbalch equation, to calculate the pH of buffer solutions. It is important to note that the “x is small” assumption must be valid to use this equation.

Medicine: the Buffer System in Blood

Blood is an important example of a buffered solution, with the principal acid and ion responsible for the buffering action being carbonic acid, H₂CO₃, and the bicarbonate ion, HCO₃⁻. When an excess of hydrogen ion enters the bloodstream, it is removed primarily by the reaction:

H₃O⁺ (aq) + HCO₃^– (aq) → H₂CO₃ (aq) + H₂O (l)

When an excess of the hydroxide ion is present, it is removed by the reaction:

OH^– (aq) + H₂CO₃ (aq) → HCO₃^– (aq) + H₂O (l)

The concentration of carbonic acid, H₂CO₃ is approximately 0.0012 M, and the concentration of the hydrogen carbonate ion, HCO₃−, is around 0.024 M. Using the Henderson-Hasselbalch equation and the pK_a of carbonic acid at body temperature, we can calculate the pH of blood:

pH = pK_a+log([base]/[acid]) = 6.4+log(0.024/0.0012) = 7.7

The fact that the H₂CO₃ concentration is significantly lower than that of the HCO₃⁻ ion may seem unusual, but this imbalance is due to the fact that most of the by-products of our metabolism that enter our bloodstream are acidic. Therefore, there must be a larger proportion of base than acid, so that the capacity of the buffer will not be exceeded.

Lactic acid is produced in our muscles when we exercise. As the lactic acid enters the bloodstream, it is neutralized by the HCO₃⁻ ion, producing H₂CO₃. An enzyme then accelerates the breakdown of the excess carbonic acid to carbon dioxide and water, which can be eliminated by breathing. In fact, in addition to the regulating effects of the carbonate buffering system on the pH of blood, the body uses breathing to regulate blood pH. If the pH of the blood decreases too far, an increase in breathing removes CO₂ from the blood through the lungs driving the equilibrium reaction such that [H₃O⁺] is lowered. If the blood is too alkaline, a lower breath rate increases CO₂ concentration in the blood, driving the equilibrium reaction the other way, increasing [H⁺] and restoring an appropriate pH.

Buffer Range and Buffer Capacity

Buffers are characterized by two parameters, buffer range and buffer capacity. Buffer range is the interval of pH values over which a buffer can reliably neutralize added external acids/bases. It is equal to pK_a ± 1, and is thus a function of the identity of the acid in the conjugate acid/base pair used to construct the buffer. For example, the pK_a of acetic acid is 4.74; therefore, buffers made by mixing acetic acid and acetate can have pH’s ranging from 3.74 up to 5.74. This is a consequence of the second requirement for buffers mentioned above: one component cannot be present in an amount that is less than 10% of the other, or:

1/10 < [base]/[acid] < 10/1

In other words, the ratio of base-to-acid in the buffer, must be greater than 0.1 but less than 10. As soon as this ratio becomes too lopsided (i.e. outside the above interval), then the buffer range has been exceeded, and we no longer expect the mixture to neutralize external acids/bases effectively.

Buffer solutions do not have an unlimited capacity to keep the pH relatively constant (Figure 6.2.3). If we add so much base to a buffer that the weak acid is exhausted, no more buffering action toward the base is possible. On the other hand, if we add an excess of acid, the weak base would be exhausted, and no more buffering action toward any additional acid would be possible. In fact, we do not even need to exhaust all of the acid or base in a buffer to overwhelm it; its buffering action will diminish rapidly as a given component nears depletion.

Figure 6.2.3. The indicator colour (methyl orange) shows that a small amount of acid added to a buffered solution of pH 8 (beaker on the left) has little effect on the buffered system (middle beaker). However, a large amount of acid exhausts the buffering capacity of the solution and the pH changes dramatically (beaker on the right). (credit: modification of work by Mark Ott)

The buffer capacity therefore is the amount of acid or base that can be added to a given volume of a buffer solution before the pH changes significantly, usually by one unit. Buffer capacity depends on the amounts of the weak acid and its conjugate base that are in a buffer mixture.

The more concentrated the buffer solution, the greater its buffer capacity. As illustrated in Figure 6.2.4, when NaOH is added to solutions that contain different concentrations of an acetic acid/sodium acetate buffer, the observed change in the pH of the buffer is inversely proportional to the concentration of the buffer. If the buffer capacity is 10 times larger, then the buffer solution can absorb 10 times more strong acid or base before undergoing a significant change in pH.

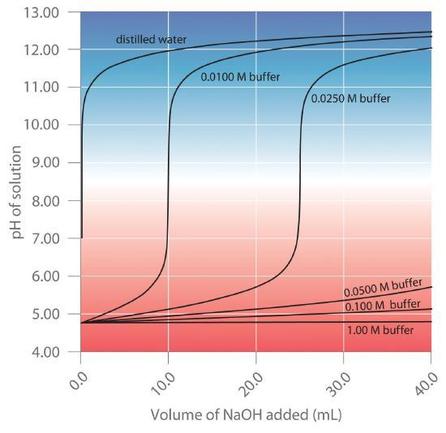
Figure 6.2.4. Effect of Buffer Concentration on the Capacity of a Buffer.