5.4 – Polyprotic Acids
We can classify acids by the number of protons per molecule that they can give up in a reaction. Acids such as HCl, HNO3, and HCN that contain one ionizable hydrogen atom in each molecule are called monoprotic acids. Their reactions with water are:
HCl (aq) + H2O (l) → H3O+ (aq) + Cl– (aq)
HNO3 (aq) + H2O (l) →H3O+ (aq) + NO3– (aq)
HCN (aq) + H2O (l) ⇌ H3O+ (aq) + CN– (aq)
Note: the Ka of HCN is 6.2 x 10-10. This means that the acid does not fully ionize in water and necessitates the equilibrium arrow.
Even though it contains four hydrogen atoms, acetic acid, CH3CO2H, is also monoprotic because only the hydrogen atom from the carboxylic acid functional group (COOH) reacts with bases:
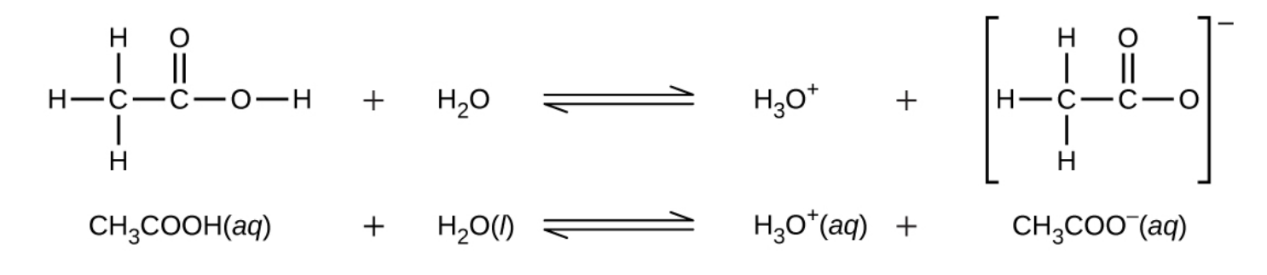
Similarly, monoprotic bases are bases that will accept a single proton.
|
|
Diprotic Acids
Diprotic acids contain two ionizable hydrogen atoms per molecule; ionization of such acids occurs in two steps. The first ionization always takes place to a greater extent than the second ionization. For example, sulfuric acid, a strong acid, ionizes as follows:
First ionization: H2SO4 (aq) + H2O (l) ⇌ H3O+ (aq) + HSO4– (aq)
For this reaction, Ka1 > 102, indicating ~100% complete ionization of the first proton.
Second ionization: HSO4– (aq) + H2O (l) ⇌ H3O+ (aq) + SO42- (aq)
For this reaction, Ka2 = 1.0×10−2, indicating that the second ionization is only partial.
This stepwise ionization process occurs for all polyprotic acids. When we make a solution of a weak diprotic acid, we get a solution that contains a mixture of acids. Carbonic acid, H2CO3, is an example of a weak diprotic acid. The first ionization of carbonic acid yields hydronium ions and bicarbonate ions in small amounts.
First ionization: H2CO3 (aq) + H2O (l) ⇌ H3O+ (aq) + HCO3– (aq)
Second ionization: HCO3– (aq) + H2O (l) ⇌ H3O+ (aq) + CO32- (aq)
Let’s confirm this very important concept mathematically. The ICE tables below display both ionization reactions, starting with a 10.0 M solution of H2CO3. Notice that with the first ionization reaction, we generate a small concentration of H3O+ and HCO3– (even starting with 10.0 M of H2CO3!) – this is again due to the relatively small Ka1 value. Afterwards, the second ionization reaction which has an even smaller Ka2 value practically causes no change in the concentration of HCO3– and H3O+ and generates a negligible amount of CO32-.
|
1ST IONIZATION: H2CO3(aq) + H2O(aq) ⇌ H3O+(aq) + HCO3–(aq) |
|||
|
|
[H2CO3] |
[H3O+] |
[HCO3–] |
| Initial concentration (M) |
10.0 |
0.0 |
0.0 |
| x = 0.0021 M | |||
| Change (M) |
10.0 – 0.0021 |
0.0 + 0.0021 |
0.0 + 0.0021 |
| Equilibrium concentration (M) |
9.9979 |
0.0021 |
0.0021 |
|
2ND IONIZATION: HCO3–(aq) + H2O(aq) ⇌ H3O+(aq) + CO32-(aq) |
|||
|
|
[HCO3–] |
[H3O+] |
[CO32-] |
|
Initial concentration (M) |
0.0021 |
0.0021 |
0.0 |
| x = 4.7 × 10-11 M | |||
|
Change (M) |
0.0021 – 4.7 × 10-11 |
0.0021 + 4.7 × 10-11 |
0.0 + 4.7 × 10-11 |
|
Equilibrium concentration (M) |
~0.0021 |
~0.0021 |
~0.0 |
If the first ionization constant of a weak diprotic acid is larger than the second by a factor of at least 20, it is appropriate to treat the first ionization separately and calculate concentrations resulting from it before calculating concentrations of species resulting from subsequent ionization. This can simplify our work considerably because we can determine the concentration of H3O+ and the conjugate base from the first ionization, then determine the concentration of the conjugate base of the second ionization in a solution with concentrations determined by the first ionization.
Example 5.4.1 – Ionization of a Diprotic Acid
When we buy soda water (carbonated water), we are buying a solution of carbon dioxide in water. The solution is acidic because CO2 reacts with water to form carbonic acid, H2CO3. What are [H3O+], [HCO3−], and [CO32−] in a saturated solution of CO2 with an initial [H2CO3] = 0.033 M?
H2CO3 (aq) + H2O (l) ⇌ H3O+ (aq) + HCO3– (aq) Ka1 = 4.5 x 10-7
HCO3– (aq) + H2O (l) ⇌ H3O+ (aq) + CO32- (aq) Ka2 = 4.7 x 10-11
Solution
As indicated by the ionization constants, H2CO3 is a much stronger acid than HCO3−, so H2CO3 is the dominant producer of hydronium ions in solution. Thus there are two parts in the solution of this problem: (1) Using the customary four steps, we determine the concentration of H3O+ and HCO3− produced by ionization of H2CO3. (2) Then we determine the concentration of CO32− in a solution with the concentration of H3O+ and HCO3− determined in (1). To summarize:
Determine the concentrations of H3O+ and HCO3−.
H2CO3 (aq) + H2O (l) ⇌ H3O+ (aq) + HCO3– (aq) Ka1 = 4.5 x 10-7
As for the ionization of any other weak acid:

An abbreviated table of changes and concentrations shows:
H2CO3 + H2O⇌ H3O+ + HCO3–
| H2CO3 | H2O | H3O+ | HCO3– | |
| Initial Concentration (M) | 0.033 | / | ~0 | 0 |
| Change (M) | – x | / | x | x |
| Equilibrium concentration (M) | 0.033 – x | / | x | x |
Substituting the equilibrium concentrations into the equilibrium gives us:
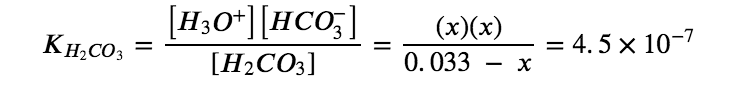
Solving the preceding equation making our standard assumptions gives:
x=1.2×10-4
Thus:
[H2CO3]=0.033 M
[H3O+]=[HCO3–]=1.2×10-4 M
Determine the concentration of CO32− in a solution at equilibrium with [H3O+] and [HCO3−] both equal to 1.2 × 10−4 M.
HCO3– (aq) + H2O (l) ⇌ H3O+ (aq) + CO32- (aq)
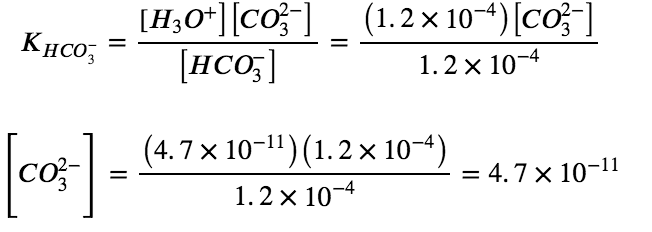
To summarize: In part 1 of this example, we found that the H2CO3 in a 0.033 M solution ionizes slightly and at equilibrium [H2CO3] = 0.033 M; [H3O+] = 1.2 × 10−4 M; and [HCO3−] = 1.2×10−4 M. In part 2, we determined that [CO32−] = 4.7×10−11 M.
Check Your Learning 5.4.1 – Ionization of a Diprotic Acid
The concentration of H2S in a saturated aqueous solution at room temperature is approximately 0.1 M. Calculate [H3O+], [HS−], and [S2−] in the solution:
H2S (aq) + H2O (l) ⇌ H3O+ (aq) + HS– (aq) Ka1 = 8.9 x 10-8
HS– (aq) + H2O (l) ⇌ H3O+ (aq) + S2- (aq) Ka2 = 1.0 x 10-19
Answer
[H2S] = 0.1 M; [H3O+] = [HS−] = 0.000094 M; [S2−] = 1 × 10−19 M ≈ 0 M
We note that the concentration of the sulfide ion is the same as Ka2. This is due to the fact that each subsequent ionization of a polyprotic acid occurs to a lesser degree.
Triprotic Acids
A triprotic acid is an acid that has three ionizable protons that undergo stepwise ionization: Phosphoric acid is a typical example:
First ionization: H3PO4 (aq) + H2O (l) ⇌ H3O+ (aq) + H2PO4– (aq) Ka1 = 7.5 x 10-3
Second ionization: H2PO4– (aq) + H2O (l) ⇌ H3O+ (aq) + HPO42- (aq) Ka2 = 6.2 x 10-5
Third ionization: HPO42– (aq) + H2O (l) ⇌ H3O+ (aq) + PO43- (aq) Ka3 = 4.2 x 10-13
As with the diprotic acids, the differences in the ionization constants of these reactions tell us that in each successive step the degree of ionization is significantly weaker. This is a general characteristic of polyprotic acids and successive ionization constants often differ by a factor of about 105 to 106.
This set of three ionization reactions may appear to make calculations of equilibrium concentrations in a solution of H3PO4 complicated. However, because the successive ionization constants differ by a factor of 105 to 106, the calculations can be broken down into a series of parts similar to those for diprotic acids.
Polyprotic Bases
Polyprotic bases can accept more than one hydrogen ion in solution. The carbonate ion is an example of a diprotic base, since it can accept up to two protons. Solutions of alkali metal carbonates are quite alkaline, due to the reactions:
First protonation:
H2O (l) + CO32- (aq) ⇌ HCO3– (aq) + OH– (aq) Kb1 = Kw/Ka2= 2.1 × 10-4
Second protonation:
H2O (l) + HCO3– (aq) ⇌ H2CO3 (aq) + OH– (aq) Kb2 = Kw/Ka1= 2.2 × 10-8
Example 5.4.2 – Converting Between Ka and Kb – Polyprotic Acids-Bases
Given the following chemical equilibrium reaction, which of the following expressions correctly describes its equilibrium constant, K:
PO43- + H2O ⇌ OH– + HPO4–
(a) 1/Ka2
(b) Kw/Ka3
(c) 1/Ka3
(d) Kw/Ka2
Solution
Notice how in this reaction, the main species PO43- accepts a proton as it reacts with water – this means that it is the base in this reaction and hence, K is more specifically Kb. Recall that, for any conjugate acid-base pair, the relationship between Ka and Kb is: Kw = Ka × Kb. We can already rule out options (a) and (c) since they do not include Kw in the expression for K.
The reaction indicated starts with a phosphate ion (which is non-protonated) that is converted into its conjugate monoprotic acid HPO4–. PO43- is in its most deprotonated form (no protons), so this reaction is Kb1 – the first reaction in which PO43- picks up its very first proton. With that in mind, we can say that this reaction corresponds to Ka3. Since we’re working with HPO4– as the acid and PO43- as its conjugate base, this equilibrium can be seen in one of two ways: either we have PO43- as the base reacting with water to pick it up its very first proton and become HPO43- (which is Kb1), or we have HPO43- as the acid reacting with water to lose its last proton and become PO43- (which is Ka3). We can see that both (b) and (d) both have the expression arranged correctly such that Kw/Ka = Kb, however, only (b) uses Ka3 to correctly convert to Kb1.
Therefore, the correct answer is (b).
Check Your Learning 5.4.2 – Converting Between Ka and Kb – Polyprotic Acids-
Bases
Given the information below, give the balanced chemical equations and calculate the equilibrium constants for the 3 successive protonation reactions of the hypothetical base, A3– (aq).
H3A (aq) + H2O (l) ⇌ H3O+ (aq) + H2A– (aq) Ka1 = 1.5 x 10-4
H2A– (aq) + H2O (l) ⇌ H3O+ (aq) + HA2– (aq) Ka2 = 2.7 x 10-9
HA2– (aq) + H2O (l) ⇌ H3O+ (aq) + A3– (aq) Ka3 = 8.8 x 10-12
Answer:
A3– (aq) + H2O (l) ⇌ OH– (aq) + HA2– (aq) Kb1 = KW/Ka3 = 1.1 x 10-3
HA2– (aq) + H2O (l) ⇌ OH– (aq) + H2A– (aq). Kb2 = KW/Ka2 = 3.7 x 10-6
H2A– (aq) + H2O (l) ⇌ OH– (aq) + H3A (aq) Kb3 = KW/Ka1 = 6.7 x 10-11
Questions
★ Questions
- Which of the following concentrations would be practically equal in a calculation of the equilibrium concentrations in a 0.134 M solution of H2CO3, a diprotic acid: [H3O+], [OH−], [H2CO3], [HCO3−], [CO32−]? No calculations are needed to answer this question.
2. Calculate the concentration of each species present in a 0.050 M solution of H2S.
3. Calculate the concentration of each species present in a 0.010 M solution of phthalic acid, C6H4(CO2H)2.
C6H4(CO2H)2(aq)+H2O(l)↔H3O(aq)++C6H4(CO2H)(CO2)(aq)– Ka=1.1×10-3
C6H4(CO2H(CO2)(aq)-+H2O(l)↔H3O(aq)++C6H4(CO2)2(aq)2- Ka=3.9×10-6
★★ Questions
4. Salicylic acid, HOC6H4CO2H, and its derivatives have been used as pain relievers for a long time. Salicylic acid occurs in small amounts in the leaves, bark, and roots of some vegetation (most notably historically in the bark of the willow tree). Extracts of these plants have been used as medications for centuries. The acid was first isolated in the laboratory in 1838.
(a) Both functional groups of salicylic acid ionize in water, with Ka = 1.0 × 10−3 for the—CO2H group and 4.2 × 10−13 for the −OH group. What is the pH of a saturated solution of the acid (solubility = 1.8 g/L).
(b) Aspirin was discovered as a result of efforts to produce a derivative of salicylic acid that would not be irritating to the stomach lining. Aspirin is acetylsalicylic acid, CH3CO2C6H4CO2H. The −CO2H functional group is still present, but its acidity is reduced, Ka = 3.0 × 10−4. What is the pH of a solution of aspirin with the same concentration as a saturated solution of salicylic acid (See Part a).
(c) Under some conditions, aspirin reacts with water and forms a solution of salicylic acid and acetic acid:
CH3CO2C6H4CO2H (aq) + H2O (l) ⇌ HOC6H4CO2H (aq) + CH3CO2H (aq)
(i) Which of the acids, salicylic acid or acetic acid, produces more hydronium ions in such a solution?
(ii) What are the concentrations of molecules and ions in a solution produced by the hydrolysis of 0.50 g of aspirin dissolved in enough water to give 75 mL of solution?
5. The ion HTe− is an amphiprotic species; it can act as either an acid or a base.
(a) What is Ka for the acid reaction of HTe− with H2O?
(b) What is Kb for the reaction in which HTe− functions as a base in water?
(c) Demonstrate whether or not the second ionization of H2Te can be neglected in the calculation of [HTe−] in a 0.10 M solution of H2Te.
Answers
- [H3O+] and [HCO3−] are practically equal.
2. [HS] = 7.1 x 10−5 M, [H3O+] = 7.1 x 10−5 M, [S−2] = 1.29 x 10−13 M, [H2S] = 0.0499 M
[C6H4(CO2)22-(aq)]=3.9×10-6 M, [OH-]=3.6×10-12 M
4. (a) pH = 2.44, (b) pH = 2.70, (c) (i) salicylic acid (ii) The concentration of aspirin and acetic acid is 2.1 x 10−4 M
5. (a) Ka2=1.5×10-11
(b) Kb=4.3×10-12
(c) ([Te2-][H3O+(aq)])/[HTe–]=((x)(0.0141+x))/(0.0141-x)≈((x)(0.0141))/(0.0141)=1.5×10-11
Solving for x gives 1.5×10-11 M. Therefore, compared with 0.014 M, this values is negligible (1.1×10-7%)
Acid containing one ionizable hydrogen atom per molecule
Acid containing two ionizable hydrogen atoms per molecule
Process in which a polyprotic acid is ionized by losing protons sequentially

 NOTE: Ionizable (also known as acidic) protons are typically written at the beginning of a condensed chemical formula. Examples of this include H2SO4, which is diprotic, and H3PO4, which is triprotic. Occasionally, some chemical formulae do not follow this pattern. This is usually due to historical reasons where the chemical formula has been written a certain way for several years. For example, acetic acid can be written HC2H3O2, CH3CO2H, or CH3COOH. When in doubt, check the literature for the correct formula.
NOTE: Ionizable (also known as acidic) protons are typically written at the beginning of a condensed chemical formula. Examples of this include H2SO4, which is diprotic, and H3PO4, which is triprotic. Occasionally, some chemical formulae do not follow this pattern. This is usually due to historical reasons where the chemical formula has been written a certain way for several years. For example, acetic acid can be written HC2H3O2, CH3CO2H, or CH3COOH. When in doubt, check the literature for the correct formula.