5.3 – Acid-Base Strength

We can rank the strengths of acids by the extent to which they ionize in aqueous solution. The reaction of an acid with water is given by the general expression:

HA (aq) + H₂O (aq) ⇌ H₃O⁺ (aq) + A^– (aq)

Water is the base that reacts with the acid HA, A⁻ is the conjugate base of the acid HA, and the hydronium ion is the conjugate acid of water. A strong acid yields 100% of H₃O⁺ and A⁻ when the acid ionizes in water; Figure 5.3.1 lists several strong acids. If we start with 0.1 M HCl, at equilibrium we get 0.1 M H₃O⁺ and 0.1 M Cl^–. Based on the Brønsted-Lowry definition, as a strong acid, HCl is a very good proton donor. For a reaction of a strong acid with water, the general chemical equation above applies, except the equilibrium symbol is usually replaced with a one-way arrow to indicate that the reaction goes entirely to completion:

HA (aq) + H₂O (l) → H₃O⁺ (aq) + A^– (aq)

A weak acid gives amounts of H₃O⁺ and A⁻ that represent much less than 100% ionization. Hence, referring back to the Brønsted-Lowry definition, we can say that weak acids are poor proton donors.

For a reaction of a weak acid with water, the general chemical equation first indicated in this section applies – we use an equilibrium arrow to indicate that the reaction isn’t to completion and that at equilibrium both reactants are products are present:

HA (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + A^– (aq)

Figure 5.3.1. Some of the common strong acids and bases are listed here.

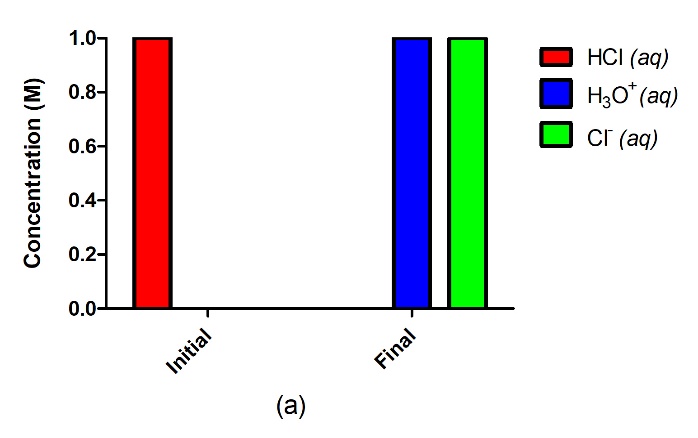
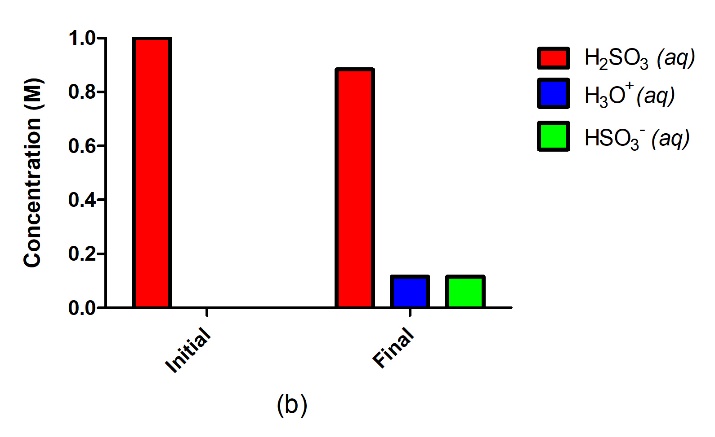
Figure 5.3.2.A strong acid such as HCl in water (a) will completely ionize and go to completion with no reactant remaining, where 1.0 M of HCl will yield 1.0 M H₃O⁺ and 1.0 M Cl^–. A weak acid such as H₂SO₃ (b), on the other hand, will only partially ionize in water, giving us an equilibrium mixture of reactants and products.

If you recall back to the previous chapter on chemical equilibria, you’ll notice that this notion of ratio of products to reactants is exactly how we express equilibrium constants! Therefore, we can use this knowledge to determine the relative strengths of acids by measuring their equilibrium constants in aqueous solutions. In solutions of the same concentration, stronger acids ionize completely, and so yield higher concentrations of hydronium ions than do weaker acids. When writing an equation for the ionization of a strong acid, a one-way arrow is used in order to show that it is a complete reaction. While any acid with less than 100% ionization is technically classified as a ‘weak acid’, for most weak acids, at equilibrium only a very small fraction of the acid will ionize. The equilibrium constant for an acid is called the acid-ionization constant, K_a. For the reaction of an acid HA:

HA (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + A^– (aq)

we write the equation for the ionization constant as:

K_a = ([H₃O⁺][A^–])/[HA]

where the concentrations are those at equilibrium. Recall from Chapter 4 that although water is a reactant in the reaction, it is a liquid, its activity is equal to 1, and thus it does not appear in the K_a expression. The larger the K_a of an acid, the larger the concentration of H₃O⁺ and A⁻ relative to the concentration of the neutral, unionized acid, HA. Thus a stronger acid has a larger ionization constant than a weaker acid, and the ionization constants increase as the strengths of the acids increase. Table 5.3.1, found later in this section, lists values of ionization constants of a few common weak acids; a more complete table of K_a values can be found in Appendix H.

To illustrate, consider the three acid equilibria below: the acid-ionization constants indicate that the order of acid strength for these acids is: CH₃CO₂H < HNO₂ < HSO₄⁻.

CH₃CO₂H (aq) + H₂O (aq) → H₃O⁺ (aq) + CH₃CO₂^– (aq) K_a = 1.8 x 10^–5

HNO₂ (aq) + H₂O (l) → H₃O⁺ (aq) + NO₂^– (aq) K_a = 4.6 x 10^–4

HSO₄^– (aq) + H₂O (l) → H₃O⁺ (aq) + SO₄^2- (aq) K_a = 1.2 x 10^–2

Another measure of the strength of an acid is its percent ionization. The percent ionization of a weak acid is the ratio of the concentration of the ionized acid to the initial acid concentration, times 100:

%ionization = ([H₃O⁺]_eq/[HA]₀]×100%

Because the ratio includes the initial concentration, the percent ionization for a solution of a given weak acid varies depending on the original concentration of the acid, and actually decreases with increasing acid concentration…but why?

Let’s take a look back at the equilibrium for acid ionization, again using HA as our generic weak acid with a K_a value of 1.00×10^–5:

HA (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + A^– (aq) K_a = 1.00 x 10^–5

Imagine we have 1 L of water and we add exactly 0.100 mol of this weak acid, giving an initial value of [HA]₀ = 0.100 M. Following the ICE table method shown in Chapter 4, we find that, at equilibrium, the solution contains 0.00100 M H₃O⁺, resulting in a percent ionization of exactly 1.0% (take a moment to confirm this calculation for yourself). Now imagine we increase the amount of initial acid, by adding another 0.100 mol to the existing solution, giving a total of 0.200 mol HA in 1 L of water, thus [HA]₀ = 0.200 M. This second addition of 0.100 mol HA is trying to ionize in a solution that already contains 0.00100 M H₃O⁺ produced from the first 0.100 mol of HA added. According to Le Chatelier’s Principle, increasing the amount of a product shifts the equilibrium towards reactants. Therefore, trying to produce H₃O⁺ in a solution that already contains some H₃O⁺ is disfavoured. In other words, the presence of some H₃O⁺ from the first addition of 0.100 mol HA inhibits the ionization of the second addition of 0.100 mol HA. We can confirm this by redoing our ICE table calculation: a value of [HA]₀ = 0.200 M yields an equilibrium concentration of 0.00141 M H₃O⁺ and a percent ionization of 0.71% (again, you should confirm these values yourself). Notice how the total amount of H₃O⁺ at equilibrium has indeed increased (because we added more HA), but the fraction that ionized has gotten smaller: this is Le Chatelier’s Principle in action!

This is a very important concept, so it is prudent to emphasize it again, as illustrated in Figure 5.3.3 below. This figure shows the percent ionization and the equilibrium concentration of H₃O⁺ for the ionization of nitrous acid, HNO₂:

HNO₂ (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + NO₂^– (aq) K_a = 5.6 x 10^–4

Increasing the initial concentration of HNO₂ will increase the amount of H₃O⁺ produced at equilibrium. However, as we add more and more nitrous acid, we further inhibit the ionization, instead favouring the reverse reaction. Therefore, what is being directly affected isn’t the final equilibrium concentration of H₃O⁺ (which keeps increasing) but rather the actual extent of acid ionization – what fraction of the acid actually ionizes successfully in solution. So, in conclusion, as [HNO₂]₀ increases, [H₃O⁺]_eq increases, but the percent ionization of HNO₂ decreases.

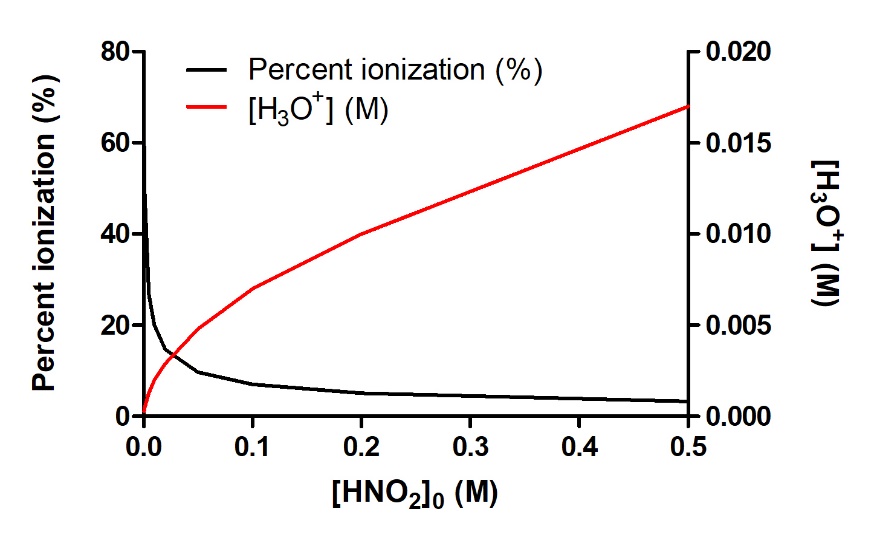
Figure 5.3.3.As the concentration of HNO₂ increases in aqueous solution, the concentration of H₃O⁺ produced increases as well; however, the fraction of the original concentration that is ionizing is decreasing, as indicated by the decrease in percent ionization.

Try it For Yourself – Percent Ionization and [H₃O⁺]_eq against Initial Acid Concentration

The K_a value for benzoic acid is approximately 6.25 × 10^-5. The equilibrium equation for the ionization of benzoic acid is as follows:

C₆H₅COOH_(aq) + H₂O_(l) ⇌ C₆H₅COO^–_(aq) + H₃O⁺_(aq)

Assume that K_a is constant and that you only initially start with reactant (i.e. benzoic acid). Using a spreadsheet software (e.g. Microsoft Excel, Google Sheets):

Determine [H₃O⁺]_eq and the percent ionization at the following initial concentrations of benzoic acid: 0.005 M, 0.010 M, 0.020 M, 0.025 M, 0.050 M, 0.075 M, 0.10 M, 0.25 M, 0.5 M, 1.0 M. (Hint: Recall that acid ionization is an equilibrium reaction…use equilibrium-reaction problem solving to assist you).

Using this data, plot a graph of [C₆H₅COOH]₀ (initial concentration of benzoic acid) versus [H₃O⁺]_eq on one y-axis and percent ionization on another y-axis.

Do you notice any trends? Can you explain them?

Example 5.3.1 – Calculation of Percent Ionization from pH

Calculate the percent ionization of a 0.125 M solution of nitrous acid (a weak acid), with a pH of 2.09.

Solution

The percent ionization for an acid is:

([H₃O⁺]_eq/[HNO₂]₀)×100%

The chemical equation for the ionization of the nitrous acid is:

HNO₂ (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + NO₂^– (aq) K_a = 5.6 x 10^–4

Since 10^−pH = [H₃O⁺], we find that 10^−2.09 = 8.1 × 10⁻³ M, so that percent

ionization is:

8.1×10^-30.125×100%=6.5%

Remember, the logarithm 2.09 indicates a hydronium ion concentration with only two significant figures.

Check Your Learning 5.3.1 – Calculation of Percent Ionization from pH

Calculate the percent ionization of a 0.10 M solution of acetic acid with a pH of 2.89.

Answer

1.3% ionized

We can rank the strengths of bases by their tendency to form hydroxide ions in aqueous solution. The general reaction of a Brønsted-Lowry base with water is given by:

B (aq) + H₂O (l) → HB⁺ (aq) + OH^– (aq)

Water is the acid that reacts with the base, HB⁺ is the conjugate acid of the base B, and the hydroxide ion is the conjugate base of water. A strong base yields 100% (or very nearly so) of OH⁻ and HB⁺ when it reacts with water; Figure 5.3.1. lists several strong bases. Based on the Brønsted-Lowry definition, we could characterize strong bases as being very good proton acceptors (i.e. they have a high tendency to accept protons from acids). A weak base yields a small proportion of hydroxide ions and is thus a poor proton acceptor. Soluble ionic hydroxides such as NaOH are considered strong bases because they ionize completely when dissolved in water. You can view a PhET simulation of strong and weak acids and bases at the molecular level by clicking here.

As we did with acids, we can measure the relative strengths of bases by measuring their base-ionization constant (K_b) in aqueous solutions. In solutions of the same concentration, stronger bases ionize to a greater extent, and so yield higher hydroxide ion concentrations than do weaker bases. A stronger base has a larger ionization constant than does a weaker base. For the reaction of a base, B:

B (aq) + H₂O (l) → HB⁺ (aq) + OH^– (aq)

we write the equation for the ionization constant as:

K_b = ([HB⁺][OH^–])/[B]

where the concentrations are those at equilibrium. Again, we do not include H₂O in the equation because water is a liquid with an activity equal to 1. Like K_a values, there is a wide range of known K_b values, as shown in the three examples below:

NO₂^– (aq) + H₂O (l) ⇌ HNO₂ (aq) + HO^– (aq) K_b = 2.22 x 10^–11

CH₃CO₂^– (aq) + H₂O (l) ⇌ CH₃CO₂H (aq) + OH^– (aq) K_b = 5.6 x 10^–10

NH₃ (aq) + H₂O (l) ⇌ NH₄⁺ (aq) + OH^– (aq) K_b = 1.8 x 10^-5

Table 5.3.1, found later in this section, lists values of ionization constants of a few common weak bases; a more complete table of K_b values can be found in Appendix I.

As with acids, percent ionization can be measured for basic solutions, but, as explained above, this value will vary depending on the base ionization constant and the initial concentration of the solution.

Equilibrium Constants and Conjugate Pairs

Consider the ionization reactions for a conjugate acid-base pair, HA and A⁻:

HA (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + A^– (aq)

A^– (aq) + H₂O (l) ⇌ OH^– (aq) + HA (aq)

Adding these two chemical equations yields the equation for the autoionization for water:

HA (aq) + H₂O (l) + A^– (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + A^– (aq) + OH^– (aq) + HA (aq)

Simplifies to : 2 H₂O (l) ⇌ H₃O⁺ (aq) + OH^– (aq)

As discussed in Chapter 4, the K expression for any chemical equation that is derived by adding together two or more other equations is equal to the mathematical product of the individual K expressions. Multiplying the equilibrium constants together and canceling common terms, we see that:

   

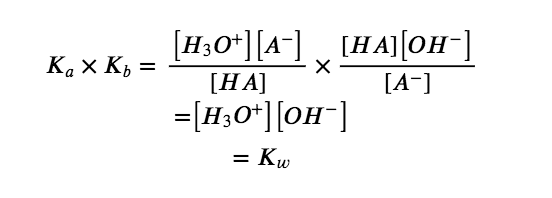
For example, the acid ionization constant of acetic acid (CH₃COOH) is 1.8 × 10⁻⁵, and the base ionization constant of its conjugate base, acetate ion (CH₃COO⁻), is 5.6 × 10⁻¹⁰. The product of these two constants is indeed equal to K_w:

K_a× K_b= (1.8×10^-5) × (5.6×10^-10)

= 1.0×10^-14 

=K_w

NOTE:

Make sure you fully understand the relationship between conjugate acids and bases: The conjugate base of an acid, HA, is what remains after it has donated a single proton, A–. The conjugate acid of a base, B, is what is produced after it has accepted a single proton, HB+. Note that in both cases, the two species in a conjugate acid-base pair differ by only one proton. This will be very important to remember and understand once we start discussing multiple Ka and Kb values for polyprotic acids – only the product of Ka and Kb between a conjugate acid-base pair will equal Kw.

The extent to which an acid, HA, donates protons to water molecules depends on the strength of the conjugate base, A⁻, of the acid. If A⁻ is a strong base (a good proton acceptor), any protons that are donated to water molecules to form hydronium ions are easily recaptured by A⁻ to regenerate HA. Thus there is relatively little A⁻ and H₃O⁺ in solution, and the acid, HA, is weak. If A⁻ is a weak base (poor proton acceptor), it remains in its deprotonated form, and the solution contains primarily A⁻ and H₃O⁺, and correspondingly the acid is strong. Hence, we derive the following important conclusion:

Strong acids form very weak conjugate bases, and strong bases form very weak conjugate acids.

This is illustrated in Figure 5.3.4: as the relative acid strength increases from right to left in the top bar, you can see that the strength of the corresponding conjugate bases decreases from right to left in the bottom bar.

Figure 5.3.4. This diagram shows the relative strengths of conjugate acid-base pairs, as indicated by their ionization constants in aqueous solution.

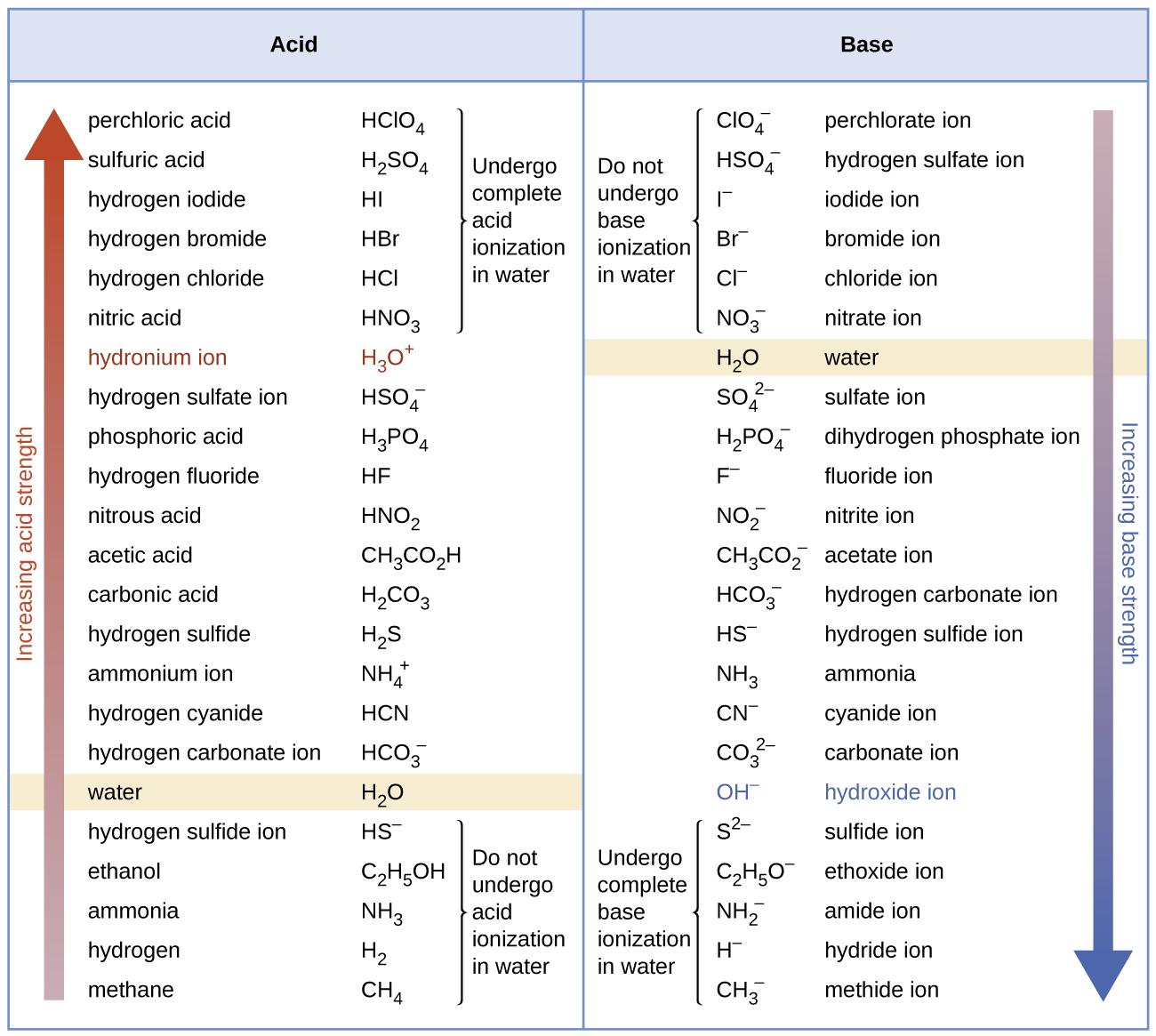
Figure 5.3.5. The chart shows the relative strengths of conjugate acid-base pairs.

Figure 5.3.5 also demonstrates this concept: the first six acids listed on the left are the most common strong acids. These acids are completely ionized in aqueous solution. The conjugate bases of these acids are weaker bases than water. When one of these acids dissolves in water, their protons are completely transferred to water, the stronger base.

Those acids that lie between the hydronium ion and water in Figure 5.3.5 form conjugate bases that can compete with water for possession of a proton. Both hydronium ions and unionized acid molecules are present in equilibrium in a solution of one of these acids. Compounds that are weaker acids than water (those found below water in the column of acids) in Figure 5.3.5 exhibit no observable acidic behavior when dissolved in water. Their conjugate bases are stronger than the hydroxide ion; if any conjugate base were formed, it would react with water to form the hydroxide ion.

The extent to which a base forms hydroxide ions in aqueous solution depends on the strength of the base relative to that of the hydroxide ion, as shown in the last column in Figure 5.3.5. A strong base, such as one of those lying below hydroxide ion, accepts protons from water to yield 100% of the conjugate acid and hydroxide ion. Those bases lying between water and hydroxide ion accept protons from water, but a mixture of the hydroxide ion and the base results. Bases that are weaker than water (those that lie above water in the column of bases) show no observable basic behavior in aqueous solution.

Example 5.3.2 –  the Product K_a × K_b = K_w

Using a K_b value of 1.8 × 10⁻¹¹ for the nitrite ion, NO₂⁻, calculate the K_a for its conjugate acid.

Solution

The conjugate acid of NO₂⁻ is HNO₂; K_a for HNO₂ can be calculated using the relationship

K_a×K_b = 1.0×10^-14 =K_w

Solving for K_a, we get:

K_a= K_w/K_b = 1.0×10^-14/1.8×10^-11 =5.6×10^-4

This answer matches the K_a for HNO₂ found in Table 5.3.1 and in

Appendix H.

Check Your Learning 5.3.2 –  the Product K_a × K_b = K_w

We can determine the relative acid strengths of NH₄⁺ and HCN by comparing their ionization constants. The ionization constant of HCN is given in Appendix H as 6.2 × 10⁻¹⁰. The ionization constant of NH₄⁺ is not listed, but the ionization constant of its conjugate base, NH₃, is listed as 1.8 × 10⁻⁵. Determine the ionization constant of NH₄⁺, and decide which is the stronger acid, HCN or NH₄⁺.

Answer

HCN is the slightly stronger acid (K_a for NH₄⁺ = 5.6 × 10⁻¹⁰).

Recall what we discussed earlier concerning the relationship between conjugate acids and bases: strong acids and bases will yield very weak conjugate bases and acids, respectively. We can use this fact to predict the direction of net change on an acid-base equilibrium reaction – the favoured direction of the reaction will be from the stronger to the weaker species of a conjugate pair. This relative strength can be assessed either qualitatively using a chart that shows the relative strengths of conjugate acid-base pairs (as in Figure 5.3.5) or quantitatively using K_a & K_b values, knowing that higher K_a and K_b values indicate stronger acids and bases, respectively. An example is shown below to illustrate this.

Example 5.3.3 – Predicting Products and Direction of Net Change – Acid-Base Equilibria

For the following acid-base reaction, predict the products and determine the preferred direction of change (i.e. the forward reaction, K > 1, or the reverse reaction, K < 1):

H₃PO₄ + HS^–

Solution

(a) H₃PO₄ is found much farther up in the chart (Figure 5.3.5) compared to HS^– in the acids column, meaning that it is the species that will preferentially donate its proton. Hence, it is our proton-donating acid and the bisulfide ion is our proton-accepting base. This gives us the following equilibrium reaction:

H₃PO₄ + HS^– ⇌ H₂PO₄^– + H₂S

Acid + Base ⇌ Conj. Base + Conj. Acid

To determine the preferred reaction direction, we must compare the relative strengths of the acid (in this case, H₃PO₄) and conjugate acid (H₂S) in this equilibrium: the stronger acid is the better proton donor, and thus will be more successful at donating its proton. As a result, the preferred equilibrium direction is always from the stronger acid to the weaker acid. Looking at the conjugate acid-base pairs in the chart, we find that H₃PO₄ is the relatively stronger acid compared to H₂S (likewise, HS^– is the relatively stronger base compared to H₂PO₄^–). Therefore, the reactants are the stronger species and hence the reaction preferentially proceeds to the right, i.e. towards products (K > 1).

We can verify our conclusion using K_a & K_b values as well (Appendices H & I). First, let’s look at the K_a values of the reactants to confirm the choice of products: the K_a values for H₃PO₄ and HS^– are 6.9 × 10^-3 and 1 × 10^-19, respectively. Of the two, phosphoric acid has a higher K_a value, so it is the better proton donor and hence will behave as the acid in this reaction. By consequence, that makes HS^– the base, the proton acceptor, and therefore the predicted products, H₂PO₄^– and H₂S, are correct.

Next, let’s use the K_a values of the acid and conjugate acid to confirm the predicted preferred reaction direction. Comparing these K_a values, we find that H₃PO₄ is indeed the better proton donor (K_a = 6.9 × 10^-3) than H₂S (K_a = 8.9 × 10^-8). Furthermore, if we calculate and compare K_b values between bases, HS^– is stronger (K_b = 1.1 × 10^-7) than H₂PO₄^– (K_b = 1.4 × 10^-12). Therefore, we confirm that the reactants are the stronger species and that the direction of net change is to the right.

Check Your Learning 5.3.3

Predict the products and determine the preferred direction of change for the following acid-base reaction:

HCO₃^– + HSO₃^–

Answer

The products are SO₃^2- and H₂CO₃. The direction of net change will be towards the left (i.e. the reactants HCO₃^– and HSO₃^–).

The Ionization of Weak Acids and Weak Bases

Many acids and bases are weak; that is, they do not ionize fully in aqueous solution. A solution of a weak acid in water is a mixture of the unionized acid, hydronium ion, and the conjugate base of the acid, with the unionized acid present in the greatest concentration. Thus, a weak acid increases the hydronium ion concentration in an aqueous solution (but not as much as the same amount of a strong acid).

Acetic acid, CH₃CO₂H, is a weak acid. When we add acetic acid to water, it ionizes to a small extent according to the equation:

CH₃CO₂H (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + CH₃CO₂^– (aq)

giving an equilibrium mixture with most of the acid present in the unionized (molecular) form. This equilibrium, like other equilibria, is dynamic; acetic acid molecules donate hydrogen ions to water molecules and form hydronium ions and acetate ions at the same rate that hydronium ions donate hydrogen ions to acetate ions to reform acetic acid molecules and water molecules. We can tell by measuring the pH of an aqueous solution of known concentration that only a fraction of the weak acid is ionized at any moment (Figure 5.3.4.). The remaining weak acid is present in the unionized form.

For acetic acid, at equilibrium:

   

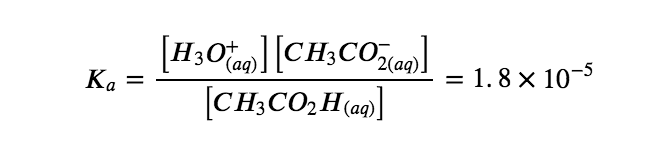
Figure 5.3.4.pH paper indicates that a 0.1 M solution of HCl (beaker on left) has a pH of 1. The acid is fully ionized and [H₃O⁺] = 0.1 M. A 0.1 M solution of CH₃CO₂H (beaker on right) is a pH of 3 ([H₃O⁺] = 0.001 M) because the weak acid CH₃CO₂H is only partially ionized. In this solution, [H₃O⁺] < [CH₃CO₂H]. (credit: modification of work by Sahar Atwa)

Table 5.3.1. Ionization Constants and pH (0.1 M) of Some Weak Acids.

The above table gives the ionization constants for several weak acids, including the pH for a 0.1 M solution of each acid; additional ionization constants can be found in Appendix H.

Looking at the pH of each 0.1 M solution of each weak acid, it’s important to appreciate the tremendous magnitude in the difference of acidity between various weak acids. For example, the K_a values for HCO₂H and CH₃COOH do not seem to be very different, and their pH values differ only by 0.5 units. However, we must appreciate that the K_a of HCO₂H is in fact 10 times larger than that of CH₃COOH, and that in terms of difference in acidity (difference in [H₃O⁺]), it is about 3 times more acidic. Now consider the difference between HCO₂H and HBrO – a pH difference of about 2.4 units. Doesn’t seem like much, but if we translate this in terms of acidity…a 0.1 M solution of HCO₂H is about 250 times more acidic than 0.1 M HBrO! Therefore, when you come across these seemingly small differences in pH, keep in mind that it is a logarithmic scale and their acidity actually differs significantly.

At equilibrium, a solution of a weak base in water is a mixture of the unionized base, the conjugate acid of the weak base, and hydroxide ion with the unionized base present in the greatest concentration. Thus, a weak base increases the hydroxide ion concentration in an aqueous solution (but not as much as the same amount of a strong base).

For example, a solution of the weak base trimethylamine, (CH₃)₃N, in water reacts according to the equation:

(CH₃)₃N (aq) + H₂O (l) ⇌ (CH₃)₃NH⁺ (aq) + OH^– (aq)

giving an equilibrium mixture with most of the base present as the unionized amine. This equilibrium is analogous to that described for weak acids.

We can confirm by measuring the pH of an aqueous solution of a weak base of known concentration that only a fraction of the base reacts with water (Figure 5.3.5.). The remaining weak base is present as the unreacted form. The equilibrium constant for the ionization of a weak base, K_b, is called the ionization constant of the weak base, and is equal to the reaction quotient when the reaction is at equilibrium. For trimethylamine, at equilibrium: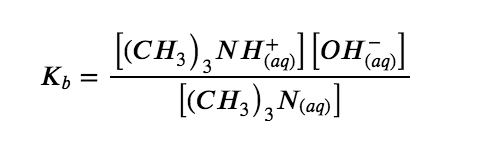  

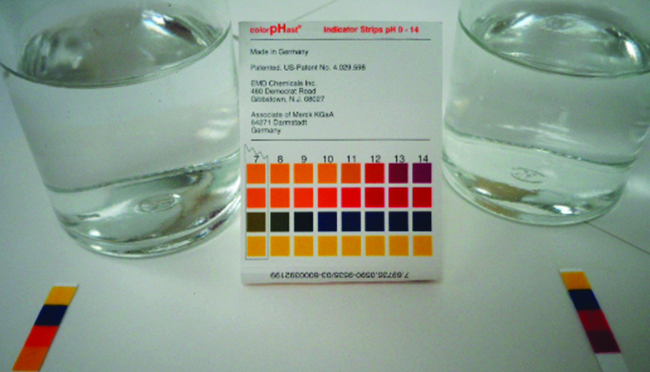
Figure 5.3.5.pH paper indicates that a 0.1 M solution of NH₃ (left) is weakly basic. The solution has a pOH of 3 ([OH⁻] = 0.001 M) because the weak base NH₃ only partially reacts with water. A 0.1 M solution of NaOH (right) has a pOH of 1 because NaOH is a strong base. (credit: modification of work by Sahar Atwa)

The ionization constants of several weak bases are given in table below and in Appendix I.

Ionization Constants of Some Weak Bases
Ionization Reaction	Kb at 25 °C
(CH3)2NH + H2O ⇌ (CH3)2NH2+ + OH–	5.9 × 10−4
CH3NH2 + H2O ⇌ CH3NH3+ + OH–	4.4 × 10−4
(CH3)3N + H2O ⇌ (CH3)3NH+ + OH–	6.3 × 10−5
NH3 + H2O ⇌ NH4+ + OH–	1.8 × 10−5
C6H5NH2 + H2O ⇌ C6N5NH3+ + OH–	4.3 × 10−10

Example 5.3.4 – Determination of K_a from Equilibrium Concentrations

Acetic acid is the principal ingredient in vinegar (Figure 5.3.6.) resulting in its sour taste. At equilibrium, a solution contains [CH₃CO₂H] = 0.0787 M and [H₃O⁺] = [CH₃CO₂⁻] = 0.00118 M. What is the value of K_a for acetic acid?

Figure 5.3.6. Vinegar is a solution of acetic acid, a weak acid. (credit: modification of work by “HomeSpot HQ”/Flickr)

Solution

We are asked to calculate an equilibrium constant from equilibrium concentrations. At equilibrium, the value of the equilibrium constant is equal to the reaction quotient for the reaction:

CH₃CO₂H (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + CH₃CO₂^– (aq)

   

Check Your Learning 5.3.4 – Determination of K_a from Equilibrium Concentrations

What is the equilibrium constant for the ionization of the HSO₄⁻ ion, the weak acid used in some household cleansers:

HSO₄^– (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + SO₄^2- (aq)

In one mixture of NaHSO₄ and Na₂SO₄ at equilibrium, [H₃O⁺] = 0.027 M; [HSO₄⁻] = 0.29 M; and [SO₄²⁻] = 0.13 M.

Answer

K_a for HSO₄⁻ = 1.2 × 10⁻²

Example 5.3.5 – Determination of K_b from Equilibrium Concentrations

Caffeine, C₈H₁₀N₄O₂ is a weak base. What is the value of K_b for caffeine if a solution at equilibrium has [C₈H₁₀N₄O₂] = 0.050 M, [C₈H₁₀N₄O₂H⁺] = 5.0 × 10⁻³ M, and [OH⁻] = 2.5 × 10⁻³ M?

Solution

At equilibrium, the value of the equilibrium constant is equal to the reaction quotient for the reaction:

C₈H₁₀N₄O₂ (aq) + H₂O (l) ⇌ C₈H₁₀N₄O₂⁺ (aq) + OH^– (aq)

   

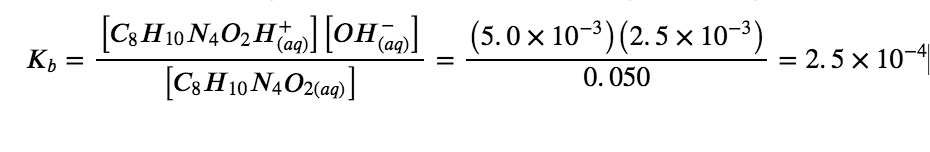
Check Your Learning 5.3.5 – Determination of K_b from Equilibrium Concentrations

What is the equilibrium constant for the ionization of the HPO₄²⁻ ion, a weak base:

HPO₄^2– (aq) + H₂O (l) ⇌ H₂PO₄^– (aq) + OH^– (aq)

in a solution containing a mixture of NaH₂PO₄ and Na₂HPO₄ at equilibrium, [OH⁻] = 1.3 × 10⁻⁶ M; [H₂PO₄⁻]=0.042 M; and [HPO₄²⁻]=0.341 M.

Answer

K_b for HPO₄²⁻ = 1.6 × 10⁻⁷

Example 5.3.6 – Determination of K_a or K_b from pH

The pH of a 0.0516 M solution of nitrous acid, HNO₂, is 2.34. What is its K_a?

HNO₂ (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + NO₂^– (aq)

Solution

We determine an equilibrium constant starting with the initial concentrations of HNO₂, H₃O⁺, and NO₂⁻ as well as one of the final concentrations, the concentration of hydronium ion at equilibrium. (Remember that pH is simply another way to express the hydronium ion concentration). Notice how this type of problem falls under one of the two types of chemical equilibrium problems covered in the previous unit (4.3 – Solving Equilibrium Problems) – we’re calculating an equilibrium constant given that we know/determine the concentration of reactants and products at equilibrium.

We can solve this problem with the following steps in which x is a change in concentration of a species in the reaction:

To get the various values in the ICE (Initial, Change, Equilibrium) table, we first calculate [H₃O⁺], the equilibrium concentration of H₃O⁺, from the pH:

 [H₃O⁺] = 10^-2.34 = 0.0046 M

The change in concentration of H₃O⁺, X_[H3O+], is the difference between the equilibrium concentration of H₃O⁺, which we determined from the pH, and the initial concentration, [H₃O⁺]_i. The initial concentration of H₃O⁺ is its concentration in pure water, 1 x 10^–7 M, which is so much less than the final concentration that we can approximate it as zero (~0) in order to simplify our calculations.

The change in concentration of NO₂⁻ is equal to the change in concentration of [H₃O⁺]: the stoichiometry of the reaction dictates that for each 1 mol of H₃O⁺ that forms, 1 mol of NO₂⁻ forms. The equilibrium concentration of HNO₂ is equal to its initial concentration plus the change in its concentration.

Now we can fill in the ICE table with the concentrations at equilibrium, as

shown here:

HNO₂ + H₂O⇌ H₃O⁺ + NO₂^–

Finally, we calculate the value of the equilibrium constant using the data in the table:

 

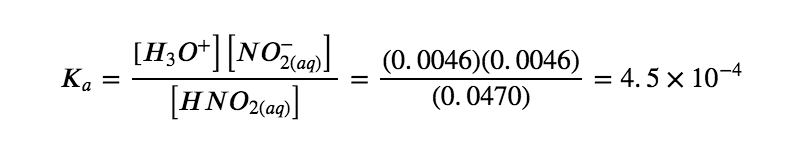
Check Your Learning 5.3.6 – Determination of K_a or K_b from pH

The pH of a solution of household ammonia, a 0.950 M solution of NH₃, is 11.612. What is K_b for NH₃.

Answer

K_b = 1.8 × 10⁻⁵

Example 5.3.7 – Equilibrium Concentrations in a Solution of a Weak Acid

Formic acid, HCO₂H, is the irritant that causes the body’s reaction to ant stings (Figure 5.3.7).

Figure 5.3.7. The pain of an ant’s sting is caused by formic acid. (credit: John Tann)

What is the concentration of hydronium ion and the pH in a 0.534 M solution of formic acid?

HCO₂H (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + HCO₂^– (aq)          K_a = 1.8 x 10^-4

Solution

Determine x and equilibrium concentrations. The equilibrium expression is:

HCO₂H (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + HCO₂^– (aq)

The table shows initial concentrations (concentrations before the acid ionizes), changes in concentration, and equilibrium concentrations follows (the data given in the problem appear in colour):

HCO₂H + H₂O⇌ H₃O⁺ + NO₂^–

Solve for x and the equilibrium concentrations. At equilibrium: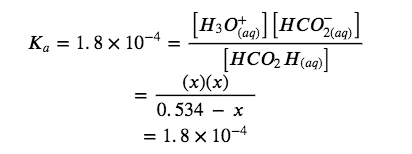

Now solve for x. Because the initial concentration of acid is reasonably large and K_a is very small, we make the assumption that x << 0.534, which allows us to simplify the denominator term as (0.534 − x) = 0.534. This gives:

Solve for x as follows:

 

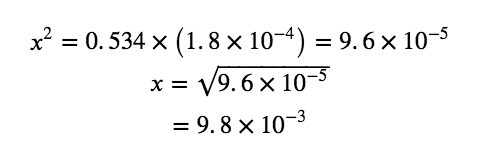
To check the assumption that x is small compared to 0.534, we

calculate:

(x/0.534)(100%)=1.8%

x is less than 5% of the initial concentration and so the assumption is

valid.

We find the equilibrium concentration of hydronium ion in this formic acid solution from its initial concentration and the change in that concentration as indicated in the last line of the table:

[H₃O⁺]= ∼0+x = 0+ 9.8×10^-3M

=9.8×10^-3M

The pH of the solution is thus:

pH=-log(9.8×10^-3)=2.01

Check Your Learning 5.3.7 – Equilibrium Concentrations in a Solution of a Weak Acid

Only a small fraction of a weak acid ionizes in aqueous solution. What is the percent ionization of acetic acid in a 0.100 M solution of acetic acid, CH₃CO₂H?

CH₃CO₂H (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + CH₃CO₂^– (aq)        K_a = 1.8 x 10^-5

(Hint: Determine [CH₃CO₂⁻] at equilibrium.) Recall that the percent ionization is the fraction of acetic acid that is ionized × 100, or:

Answer

Percent Ionization = 1.3%

The following example shows that the concentration of products produced by the ionization of a weak base can be determined by the same series of steps used with a weak acid.

Example 5.3.8 – Equilibrium Concentrations in a Solution of a Weak Base

Find the concentration of hydroxide ion in a 0.25 M solution of trimethylamine, a weak base:

(CH₃)₃N (aq) + H₂O (l) ⇌ (CH₃)₃NH⁺ (aq) + OH^– (aq)K_b = 6.3 x 10^-5

Solution

This problem requires that we calculate an equilibrium concentration by determining concentration changes as the ionization of a base goes to equilibrium. The solution is approached in the same way as that for the ionization of formic acid in the previous example. The reactants and products will be different and the numbers will be different, but the logic will be the same:

Determine x and equilibrium concentrations. The table shows the changes and concentrations:

(CH₃)₃N + H₂O⇌ (CH₃)₃NH⁺ + OH^–

Solve for x and the equilibrium concentrations. At equilibrium:

 

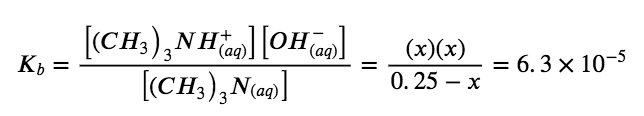
If we assume that x is small relative to 0.25, then we can replace (0.25 − x) in the preceding equation with 0.25. Solving the simplified equation gives:

x=4.0×10^-3

This change is less than 5% of the initial concentration (0.25 M), so the assumption is justified.

Recall that, for this computation, x is equal to the equilibrium concentration of hydroxide ion in the solution (see earlier tabulation):

[OH-]=∼0+x, x=4.0×10^-3 M

[OH-]=4.0×10^-3

Then calculate pOH as follows:

pOH=-log(4.0×10^-3)=2.40

Using the relation introduced in the previous section of this chapter:

pH+pOH=pK_w=14.00

This allows us to determine the pH:

pH=14.00-pOH=14.00-2.40=11.60

Check the work. A check of our arithmetic shows that K_b = 6.3 × 10⁻⁵.

Check Your Learning 5.3.8 – Equilibrium Concentrations in a Solution of a Weak

Base

(a) Show that the calculation in Step 2 of this example gives an x of 4.0 × 10⁻³ and the calculation in Step 3 shows K_b = 6.3 ×10⁻⁵.

(b) Find the concentration of hydroxide ion in a 0.0325 M solution of ammonia, a weak base with a K_b of 1.76 × 10⁻⁵. Calculate the percent ionization of ammonia, the fraction ionized × 100%, or:

([NH₄⁺]_eq/[NH₃]_i)×100%

Answer

7.56 × 10⁻⁴ M, 2.33%

Some weak acids and weak bases ionize to such an extent that the simplifying assumption that “x is small relative to the initial concentration of the acid or base” is inappropriate. As we solve for the equilibrium concentrations in such cases, we will see that we cannot neglect the change in the initial concentration of the acid or base, and we must solve the equilibrium equations by using the quadratic equation.

Example 5.3.9 – Equilibrium Concentrations in a Solution of a Weak Acid

Sodium bisulfate, NaHSO₄, is used in some household cleansers because it contains the HSO₄⁻ ion, a weak acid. What is the pH of a 0.50 M solution of HSO₄⁻?

HSO₄^– (aq) + H₂O (l) ⇌ H₃O⁺ (aq) + SO₄^2- (aq)K_a = 1.2 x 10^-2

Solution

One question that may come up is why we aren’t considering the case of HSO₄^– acting as a proton acceptor since it is an amphiprotic species. There are 2 reasons:

1) HSO₄^– is relatively much more acidic than water (Figure 5.3.5), so in this acid-base reaction, it will be most inclined to be the proton donor, and

2) if HSO₄^– was the proton acceptor (and H₂O was the proton donor), we would get H₂SO₄ and OH^–. These are very strong acid and base products, so ultimately, the reaction would proceed to completion to the left; in other words, the forward reaction would essentially not proceed at all, which is why we can disregard this possibility.

We need to determine the equilibrium concentration of the hydronium ion that results from the ionization of HSO₄⁻ so that we can use [H₃O⁺] to determine the pH. As in the previous examples, we can approach the solution by the following steps:

Determine x and equilibrium concentrations. This table shows the changes

and concentrations:

HSO₄^– + H₂O⇌ H₃O⁺ + SO₄^2-

Solve for x and the concentrations. As we begin solving for x, we will find this is more complicated than in previous examples. As we discuss these complications we should not lose track of the fact that it is still the purpose of this step to determine the value of x.

At equilibrium:

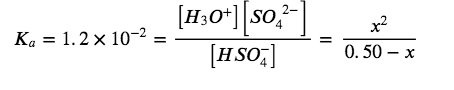
If we assume that x is small and approximate (0.50 − x) as 0.50, we find:

x=7.7×10^-2

When we check the assumption, we calculate:

 

The value of x is not less than 5% of 0.50, so the assumption is not valid. We need the quadratic formula to find x.

The equation:

K_a=1.2×10^-2=x²/(0.50-x)

Gives

6.0×10^-3 – 1.2×10^-2x=x²

Or

x²+ 1.2×10^-2x -6.0×10^-3=0

This equation can be solved using the quadratic formula. For an equation of the form

ax²+bx+c=0

x is given by the equation:

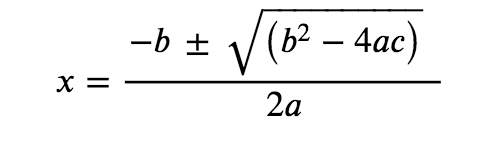
In this problem, a = 1, b = 1.2 × 10⁻³, and c = −6.0 × 10⁻³.

Solving for x gives a negative root and a positive root. Since the negative root cannot possibly be correct (a concentration cannot be negative), we will continue our solution using the positive root:

x= 7.2×10^-2

Now determine the hydronium ion concentration and the pH:

[H₃O⁺]=∼0+x, x=7.2×10^-2 M

[H₃O⁺]=7.2×10^-2 M

The pH of this solution is:

pH=-log[H₃O⁺]=-log(7.2×10^-2)=1.14

Check Your Learning 5.3.9 – Equilibrium Concentrations in a Solution of a

Weak Acid

(a) Show that the quadratic formula gives x = 7.2 × 10⁻².

(b) Calculate the pH in a 0.010 M solution of caffeine, a weak base:

C₈H₁₀N₄O₂ (aq) + H₂O (l) ⇌ C₈H₁₀N₄O₂H⁺ (aq) + OH^– (aq)K_b = 2.5 x 10^-4

(Hint: It will be necessary to convert [OH⁻] to [H₃O⁺] or pOH to pH toward the end of the calculation.)

Answer

pH = 11.16

The Relative Strengths of Strong Acids and Bases

Strong acids, such as HCl, HBr, and HI, all exhibit the same strength in water. The water molecule is such a better proton acceptor when compared to the conjugate bases Cl⁻, Br⁻, and I⁻ that ionization of these strong acids is essentially complete in aqueous solutions. In solvents less basic than water, we find HCl, HBr, and HI differ markedly in their tendency to give up a proton to the solvent. For example, when dissolved in ethanol (a weaker base than water), the extent of ionization increases in the order HCl < HBr < HI, and so HI is demonstrated to be the strongest of these acids. The inability to discern differences in strength among strong acids dissolved in water is known as the leveling effect of water.

Water also exerts a leveling effect on the strengths of strong bases. For example, the oxide ion, O²⁻, and the amide ion, NH₂⁻, are such strong bases that they react completely with water:

O^2– (aq) + H₂O (l) → OH^– (aq) + OH^– (aq)

NH₂^– (aq) + H₂O (l) → NH₃ (aq) + OH^– (aq)

Thus, O²⁻ and NH₂⁻ appear to have the same base strength in water; they both give a 100% yield of hydroxide ion. Consequently, this signifies that O^2- and NH₂^– as species do not exist in aqueous solutions.

Effect of Molecular Structure on Acid-Base Strength

NOTE: This topic is briefly covered to understand acid-base strength due to molecular structure. However, this is emphasized to a much greater extent and discussed in greater detail in the Winter semester course CHM1321: Organic Chemistry I.

In the absence of any leveling effect, the acid strength of binary compounds of hydrogen with nonmetals (A) increases as the H-A bond strength decreases down a group in the periodic table. For group 17, the order of increasing acidity is HF < HCl < HBr < HI. Likewise, for group 16, the order of increasing acid strength is H₂O < H₂S < H₂Se < H₂Te.

Across a row in the periodic table, the acid strength of binary hydrogen compounds increases with increasing electronegativity of the nonmetal atom because the polarity of the H-A bond increases (note: if you are unfamiliar with the concept of electronegativity, it is discussed in Section 9.1). Thus, the order of increasing acidity (for removal of one proton) across the second row is CH₄ < NH₃ < H₂O < HF; across the third row, it is SiH₄ < PH₃ < H₂S < HCl (see Figure 5.3.8).

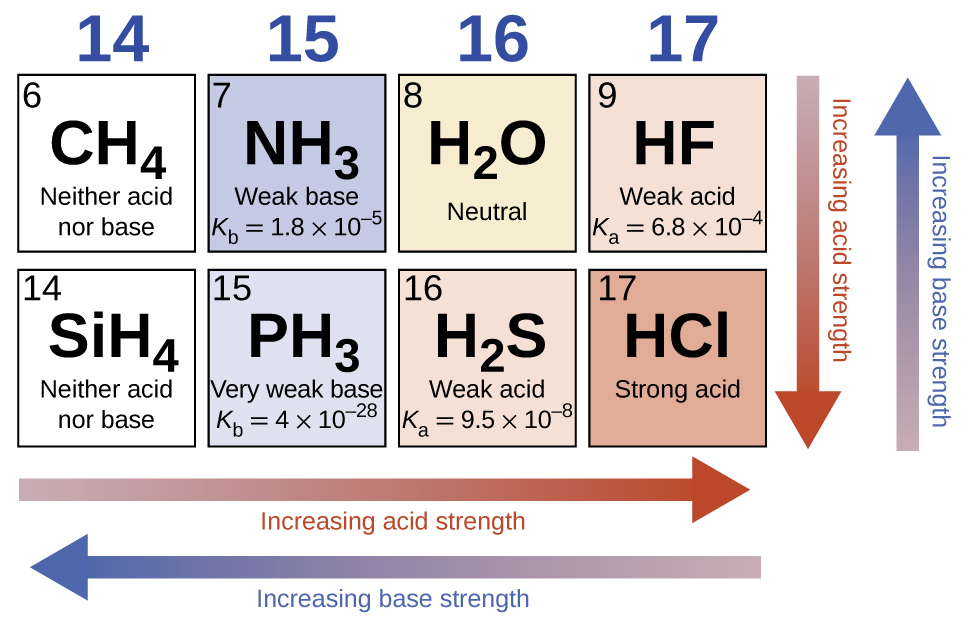
Figure 5.3.8.As you move from left to right and down the periodic table, the acid strength increases. As you move from right to left and up, the base strength increases.

Compounds containing oxygen and one or more hydroxyl (OH) groups can be acidic, basic, or amphoteric, depending on the position in the periodic table of the central atom E, the atom bonded to the hydroxyl group. Such compounds have the general formula O_nE(OH)_m, and include sulfuric acid, O₂S(OH)₂, sulfurous acid, OS(OH)₂, nitric acid, O₂NOH, perchloric acid, O₃ClOH, aluminum hydroxide, Al(OH)₃, calcium hydroxide, Ca(OH)₂, and potassium hydroxide, KOH:

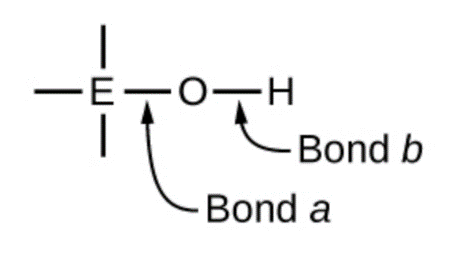
Atom electronegativity and its relationship to bond character is discussed in detail in Section 9.1, but briefly: electronegativity is a measure of the ability of an atom to attract bonding electrons towards its nucleus. The nature of the chemical bond between two atoms (X–Y) is directly correlated to the difference in electronegativity between the two atoms, i.e. ∆EN_XY = |EN_X – EN_Y|. A low value of ∆EN_XY results in a chemical bond that is mostly covalent – the electrons are being equally shared by both atoms. A high value of ∆EN_XY results in a chemical bond that is mostly ionic in character – the electron density is not equally distributed and cleavage of the bond will likely create one cation and one anion.

Referring back to the scheme above, the O atom has a high EN value. If the central atom, E, has a low electronegativity, then ∆EN_EO is large and the central atom tends to form a bond with greater ionic character with the oxygen atom. Consequently, bond a between the element and oxygen is more readily broken than bond b between oxygen and hydrogen. Hence bond a is ionic, hydroxide ions are released to the solution, and the material behaves as a base—this is the case with Ca(OH)₂ and KOH. Lower electronegativity is characteristic of the more metallic elements; hence, the metallic elements form ionic hydroxides that are by definition basic compounds.

If, on the other hand, the E atom has a relatively high electronegativity, ∆EN_EO is low, and the E atom shares the bonding electrons equally with the oxygen atom, making bond a relatively strongly covalent. Comparatively, the oxygen-hydrogen bond, bond b, has greater ionic character and is much more polar. As a consequence, the O-H bond is more readily broken and releases hydrogen ions to the solution, so the material behaves as an acid. High electronegativities are characteristic of the more nonmetallic elements. Thus, nonmetallic elements form covalent compounds containing acidic −OH groups, known as oxoacids.

Increasing the oxidation state of the central atom E also increases the acidity of an oxyacid because this increases the attraction of E for the electrons it shares with oxygen. This polarization of electron density weakens the O-H bond, resulting in easier ionization. For example, sulfuric acid, H₂SO₄, or O₂S(OH)₂ (with a sulfur oxidation number of +6), is more acidic than sulfurous acid, H₂SO₃, or OS(OH)₂ (with a sulfur oxidation number of +4). Likewise nitric acid, HNO₃, or O₂NOH (N oxidation number = +5), is more acidic than nitrous acid, HNO₂, or ONOH (N oxidation number = +3). In each of these pairs, the oxidation number of the central atom is larger for the stronger acid (Figure 5.3.9.).

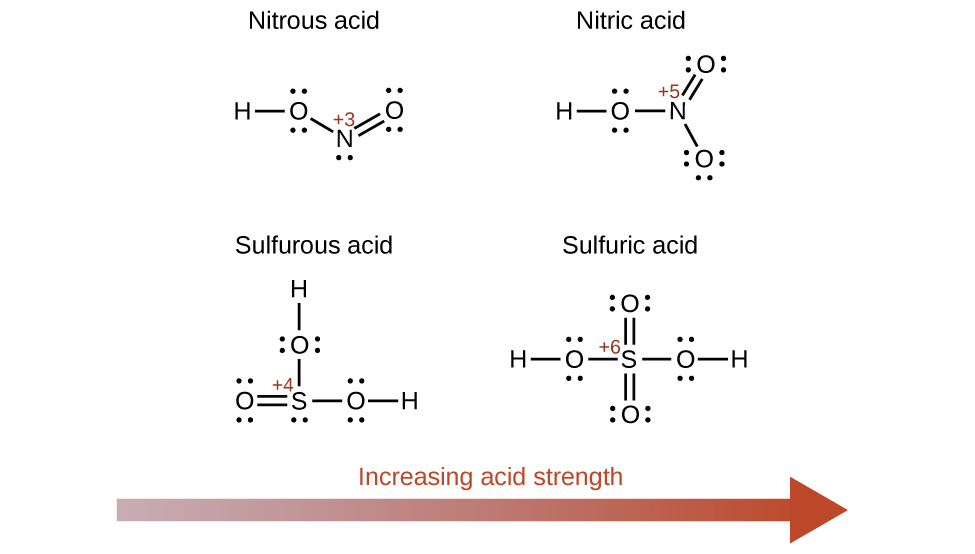
Figure 5.3.9.As the oxidation number of the central atom E increases, the acidity also increases.

Hydroxy compounds of elements with intermediate electronegativities and relatively high oxidation numbers (for example, elements near the diagonal line separating the metals from the nonmetals in the periodic table) are usually amphoteric. This means that the hydroxy compounds act as acids when they react with strong bases and as bases when they react with strong acids. The amphoterism of aluminum hydroxide, which commonly exists as the hydrate Al(H₂O)₃(OH)₃, is reflected in its solubility in both strong acids and strong bases. In strong bases, the relatively insoluble hydrated aluminum hydroxide, Al(H₂O)₃(OH)₃, is converted into the soluble ion, [Al(H₂O)₂(OH)₄]⁻, by reaction with hydroxide ion:

Al(H₂O)₃(OH)₃ (aq) + OH^– (aq) ⇌ H₂O (l) + [Al(H₂O)₂(OH)₄]^– (aq)

In this reaction, a proton is transferred from one of the aluminum-bound H₂O molecules to a hydroxide ion in solution. The Al(H₂O)₃(OH)₃ compound thus acts as an acid under these conditions. On the other hand, when dissolved in strong acids, it is converted to the soluble ion [Al(H₂O)₆]³⁺ by reaction with hydronium ion:

3H₃O⁺ (aq) + Al(H₂O)₃(OH)₃ (aq) ⇌ Al(H₂O)₆³⁺ (aq) + 3H₂O (l)

In this case, protons are transferred from hydronium ions in solution to Al(H₂O)₃(OH)₃, and the compound functions as a base.

Questions

★ Questions

1. Explain why the neutralization reaction of a strong acid and a weak base gives a weakly acidic solution.

2. Use this list of important industrial compounds (and Figure 5.3.3.) to answer the following questions regarding: CaO, Ca(OH)₂, CH₃CO₂H, CO₂, HCl, H₂CO₃, HF, HNO₂, HNO₃, H₃PO₄, H₂SO₄, NH₃, NaOH, Na₂CO₃. Identify the strong Brønsted-Lowry acids and strong Brønsted-Lowry bases.

(a) List those compounds in (a) that can behave as Brønsted-Lowry acids with strengths lying between those of H₃O⁺ and H₂O.

(b) List those compounds in (a) that can behave as Brønsted-Lowry bases with strengths lying between those of H₂O and OH⁻.

(c) The odor of vinegar is due to the presence of acetic acid, CH₃CO₂H, a weak acid. List, in order of descending concentration, all of the ionic and molecular species present in a 1 M aqueous solution of this acid.

3. Household ammonia is a solution of the weak base NH₃ in water. List, in order of descending concentration, all of the ionic and molecular species present in a 1 M aqueous solution of this base.

4. Explain why the ionization constant, Ka, for H₂SO₄ is larger than the ionization constant for H₂SO₃.

5. Gastric juice, the digestive fluid produced in the stomach, contains hydrochloric acid, HCl. Milk of Magnesia, a suspension of solid Mg(OH)₂ in an aqueous medium, is sometimes used to neutralize excess stomach acid. Write a complete balanced equation for the neutralization reaction, and identify the conjugate acid-base pairs.

6. Nitric acid reacts with insoluble copper(II) oxide to form soluble copper(II) nitrate, Cu(NO₃)₂, a compound that has been used to prevent the growth of algae in swimming pools. Write the balanced chemical equation for the reaction of an aqueous solution of HNO₃ with CuO.

7. What is the ionization constant at 25 °C for the weak acid CH₃NH₃⁺, the conjugate acid of the weak base CH₃NH₂, K_b= 4.4 × 10⁻¹¹?

8. Which is the stronger acid, NH₄⁺ or HBrO?

9. Which is the stronger base, (CH₃)₃N or H₂BO₃⁻?

10. Predict which compound in each of the following pairs of compounds is more acidic and explain your reasoning for each.

(a) HSO₄^– or HSeO₄^–

(b) NH₃ or H₂O

(c) PH₃ or HI

(d) NH₃ or PH₃

(e) H₂S or HBr

11. Rank the compounds in each of the following groups in order of increasing acidity or basicity, as indicated, and explain the order you assign.

(a) acidity: HCl, HBr, HI

(b) basicity: H₂O, OH⁻, H⁻, Cl⁻

(c) basicity: Mg(OH)₂, Si(OH)₄, ClO₃(OH) (Hint: Formula could also be written as HClO₄).

(d) acidity: HF, H₂O, NH₃, CH₄

12. Both HF and HCN ionize in water to a limited extent. Which of the conjugate bases, F⁻ or CN⁻, is the stronger base? See the ionization constants of weak acids to solve this problem.

13. The active ingredient formed by aspirin in the body is salicylic acid, C₆H₄OH(CO₂H). The carboxyl group (−CO₂H) acts as a weak acid. The phenol group (an OH group bonded to an aromatic ring) also acts as an acid but a much weaker acid. List, in order of descending concentration, all of the ionic and molecular species present in a 0.001 M aqueous solution of C₆H₄OH(CO₂H).

14. What do we represent when we write:

CH₃CO₂H (aq) + H₂O (l) ⇌ H₃O ⁺ (aq) + CH₃CO₂ ^– (aq)

15. Explain why equilibrium calculations are not necessary to determine ionic concentrations in solutions of certain strong electrolytes such as NaOH and HCl. Under what conditions are equilibrium calculations necessary as part of the determination of the concentrations of all ions of some other strong electrolytes in solution?

16. Are the concentrations of hydronium ion and hydroxide ion in a solution of an acid or a base in water directly proportional or inversely proportional? Explain your answer.

17. What two common assumptions can simplify calculation of equilibrium concentrations in a solution of a weak acid?

18. What two common assumptions can simplify calculation of equilibrium concentrations in a solution of a weak base?

19. Which of the following will increase the percent of NH₃ that is converted to the ammonium ion in water (Hint: Use LeChâtelier’s principle.)?

(a) addition of NaOH

(b) addition of HCl

(c) addition of NH₄Cl

20. Which of the following will increase the percent of HF that is converted to the fluoride ion in water?

(a) addition of NaOH

(b) addition of HCl

(c) addition of NaF

21. What is the effect on the concentrations of NO₂^–, HNO₂, and OH− when the following are added to a solution of KNO₂ in water:

(a) HCl

(b) HNO₂

(c) NaOH

(d) NaCl

(e) KNO

22. The equation for the equilibrium is:

NO₂ ^– (aq) + H₂O (l) ⇌ HNO₂ (aq) + OH ^– (aq)

Why is the hydronium ion concentration in a solution that is 0.10 M in HCl and 0.10 M in HCOOH determined by the concentration of HCl?

23. From the equilibrium concentrations given, calculate K_a for each of the weak acids and K_b for each of the weak bases.

 

 

 

 

★★ Questions

24. Determine K_b for the nitrite ion, NO₂⁻. In a 0.10 M solution this base is 0.0015% ionized.

25. Determine K_a for hydrogen sulfate ion, HSO₄⁻. In a 0.10 M solution the acid is 29% ionized.

26. Calculate the ionization constant for each of the following acids or bases from the ionization constant of its conjugate base or conjugate acid:

(a) HTe^– (as a base)

(b) (CH₃)₃NH⁺

(c) HAsO₄^3- (as a base)

(d) HO₂^– (as a base)

(e) C₆H₅NH₃⁺

(f) HSO₃^– (as a base)

27. For which of the following solutions must we consider the ionization of water when calculating the pH or pOH?

(a) 3 × 10⁻⁸ M HNO₃

(b) 0.10 g HCl in 1.0 L of solution

(c) 0.00080 g NaOH in 0.50 L of solution

(d) 1 × 10⁻⁷ M Ca(OH)₂

(e) 0.0245 M KNO₃

28. Calculate the equilibrium concentration of the unionized acids and all ions in a solution that is 0.134 M in HNO₂ and 0.120 M in HBrO.

29. Calculate the equilibrium concentration of the unionized bases and all ions in a solution that is 0.115 M in NH₃ and 0.100 M in C₆H₅NH₂.

30. Propionic acid, C₂H₅CO₂H (K_a = 1.34 × 10⁻⁵), is used in the manufacture of calcium propionate, a food preservative. What is the hydronium ion concentration in a 0.698 M solution of C₂H₅CO₂H?

31. The pH of a 0.15 M solution of HSO₄⁻ is 1.43. Determine K_a for HSO₄⁻ from these data.

32. The pH of a solution of household ammonia, a 0.950 M solution of NH₃, is 11.612. Determine K_b for NH₃ from these data.