4.1 – Introduction to Chemical Equilibrium

A chemical reaction is usually written in a way that suggests it proceeds in one direction, the direction in which we read, but all chemical reactions are reversible, and both the forward and reverse reaction occur to one degree or another depending on conditions – this is the notion of chemical equilibrium which we will discuss here in this chapter.

Dynamic Equilibrium

In a chemical equilibrium, the forward and reverse reactions occur at equal rates, and the concentrations of products and reactants remain constant. If we run a reaction in a closed system so that the products cannot escape, we often find the reaction does not give a 100% yield of products. Instead, some reactants remain after the concentrations stop changing. At this point, when there is no further change in concentrations of reactants and products, we say the reaction is at equilibrium. A mixture of reactants and products is found at equilibrium.

For example, when we place a sample of dinitrogen tetroxide (N₂O₄, a colorless gas) in a glass tube, it forms nitrogen dioxide (NO₂, a brown gas) by the following reaction:

N₂O₄ (g)  ⇌  2 NO₂ (g)

The color becomes darker as N₂O₄ is converted to NO₂. When the system reaches equilibrium, both N₂O₄ and NO₂ are present (Figure 4.1.1).

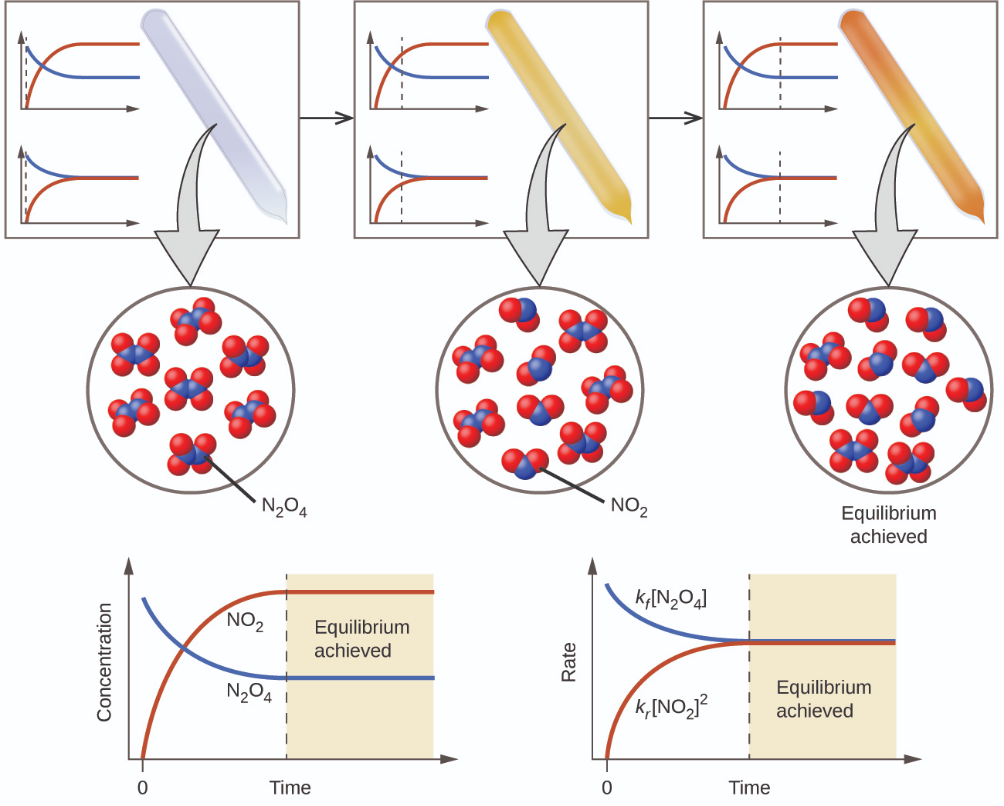
Figure 4.1.1. A mixture of NO₂ and N₂O₄ moves toward equilibrium. Colorless N₂O₄ reacts to form brown NO₂. As the reaction proceeds toward equilibrium, the color of the mixture darkens due to the increasing concentration of NO₂. (Chem Libre, From: https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_General_Chemistry_(Petrucci_et_al.)/15%3A_Principles_of_Chemical_Equilibrium/15.1%3A_Dynamic_Equilibrium, Creative Commons)

The formation of NO₂ from N₂O₄ is a reversible reaction, which is identified by the equilibrium arrows (⇌). All reactions are reversible, but many reactions, for all practical purposes, proceed in the forward direction until the reactants are exhausted and will reverse only under certain conditions. Such reactions are often depicted with a one-way arrow from reactants to products. Many other reactions, such as the formation of NO₂ from N₂O₄, are reversible under more easily obtainable conditions and, therefore, are named as such. In a reversible reaction, the reactants can combine to form products and the products can react to form the reactants. Thus, not only can N₂O₄ decompose to form NO₂, but the NO₂ produced can react to form N₂O₄. As soon as the forward reaction produces any NO₂, the reverse reaction begins and NO₂ starts to react to form N₂O₄. At equilibrium, the concentrations of N₂O₄ and NO₂ no longer change because the rate of formation of NO₂ is exactly equal to the rate of consumption of NO₂, and the rate of formation of N₂O₄ is exactly equal to the rate of consumption of N₂O₄. Hence we get to a key idea: Chemical equilibrium is a dynamic process. For example, if two jugglers are each tossing clubs at the other at the same rate at which each receives clubs from the other, the numbers of clubs each will have at any point in time will remain roughly constant, yet there is always a flux back and forth between them (Figure 4.1.2).

Figure 4.1.2. These jugglers provide an illustration of dynamic equilibrium. Each throws clubs to the other at the same rate at which he receives clubs from that person. Because clubs are thrown continuously in both directions, the number of clubs moving in each direction is constant, and the number of clubs each juggler has at a given time remains (roughly) constant.

In a chemical equilibrium, the forward and reverse reactions do not stop, rather they continue to occur at the same rate, leading to constant concentrations of the reactants and the products. Plots showing how the reaction rates and concentrations change with respect to time are shown in Figure 4.1.1.

We can detect a state of equilibrium because the concentrations of reactants and products do not appear to change. However, it is important that we verify that the absence of change is due to equilibrium and not to a reaction rate that is so slow that changes in concentration are difficult to detect.

We use a double arrow when writing an equation for a reversible reaction. Such a reaction may or may not be at equilibrium. For example, Figure 4.1.1 shows the reaction:

When we wish to speak about one particular component of a reversible reaction, we use a single arrow. For example, in the equilibrium shown in Figure 4.1.1, the rate of the forward reaction with rate constant k_f

We’ll talk more about rate constants in Chapter 7: Chemical Kinetics; for now, all you need to know is that each rate constant is unique to a particular reaction that helps mathematically define its rate of reaction.

The equilibrium between N₂O₄ and NO₂ consists of a chemical equilibrium – one which involves two or more substances through a chemical reaction. However, an equilibrium consisting of a single substance, known as a physical equilibrium, can be established for a physical change—like a liquid to gas transition—as well as for a chemical reaction. Let us consider the evaporation of bromine as a second example of a system at equilibrium.

Br₂ (l)   ⇌   Br₂ (g)

Figure 4.1.4 shows a sample of liquid bromine at equilibrium with bromine vapour in a closed container. When we pour liquid bromine into an empty bottle in which there is no bromine vapour, some liquid evaporates, the amount of liquid decreases, and the amount of vapour increases. If we cap the bottle so no vapour escapes, the amount of liquid and vapour will eventually stop changing and an equilibrium between the liquid and the vapour will be established. If the bottle were not capped, the bromine vapour would escape and no equilibrium would be reached.

Figure 4.1.4. An equilibrium is pictured between liquid bromine, Br₂ (l), the dark liquid, and bromine vapour, Br₂ (g), the reddish-brown gas. Because the container is sealed, bromine vapour cannot escape and equilibrium is maintained. (credit: http://images-of-elements.com/bromine.php)

Deriving a Constant for Chemical Equilibria

Because an equilibrium state is achieved when the forward reaction rate equals the reverse reaction rate, under a given set of conditions there must be a relationship between the composition of the system at equilibrium and the kinetics of a reaction (represented by rate constants). Let’s continue using the example of the decomposition of N₂O₄ to NO₂ to demonstrate this.  Both the forward and reverse reactions for this system consist of a single elementary reaction, so the reaction rates are as follows:

forward rate = k_f[N₂O₂]

and

reverse rate = k_r[NO₂]²

Note: You’ll learn all about rate expressions and expressing reaction rates in the chapter on kinetics, but for now, we’ll briefly explain these expressions. As previously mentioned, the rate constant, k, is unique to a particular reaction and helps mathematically define the rate of reaction. The concentration of reactant also determines the rate; the reason why NO₂ is squared in the expression for the reverse rate is because 2 molecules of NO₂ are required to form N₂O₄, as indicated in the chemical equilibrium equation. Note that the value of the exponent is based on the number of molecules of reactant only for elementary reactions; again don’t worry about understanding what this means right now, since it will be properly covered later on.

At equilibrium, the forward rate equals the reverse rate (definition of equilibrium):

k_f[N₂O₂] = k_r[NO₂]²

so

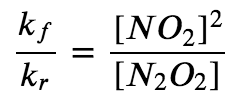
The ratio of the rate constants gives us a new constant, the equilibrium constant (K), which is defined as follows:

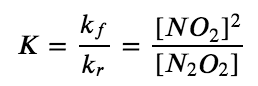
Hence there is a fundamental relationship between chemical kinetics and chemical equilibrium: under a given set of conditions, the composition of the equilibrium mixture is determined by the magnitudes of the rate constants for the forward and the reverse reactions. In other words, this equilibrium constant is equal to the rate constant for the forward reaction divided by the rate constant for the reverse reaction.

Measure of Reaction Extent

Because there is a direct relationship between the kinetics of a reaction and the equilibrium concentrations of products and reactants, when k_f ≫ k_r, K has a large value, and the concentration of products at equilibrium predominate. This corresponds to an essentially irreversible reaction. Conversely, when k_f ≪ k_r, K has a very small value, and the reaction produces almost no products as written. Systems for which k_f ≈ k_r have a value of K close to 1 and significant concentrations of both reactants and products at equilibrium.

Consider an equilibrium between substances A and B: A ⇌ B. The table below shows the percentage of moles of A and B that would be present at equilibrium for different values of K. At K values of 10^-5 and 10⁵, the mole percent of A and B are very nearly 100%, respectively. Hence, keep the following as a rule of thumb for this course: for K < 10^-5, the reaction is said to be “reactant-favoured” and consists of mostly reactant(s) with minimal product(s), whereas for K > 10⁵, the reaction practically proceeds to completion with little to no reactant(s) remaining.

Table 4.1.1 Relationship between the magnitude of K and mole percent of reactant and product.

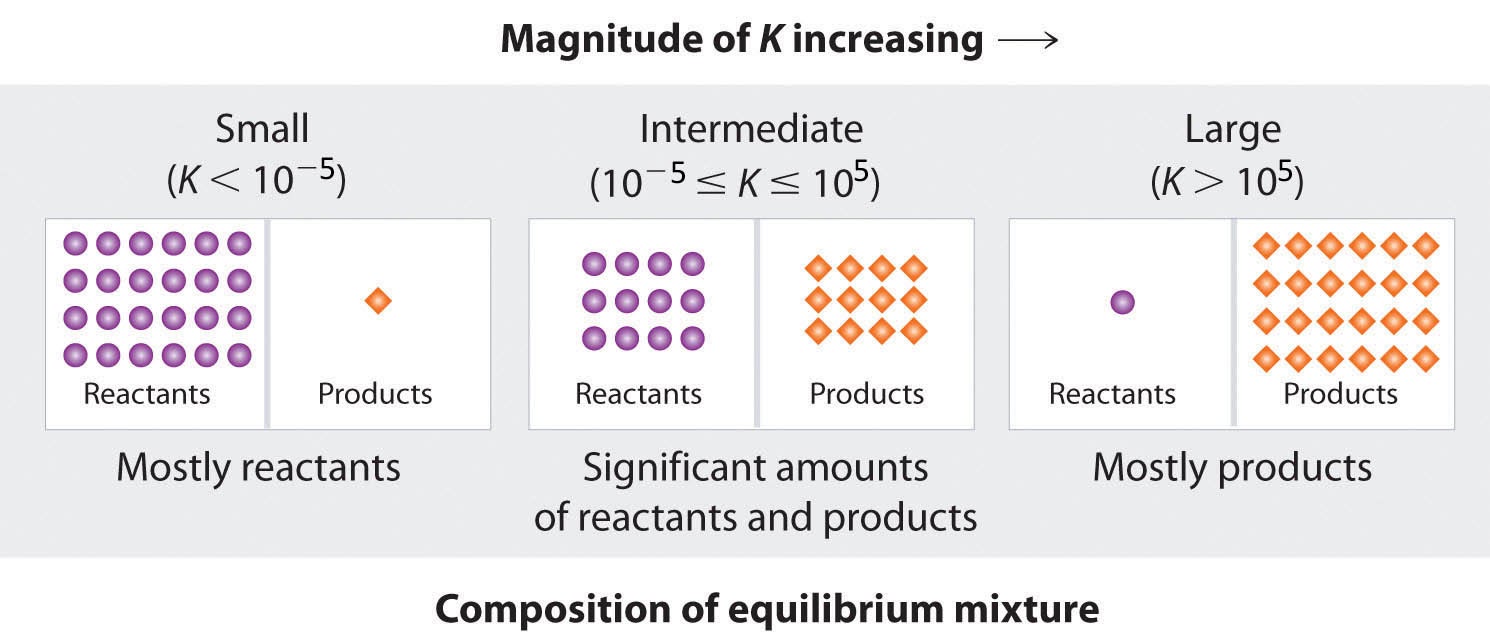
Figure 4.1.5. The larger the value of K, the farther the reaction proceeds to the right before equilibrium is reached, and the greater the ratio of products to reactants at equilibrium.

Let’s look at two examples of reactions to understand this:

The reaction between H₂ and Cl₂ to produce HCl has an equilibrium constant of 1.6 × 10³³ at 300 K. Because H₂ is a good reductant and Cl₂ is a good oxidant, the value of K is extremely large and the reaction proceeds essentially to completion. On the other hand, the reaction at 500 K between F₂ and two F atoms in the gas phase has an equilibrium constant of 7.4 × 10^-13. This K value is extremely small, indicating that the reactants don’t tend to form products readily – the formation and presence of reactants is heavily favoured.

Example 4.1.1 – Composition of Reactants/Products at Equilibrium

Predict which systems at equilibrium will (a) contain essentially only products, (b) contain essentially only reactants, and (c) contain appreciable amounts of both products and reactants.

(a) H₂ (g) + I₂ (g) ⇌ 2 HI (g)     K_{(700 K)} = 54

(b) 2 CO₂ (g) ⇌ 2 CO (g) + O₂ (g)     K_{(1200 K)} = 3.1 × 10^-18

(c) PCl₅ (g) ⇌ PCl₃ (g) + Cl₂ (g)     K_{(613 K)} = 97

(d) 2 O₃ (g) ⇌ 3 O₂ (g)     K_{(298 K)} = 5.9 × 10⁵⁵

Solution

(a) K is closer to 1 (10^-5 < K < 10⁵), so the equilibrium mixture will contain appreciable amounts of both products and reactants..

(b) K << 1 (K < 10^-5), so the reactants have little tendency to form products under the conditions specified; thus, at equilibrium the system will contain essentially only reactants.

(c) K is closer to 1 (10^-5 < K < 10⁵), so the equilibrium mixture will contain appreciable amounts of both products and reactants.

(d) K >> 1 (K > 10⁵), so at equilibrium it will consist of essentially only products.

Check Your Learning 4.1.1 – Composition of Reactants/Products at Equilibrium

Hydrogen and nitrogen react to form ammonia according to the following balanced chemical equation:

N₂ (g) + 3 H₂ (g)  ⇌  2 NH₃ (g)

Values of the equilibrium constant at various temperatures were reported as

K_25°C = 3.3 × 10⁸

K_177°C = 2.6 × 10³

K_327°C = 4.1

(a) At which temperature would you expect to find the highest proportion of H₂ and N₂ in the equilibrium mixture?

(b) Assuming that the reaction rates are fast enough so that equilibrium is reached quickly, at what temperature would you design a commercial reactor to operate to maximize the yield of ammonia?

Answer

(a) 327°C, where K is smallest; (b) 25°C, where K is largest

Questions

★ Questions

1. What does it mean to describe a reaction as “reversible”?

  2. When writing an equation, how is a reversible reaction distinguished from a          non reversible reaction?

  3. If a reaction is reversible, when can it be said to have reached equilibrium?

  4. Is a system at equilibrium if the rate constants of the forward and reverse              reactions are equal?

  5. If the concentrations of products and reactants are equal, is the system at              equilibrium?

Answers

1. The reaction can proceed in both the forward and reverse directions.

  2. Between the two types of reactions, they are distinguished by the arrows used      in the equation. In a reversible reaction “⇌” is appropriate, whereas in a non-              reversible reaction “→” is used.

  3. When a system has reached equilibrium, no further changes in the reactant and    product concentrations occur; the forward and reverse reactions continue to              occur, but at equivalent rates.

  4. Not necessarily; equivalent values of k_f and k_r (for the forward and reverse            directions) yield an equilibrium constant value of 1 (since K = k_f/k_r). However, this      does not mean that the system is at equilibrium. Only constant concentrations of      the reactant and products mean the reactions are at equilibrium. This does not          mean that their concentrations have to be equal, but in some cases they can be.

  5. The concept of equilibrium does not imply equal concentrations, though it is          possible.