3.6 – Hess’ Law
One way to report the heat absorbed or released would be to compile a massive set of reference tables that list the enthalpy changes for all possible chemical reactions, which would require an incredible amount of effort. Fortunately, Hess’s law, which we’ll discuss in this chapter, allows us to calculate the enthalpy change for virtually any conceivable chemical reaction using a relatively small set of tabulated data, such as the following:
- Enthalpy of combustion (ΔHcomb): The change in enthalpy that occurs during a combustion reaction. Enthalpy changes have been measured for the combustion of virtually any substance that will burn in oxygen; these values are usually reported as the enthalpy of combustion per mole of substance.
- Enthalpy of formation (ΔHf): The change in enthalpy due to the formation of a molecule from its elements in their natural state at standard conditions (ie. the state they are most stable at 25 C and 1 bar). As they are based on their elements, the enthalpy of formation for elements in their natural state is always equal to zero.
- Enthalpy of fusion (ΔHfus): The enthalpy change that accompanies the melting (fusion) of a mole of a substance; these values have been measured for almost all the elements and for most simple compounds.
- Enthalpy of vaporization (ΔHvap): The enthalpy change that accompanies the vaporization of 1 mol of a substance. The enthalpy change that accompanies the vaporization of 1 mol of a substance; these values have also been measured for nearly all the elements and for most volatile compounds.
- Enthalpy of solution (ΔHsoln): The change in enthalpy that occurs when a specified amount of solute dissolves in a given quantity of solvent. The enthalpy change when a specified amount of solute dissolves in a given quantity of solvent.
Enthalpy changes can be visualized using energy diagrams. The change in energy represents the enthalpy change after a chemical reaction has occurred.
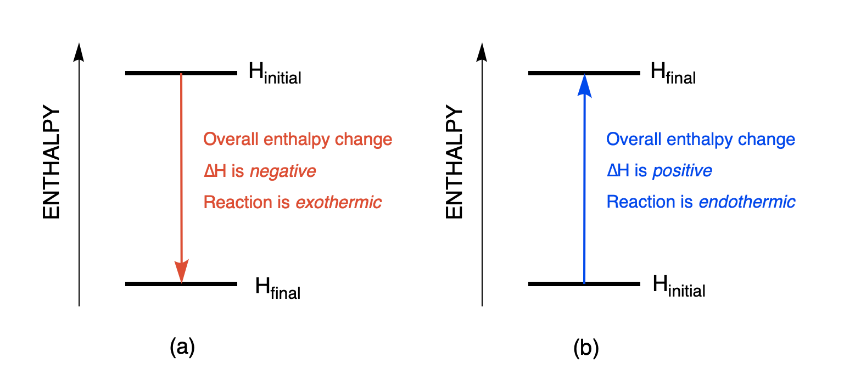
Figure 3.6.1. Enthalpy diagrams depicting the changes observed during an (a) exothermic and (b) endothermic reaction.
Enthalpy of Combustion
Standard enthalpy of combustion (ΔH°C) is the enthalpy change when 1 mole of a substance burns (combines vigorously with oxygen) under standard state conditions; it is sometimes called “heat of combustion.” For example, the enthalpy of combustion of ethanol, −1366.8 kJ/mol, is the amount of heat produced when one mole of ethanol undergoes complete combustion at 25 °C and 1 bar pressure, yielding products also at 25 °C and 1 bar.
C2H5OH (l) + 3 O2 (g) → 2 CO2 + 3 H2O (l) ΔH°298 = – 1366.8 kJ
It should be noted that, historically, the unit of standard pressure was 1 atmosphere (101.325 kPa) but this was changed by IUPAC in 1982 to 1 bar (100 kPa). Be aware that both of these values are still commonly used as standard pressure.
Enthalpies of combustion for many substances have been measured; a few of these are listed in Table 3.6.1. Many readily available substances with large enthalpies of combustion are used as fuels, including hydrogen, carbon (as coal or charcoal), and hydrocarbons (compounds containing only hydrogen and carbon), such as methane, propane, and the major components of gasoline.
Table 3.6.1 Standard Molar Enthalpies of Combustion
|
Substance
|
Combustion Reaction
|
Enthalpy of Combustion,
ΔH°C (kJ at 25°C)
|
|
carbon |
C (s) + O2 (g) → CO2 (g) |
−393.5 |
|
hydrogen |
H2 (g) + 1/2 O2 (g) → H2O (l) |
−285.8 |
|
magnesium |
Mg (s) + 1/2 O2 (g) → MgO (s) |
−601.6 |
|
sulfur |
S (s) + O2 (g) → SO2 (g) |
−296.8 |
|
carbon monoxide |
CO (g) + 1/2 O2 (g) → CO2 (g) |
−283.0 |
|
methane |
CH4 (g) + 2 O2 (g) → CO2 (g) + 2 H2O (l) |
−890.8 |
|
acetylene |
C2H2 (g) + 5/2 O2 (g) → 2 CO2 (g) + H2O (l) |
−1301.1 |
|
ethanol |
C2H5OH (l) + 3 O2 (g) → 2 CO2 (g) + 3 H2O (l) |
−1366.8 |
|
methanol |
CH3OH (l) + 3/2 O2 (g) → CO2 (g) + 2 H2O (l) |
−726.1 |
|
isooctane |
C8H18 (l) + 25/2 O2 (g) → 8 CO2 (g) + 9 H2O(l) |
−5461 |
Example 3.6.1 – Using Enthalpy of Combustion
As illustrated in Figure 3.6.2., the combustion of gasoline is a highly exothermic process. Let us determine the approximate amount of heat produced by burning 1.00 L of gasoline, assuming the enthalpy of combustion of gasoline is the same as that of isooctane, a common component of gasoline. The density of isooctane is 0.692 g/mL.
Figure 3.6.2. The combustion of gasoline is very exothermic. (credit: modification of work by “AlexEagle”/Flickr)
Solution
Starting with a known amount (1.00 L of isooctane), we can perform conversions between units until we arrive at the desired amount of heat or energy. The enthalpy of combustion of isooctane provides one of the necessary conversions. The table above gives this value as −5460 kJ per one mole of isooctane (C8H18).
Using these data,
The combustion of 1.00 L of isooctane produces 33,100 kJ of heat. (This amount of energy is enough to melt 99.2 kg of ice.)
Check Your Learning 3.6.1 – Using Enthalpy of Combustion
How much heat is produced by the combustion of 125 g of acetylene?
Answer
6.25 × 103 kJ
Emerging Algae-Based Energy Technologies (Biofuels)
As reserves of fossil fuels diminish and become more costly to extract, the search is ongoing for replacement fuel sources for the future. Among the most promising biofuels are those derived from algae (Figure 3.6.3.). The species of algae used are nontoxic, biodegradable, and among the world’s fastest-growing organisms. About 50% of the algal weight is oil, which can be readily converted into fuel such as biodiesel. Algae can yield 26,000 gallons of biofuel per hectare—much more energy per acre than other crops. Some strains of algae can flourish in brackish water that is not usable for growing other crops. Algae can produce biodiesel, biogasoline, ethanol, butanol, methane, and even jet fuel.
Figure 3.6.3. (a) Tiny algal organisms can be (b) grown in large quantities and eventually (c) turned into a useful fuel such as biodiesel. (credit a: modification of work by Micah Sittig; credit b: modification of work by Robert Kerton; credit c: modification of work by John F. Williams)
According to the US Department of Energy, only 39,000 square kilometres (about 0.4% of the landmass of the US or less than 1/7 of the area used to grow corn) can produce enough algal fuel to replace all the petroleum-based fuel used in the US. The cost of algal fuels is becoming more competitive—for instance, the US Air Force is producing jet fuel from algae at a total cost of under $5 USD per gallon. The process used to produce algal fuel is as follows: grow the algae (which use sunlight as their energy source and CO2 as a raw material); harvest the algae; extract the fuel compounds (or precursor compounds); process as necessary (e.g., perform a transesterification reaction to make biodiesel); purify, and distribute (Figure 3.6.3.).
Figure 3.6.4. Algae convert sunlight and carbon dioxide into oil that is harvested, extracted, purified, and transformed into a variety of renewable fuels.
Click here to learn more about the process of creating algae biofuel.
Standard Enthalpy of Formation
Standard enthalpy of formation ΔHf° is an enthalpy change for a reaction in which exactly one mole of a pure substance is formed from free elements in their most stable states under standard conditions. These values are especially useful for computing or predicting enthalpy changes for chemical reactions that are impractical or dangerous to carry out, or for processes for which it is difficult to make measurements. If we have values for the appropriate standard enthalpies of formation, we can determine the enthalpy change for any reaction, which we will practice here in this section.
The standard enthalpy of formation of CO2(g) is −393.5 kJ/mol. This is the enthalpy change for the exothermic reaction:
C (s) + O2 (g) → CO2 (g) ΔHf∘ = ΔH°298 = – 393.5 kJ
starting with the reactants at a pressure of 1 bar and 25 °C (with the carbon present as graphite, the most stable allotrope of carbon under these conditions) and ending with one mole of CO2, also at 1 bar and 25 °C. For nitrogen dioxide, NO2 (g), ΔHf° is 33.2 kJ/mol. This is the enthalpy change for the reaction:
1/2 N2 (g) + O2 (g) → NO2 (g) ΔHf∘ = ΔH°298 = + 33.2 kJ
A reaction equation with 1/2 mole of N2 and 1 mole of O2 is correct in this case because the standard enthalpy of formation always refers to 1 mole of product, NO2(g).
You will find a table of standard enthalpies of formation of many common substances in Appendix G. These values indicate that formation reactions range from highly exothermic (such as −2984 kJ/mol for the formation of P4O10) to strongly endothermic (such as +226.7 kJ/mol for the formation of acetylene, C2H2). By definition, the standard enthalpy of formation of an element in its most stable form is equal to zero under standard conditions, which is 1 bar for gases and 1 M for solutions. The reference forms used for most elements are simply the element itself (for example silver: Ag (s)), however, some are more unusual. These exceptions you are required to know for this course are summarized in the table below.
|
Unusal Element Reference Forms |
|
|
Element |
Reference Form |
|
hydrogen |
H2 (g) |
|
nitrogen |
N2 (g) |
|
oxygen |
O2 (g) |
|
fluorine |
F2 (g) |
|
chlorine |
Cl2 (g) |
|
bromine |
Br2 (l) |
|
iodine |
I2 (s) |
|
carbon |
C (graphite, s) |
|
phosphorus |
P (white, s) |
|
sulfur |
S8 (s) |
Table 3.6.2 Unusual Element Reference Forms
Example 3.6.2 – Evaluating an Enthalpy of Formation
Ozone, O3(g), forms from oxygen, O2(g), by an endothermic process. Ultraviolet radiation is the source of the energy that drives this reaction in the upper atmosphere. Assuming that both the reactants and products of the reaction are in their standard states, determine the standard enthalpy of formation, ΔHf° of ozone from the following information:
3 O2 (g) → 2 O3 (g) ΔH°298= + 286 kJ
Solution
ΔHf° is the enthalpy change for the formation of one mole of a substance in its standard state from the elements in their standard states. Thus, ΔHf° for O3(g) is the enthalpy change for the reaction:
For the formation of 2 mol of O3(g), ΔH°298=+286 kJ. This ratio,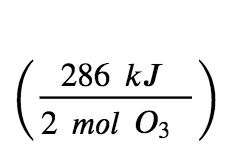 
, can be used as a conversion factor to find the heat produced when 1 mole of O3(g) is formed, which is the enthalpy of formation for O3(g):
Therefore, ΔHf°[ O3 (g)] = + 143 kJ/mol.
Check Your Learning 3.6.2 – Evaluating an Enthalpy of Formation
Hydrogen gas, H2, reacts explosively with gaseous chlorine, Cl2, to form hydrogen chloride, HCl(g). What is the enthalpy change for the reaction of 1 mole of H2(g) with 1 mole of Cl2(g) if both the reactants and products are at standard state conditions? The standard enthalpy of formation of HCl(g) is −92.3 kJ/mol.
Answer
H2 (g) + Cl2 (g) → 2 HCl (g) ΔH298∘ = – 184.6 kJ
Example 3.6.3 – Writing Reaction Equations for ΔHf°
Write the heat of formation reaction equations for:
(a) C2H5OH (l)
(b) Ca3(PO4)2 (s)
(c) C55H72O₅N₄Mg
(d) CaCO3
(e) Li2SO4
(f) Cu(NO3)2
Solution
Remembering that ΔHf° reaction equations are for forming 1 mole of the compound from its constituent elements under standard conditions, we have:
a. 2 C (s, graphite) + 3 H2 (g) + 1/2 O2 (g) → C2H5OH (l)
b. 3 Ca (s) + 1/2 P4 (s) + 4 O2 (g) → Ca3(PO4)2 (s)
c. 55 C (s, graphite) + 36 H2 (g) + 5/2 O2 (g) + 2 N2 (g) + Mg (s) → C55H72O₅N₄Mg
d. Ca (s) + C (s, graphite) + 3/2 O2(g) →CaCO3
e. 2 Li (s) + S (g) + 2 O2 (g) → Li2SO4
f. Cu (s) + 1 N2 (g) + 3O2 (g) → Cu(NO3)2
Note: The standard state of carbon is graphite, and phosphorus exists as P4.
Check Your Learning 3.6.3 – Writing Reaction Equations for ΔHf°
Write the heat of formation reaction equations for:
(a) C2H5OC2H5 (l)
(b) Na2CO3 (s)
Answer
a. 4 C (s, graphite) + 5 H2 (g) + 1/2 O2 (g) → C2H5OC2H (l)
b. 2 Na (s) + C (s, graphite) + 3/2 O2 (g) → Na3CO3 (s)
Hess’s Law
There are two ways to determine the amount of heat involved in a chemical change: measure it experimentally, or calculate it from other experimentally determined enthalpy changes. Some reactions are difficult, if not impossible, to investigate and make accurate measurements for experimentally. And even when a reaction is not hard to perform or measure, it is convenient to be able to determine the heat involved in a reaction without having to perform an experiment.
This type of calculation usually involves the use of Hess’s law, which states: If a process can be written as the sum of several stepwise processes, the enthalpy change of the total process equals the sum of the enthalpy changes of the various steps. Hess’s law is valid because enthalpy is a state function: Enthalpy changes depend only on where a chemical process starts and ends, but not on the path it takes from start to finish. For example, we can think of the reaction of carbon with oxygen to form carbon dioxide as occurring either directly or by a two-step process. The direct process is written:
C (s) + O2 (g) → CO2 (g) ΔH°298 = – 394 kJ
In the two-step process, first carbon monoxide is formed:
C (s) + 1/2 O2 (g) → CO2 (g) ΔH°298 = – 111 kJ
Then, carbon monoxide reacts further to form carbon dioxide:
CO (g) + 1/2 O2 (g) → CO2 (g) ΔH°298 = – 283 kJ
The equation describing the overall reaction is the sum of these two chemical changes:
Step 1: C (s) + 1/2 O2 (g) → CO2 (g) ΔH°298 = – 111 kJ
Step 2: CO (g) + 1/2 O2 (g) → CO2 (g) ΔH°298 = – 283 kJ
Sum: C (s) + O2 (g) + CO (g) → CO (g) + CO2 (g)
Because the CO produced in Step 1 is consumed in Step 2, the net change is:
C (s) + O2 (g) → CO2 (g) ΔH°298 = – 394 kJ
According to Hess’s law, the enthalpy change of the reaction will equal the sum of the enthalpy changes of the steps. We can apply the data from the experimental enthalpies of combustion in Table 3.6.1 to find the enthalpy change of the entire reaction from its two steps:
C (s) + 1/2 O2 (g) → CO2 (g) ΔH°298 = – 111 kJ
The result is shown in Figure 3.6.5. We see that ΔH of the overall reaction is the same whether it occurs in one step or two (i.e. it is a state function). This finding (overall ΔH for the reaction = sum of ΔH values for reaction “steps” in the overall reaction) is true in general for chemical and physical processes.
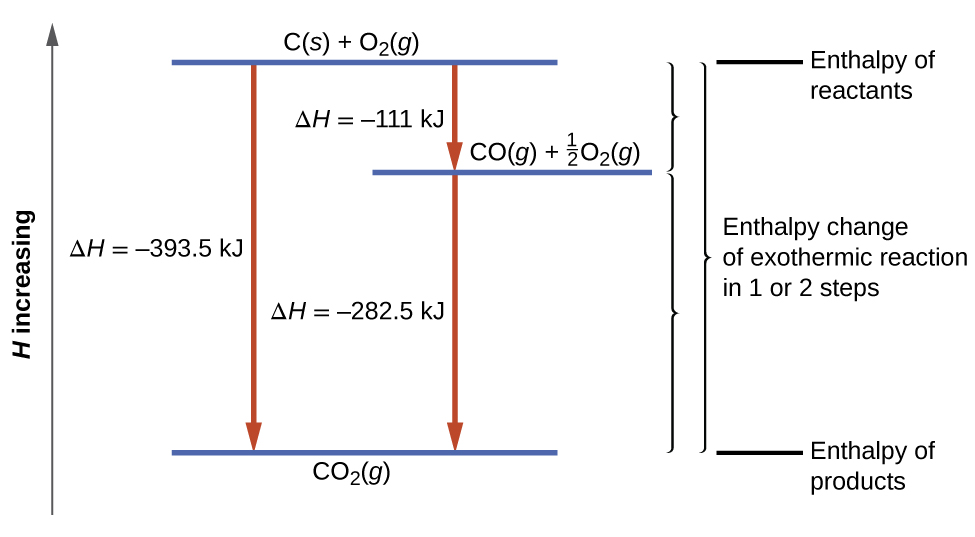
Figure 3.6.5. The formation of CO2(g) from its elements can be thought of as occurring in two steps, which sum to the overall reaction, as described by Hess’s law. The horizontal blue lines represent enthalpies. For an exothermic process, the products are at lower enthalpy than are the reactants.
Before we further practice using Hess’s law, let us recall two important features of ΔH.
ΔH is directly proportional to the quantities of reactants or products. For example, the enthalpy change for the reaction forming 1 mole of NO2(g) is +33.2 kJ:
When 2 moles of NO2 (twice as much) are formed, the ΔH will be twice as large:
N2 (g) + 2O2 (g) → 2 NO2 (g) ΔH = + 66.4 kJ
In general, if we multiply or divide an equation by a number, then the enthalpy change should also be multiplied or divided by the same number.
ΔH for a reaction in one direction is equal in magnitude and opposite in sign to ΔH for the reaction in the reverse direction. For example, given that:
H2 (g) + Cl2 (g) → 2 HCl (g) ΔH° = – 184.6 kJ
Then, for the “reverse” reaction, the enthalpy change is also “reversed”:
2 HCl (g) → H2 (g) + Cl2 (g) ΔH°=+184.6kJ
Example 3.6.4 – Stepwise Calculation of ΔHf° Using Hess’s Law
Determine the enthalpy of formation, ΔHf°, of FeCl3(s) from the enthalpy changes of the following two-step process that occurs under standard state conditions:
Fe (s) + Cl2 (g) → FeCl2 (s) ΔH=-341.8kJ
FeCl2 (s) + 1/2 Cl2 (g) → FeCl3 (s) ΔH = – 57.7 kJ
Solution
We are trying to find the standard enthalpy of formation of FeCl3(s), which is equal to ΔH° for the reaction:
Fe (s) + 3/2 Cl2 (g) → FeCl3 (s) ΔH°=ΔHf° FeCl3 (s)
= ?
Looking at the reactions, we see that the reaction for which we want to find ΔH° is the sum of the two reactions with known ΔH values, so we must sum their enthalpies:
Fe (s) + Cl2 (g) → FeCl2 (s) ΔH∘ = – 341.8 kJ
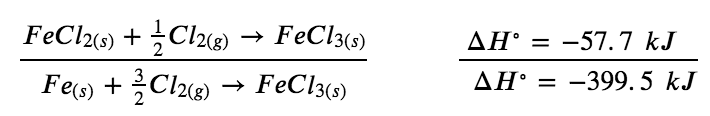
The enthalpy of formation, ΔHf°, of FeCl3(s) is − 399.5 kJ/mol.
Check Your Learning 3.6.4 – Stepwise Calculation of ΔHf° Using Hess’s Law
Calculate ΔH for the process:
N2 (g) + 2 O2 (g) → 2 NO2 (g)
from the following information:
N2 (g) + 2 O2 (g) → 2 NO2 (g) ΔH = 180.5 kJ
NO (g) + 1/2 O2 (g) → NO2 (g) ΔH = – 57.06 kJ
Answer
66.4 kJ
Here is a less straightforward example that illustrates the thought process involved in solving many Hess’s law problems. It shows how we can find many standard enthalpies of formation (and other values of ΔH) if they are difficult to determine experimentally.
Example 3.6.5 – A More Challenging Problem Using Hess’s Law
Chlorine monofluoride can react with fluorine to form chlorine trifluoride:
(i) ClF (g) + F2 (g) → ClF3 (g) ΔH° = ?
Use the reactions here to determine the ΔH° for reaction (i):
(ii) 2 OF2 (g) → O2 (g) + 2 F2 (g) ΔH°(ii) = – 49.4 kJ
(iii) 2 ClF2 (g) + O2 (g) → Cl2O (g) + OF2 (g) ΔH°(iii) = + 205.6 kJ
(iv) ClF3 (g) + O2 (g) → 1/2 Cl2O (g) + 3/2 OF2 (g) ΔH°(iv)= + 266.7 kJ
Solution
Our goal is to manipulate and combine reactions (ii), (iii), and (iv) such that they add up to reaction (i). Going from left to right in (i), we first see that ClF(g) is needed as a reactant. This can be obtained by multiplying reaction (iii) by 1/2, which means that the ΔH° change is also multiplied by 1/2:
ClF (g) + 1/2 O2 (g) → 1/2 Cl2O (g) + 1/2 OF2 (g)
Next, we see that F2 is also needed as a reactant. To get this, reverse and halve reaction (ii), which means that the ΔH° changes sign and is halved:
To get ClF3 as a product, reverse (iv), changing the sign of ΔH°:
Now check to make sure that these reactions add up to the reaction we want:
ClF (g) + 1/2 O2 (g) → 1/2 Cl2O (g) + 1/2 OF2 (g)
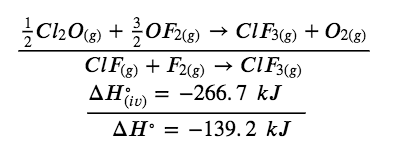
Reactants 1/2 O2 and 1/2 O2 cancel out product O2; product 1/2 Cl2O cancels reactant 1/2 Cl2O;, and reactant 3/2 OF2 is cancelled by products 1/2 OF2 and OF2. This leaves only reactants ClF(g) and F2(g) and product ClF3(g), which are what we want. Since summing these three modified reactions yields the reaction of interest, summing the three modified ΔH° values will give the desired ΔH°:
ΔH∘ = (+ 102.8 kJ) + (24.7 kJ) + (- 266.7 kJ) = – 139.2 kJ
Check Your Learning 3.6.6 – A More Challenging Problem Using Hess’s Law
Aluminum chloride can be formed from its elements:
(i) 2 Al (s) + 3 Cl2 (g) → 2 AlCl3 (s) ΔH°=?
Use the reactions here to determine the ΔH° for reaction (i):
(ii) HCl (g) → HCl (aq) ΔH°(ii) = – 74.8 kJ
(iii) H2 (g) + Cl2 (g) → 2 HCl (g) ΔH°(iii) = – 185 kJ
(iv) AlCl3 (aq) → AlCl3 (s) ΔH°(iv) = + 323 kJ/mol
(v) 2 Al (s) + 6 HCl (aq) → 2 AlCl3 (aq) + 3 H2 (g) ΔH°(v) = + 1049 kJ
Answer
−1407 kJ
We also can use Hess’s law to determine the enthalpy change of any reaction if the corresponding enthalpies of formation of the reactants and products are available. The stepwise reactions we consider are (i) decompositions of the reactants into their component elements (for which the enthalpy changes are proportional to the negative of the enthalpies of formation of the reactants), followed by (ii) re-combinations of the elements to give the products (with the enthalpy changes proportional to the enthalpies of formation of the products). The standard enthalpy change of the overall reaction is therefore equal to (ii) the sum of the standard enthalpies of formation of all the products plus (i) the sum of the negatives of the standard enthalpies of formation of the reactants. This is usually rearranged slightly to be written as follows, with ∑ representing “the sum of” and n standing for the stoichiometric coefficients:
ΔHreaction∘ = Σn × ΔH°f(products) – Σn × ΔH°f(reactants)
The following example shows in detail why this equation is valid, and how to use it to calculate the enthalpy change for a reaction of interest.
Example 3.6.7 – Using Hess’s Law
What is the standard enthalpy change for the reaction:
3 NO2 (g) + H2O (l) → 2 HNO3 (aq) + NO (g) ΔH° = ?
Solution:
Using the Equation
Use the special form of Hess’s law given previously:
ΔH°reaction= Σn × ΔH°f(products) – Σn × ΔH°f(reactants)
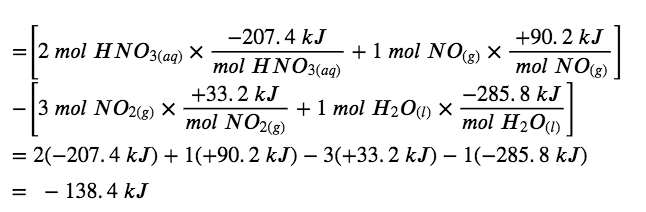
Support For Why the General Equation Is Valid
Alternatively, we can write this reaction as the sum of the decompositions of 3 NO2(g) and 1 H2O(l) into their constituent elements, and the formation of 2 HNO3(aq) and 1 NO(g) from their constituent elements. Writing out these reactions, and noting their relationships to the ΔHf° values for these compounds (from Appendix G), we have:
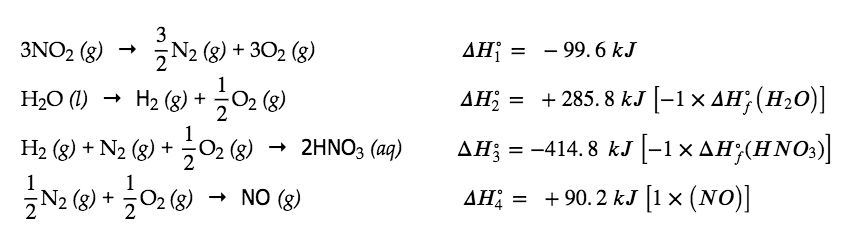
Summing these reaction equations gives the reaction we are interested in:
3 NO2 (g) + H2O (l) → 2 HNO3 (aq) + NO (g)
Summing their enthalpy changes gives the value we want to determine:
ΔHrxn∘ = ΔH1° + ΔH2° + ΔH3° + ΔH4°∘
= (- 99.6 kJ) + (+ 285.8 kJ) + (- 414.8 kJ) + (+ 90.2 kJ)
=-138.4kJ
So the standard enthalpy change for this reaction is ΔH° = −138.4 kJ.
Note that this result was obtained by (1) multiplying the ΔHf° of each product by its stoichiometric coefficient and summing those values, (2) multiplying the ΔHf° of each reactant by its stoichiometric coefficient and summing those values, and then (3) subtracting the result found in (2) from the result found in (1). This is also the procedure in using the general equation, as shown.
For a more in-depth explanation of this approach, check out the
Check Your Learning 3.6.7 – Using Hess’s Law
Calculate the heat of combustion of 1 mole of ethanol, C2H5OH (l), when H2O (l) and CO2 (g) are formed. Use the following enthalpies of formation: C2H5OH (l), −278 kJ/mol; H2O (l), −286 kJ/mol; and CO2 (g), −394 kJ/mol.
Answer
−1368 kJ/mol
Questions
★ Questions
1. How much heat is produced when 100 mL of 0.250 M HCl (density, 1.00 g/mL) and 200 mL of 0.150 M NaOH (density, 1.00 g/mL) are mixed?
HCl (aq) + NaOH (aq) → NaCl (aq) + H2O (l) ΔH298∘ = – 58 kJ
If both solutions are at the same temperature and the heat capacity of the products is 4.19 J/g °C, how much will the temperature increase? What assumption did you make in your calculation?
2. Before the introduction of chlorofluorocarbons, sulfur dioxide (enthalpy of vaporization, 6.00 kcal/mol) was used in household refrigerators. What mass of SO2 must be evaporated to remove as much heat as evaporation of 1.00 kg of CCl2F2 (enthalpy of vaporization is 17.4 kJ/mol)? The vaporization reactions for SO2 and CCl2F2 are SO2 (l) ⟶ SO2 (g) and CCl2F (l) ⟶ CCl2F2 (g), respectively.
3. Homes may be heated by pumping hot water through radiators. What mass of water will provide the same amount of heat when cooled from 95.0 to 35.0 °C, as the heat provided when 100 g of steam is cooled from 110 °C to 100 °C.
4. Does the standard enthalpy of formation of H2O (g) differ from ΔH° for the reaction 2 H2 (g) + O2 (g) ⟶ 2 H2O (g) ?
5. Joseph Priestly prepared oxygen in 1774 by heating red mercury(II) oxide with sunlight focused through a lens. How much heat is required to decompose exactly 1 mole of red HgO(s) to Hg(l) and O2(g) under standard conditions?
6. How many kilojoules of heat will be released when exactly 1 mole of manganese, Mn, is burned to form Mn3O4(s) at standard state conditions?
★★ Questions
7. The following sequence of reactions occurs in the commercial production of aqueous nitric acid:
4 NH3 (g) + 5 O2 (g) → 4 NO (g) + 6 H2O (l) ΔH = – 907 kJ
2 NO (g) + O2 (g) → 2 NO (g) ΔH = – 113 kJ
3 NO2 + H2O (l) → 2 HNO3 (aq) + NO (g) ΔH = – 139 kJ
Determine the total energy change for the production of one mole of aqueous nitric acid by this process.
8. Both graphite and diamond burn.
C (s, diamond) + O2 (g) → CO2 (g)
For the conversion of graphite to diamond:
C (s, diamond) → CO2 (g) ΔH298∘ = 1.90 kJ
Which produces more heat, the combustion of graphite or the combustion of diamond?
9. From the molar heats of formation in Appendix G, determine how much heat is required to evaporate one mole of water:
H2O (l) → H2O (g)
10. Calculate ΔH298° for the process
Sb (s) + 5/2 Cl2 (g) → SbCl5 (g)
from the following information:
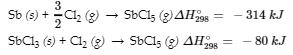
11. Calculate ΔH298° for the process
Zn (s) + S (s) + 2O2 (g) → ZnSO4 (s)
from the following information:
Zn (s) + S (s) → ZnS (s) ΔH298∘ = – 206.0 kJ
ZnS (s) + 2 O2 (g) → ZnSO4 (s) ΔH298∘ = – 776.8 kJ
12. Calculate the standard molar enthalpy of formation of NO(g) from the following data:
N2 (g) + 2 O2 → 2 NO2 (g) ΔH298∘ = 66.4 kJ
2 NO (g) + O2 → 2 NO2 (g) ΔH298∘ = – 114.1 kJ
13. Using the data in Appendix G, calculate the standard enthalpy change for each of the following reactions:
a. N2 (g) + O2 (g) → 2 NO (g)
b. Si (s) + 2 Cl2 (g) → SiCl4 (g)
c. Fe2O3 (s) + 3 H2 (g) → 2 Fe (s) + 3 H2O (l)
d. 2 LiOH (s) + Co2 (g) → Li2CO3 (s) + H2O (g)
14. The following reactions can be used to prepare samples of metals. Determine the enthalpy change under standard state conditions for each.
a. 2 Ag2O (s) → 4 Ag (s) + O2 (g)
b. SnO (s) + CO (g) → Sn (s) + CO2 (g)
c. Cr2O3 (s) + 3 H2 (g) → 2 Cr (s) + 3 H2O (l)
d. 2 Al (s) + Fe2O3 (s) → Al2O3 (s) + 2 Fe (s)
15. Calculate the enthalpy of combustion of propane, C3H8(g), for the formation of H2O(g) and CO2(g). The enthalpy of formation of propane is −104 kJ/mol.
16. Both propane and butane are used as gaseous fuels. Which compound produces more heat per gram when burned?
★★★ Questions
17. Ethanol, C2H5OH, is used as a fuel for motor vehicles, particularly in Brazil.
a. Write the balanced equation for the combustion of ethanol to CO2 (g) and H2O (g), and, using the data in Appendix G, calculate the enthalpy of combustion of 1 mole of ethanol.
b. The density of ethanol is 0.7893 g/mL. Calculate the enthalpy of combustion of exactly 1 L of ethanol.
c. Assuming that an automobile’s mileage is directly proportional to the heat of combustion of the fuel, calculate how much farther an automobile could be expected to travel on 1 L of gasoline than on 1 L of ethanol. Assume that gasoline has the heat of combustion and the density of n–octane, C8H18 (ΔHf° = − 208.4 kJ/mol; density = 0.7025 g/mL).
18. Among the substances that react with oxygen and that have been considered as potential rocket fuels are diborane [B2H6, produces B2O3(s) and H2O(g)], methane [CH4, produces CO2(g) and H2O(g)], and hydrazine [N2H4, produces N2(g) and H2O(g)]. On the basis of the heat released by 1.00 g of each substance in its reaction with oxygen, which of these compounds offers the best possibility as a rocket fuel? The ΔHf° of B2H6(g), CH4(g), and N2H4(l) may be found in Appendix G.
19. The oxidation of the sugar glucose, C6H12O6, is described by the following equation:
C6H12O6 (s) + 6 O2 (g) → 6 CO2 (g) + 6 H2O (l) ΔH = – 2816 kJ
The metabolism of glucose gives the same products, although the glucose reacts with oxygen in a series of steps in the body.
a. How much heat in kilojoules can be produced by the metabolism of 1.0 g of glucose?
b. How many Calories can be produced by the metabolism of 1.0 g of glucose?
20. During a recent winter month in Sheboygan, Wisconsin, it was necessary to obtain 3500 kWh of heat provided by a natural gas furnace with 89% efficiency to keep a small house warm (the efficiency of a gas furnace is the percent of the heat produced by combustion that is transferred into the house).
a. Assume that natural gas is pure methane and determine the volume of natural gas in cubic feet that was required to heat the house. The average temperature of the natural gas was 56 °F; at this temperature and a pressure of 1 atm, natural gas has a density of 0.681 g/L.
b. How many gallons of LPG (liquefied petroleum gas) would be required to replace the natural gas used? Assume the LPG is liquid propane [C3H8: density, 0.5318 g/mL; enthalpy of combustion, 2219 kJ/mol for the formation of CO2(g) and H2O(l)] and the furnace used to burn the LPG has the same efficiency as the gas furnace.
c. What mass of carbon dioxide is produced by combustion of the methane used to heat the house?
d. What mass of water is produced by combustion of the methane used to heat the house?
e. What volume of air is required to provide the oxygen for the combustion of the methane used to heat the house? Air contains 23% oxygen by mass. The average density of air during the month was 1.22 g/L.
f. How many kilowatt-hours (1 kWh = 3.6 × 106 J) of electricity would be required to provide the heat necessary to heat the house? Note electricity is 100% efficient in producing heat inside a house.
g. Although electricity is 100% efficient in producing heat inside a house, the production and distribution of electricity is not 100% efficient. The efficiency of production and distribution of electricity produced in a coal-fired power plant is about 40%. A certain type of coal provides 2.26 kWh per pound upon combustion. What mass of this coal in kilograms will be required to produce the electrical energy necessary to heat the house if the efficiency of generation and distribution is 40%?
Answers
2. 367.12 g
3. 7.43 g
4. No.
5. 90.8 kJ
6. 459.6 kJ
7. −495 kJ/mol
8. Combustion of diamond produces more heat
9. 44.01 kJ/mol
10. −394 kJ
11. – 207 kJ
12. 90.3 mol−1 of NO
13. (a) 90.4 kJ/mol, (b) 105 kJ/mol, (c) -538.37 kJ/mol, (d) 94.49 kJ/mol
14. (a) 62.2 kJ/mol, (b) 3.2 kJ/mol, (c) 271 kJ/mol, (d) -847.6 kJ/mol
15. – 2044 kJ
16. Propane
17. (a) C2H5OH + 3O2 (g) → 2CO2 (g) + 3H2O (g), -1234.8 kJ/mol, (b) -21187.56 kJ, (c) 44% Farther
18. On the assumption that the best rocket fuel is the one that gives off the most heat, B2H6 is the prime candidate.
19. (a) 15.63 kJ/g, (b) 3.74 cal/g
20. (a) 13260 cubic feet, (b) 141.2 gallons, (c) 701.52 kg, (d) 574.32 kg, (e) 3635637.26 L, (f) 3500 kWh, (g) 1756.34 kg
Heat released when one mole of a compound undergoes complete combustion under standard conditions
Compound composed only of hydrogen and carbon; the major component of fossil fuels
Enthalpy change of a chemical reaction in which 1 mole of a pure substance is formed from its elements in their most stable states under standard state conditions
If a process can be represented as the sum of several steps, the enthalpy change of the process equals the sum of the enthalpy changes of the steps
