Solutions: Case Study – Sulpher Dioxide
1. How much will the firms pollute before policy intervention?
Without policy intervention, there is no benefit for a firm to decrease its pollution. Even though reducing the first few units costs relatively little, the firm maximizes profits by polluting its full amount of pollution, where the costs of abatement are 0. This results in Firm 1 polluting 10 million tons of Sulpher Dioxide, and Firm 2 polluting 20 million tons, for a total of 30 million tons.
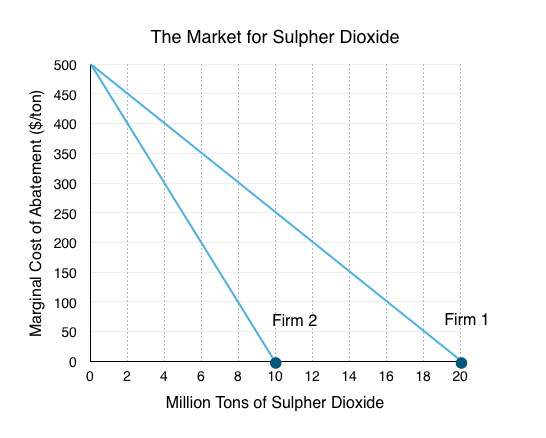
2. If the government implemented a cap and trade system, distributing a total of 12 million permits, with 6 million to each firm, who would sell and who would buy permits?
Since we know that each firm is given 6 million permits, we need to compare the marginal cost of abatement for each firm at that level. Drawing a line up from 6 million we see that for Firm 1, their marginal cost of abatement is $350, whereas Firm 2 faces a cost of $200. Since Firm 1 values pollution more that Firm 2, there are mutually beneficial exchanges where Firm 1 buys permits from Firm 2.
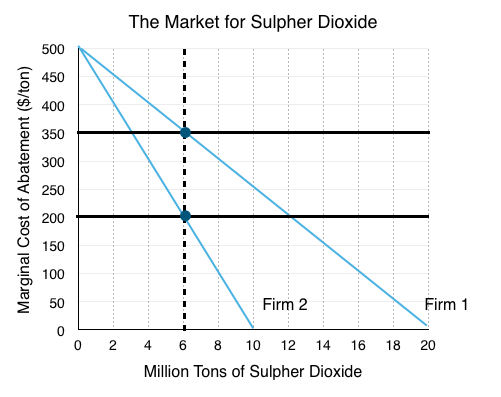
3. How much would the seller be willing to accept, and how much will the buyer be willing to pay?
At 6 million permits, we can see that Firm 1 is willing to pay up to their marginal cost of abatement, or $350, and Firm 2 is willing to accept at least enough to cover their lost benefit from polluting, or $200. Notice that after Firm 1 buys a permit from Firm 2, this relationship changes – Firm 1 will be willing to pay slightly less, and Firm 2 will need to be paid slightly more.
4. What is the equilibrium price of permits, and the equilibrium quantity of Sulpher Dioxide production? After the exchange of permits on the open market, how much does each firm emit?
To find the equilibrium price and quantity, we need to find a price level for permits such that the marginal cost of abatement for both firms is equal. By looking at our previous graph, and following what happens each time Firm 1 buys a permit from Firm 2, we see that Firm 1’s marginal cost falls and Firm 2’s marginal cost rises until they are equal.
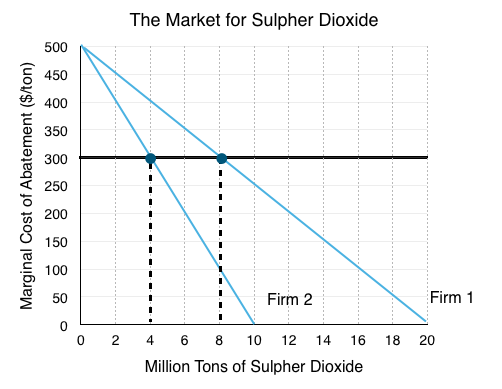
The transactions continue until Firm 1 has 8 million permits and Firm 2 has 4 million units. At this point the marginal costs of abatement are equal so no mutually beneficial transactions exist. Equilibrium quantity is 12 million, as regulated by the government, and the market price for permits is $300.
5. What are the total benefits and total costs to each firm from trading permits? Show that the trade was a Pareto Improvement
For Firm 1, buying more permits gives them the benefit of polluting more, which is equal to the reduction of the costs of abatement as shown in the green area. The cost is the amount they have to pay Firm 2, which is equal to the market price of the permit ($300) multiplied by the number they purchase as shown in the red area.
Note that while Firm 1 is technically willing to pay more than $300, in the perfectly competitive market for permits we usually deal with, if Firm 2 tries to charge any more than $300, Firm 1 will purchase permits from another firm.
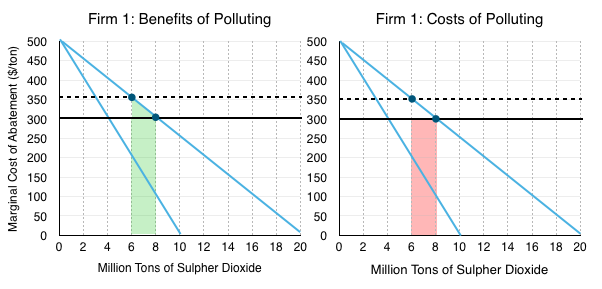
Calculating costs and benefits:
Benefits (green area):
[$300 x (8-6)] + [($350-$300) x (8-6)]/2
=$650 million
Costs (red area):
[$300 x (8-6)]
=$600 million
Surplus:
$650 million – $600 million
=$50 million
For Firm 2, selling permits means they will have to pollute less. This cost of abatement is equal to the red area below, and is the down side for selling permits. This cost is outweighed by the benefit of selling permits at the market price of $300. The revenue Firm 2 receives is depicted in the green area.
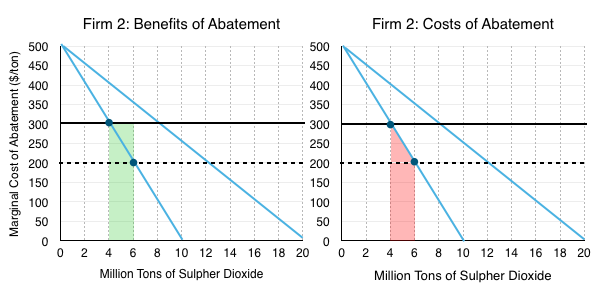
Calculating costs and benefits:
Benefits (green area):
[$300 x (6-4)] + [($350-$300) x (6-4)]/2
=$600 million
Costs (red area):
[$200 x (6-4)] + [($300-$200) x (6-4)]/2
=$500 million
Surplus:
$600 million – $500 million
=$100 million
We can see that since both firms benefited from the trade, that this is indeed a Pareto improvement from when they were each emitting 6 million tons of Sulpher Dioxide. The total surplus gain is equal to $150 million ($50 million + $100 million).
6. What is the correct tax level to receive the same result as in question 2?
The tax level to give us the same result as before is equal to the market price of permits. This price incentives the same action from Firms 1 and 2, but rather than making trades with each other, they are making decisions on whether or not to abate on the margin with consideration of the tax. They will abate as long as there marginal cost of abatement is lower than the tax rate.
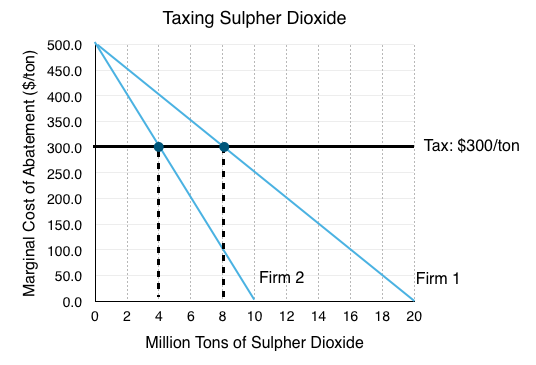
7. How much revenue will the government raise from the tax?
The government earns $300/ton of Sulpher Dioxide emitted. Since total emissions are 12 million tons, the government will make $3.6 billion. ($300 x 12 million)
8. What assumptions does the government have to make under cap and trade? What about under the carbon tax?
Under cap and trade the government has to make assumptions and decide on the quantity to cap emissions, whereas under a carbon tax, the government has to make assumptions and decide on the price to tax emissions. If the government wants to reduce emissions by 50%, with a carbon tax it would have to know the marginal cost of abatement for each of the firms. With cap and trade, they just need to know how much firms are emitting. Of course, as mentioned in the following explanation of the EU policy, sometimes emissions will change as a result of changing demand, which can make it difficult to set the right quantity under cap and trade.
9. If the government implemented a cap and trade system, distributing a total of 16 billion permits, how much will emissions be reduced by as a result of this policy?
In this case, since we don’t know the initial distribution of the permits, we can skip right to the result of the cap and trade. Knowing that firms will trade permits until the marginal cost of abatement is equal, we need to find a horizontal line where the total amount of pollution sums to 16 billion tons of Carbon. As shown in the graph below, this occurs at a price of $0/permit. This means that the government actually gave out enough permits for the firms to continue to pollute at the levels they had before the cap and trade program, rendering the policy ineffective.

10. If the government wanted to reduce emissions by 50% by purchasing permits, what is the minimum amount they would have to pay?
After trades, we know that Firm 1 will end up with 12 billion permits, and Firm 2 will end up with 4 billion permits. If the government wants to reduce emissions by 50% they will have to purchase 8 billion permits to make the new pollution levels 8 billion. We can quickly identify that the equilibrium price for 8 billion permits is $15, so one way the government could reduce pollution is offer $15 to the firms.
Notice however that the government could get away with paying less. As long as they pay the firms for the marginal cost of abating to 8 billion tons of Carbon, the firms will be indifferent to abating or not.
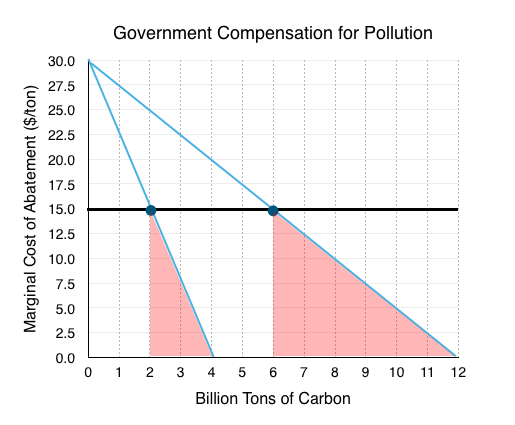
Calculating the total abatement costs:
Firm 1 – Abating from 12 billion to 6 billion (Area A):
$15 x (12 – 6) = $90 billion
Firm 2 – Abating from 4 billion to 2 billion (Area B):
$15 x (4 – 2) = $30 billion
Total Costs to the Government
$90 billion + $30 billion = $120 billion
As shown, trying to purchase permits out of the market can become quite expensive.

