23. Respiratory System Infections

23.3 Viral Infections of the Respiratory Tract

Learning Objectives

  • Identify the most common viruses that can cause infections of the upper and lower respiratory tract
  • Compare the major characteristics of specific viral diseases of the respiratory tract

Viruses are the most frequent cause of respiratory tract infections. Unlike the bacterial pathogens, we have few effective therapies to combat viral respiratory infections. Fortunately, many of these diseases are mild and self-limiting. A few respiratory infections manifest their primary symptoms at other locations in the body.

The Common Cold

The common cold is a generic term for a variety of mild viral infections of the nasal cavity. More than 200 different viruses are known to cause the common cold. The most common groups of cold viruses include rhinoviruses, coronaviruses, and adenoviruses. These infections are widely disseminated in the human population and are transmitted through direct contact and droplet transmission. Coughing and sneezing efficiently produce infectious aerosols, and rhinoviruses are known to persist on environmental surfaces for up to a week.[1]

Viral contact with the nasal mucosa or eyes can lead to infection. Rhinoviruses tend to replicate best between 33 °C (91.4 °F) and 35 °C (95 °F), somewhat below normal body temperature (37 °C [98.6 °F]). As a consequence, they tend to infect the cooler tissues of the nasal cavities. Colds are marked by an irritation of the mucosa that leads to an inflammatory response. This produces common signs and symptoms such as nasal excess nasal secretions (runny nose), congestion, sore throat, coughing, and sneezing. The absence of high fever is typically used to differentiate common colds from other viral infections, like influenza. Some colds may progress to cause otitis media, pharyngitis, or laryngitis, and patients may also experience headaches and body aches. The disease, however, is self-limiting and typically resolves within 1–2 weeks.

There are no effective antiviral treatments for the common cold and antibacterial drugs should not be prescribed unless secondary bacterial infections have been established. Many of the viruses that cause colds are related, so immunity develops throughout life. Given the number of viruses that cause colds, however, individuals are never likely to develop immunity to all causes of the common cold.

  • How are colds transmitted?
  • What is responsible for the symptoms of a cold?

CLINICAL FOCUS: Part 3

Since antibiotic treatment had proven ineffective, John’s doctor suspects that a viral or fungal pathogen may be the culprit behind John’s case of pneumonia. Another possibility is that John could have an antibiotic-resistant bacterial infection that will require a different antibiotic or combination of antibiotics to clear.

The RIDT tests both came back negative for type A and type B influenza. However, the diagnostic laboratory identified the sputum isolate as Legionella pneumophila. The doctor ordered tests of John’s urine and, on the second day after his admission, results of an enzyme immunoassay (EIA) were positive for the Legionella antigen. John’s doctor added levofloxacin to his antibiotic therapy and continued to monitor him. The doctor also began to ask John where he had been over the past 10 to 14 days.

  • Do negative RIDT results absolutely rule out influenza virus as the etiologic agent? Why or why not?
  • What is John’s prognosis?

Jump to the next Clinical Focus box. Go back to the previous Clinical Focus box.

Influenza

Commonly known as the flu, influenza is a common viral disease of the lower respiratory system caused by an orthomyxovirus. Influenza is pervasive worldwide and causes 3,000–50,000 deaths each year in the United States. The annual mortality rate can vary greatly depending on the virulence of the strain(s) responsible for seasonal epidemics. [2]

Influenza infections are most typically characterized by fever, chills, and body aches. This is followed by symptoms similar to the common cold that may last a week or more. Table 23.4 compares the signs and symptoms of influenza and the common cold.

Table 23.4. Comparison of the Common Cold and Influenza

Comparing the Common Cold and Influenza
Sign/Symptom Common Cold Influenza
Fever Low (37.2 °C [99 °F]) High (39 °C [102.2 °F])
Headache Common Common
Aches and pains Mild Severe
Fatigue Slight Severe
Nasal congestion Common Rare
Sneezing Common Rare

In general, influenza is self-limiting. However, serious cases can lead to pneumonia and other complications that can be fatal. Such cases are more common in the very young and the elderly; however, certain strains of influenza virus (like the 1918–1919 variant discussed later in this chapter) are more lethal to young adults than to the very young or old. Strains that affect young adults are believed to involve a cytokine storm—a positive feedback loop that forms between cytokine production and leukocytes. This cytokine storm produces an acute inflammatory response that leads to rapid fluid accumulation in the lungs, culminating in pulmonary failure. In such cases, the ability to mount a vigorous immune response is actually detrimental to the patient. The very young and very old are less susceptible to this effect because their immune systems are less robust.

A complication of influenza that occurs primarily in children and teenagers is Reye syndrome. This sequela causes swelling in the liver and brain, and may progress to neurological damage, coma, or death. Reye syndrome may follow other viral infections, like chickenpox, and has been associated with the use of aspirin. For this reason, the CDC and other agencies recommend that aspirin and products containing aspirin never be used to treat viral illnesses in children younger than age 19 years.[3]

The influenza virus is primarily transmitted by direct contact and inhalation of aerosols. The RNA genome of this virus exists as seven or eight segments, each coated with ribonucleoprotein and encoding one or two specific viral proteins. The influenza virus is surrounded by a lipid membrane envelope, and two of the main antigens of the influenza virus are the spike proteins hemagglutinin (H) and neuraminidase (N), as shown in Figure 23.15. These spike proteins play important roles in the viral infectious cycle.

A sphere with strand of circles in the inside – this strand is labeled ribonucleoprotein. The outside of the sphere is made of 2 layers. The inner layer is the capsid. The outer layer is the lipid envelope. The lipid envelope has an M2 ion channel and two different surface components labeled hemagglutinin (H) and neuraminidase (N).
Figure 23.15. The illustration shows the structure of an influenza virus. The viral envelope is studded with copies of the proteins neuraminidase and hemagglutinin, and surrounds the individual seven or eight RNA genome segments. [Credit: modification of work by Dan Higgins, Centers for Disease Control and Prevention]

Following inhalation, the influenza virus uses the hemagglutinin protein to bind to sialic acid receptors on host respiratory epithelial cells. This facilitates endocytosis of the viral particle. Once inside the host cell, the negative strand viral RNA is replicated by the viral RNA polymerase to form mRNA, which is translated by the host to produce viral proteins. Additional viral RNA molecules are transcribed to produce viral genomic RNA, which assemble with viral proteins to form mature virions. Release of the virions from the host cell is facilitated by viral neuraminidase, which cleaves sialic-acid receptors to allow progeny viruses to make a clean exit when budding from an infected cell.

There are three genetically related influenza viruses, called A, B, and C. The influenza A viruses have different subtypes based on the structure of their hemagglutinin and neuraminidase proteins. There are currently 18 known subtypes of hemagglutinin and 11 known subtypes of neuraminidase. Influenza viruses are serologically characterized by the type of H and N proteins that they possess. Of the nearly 200 different combinations of H and N, only a few, such as the H1N1 strain, are associated with human disease. The influenza viruses A, B, and C make up three of the five major groups of orthomyxoviruses. The differences between the three types of influenza are summarized in Table 23.5. The most virulent group is the influenza A viruses, which cause seasonal pandemics of influenza each year. Influenza A virus can infect a variety of animals, including pigs, horses, pigs, and even whales and dolphins. Influenza B virus is less virulent and is sometimes associated with epidemic outbreaks. Influenza C virus generally produces the mildest disease symptoms and is rarely connected with epidemics. Neither influenza B virus nor influenza C virus has significant animal reservoirs.

Table 23.5. The Three Major Groups of Influenza Viruses

Influenza A virus Influenza B virus Influenza C virus
Severity Severe Moderate Mild
Animal reservoir Yes No No
Genome segments 8 8 7
Population spread Epidemic and pandemic Epidemic Sporadic
Antigenic variation Shift/drift Drift Drift

Influenza virus infections elicit a strong immune response, particularly to the hemagglutinin protein, which would protect the individual if they encountered the same virus. Unfortunately, the antigenic properties of the virus change relatively rapidly, so new strains are evolving that immune systems previously challenged by influenza virus cannot recognize. When an influenza virus gains a new hemagglutinin or neuraminidase type, it is able to evade the host’s immune response and be successfully transmitted, often leading to an epidemic.

There are two mechanisms by which these evolutionary changes may occur. The mechanisms of antigen drift and antigenic shift for influenza virus have been described in Virulence Factors of Bacterial and Viral Pathogens. Of these two genetic processes, it is viruses produced by antigenic shift that have the potential to be extremely virulent because individuals previously infected by other strains are unlikely to produce any protective immune response against these novel variants.

The most lethal influenza pandemic in recorded history occurred from 1918 through 1919. Near the end of World War I, an antigenic shift involving the recombination of avian and human viruses is thought to have produced a new H1N1 virus. This strain rapidly spread worldwide and is commonly claimed to have killed as many as 40 million to 50 million people—more than double the number killed in the war. Although referred to as the Spanish flu, this disease is thought to have originated in the United States. Regardless of its source, the conditions of World War I greatly contributed to the spread of this disease. Crowding, poor sanitation, and rapid mobilization of large numbers of personnel and animals facilitated the dissemination of the new virus once it appeared.

Several of the most important influenza pandemics of modern times have been associated with antigenic shifts. A few of these are summarized in Table 23.6.[4][5][6]

Table 23.6. Historic Influenza Outbreaks

Historical Influenza Outbreaks
Years Common Name Serotype Estimated Number of Deaths
1918–1919 Spanish flu H1N1 20,000,000–40,000,000
1957–1958 Asian flu N2N2 1,000,000–2,000,000
1968–1969 Hong Kong flu H3N2 1,000,000–3,000,000
2009–2010 Swine flu H1N1/09 152,000–575,000

Laboratory diagnosis of influenza is typically performed using a variety of RIDTs. These tests are inoculated by point-of-care personnel and give results within 15–20 minutes. Unfortunately, these tests have variable sensitivity and commonly yield false-negative results. Other tests include hemagglutination of erythrocytes (due to hemagglutinin action) or complement fixation. Patient serum antibodies against influenza viruses can also be detected in blood samples. Because influenza is self-limiting disease, diagnosis through these more time-consuming and expensive methods is not typically used.

Three drugs that inhibit influenza neuraminidase activity are available: inhaled zanamivir, oral oseltamivir, and intravenous peramivir. If taken at the onset of symptoms, these drugs can shorten the course of the disease. These drugs are thought to impair the ability of the virus to efficiently exit infected host cells. A more effective means of controlling influenza outbreaks, though, is vaccination. Every year, new influenza vaccines are developed to be effective against the strains expected to be predominant. This is determined in February by a review of the dominant strains around the world from a network of reporting sites; their reports are used to generate a recommendation for the vaccine combination for the following winter in the northern hemisphere. In September, a similar recommendation is made for the winter in the southern hemisphere.[7] These recommendations are used by vaccine manufacturers to formulate each year’s vaccine. In most cases, three or four viruses are selected—the two most prevalent influenza A strains and one or two influenza B strains. The chosen strains are typically cultivated in eggs and used to produce either an inactivated or a live attenuated vaccine (e.g., FluMist). For individuals 18 years or older with an allergy to egg products, a recombinant egg-free trivalent vaccine is available. Most of the influenza vaccines over the past decade have had an effectiveness of about 50%.[8]

CASE IN POINT: Flu Pandemic

During the spring of 2013, a new strain of H7N9 influenza was reported in China. A total of 132 people were infected. Of those infected, 44 (33%) died. A genetic analysis of the virus suggested that this strain arose from the reassortment of three different influenza viruses: a domestic duck H7N3 virus, a wild bird H7N9 virus, and a domestic poultry H9N2 virus. The virus was detected in the Chinese domestic bird flocks and contact with this reservoir is thought to have been the primary source of infection. This strain of influenza was not able to spread from person to person. Therefore, the disease did not become a global problem. This case does, though, illustrate the potential threat that influenza still represents. If a strain like the H7N9 virus were to undergo another antigenic shift, it could become more communicable in the human population. With a mortality rate of 33%, such a pandemic would be disastrous. For this reason, organizations like the World Health Organization and the Centers for Disease Control and Prevention keep all known influenza outbreaks under constant surveillance.

  • Compare the severity of the three types of influenza viruses.
  • Why must new influenza vaccines be developed each year?

Viral Pneumonia

Viruses cause fewer cases of pneumonia than bacteria; however, several viruses can lead to pneumonia in children and the elderly. The most common sources of viral pneumonia are adenoviruses, influenza viruses, parainfluenza viruses, and respiratory syncytial viruses. The signs and symptoms produced by these viruses can range from mild cold-like symptoms to severe cases of pneumonia, depending on the virulence of the virus strain and the strength of the host defences of the infected individual. Occasionally, infections can result in otitis media.

Respiratory syncytial virus (RSV) infections are fairly common in infants; most people have been infected by the age of 2 years. During infection, a viral surface protein causes host cells to fuse and form multinucleated giant cells called syncytia. There are no specific antiviral therapies or vaccines available for viral pneumonia. In adults, these infections are self-limiting, resemble the common cold, and tend to resolve uneventfully within 1 or 2 weeks. Infections in infants, however, can be life-threatening. RSV is highly contagious and can be spread through respiratory droplets from coughing and sneezing. RSV can also survive for a long time on environmental surfaces and, thus, be transmitted indirectly via fomites.

  • Who is most likely to contract viral pneumonia?
  • What is the recommended treatment for viral pneumonia?

SARS and MERS

Severe acute respiratory syndrome (SARS) and Middle East respiratory syndrome (MERS) are two acute respiratory infections caused by coronaviruses. In both cases, these are thought to be zoonotic infections. Bats and civet cats are thought to have been the reservoirs for SARS; camels seem to be the reservoir for MERS.

SARS originated in southern China in the winter of 2002 and rapidly spread to 37 countries. Within about 1 year, more than 8,000 people experienced influenza-like symptoms and nearly 800 people died. The rapid spread and severity of these infections caused grave concern at the time. However, the outbreak was controlled in 2003 and no further cases of SARS have been recorded since 2004.[9] Signs and symptoms of SARS include high fever, headache, body aches, and cough, and most patients will develop pneumonia.

MERS was first reported in Saudi Arabia in 2013. Although some infected individuals will be asymptomatic or have mild cold-like symptoms, most will develop a high fever, aches, cough and a severe respiratory infection that can progress to pneumonia. As of 2015, over 1,300 people in 27 countries have been infected. About 500 people have died. There are no specific treatments for either MERS or SARS. In addition, no vaccines are currently available. Several recombinant vaccines, however, are being developed.

  • What is the cause of SARS?
  • What are the signs and symptoms of MERS?

Viral Respiratory Diseases Causing Skin Rashes

Measles, rubella (German measles), and chickenpox are three important viral diseases often associated with skin rashes. However, their symptoms are systemic, and because their portal of entry is the respiratory tract, they can be considered respiratory infections.

Measles (Rubeola)

The measles virus (MeV) causes the highly contagious disease measles, also known as rubeola, which is a major cause of childhood mortality worldwide. Although vaccination efforts have greatly reduced the incidence of measles in much of the world, epidemics are still common in unvaccinated populations in certain countries.[10]

The measles virus is a single-stranded, negative-strand RNA virus and, like the influenza virus, it possesses an envelope with spikes of embedded hemagglutinin. The infection is spread by direct contact with infectious secretions or inhalation of airborne droplets spread by breathing, coughing, or sneezing. Measles is initially characterized by a high fever, conjunctivitis, and a sore throat. The virus then moves systemically through the bloodstream and causes a characteristic rash. The measles rash initially forms on the face and later spreads to the extremities. The red, raised macular rash will eventually become confluent and can last for several days. At the same time, extremely high fevers (higher than 40.6 °C [105 °F]) can occur. Another diagnostic sign of measles infections is Koplik’s spots, white spots that form on the inner lining of inflamed cheek tissues (Figure 23.16).

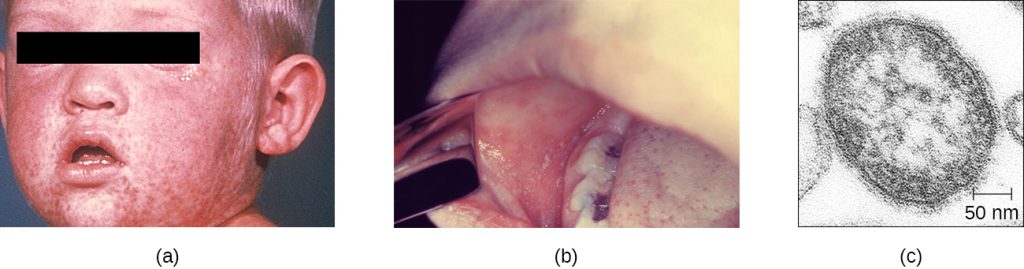
a) Red bumps on a child’s face. B) Red spots inside the mouth. c) A micrograph of an oval structure containing a scale bar measuring 50 nanometers.
Figure 23.16. (a) Measles typically presents as a raised macular rash that begins on the face and spreads to the extremities. (b) Koplik’s spots on the oral mucosa are also characteristic of measles. (c) A thin-section transmission electron micrograph of a measles virion. [Credit a, b, c: modification of work by Centers for Disease Control and Prevention]

Although measles is usually self-limiting, it can lead to pneumonia, encephalitis, and death. In addition, the inhibition of immune system cells by the measles virus predisposes patients to secondary infections. In severe infections with highly virulent strains, measles fatality rates can be as high as 10% to 15%. There were more than 145,000 measles deaths (mostly young children) worldwide in 2013.[11]

The preliminary diagnosis of measles is typically based on the appearance of the rash and Koplik’s spots. Hemagglutination inhibition tests and serological tests may be used to confirm measles infections in low-prevalence settings.

There are no effective treatments for measles. Vaccination is widespread in developed countries as part of the measles, mumps, and rubella (MMR) vaccine. As a result, there are typically fewer than 200 cases of measles in the United States annually.[12] When it is seen, it is often associated with children who have not been vaccinated.

MICRO CONNECTIONS: Preventable Measles Outbreaks

In December 2014, a measles epidemic began at Disneyland in southern California. Within just 4 months, this outbreak affected 134 people in 24 states.[13] Characterization of the virus suggests that an unidentified infected individual brought the disease to the United States from the Philippines, where a similar virus had sickened more than 58,000 people and killed 110.[14] Measles is highly communicable, and its spread at Disneyland may have been facilitated by the low vaccination rate in some communities in California.[15]

Several factors could conceivably lead to a strong comeback of measles in the U.S. Measles is still an epidemic disease in many locations worldwide. Air travel enables infected individuals to rapidly translocate these infections globally. Compounding this problem, low vaccination rates in some local areas in the United States (such as in Amish communities) provide populations of susceptible hosts for the virus to establish itself. Finally, measles has been a low-prevalence infection in the U.S. for some time. As a consequence, physicians are not as likely to recognize the initial symptoms and make accurate diagnoses. Until vaccination rates become high enough to ensure herd immunity, measles is likely to be an ongoing problem in the United States.

Rubella (German Measles)

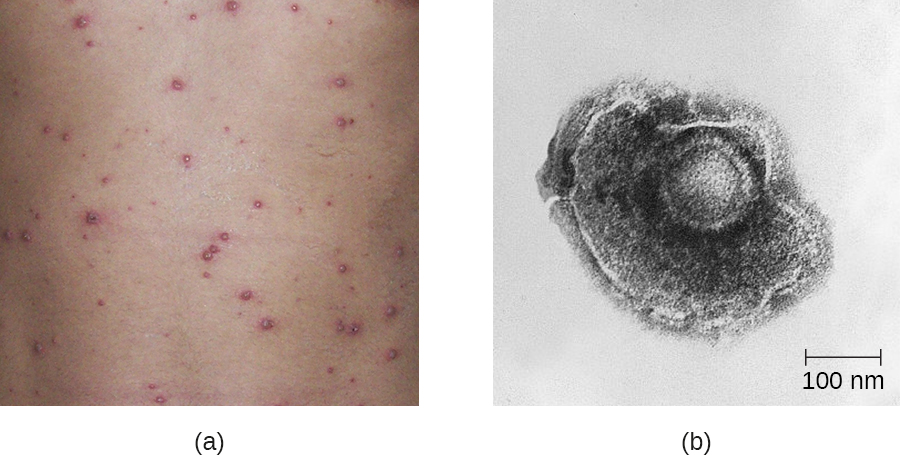
Rubella, or the German measles, is a relatively mild viral disease that produces a rash somewhat like that caused by the measles, even though the two diseases are unrelated. The rubella virus is an enveloped RNA virus that can be found in the respiratory tract. It is transmitted from person to person in aerosols produced by coughing or sneezing. Nearly half of all infected people remain asymptomatic. However, the virus is shed and spread by asymptomatic carriers. Like rubeola, rubella begins with a facial rash that spreads to the extremities (Figure 23.17). However, the rash is less intense, shorter lived (2–3 days), not associated with Koplik’s spots, and the resulting fever is lower (101 °F [38.3 °C]).

Congenital rubella syndrome is the most severe clinical complication of the German measles. This occurs if a woman is infected with rubella during pregnancy. The rubella virus is teratogenic, meaning it can cause developmental defects if it crosses the placenta during pregnancy. There is a very high incidence of stillbirth, spontaneous abortion, or congenital birth defects if the mother is infected before 11 weeks of pregnancy and 35% if she is infected between weeks 13–16; after this time the incidence is low.[16] For this reason, prenatal screening for rubella is commonly practiced in the United States. Postnatal infections are usually self-limiting and rarely cause severe complications.

Like measles, the preliminary diagnosis of rubella is based on the patient’s history, vaccination records, and the appearance of the rash. The diagnosis can be confirmed by hemagglutinin inhibition assays and a variety of other immunological techniques. There are no antiviral therapies for rubella, but an effective vaccine (MMR) is widely available. Vaccination efforts have essentially eliminated rubella in the United States; fewer than a dozen cases are reported in a typical year.

a) red bumps on a person's back. b) a micrograph of rubella.
Figure 23.17. (a) This photograph shows the appearance of the German measles (rubella) rash. Note that this is less intense than the rash of measles and the lesions are not confluent. (b) This transmission electron micrograph shows rubella virus virions just budding from a host cell. [Credit a, b: modification of work by Centers for Disease Control and Prevention]

Chickenpox and Shingles

Chickenpox, also known as varicella, was once a common viral childhood disease. The causative agent of chickenpox, the varicella-zoster virus, is a member of the herpesvirus family. In children, the disease is mild and self-limiting, and is easily transmitted by direct contact or inhalation of material from the skin lesions. In adults, however, chickenpox infections can be much more severe and can lead to pneumonia and birth defects in the case of infected pregnant women. Reye syndrome, mentioned earlier in this chapter, is also a serious complication associated with chickenpox, generally in children.

Once infected, most individuals acquire a lifetime immunity to future chickenpox outbreaks. For this reason, parents once held “chickenpox parties” for their children. At these events, uninfected children were intentionally exposed to an infected individual so they would contract the disease earlier in life, when the incidence of complications is very low, rather than risk a more severe infection later.

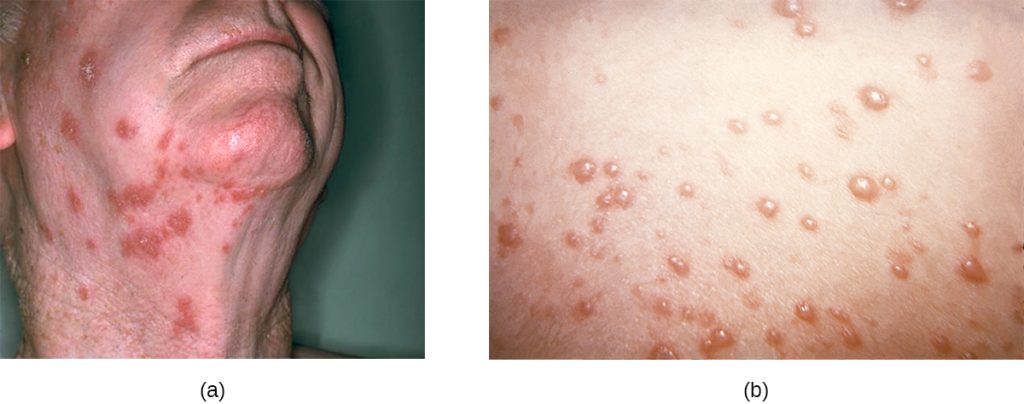
After the initial viral exposure, chickenpox has an incubation period of about 2 weeks. The initial infection of the respiratory tract leads to viraemia and eventually produces fever and chills. A pustular rash then develops on the face, progresses to the trunk, and then the extremities, although most form on the trunk (Figure 23.18). Eventually, the lesions burst and form a crusty scab. Individuals with chickenpox are infectious from about 2 days before the outbreak of the rash until all the lesions have scabbed over.

a) red bumps on skin. b) a micrograph of human herpesvirus 3 is shown. The diameter is approximately 300 nanometers according to a scale bar on the bottom right of the micrograph.
Figure 23.18. (a) The characteristic appearance of the pustular chickenpox rash is concentrated on the trunk region. (b) This transmission electron micrograph shows a viroid of human herpesvirus 3, the virus that causes chickenpox in children and shingles when it is reactivated in adults. [Credit b: modification of work by Centers for Disease Control and Prevention]

Like other herpesviruses, the varicella-zoster virus can become dormant in nerve cells. While the pustular vesicles are developing, the virus moves along sensory nerves to the dorsal ganglia in the spinal cord. Once there, the varicella-zoster virus can remain latent for decades. These dormant viruses may be reactivated later in life by a variety of stimuli, including stress, aging, and immunosuppression. Once reactivated, the virus moves along sensory nerves to the skin of the face or trunk. This results in the production of the painful lesions in a condition known as shingles (Figure 23.19). These symptoms generally last for 2–6 weeks, and may recur more than once. Post-herpetic neuralgia, pain signals sent from damaged nerves long after the other symptoms have subsided, is also possible. In addition, the virus can spread to other organs in immunocompromised individuals. A person with shingles lesions can transmit the virus to a non-immune contact, and the newly infected individual would develop chickenpox as the primary infection. Shingles cannot be transmitted from one person to another.

The primary diagnosis of chickenpox in children is mainly based on the presentation of a pustular rash of the trunk. Serological and PCR-based tests are available to confirm the initial diagnosis. Treatment for chickenpox infections in children is usually not required. In patients with shingles, acyclovir treatment can often reduce the severity and length of symptoms, and diminish the risk of post-herpetic neuralgia. An effective vaccine is now available for chickenpox. A vaccine is also available for adults older than 60 years who were infected with chickenpox in their youth. This vaccine reduces the likelihood of a shingles outbreak by boosting the immune defences that are keeping the latent infection in check and preventing reactivation.

a) Large red spots on an adult’s neck. B) Red bumps on skin.
Figure 23.19. (a) An individual suffering from shingles. (b) The rash is formed because of the reactivation of a varicella-zoster infection that was initially contracted in childhood. [Credit a: modification of work by National Institute of Allergy and Infectious Diseases (NIAID); credit b: modification of work by Centers for Disease Control and Prevention]
  • Why does measles often lead to secondary infections?
  • What signs or symptoms would distinguish rubella and measles?
  • Why can chickenpox lead to shingles later in life?

EYE ON ETHICS: Smallpox Stockpiles

Smallpox has probably killed more humans than any other infectious disease, with the possible exception of tuberculosis. This disease, caused by the variola major virus, is transmitted by inhalation of viral particles shed from lesions in the throat. The smallpox virus spreads systemically in the bloodstream and produces a pustular skin rash. Historical epidemics of smallpox had fatality rates of 50% or greater in susceptible populations. Concerted worldwide vaccination efforts eradicated smallpox from the general population in 1977. This was the first microbial disease in history to be eradicated, a feat made possible by the fact that the only reservoir for the smallpox virus is infected humans.

Although the virus is no longer present in the wild, laboratory samples of the virus still exist in the United States and Russia.[17] The question is, why do these samples still exist? Some claim that these stocks should be maintained for research purposes. Should the smallpox virus ever reappear, they say, we would need access to such stocks for development of vaccines and treatments. Concerns about a re-emergence of the virus are not totally unfounded. Although there are no living reservoirs of the virus, there is always the possibility that smallpox could re-emerge from mummified human bodies or human remains preserved in permafrost. It is also possible that there are as-yet undiscovered samples of the virus in other locations around the world. An example of such “lost” samples was discovered in a drawer in a Food and Drug Administration lab in Maryland.[18] If an outbreak from such a source were to occur, it could lead to uncontrolled epidemics, since the population is largely unvaccinated now.

Critics of this argument, including many research scientists and the World Health Organization, claim that there is no longer any rational argument for keeping the samples. They view the “re-emergence scenarios” as a thinly veiled pretence for harbouring biological weapons. These scenarios, they say, are less probable than an intentional reintroduction of the virus from militarized stocks by humans. Furthermore, they point out that if we needed to research smallpox in the future, we could rebuild the virus from its DNA sequence.

What do you think? Are there legitimate arguments for maintaining stockpiles of smallpox, or should all forms of this deadly disease be eradicated?

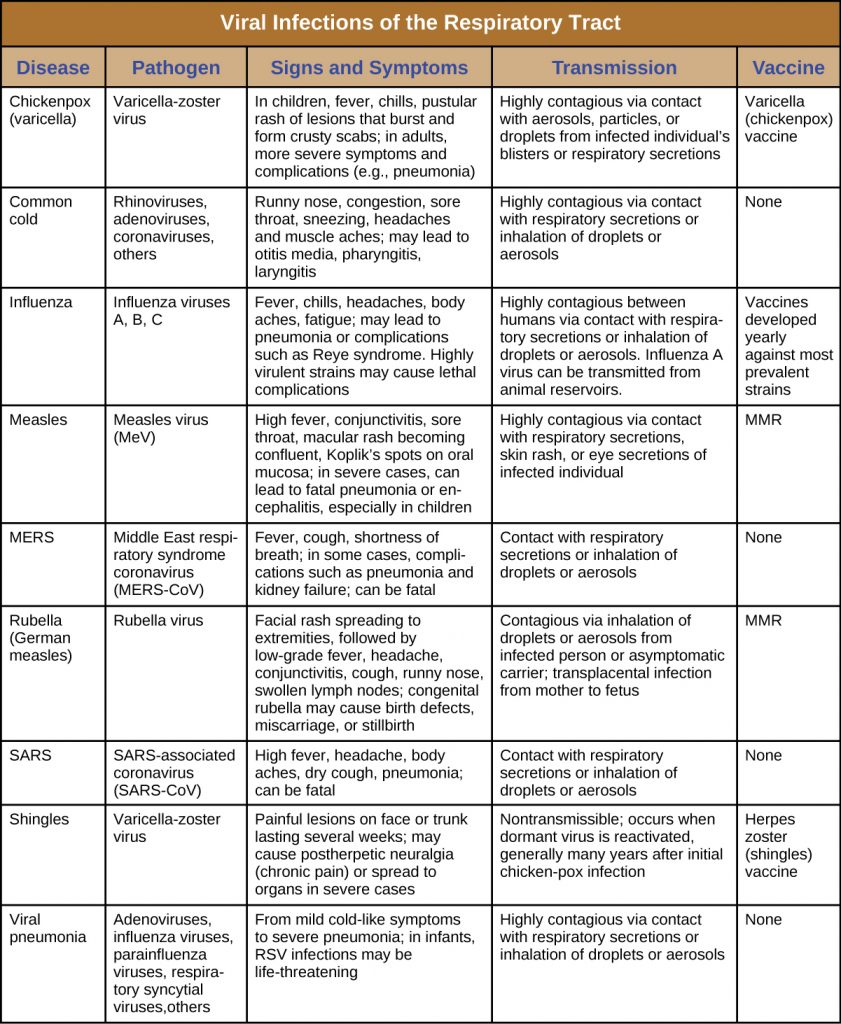
DISEASE PROFILES: Viral Infections of the Respiratory Tract

Many viruses are capable of entering and causing disease in the respiratory system, and a number are able to spread beyond the respiratory system to cause systemic infections. Most of these infections are highly contagious and, with a few exceptions, antimicrobial drugs are not effective for treatment. Although some of these infections are self-limiting, others can have serious or fatal complications. Effective vaccines have been developed for several of these diseases, as summarized in Table 23.7.

Table 23.7. Viral Infections of the Respiratory Tract

Table summarizing viral infecions of the respiratory tract including the pathogen, signs and symptoms, mode of transmission and if there's a vaccine

Key Takeaways

  • Viruses cause respiratory tract infections more frequently than bacteria, and most viral infections lead to mild symptoms.
  • The common cold can be caused by more than 200 viruses, typically rhinoviruses, coronaviruses, and adenoviruses, transmitted by direct contact, aerosols, or environmental surfaces.
  • Due to its ability to rapidly mutate through antigenic drift and antigenic shift, influenza remains an important threat to human health. Two new influenza vaccines are developed annually.
  • Several viral infections, including respiratory syncytial virus infections, which frequently occur in the very young, can begin with mild symptoms before progressing to viral pneumonia.
  • SARS and MERS are acute respiratory infections caused by coronaviruses, and both appear to originate in animals. SARS has not been seen in the human population since 2004 but had a high mortality rate during its outbreak. MERS also has a high mortality rate and continues to appear in human populations.
  • Measles, rubella, and chickenpox are highly contagious, systemic infections that gain entry through the respiratory system and cause rashes and fevers. Vaccines are available for all three. Measles is the most severe of the three and is responsible for significant mortality around the world. Chickenpox typically causes mild infections in children but the virus can reactivate to cause painful cases of shingles later in life.

Multiple Choice

Fill in the Blank

Short Answer

  1. Since we all have experienced many colds in our lifetime, why are we not resistant to future infections?

Critical Thinking

  1. What role does the common cold have in the rise of antibiotic-resistant strains of bacteria in the United States?
  2. Why is it highly unlikely that influenza A virus will ever be eradicated, like the smallpox virus?

 

Media Attributions

  • OSC_Microbio_22_03_Influenza
  • OSC_Microbio_22_03_Measles
  • Print
  • OSC_Microbio_22_03_Chicken
  • OSC_Microbio_22_03_Shingles
  1. AG L’Huillier et al. “Survival of Rhinoviruses on Human Fingers.” Clinical Microbiology and Infection 21, no. 4 (2015):381–385. ↵
  2. Centers for Disease Control and Prevention. “Estimating Seasonal Influenza-Associated Deaths in the United States: CDC Study Confirms Variability of Flu.” 2016. http://www.cdc.gov/flu/about/disease/us_flu-related_deaths.htm. Accessed May 14, 2019. ↵
  3. ED Belay et al. “Reye’s Syndrome in the United States From 1981 Through 1997.” New England Journal of Medicine 340 no. 18 (1999):1377–1382. ↵
  4. CE Mills et al. “Transmissibility of 1918 Pandemic Influenza.” Nature 432, no. 7019 (2004):904–906. ↵
  5. E. Tognotti. “Influenza Pandemics: A Historical Retrospect.” Journal of Infection in Developing Countries 3, no. 5 (2009):331–334. ↵
  6. FS Dawood et al. “Estimated Global Mortality Associated with the First 12 Months of 2009 Pandemic Influenza A H1N1 Virus Circulation: A Modelling Study.” The Lancet Infectious Diseases 12, no. 9 (2012):687–695. ↵
  7. World Health Organization. “WHO Report on Global Surveillance of Epidemic-Prone Infectious Diseases.” 2000. http://www.who.int/csr/resources/publications/surveillance/Influenza.pdf. Accessed May 2014, 2019. ↵
  8. Centers of Disease Control and Prevention. “Vaccine Effectiveness - How Well Does the Flu Vaccine Work?” 2016. http://www.cdc.gov/flu/about/qa/vaccineeffect.htm. Accessed May 14, 2019. ↵
  9. Y. Huang. “The SARS Epidemic and Its Aftermath in China: A Political Perspective.” In Learning from SARS: Preparing for the Next Disease Outbreak. Edited by S. Knobler et al. Washington, DC: National Academies Press; 2004. Available at: http://www.ncbi.nlm.nih.gov/books/NBK92479/ ↵
  10. Centers for Disease Control and Prevention. “Global Health - Measles, Rubella, and CRS, Eliminating Measles, Rubella & Congenital Rubella Syndrome (CRS) Worldwide.” 2015. http://www.cdc.gov/globalhealth/measles/. AccessedMay 14, 2019. ↵
  11. World Health Organization. “Measles Factsheet.” 2016. http://www.who.int/mediacentre/factsheets/fs286/en/. Accessed May 14, 2019. ↵
  12. Centers for Disease Control and Prevention. “Measles Cases and Outbreaks.” 2016. http://www.cdc.gov/measles/cases-outbreaks.html. Accessed May 14, 2019. ↵
  13. Ibid ↵
  14. World Health Organization. “Measles-Rubella Bulletin.” Manila, Philippines; Expanded Programme on Immunization Regional Office for the Western Pacific World Health Organization; 9 no. 1 (2015). http://www.wpro.who.int/immunization/documents/mrbulletinvol9issue1.pdf ↵
  15. M. Bloch et al. “Vaccination Rates for Every Kindergartener in California.” The New York Times February 6, 2015. http://www.nytimes.com/interactive/2015/02/06/us/california-measles-vaccines-map.html?_r=1. Accessed May 14, 2019. ↵
  16. E. Miller et al. “Consequences of Confirmed Maternal Rubella at Successive Stages of Pregnancy.” The Lancet 320, no. 8302 (1982):781–784. ↵
  17. Centers for Disease Control and Prevention. “CDC Media Statement on Newly Discovered Smallpox Specimens.” July 8, 2014. http://www.cdc.gov/media/releases/2014/s0708-nih.html. Accessed on May 14, 2019. ↵
  18. Ibid. ↵

License

Icon for the Creative Commons Attribution 4.0 International License

Microbiology: Canadian Edition Copyright © 2019 by Wendy Keenleyside is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book