Chapter 10

(Note: in 2023, only 6 months depreciation can be recorded, as the asset has reached the end of its useful life.)

---

Exercise 10.3

1. No journal entry is required as this is considered a change in estimate. Depreciation will be adjusted prospectively only, with no adjustment made to prior years.

2. Original depreciation:

   ($39,000 − $4,000) 5 years = $7,000 per year

   Depreciation taken 2018-2020 = $7,000 × 3 years = $21,000

   Revised depreciation for 2021 and future years:

   ($39,000 − $21,000 − $5,000) ÷ (7 years − 3 years = 4) = $3,250 per year

   

---

Exercise 10.4

1. Depreciation from 2006 – 2011:

   ($450,000 − $90,000) ÷ 30 years = $12,000 per year

   Total depreciation taken = $12,000 × 6 years = $72,000

2. Depreciation from 2012 – 2019:

   ($450,000 − $72,000 + $30,000 − $50,000) ÷ (30 − 6 + 10 = 34 years) = $10,529 per year

   Total depreciation taken = $10,529 × 8 years = $84,232

3. Depreciation from 2020 and future years:

   ($450,000 + $30,000 − $72,000 − $84,232) ÷ (34 − 8 = 26 years) = $12,453 per year

---

Exercise 10.5

1. Determine the recoverable amount:

   Value in use

   Fair value in use

   = $110,000

   = $116,000

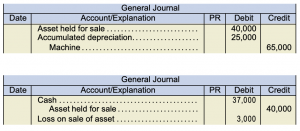
   The recoverable amount is the greater amount: $116,000

   Carrying value = $325,000 − $175,000 = $150,00

   As the carrying value exceeds the recoverable amount, the asset is impaired by $150,000 − $116,000 = $34,000

2. 

3. New carrying value = $150,000 − $34,000 = $116,000

   Depreciation = ($116,000 − 0) ÷ 3 years = $38,667

   

4. Determine the recoverable amount:

   Value in use

   Fair value less costs to sell

   $90,000

   $111,000

   The recoverable amount is the greater amount: $111,000

   The carrying value is now $116,000 − $38,667 = $77,333

   The asset is no longer impaired. However, the reversal of the impairment loss is limited. If the impairment had never occurred, the carrying value of the asset would have been:

   Unimpaired carrying value on Jan 1, 2021

   Depreciation for 2021 (150,000 ÷ 3)

   Unimpaired carrying value at Dec 31, 2021

   $ 150,000

   (50,000)

   100,000

   Therefore, the reversal of the impairment loss is limited to: $100,000 − $77,333 = $22,667

   The journal entry will be:

   

---

Exercise 10.6

1. ASPE 3063 uses a two-step process for determining impairment losses. The first step is to determine if the asset is impaired by comparing the undiscounted future cash flows to the carrying value:

   Undiscounted future cash flows:

   Carrying value

   $140,000

   $150,000

   Therefore, the asset is impaired.

   The second step is to determine the amount of the impairment. This amount is the difference between the carrying value and the fair value of the asset:

   Carrying value

   Fair value

   Impairment loss

   $150,000

   $125,000

   $ 25,000

   Thus, the journal entry will be:

   

2. Depreciation will now be based on the new carrying value:

   $150,000 − $25,000 = $125,000

   $125,000 ÷ 3 years  = $41,667 per year

   

3. The carrying value is now $125,000 − $41,667 = $83,333. As this is less than the undiscounted future cash flows, the asset is no longer impaired. However, under ASPE 3063, reversals of impairment losses are not allowed, so no adjustment can be made in this case.

---

Exercise 10.7

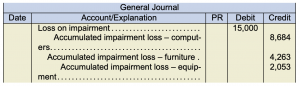
1. The total carrying value of the division is $95,000. The fair values of the individual assets cannot be determined, so the value in use is the appropriate measure. In this case, the value in use is $80,000, which means the division is impaired by $15,000. This impairment will be allocated on a pro-rata basis to the individual assets:
   

   Asset	Carrying Amount	Proportion	Impairment
   Computers	$55,000	55/95	$8,684
   Furniture	27,000	27/95	4,263
   Equipment	13,000	13/95	2,053
   	95,000		15,000

2. The journal entry would be:
3. The value in use ($80,000) is greater than the fair value less costs to sell ($60,000) so the calculation of impairment loss is the same as in part (a) (i.e., $15,000). However, none of the impairment loss should be allocated to the computers, as their carrying value ($55,000) is less than their recoverable amount ($60,000). The impairment loss would therefore be allocated as follows:
   

   Asset	Carrying Amount	Proportion	Impairment Loss
   Furniture	$27,000	27/40	$10,125
   Equipment	13,000	13/40	4,875
   	40,000		15,000

4. The impairment loss is still calculated as $15,000. However, this time the computers are also impaired, as their carrying value ($55,000) is greater than their recoverable amount ($50,000). In this case, the computers are reduced to their recoverable amount and the remaining impairment loss ($15,000 − $5,000 = $10,000) is allocated to the furniture and equipment on a pro-rata basis:
   

   Asset	Carrying Amount	Proportion	Impairment Loss
   Computers	$55,000		$5,000
   Furniture	27,000	27/40	6,750
   Equipment	13,000	13/40	3,250
   	95,000		15,000

---

Exercise 10.8

1. 
2. 
3. 
4. 

---

Exercise 10.9

1. 
2. 
3. 

---

Exercise 10.10

Undiscounted cash flow (UDCF)		$355,000
Carrying value		$408,700	($654,600 - $245,900)
Since UDCF < Carrying value, the is impairment.
To determine impairment, compare the carrying value to the fair value
Fair value		$395,600
Carrying value		$408,700
Loss due to impairement is $13,100 ($408,700 - $395,600)
Loss on impairment			13,100
	Accumulated impairment loss - equipment			13,100

---

Exercise 10.11

1. Hanover follows ASPE – Cost recovery impairment model

a. Compare the undiscounted cash flow to the carrying value:

	Undiscounted cash flow (UDCF)		7,695,000
	Carrying value ($11,500,000 - $3,500,000)		8,000,000
	Since UDCF < Carrying value, there is impairment
	To calculate the amount of impairment, compare fair value to carrying value
	Fair value	6,200,000
	Carrying value	8,000,000
	Impairment = $1,800,000 ($8,000,000 - $6,200,000)
Dec 31, Y4	Loss on impairment			1,800,000
		Accumulated impairment loss - equipment			1,800,000

b. Depreciation expense (straight-line)

	New value of equipment		6,200,000
	remaining useful life		4	years
	Annual depreciation		1,550,000
Dec 31, Y5	Depreciation expense			1,550,000
		Accumulated depreciation - equipment			1,550,000

c. No entry allowed! Under the cost recovery impairment model (ASPE), recovery of any impairment loss is NOT permitted.

2. Hanover follows IFRS – Rational entity impairment model

a. Determine the recoverable amount and compare that value to the carrying value:

	Carrying value			8,000,000
	Recoverable amount (higher of):
		Value in use	6,350,000
		Fair value less costs to sell	6,110,500
	Therefore, recoverable amount is			6,350,000
	Impairment			1,650,000
Dec 31, Y4	Loss on impairment				1,650,000
		Accumulated impairment loss - equipment				1,650,000

b. Depreciation expense (straight-line)

	New value of equipment		6,350,000
	remaining useful life		4	years
	Annual depreciation		1,587,500
Dec 31, Y5	Depreciation expense			1,587,500
		Accumulated depreciation - equipment			1,587,500

c. Recovery of impairment is allowed under IFRS but there is a maximum amount.

Carrying value of equipment (at Dec 31, Y5)		4,762,500
Fair value of equipment (at Dec 31, Y5)		6,500,000
Potential recovery is $1,737,500 ($6,500,000 - $4,762,500)
However, we have to check what the carrying value would have been WITHOUT impairment:
Original carrying value ($11,500,000 - $3,500,000)		8,000,000
Y5 depreciation ($8,000,000 / 4 years)		2,000,000
Carrying value at end of Y5		$6,000,000	MAXIMUM AMOUNT
The maximum amount we can recover is up to $6,000,000, not the $6,500,000 fair value
Maximum recovery:
Carrying value of equipment (at Dec 31, Y5)		4,762,500
Carrying value of equipment (if no impairment)		6,000,000
Recovery is $1,237,500 ($6,000,000 - $4,762,500)
Accumulated impairment loss - equipment			1,237,500
	Recovery of loss from impairment			1,237,500

---

Exercise 10.12

1. Goderich follows APSE – Cost recovery impairment model

a. Compare the undiscounted cash flow to the carrying value:

	Undiscounted cash flow (UDCF)		295,300
	Carrying value ($529,600 - 224,200)		305,400
	Since UDCF < Carrying value, there is impairment
	To calculate the amount of impairment, compare fair value to carrying value
	Fair value		245,600
	Carrying value		305,400
	Impairment = $9,800 ($305,400 - 295,600)
Dec 31, Y4	Loss on impairment			59,800
		Accumulated impairment loss - equipment			59,800

b. Depreciation expense (straight-line)

	New value of equipment	245,600
	remaining useful life	5	years
	Annual depreciation	49,120
Dec 31, Y5	Depreciation expense		49,120
	Accumulated depreciation - equipment			49,120

c. No entry allowed! Under the cost recovery impairment model (ASPE), recovery of any impairment loss is NOT permitted.

2. Goderich follows IFRS – Rational entity impairment model

a. Determine the recoverable amount and compare that value to the carrying value:

	Carrying value			305,400
	Recoverable amount (higher of):
		Value in use	296,500
		Fair value less costs to sell	245,600
	Therefore, recoverable amount is			296,500
	Impairment			8,900
Dec 31, Y4	Loss on impairment				8,900
		Accumulated impairment loss - equipment				8,900

b. Depreciation expense (straight-line)

	New value of equipment		296,500
	remaining useful life		5	years
	Annual depreciation		59,300
Dec 31, Y5	Depreciation expense			59,300
		Accumulated depreciation - equipment			59,300

c. Recovery of impairment is allowed under IFRS but there is a maximum amount.

Carrying value of equipment (at Dec 31, Y5)		237,200
Fair value of equipment (at Dec 31, Y5)		305,100
Potential recovery is $82,725 ($305,100 - $222,375)
However, we have to check what the carrying value would have been WITHOUT impairment:
Original carrying value ($529,600 - $224,200)		305,400
Y5 depreciation ($305,400 / 5 years)		61,080
Carrying value at end of Y5		$244,320	MAXIMUM AMOUNT
The maximum amount we can recover is up to $244,320, not the $305,100 fair value
Maximum recovery:
Carrying value of equipment (at Dec 31, Y5)		237,200
Carrying value of equipment (if no impairment)		244,320
Recovery is $7,120 ($244,320 - $237,200)
Accumulated impairment loss - equipment			7,120
	Recovery of loss from impairment			7,120

---

Exercise 10.13

1. Straight-line method

Y8	$256,000 - $16,000 10 years	=	20,000	× 9/12 =	$15,000
Y9	$256,000 - $16,000 10 years	=			$20,000

2. Units-of-production method

	$256,000 - $16,000 125,000 units	=	$1.60	rate per unit
Y8	9,860 units × $1.60	=			$15,776
Y9	11,400 units × $1.60	=			$18,240

3. Double-declining balance method

	1/10 × 2 = .10 × 2 = 20% annual rate
Y8	$256,000 × 20% × 9/12 =	$38,400
Y9	($256,000 - $38,400) × 20% =	$43,520

---

Exercise 10.14

1. Straight-line method

			Depreciation Expense	Accumulated Depreciation
Y3	$345,000 - $34,700 8 years	=	$38,875	$38,875
Y4	$345,000 - $34,700 8 years	=	$38,875	$77,750

2. Unit-of-Production

					Depreciation Expense	Accumulated Depreciation
	$345,000 - $34,700 31,100 units	=	$10.00	rate
Y3	3,890 units x $10.00 rate per unit =				$38,900	$38,900
Y4	3,560 units x $10.00 rate per unit =				$35,600	$74,500