6.7 Measuring Productivity

An economy’s rate of productivity growth is closely linked to the growth rate of its GDP per capita, although the two are not identical. For example, if the percentage of the population who holds jobs in an economy increases, GDP per capita will increase, but the productivity of individual workers may not be affected. Over the long term, the only way that GDP per capita can grow continually is if the average worker’s productivity rises or if there are complementary increases in capital. A common measure of Canadian productivity per worker is the dollar value per hour the worker contributes to the employer’s output. The link below provides further information on changes to labour productivity for Canadian businesses. It discusses the changes across certain sectors, such as manufacturing, oil and gas, and mining, to name a few.

“Before the 2008 recession hit, the overriding concern for the Canadian macroeconomy was our poor record of productivity growth . . . When we talk about the importance of productivity, the point is invariably made that increasing output per worker is the only sustainable way of generating long-run gains in real purchasing power” (Gordon, 2010). Meanwhile, output per worker in the US has been growing almost twice as fast.

Technology and Productivity

If the economy’s growth depended only on the deepening of human capital and physical capital, then we would expect that economy’s growth rate to slow down over the long run because of diminishing marginal returns. However, another crucial factor in the aggregate production function is technology.

Developing new technology can provide a way for an economy to sidestep the diminishing marginal returns of capital deepening. Fig 6.7 below demonstrates that.

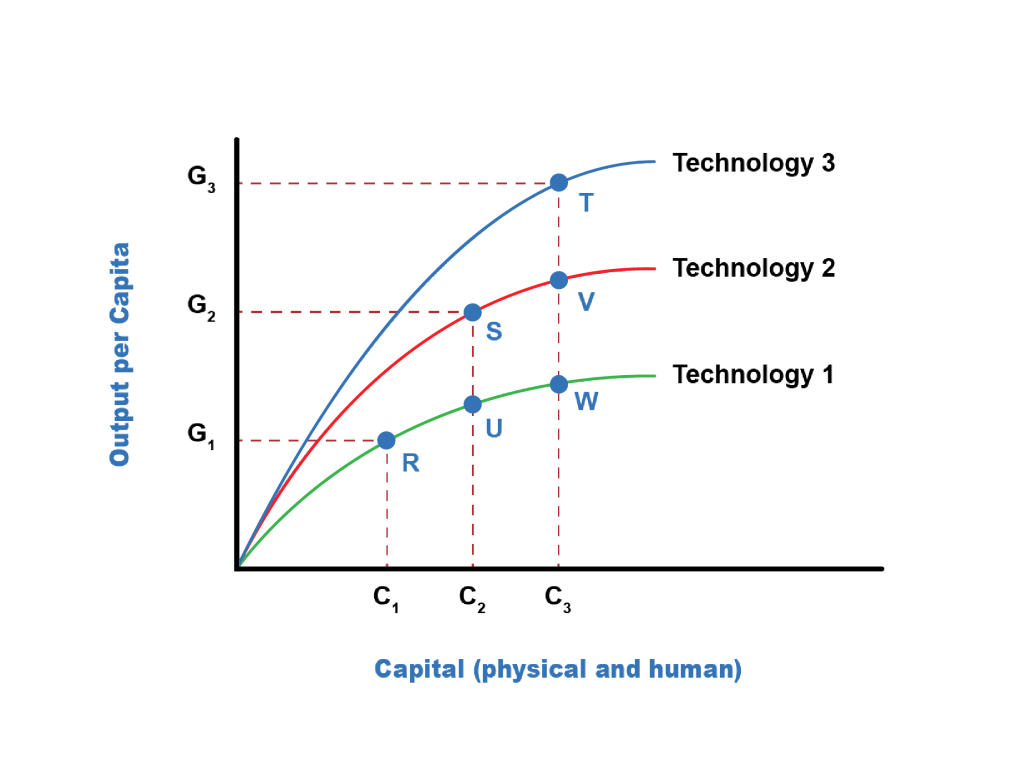
The horizontal axis measures the deepening of both physical and human capital. The amount of human and physical capital per worker increases as one moves from left to right, from C1 to C2 to C3—the vertical axis measures per capita output. We consider the lowest aggregate production function in this diagram, labelled Technology 1. Along this aggregate production function, the level of technology is held constant, so the line shows only the relationship between capital deepening and output. As capital deepens from C1 to C2 to C3 and the economy moves from R to U to W, per capita output does increase—but how the line starts out steeper on the left but then flattens as it moves to the right shows the diminishing marginal returns, as additional marginal amounts of capital deepening increase output by ever-smaller amounts. The shape of the aggregate production line (Technology 1) shows that the ability of capital deepening to generate sustained economic growth is limited since diminishing returns will eventually set in.

Now, let us consider improvements in technology. Improved technology means that more output is possible with a given set of inputs. The production function labelled Technology 1 in the figure is based on one level of technology, but Technology 2 is based on an improved level of technology, so for every level of capital deepening, it produces a higher level of output on the vertical axis. In turn, production function Technology 3 represents a still higher level of technology so that for every level of inputs, it produces a higher output level than the other two aggregate production functions.

Most healthy, growing economies are deepening their human and physical capital and increasing technology simultaneously. As a result, the economy can move from a choice like point R on the Technology 1 aggregate production line to a point like S on Technology 2 and a point like T on the still higher aggregate production line (Technology 3). With the combination of technology and capital deepening, the rise in GDP per capita does not need to fade away because of diminishing returns. The gains from technology can offset the diminishing returns involved with capital deepening.