6.5 The “Rule of 70” and Differences in Growth Rates

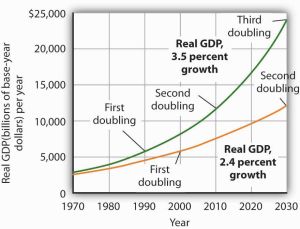
Suppose two economies with equal populations start at the same level of real GDP but grow at different rates. Economy A grows at a rate of 3.5%, and Economy B grows at a rate of 2.4%. In how many years will each of the two economies double in size? If the GDP of Economy A is $1.3 trillion in 2019, in how many years will the real GDP grow to $2.6 at its current growth rate of 3.5%? Similarly, if the GDP of Economy B is $1.3 trillion in 2019, in how many years will the real GDP grow to $2.6, at its current growth rate of 2.4%?

The doubling time is given by the Rule of 70, which states that a variable’s approximate doubling time equals 70 divided by the growth rate, stated as a whole number. If the level of income were increasing at a 9% rate, for example, its doubling time would be roughly 70 ÷ 9, or 7.7 years.

So, given the Rule of 70, Economy A would double in size in [latex]\frac{70}{3.5}=20[/latex] years, and Economy B would double in [latex]\frac{70}{2.4}=29[/latex] years. The Rule of 70 gives an approximation of exponential growth’s impact, not an exact measure.