Solutions
Chapitre 1 – La stœchiométrie
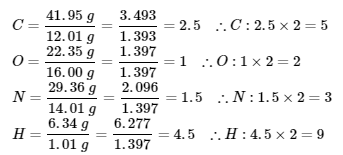
∴ the empirical formula of the unknown gas is C5O2N3H9
(1) Équilibrage :
MnO4– (aq) → Mn2+ (aq)
MnO4– (aq) → Mn2+ (aq) + 4 H2O
MnO4– (aq) + 8 H+ → Mn2+ (aq) + 4 H2O
3 OH– + MnO4– (aq) + 8 H+ → Mn2+ (aq) + 4 H2O + 8 OH–
8 H2O + MnO4– (aq) → Mn2+ (aq) + 4 H2O + 8 OH–
4 H2O + MnO4– (aq) → Mn2+ (aq) + 8 OH–
4 H2O + MnO4– (aq) + 5 e– → Mn2+ (aq) + 8 OH– (x 28)
(2) Équilibrage
C6H12O4 (aq) → 6 HCO3– (aq)
14 H2O + C6H12O4 (aq) → 6 HCO3– (aq)
14 H2O + C6H12O4 (aq) → 6 HCO3– (aq) + 34 H+
34 OH– + 14 H2O + C6H12O4 (aq) → 6 HCO3– (aq) + 34 H+ + 34 OH–
34 OH– + 14 H2O + C6H12O4 (aq) → 6 HCO3– (aq) + 34 H2O
34 OH– + C6H12O4 (aq) → 6 HCO3– (aq) + 20 H2O
34 OH– + C6H12O4 (aq) → 6 HCO3– (aq) + 20 H2O + 28 e– (x 5)
(3) Combinez les demi-équations pour la réponse finale :2 H2O + 28 MnO4– (aq) + 5 C6H12O4 (aq) 28 Mn2+ (aq) + 54 OH– + 30 HCO3– (aq)

4. Cl2 (g)
5. +2
6.
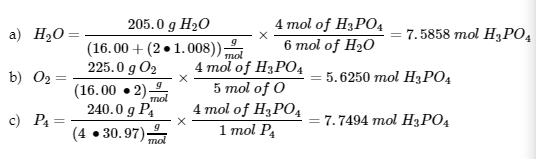
L’O2 est le réactif limitant
![]()
(2) La masse des réactifs excédentaires qui n’ont pas réagi :
Masse excédentaire = (205,0 + 225,0 + 240,0) g – 551,2 g = 118,8 g
7. 28,6 % en masse signifie qu’il y a 28,6 g de C2H6O2 dans 100 g de solution. La masse d’eau dans la solution est donc la différence entre ces valeurs :
|
|
C2H6O2 |
H2O |
SOLUTION |
|
Masse (g) |
28.6 |
71.4 |
100 |
|
Masse molaire (g/mol) |
62.07 |
|
|
|
Mol |
0.461 |
|
|
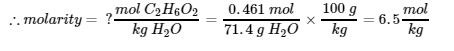
8.
2 e– + Pb2+ (aq) → Pb (s)
2 OH– (aq) + CN– (aq) → CNO– (aq) +H2O (l) + 2 e-
____________________________________________________
CN– (aq) + 2 OH– (aq) + Pb2+ (aq) → CNO– (aq) + H2O (l) + Pb (s)
Agent réducteur → CN–(aq) Agent oxydant → Pb2+(aq)
9. NO3–
10.
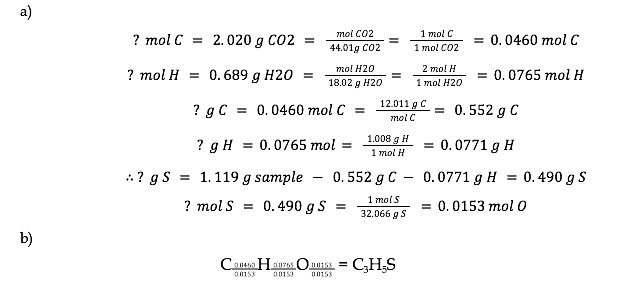
Chapitre 2 – Les gaz
- (1) Équation chimique équilibrée : C2H5OH (l) + 3 O2 (g) → 2 CO2 (g) + 3 H2O (l)
(2) Trouvez la masse de CO2 (g) :
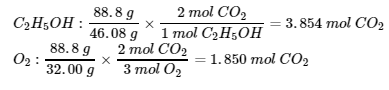
O2 est le réactif limite ∴ masse de CO2 = (1,850 mol)(44,01g/mol) = 81,4 g
(3)

(4)

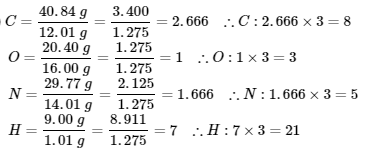
∴ la formule empirique du gaz inconnu est C8O3N5H21
(2)
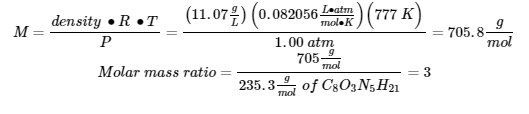
∴ la formule moléculaire du gaz inconnu est C24O9N15H63
3 (a)
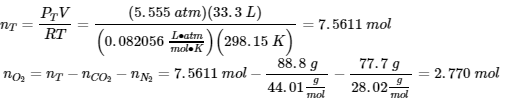
? mass O2 = (2.770 mol)(32.00 g/mol) = 88.7 g
(b)

4. (1)
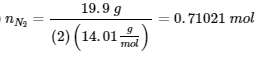
Trouvez la température initiale :

5. 0,020 mol/hr
6. Faux
7. (a)
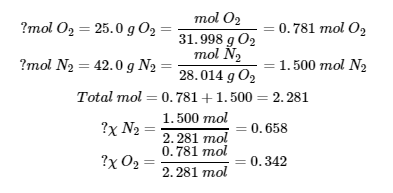
(b)
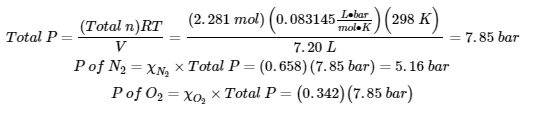
8.
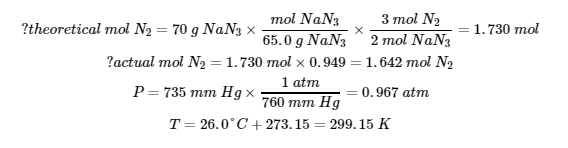
Chapitre 3 – La thermochimie
(1) calculer la valeur de q pour la combustion de 1,22 g de C6H10O(l) à volume constant (ce qui signifie que q = ∆U)
qreaction = ΔU = – qeau – qcal
qreaction = – mH2O∙c∙∆TH2O-(Ccal∙∆Tcal)
qreaction = -(2725 g)(4.188 J/g∙K)(2.75 K) – (3500 J/K)(2.75 K)
qreaction = – 40988 J
qreaction = – 40.988 kJ
Pour une mole, il y a 98,14 g
x = ΔU = – 3297 kJ
(2) maintenant, nous trouverons Q, W, ∆H et ∆U à pression constante. Mais ∆U est toujours à -3297 kJ
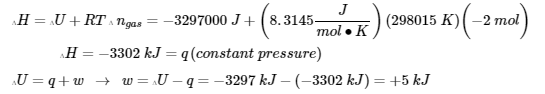
2 (a)

(b)
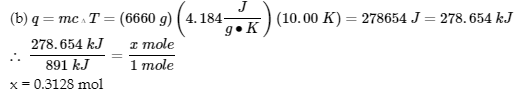

4. (1) Utiliser la loi de Hess :
C (graphite) + O2 (g) → CO2 (g) ΔH = – 393.5 kJ
2 H2 (g) + O2 (g) → 2 H2O (l) ΔH = 2(- 285.8 kJ) = – 571.6 kJ
CO2 (g) + 2 H2O (l) → CH3OH (l) + 32 O2 (g) ΔH = -(- 726.4 kJ) = +726.4 kJ
CH3OH (l) → CH3OH (g) ΔH= + 37.4 kJ
C (graphite) + 2 H2 (g) + 12 O2 (g) → CH3OH (g) ΔH = -201.3 kJ
(2)

5.
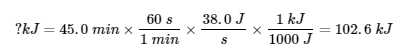
Techniquement, le signe ici devrait être négatif puisque la chaleur part, mais comme cela est déjà reconnu dans la question, ce n’est pas nécessaire.
7. (a)
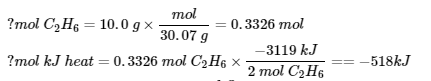
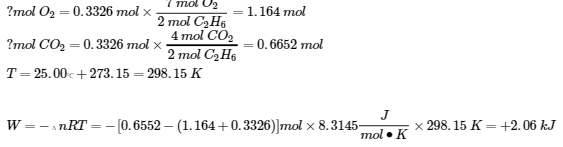
Chapitre 4 – Équilibre chimique
(a)
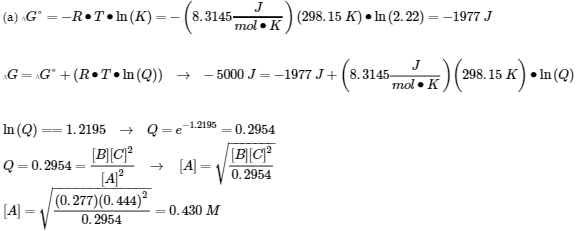
(b)
|
|
2 A (g) |
2 B (g) + |
C (g) |
|
I |
4.00 atm |
2.00 atm |
|
|
C |
-2x |
+ 2x |
+x |
|
E |
4.00 – 2x |
2.00 + 2x |
x |
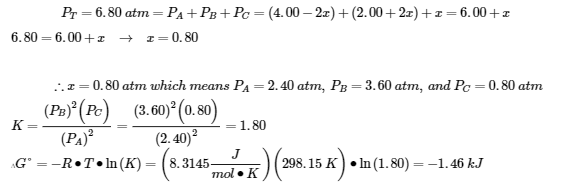
2.
![]()
|
|
A (aq) + |
B (aq) ⇌ |
2 C (aq) |
|
I |
0.322 M |
0.244 M |
0.455 M |
|
C |
-x |
-x |
+2x |
|
E |
0.322 – x |
0.244 – x |
0.455 + 2x |
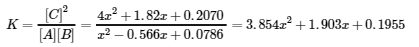
3.854x2+1.903x+0.1955=0 → x=-0.146 et-0.348
(notez que x est trouvé en utilisant la formule quadratique et que x = -0,348 est impossible)
[C] = 0.455 + 2x = 0455 + (2)(- 0.146) = 0.164 M
Notez que la masse molaire de AgNO3 est de 169,87 g/mol
![]()
|
|
Ag+ (aq) + |
2 CN- (aq) ⇌ |
Ag(CN)2- (aq) |
|
I |
0.03903 |
0.800 |
|
|
C |
-0.03903 |
-20.03903 |
+0.03903 |
|
E |
|
0.72194 |
0.03903 |
Remarque : une petite quantité de Ag(CN)2– réagira pour régénérer Ag+ … les concentrations de CN– et de Ag(CN)2– ne sont pas affectées.
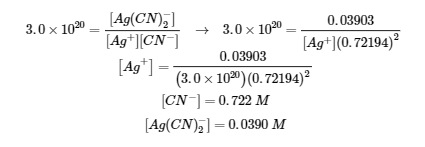
4. (a)
![]()
|
|
A (g) |
2 B (g) |
2 C (g) |
|
I |
0.500 |
0.500 |
0 |
|
C |
-0.245 |
-0.245 |
+0.489 |
|
E |
0.255 |
0.011 |
0.489 |
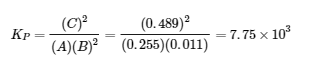
(b)
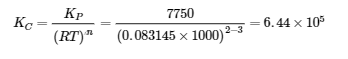
Ptotal = 20.0 bar = PCH4 + PCO2. Since nCH4 = nCO2 (équimolaire), cela signifie que chaque gaz a une pression partielle initiale de 10,0 bar.
|
|
CH4 (g) |
CO2 (g) |
2 CO (g) |
2 H2 (g) |
|
I |
10.0 |
10.0 |
0 |
0 |
|
C |
-x |
-x |
+2x |
+2x |
|
E |
0.246 |
0.2 |
19.6 |
19.6 |
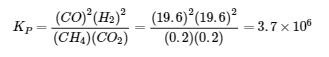
0.83
Divisez la constante d’équilibre de l’équation 1 par 2 et la constante d’équilibre multiple de l’équation 2 par -1 (car vous devez la retourner) ; ajoutez les constantes d’équilibre modifiées pour obtenir 0,83.
Chapitre 5 – Équilibres acide/base
- NH4+ (aq) ⇌ NH3 (aq) + H+ (aq)
E: 0.333 – x 0.333 x x
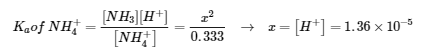
pH = -log(1.36 x 10-5) = 4.87
2. (a)
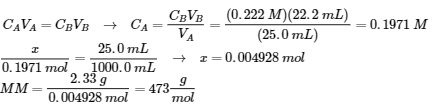
(b) HA (aq) ⇌ H+ (aq) + A– (aq)
E: 0.1971 – x x x
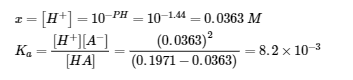
(c) A– (aq) + H2O (l) ⇌ HA (aq) + OH– (aq)
E: 2.000 – x 2.000 x x
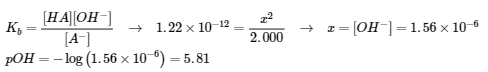
pH = 8.19
3.
|
|
2 A (aq) ⇌ |
B (aq) + |
C (aq) |
|
I |
0.444 |
0.555 |
0.666 |
|
C |
-2x |
+x |
+x |
|
E |
0.444 – 2x |
0.555 + x |
0.666 + x |
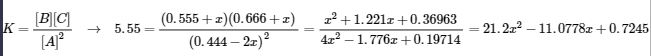
21.2x2 – 11.0778x + 0.7245 = 0 → x = 0.4459 and 0.0765
(Note : utiliser une formule quadratique pour trouver les valeurs de x et x = 0,4459 est impossible, donc nous utilisons 0,0765)
[A] = 0.44 – 2(0.0765) = 0.291 M
(b)
 ∴ pOH = 2.29 and pH = 11.71
∴ pOH = 2.29 and pH = 11.71
4.
pOH = 14 – pH – 3.45
[OH-] = 10-3.45 = 3.55 x 10-4 M
Soit B représente la base, N(CH3)3,
|
|
B |
H2O |
OH- |
HB |
|
I |
[B] |
– |
0 |
0 |
|
C |
-x |
– |
+x |
+x |
|
E |
[B] – x |
– |
x |
X |
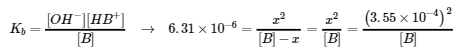
[B] = 0.0200 M
Vérifiez :![]()
5. (a) pH initial
|
|
HA |
H2O |
H3O+ |
A- |
|
I |
0.090 |
– |
0 |
0 |
|
C |
-x |
– |
+x |
+x |
|
E |
0.090 – x |
– |
x |
X |
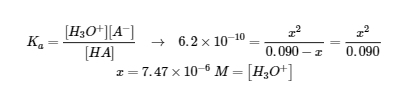
Vérifiez :![]()
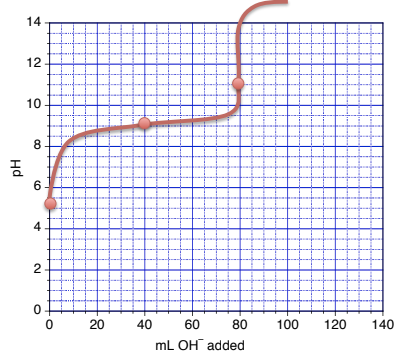
(b) Au demi-point d’équivalence : pH = pKa = –log(6,2 x 10-10) = 9,21 (après ajout de 40 ml)
(c) Au point d’équivalence
mol HA = mol OH– ajouté = 0,0072 mol (ce qui correspond à l’ajout de 80,0 ml de base)
nouveau [A–] = 0,0072 mol/(0,080 L + 0,080 L) = 0,0450 M
L’OCl– est une base conjuguée d’un acide faible, donc il s’hydrolyse :
|
|
A- |
H2O |
HA |
OH- |
|
I |
0.045 |
– |
0 |
0 |
|
C |
-x |
– |
+x |
+x |
|
E |
0.045 – x |
– |
x |
x |
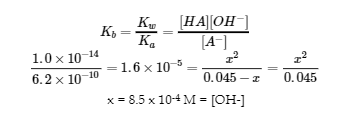
x = 8,5 x 10-4 M = [OH–]
pOH = -log(8,5 x 10-4) = 3,07
pH = 14 – 3,07 = 10,93
Chapitre 6 – Équilibres ioniques dans les systèmes aqueux
La masse molaire de Mg(PO4)2 est de 262,86 g/mol
|
|
Mg(PO4)2(s) ⇌ |
3 Mg+ (aq) + |
2 PO43- (aq) |
|
I |
|
|
|
|
C |
|
+ 3x |
+ 2x |
|
E |
|
3x |
2x |
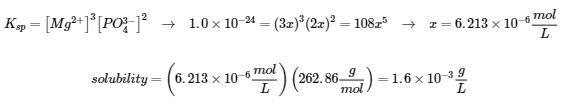
|
|
Mg(PO4)2(s) ⇌ |
3 Mg2+ (aq) + |
2 PO43- (aq) |
|
I |
|
0.30 |
|
|
C |
|
+ 3x |
+ 2x |
|
E |
|
0.30 + 3x 0.30 |
2x |
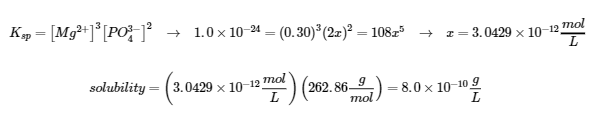
|
|
NH3 (aq) + |
H+ (aq) ⇌
|
NH4+(aq) |
|
I |
0.7103 |
0.1701 |
|
|
C |
– 0.1701 |
– 0.1701 |
+ 0.1701 |
|
E |
0.5402 |
|
0.1701 |
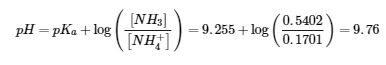
(b) 1,00 g de NaOH (0,0250 mol) consomme 0,0250 mol de NH4+ (aq) et produit 0,0250 mol de NH3 (aq)
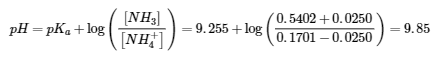
(c) 1,00 g de HCl (0,0274 mol) consomme 0,0274 mol de NH3 (aq) et produit 0,0274 mol de NH4+ (aq)
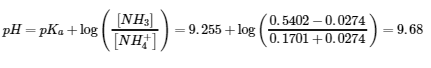
3. Le Ba(OH)2 a 2 groupes de OH-, donc CAVA = 2 CBVB
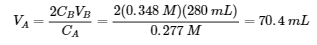
Au point d’équivalence, le volume est de (70,4 ml + 28,0 ml) = 98,4 ml
Tout l’acide acétique est converti en CH3COO–, une base faible :
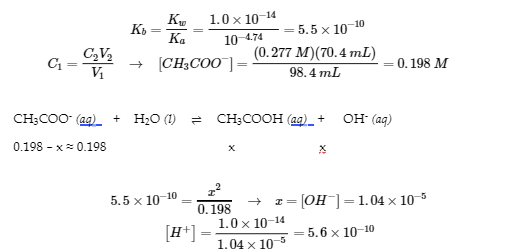
4. pH = 9,02
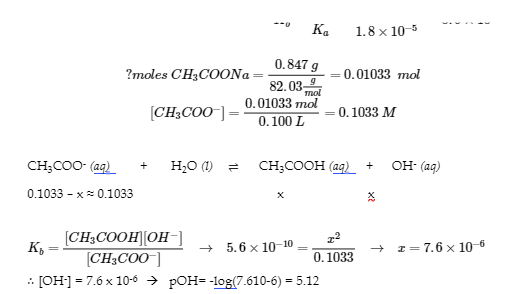
pH = 14 – pOH à pH=8,88
5. (a)
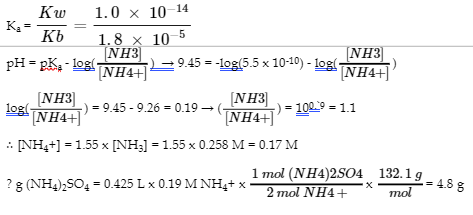
(b)
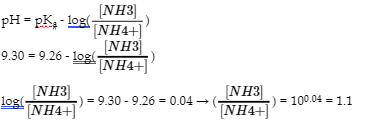
Pour abaisser le pH à 9,30, il faut ajouter de l’acide. Mais en quelle quantité ?
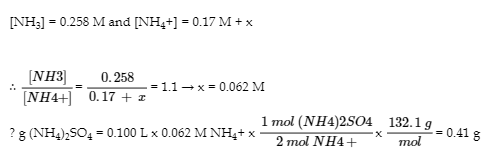
Amount: 0.41 g
6. (a) PbI2
(b)
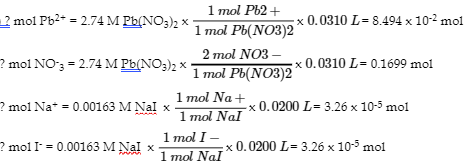
|
|
Pb2+ |
I– |
PbI2(s) |
|
B |
8 494 x 10-2 mol |
|
0 |
|
A |
|
3,26 x 10-5 mol |
|
|
M |
-0,5 x 3,26 x 10-5 mol |
-3,26 x 10-5 mol |
+0,5 x 3,26 x 10-5 mol |
|
A |
8 494 x 10-2 mol |
0 |
1,63 x 10-5 mol |
1,63 x 10-5 mol de précipités de PbI2 et le volume total est de 20,0 ml + 30,0 ml = 51,0 ml
? [Pb2+] = 8.494 x 10-2 mol/0.0510 L = 1.665 M
? [NO–3] = 0.1699 mol/0.0510 L = 3.33 M
? [Na+] = 3.26 x 10-5 mol/0.0510 L = 6.39 x 10-4 M
? [I-] = 0 mol/0.0510 L = 0 M
7. Encerclé → Ca(CN)2 et LiF
Souligné → KCl et CuNO3

