8.3 – Dualité onde-particule de la matière et de l’énergie

Einstein supposait initialement que les photons avaient une masse nulle, ce qui en faisait une sorte de particule particulière. En 1905, cependant, il a publié sa théorie spéciale de la relativité, qui met en relation l’énergie et la masse selon l’équation suivante :

Équation 8.3.1 Relation énergie-masse

Selon cette théorie, un photon de longueur d’onde λ et de fréquence ν a une masse non nulle, qui est donnée comme suit :

Équation 8.3.2 Relation énergie-masse du photon

En d’autres termes, la lumière, qui avait toujours été considérée comme une onde, possède également des propriétés typiques des particules, une condition connue sous le nom de dualité onde-particule (principe selon lequel la matière et l’énergie ont des propriétés typiques à la fois des ondes et des particules). Selon les conditions, la lumière peut être considérée soit comme une onde, soit comme une particule.

L’une des premières personnes à s’intéresser au comportement particulier du monde microscopique fut Louis de Broglie. Il a posé la question suivante : Si le rayonnement électromagnétique peut avoir un caractère particulaire, les électrons et autres particules submicroscopiques peuvent-ils avoir un caractère ondulatoire ? Dans sa thèse de doctorat de 1925, de Broglie a étendu aux particules matérielles la dualité onde-particule de la lumière utilisée par Einstein pour résoudre le paradoxe de l’effet photoélectrique. Il a prédit qu’une particule ayant une masse m et une vitesse v (c’est-à-dire une quantité de mouvement linéaire p) devrait également présenter le comportement d’une onde avec une longueur d’onde de valeur λ, donnée par cette expression dans laquelle h est la constante de Planck bien connue :

Équation 8.3.3 Équation du moment cinétique de la longueur d’onde

C’est ce qu’on appelle la longueur d’onde de de Broglie. Contrairement aux autres valeurs de λ abordées dans ce chapitre, la longueur d’onde de de Broglie est une caractéristique des particules et autres corps, et non du rayonnement électromagnétique (notez que cette équation fait intervenir la vitesse [v, m/s], et non la fréquence [v, Hz]. Bien que ces deux symboles semblent presque identiques, ils signifient des choses très différentes). Alors que Bohr avait postulé que l’électron était une particule orbitant autour du noyau dans des orbites quantifiées, de Broglie a soutenu que l’hypothèse de quantification de Bohr pouvait être expliquée si l’électron n’était pas considéré comme une particule, mais plutôt comme une onde stationnaire circulaire telle que seul un nombre entier de longueurs d’onde pouvait s’insérer exactement dans l’orbite (Figure 8.3.1.).

2πr = nλ, n = 1, 2, 3, …

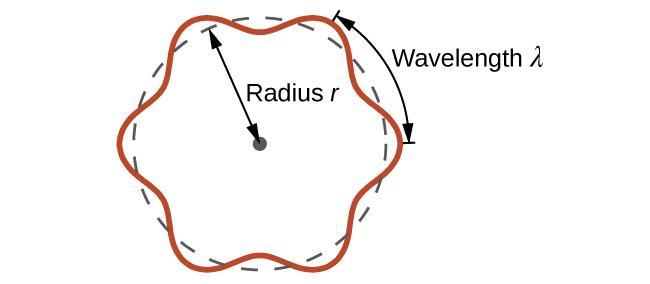
Figure 8.3.1. Si l’on considère l’électron comme une onde qui tourne autour du noyau, un nombre entier de longueurs d’onde doit s’insérer dans l’orbite pour que ce comportement d’onde stationnaire soit possible.

Pour une orbite circulaire de rayon r, la circonférence est de 2πr, et donc la condition de de Broglie est :

Puisque l’expression de de Broglie relie la longueur d’onde à la quantité de mouvement et, par conséquent, à la vitesse, ceci implique :

Cette expression peut être réarrangée pour donner la formule de Bohr pour la quantification de l’élan angulaire :

Équation 8.3.4 Quantification de l’élan angulaire

L’élan angulaire classique L pour un mouvement circulaire est égal au produit du rayon du cercle par l’élan de la particule en mouvement p.

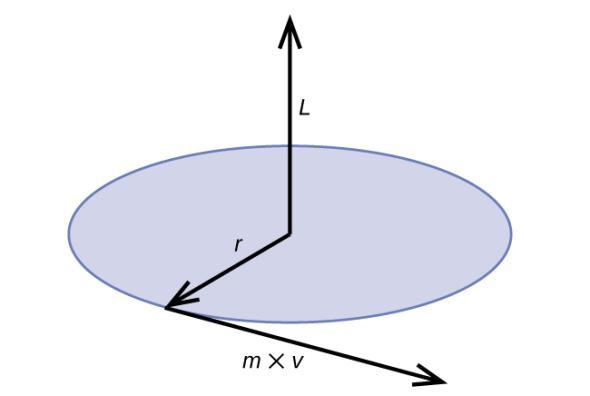
Figure 8.3.2. Le diagramme montre l’élan angulaire pour un mouvement circulaire.

Peu de temps après que de Broglie ait proposé la nature ondulatoire de la matière, deux scientifiques des Laboratoires Bell, C. J. Davisson et L. H. Germer, ont démontré expérimentalement que les électrons peuvent avoir un comportement ondulatoire en montrant un modèle d’interférence pour les électrons se déplaçant à travers un motif atomique régulier dans un cristal. Les couches atomiques régulièrement espacées ont servi de fentes, comme dans d’autres expériences d’interférence. Comme l’espacement entre les couches servant de fentes doit être similaire à la longueur d’onde de l’onde testée pour qu’un modèle d’interférence se forme, Davisson et Germer ont utilisé une cible en nickel cristallin pour leurs “fentes”, car l’espacement des atomes dans le réseau était approximativement le même que les longueurs d’onde de Broglie des électrons qu’ils ont utilisés. La Figure 8.3.3. montre une modèle d’interférence. Elle est étonnamment similaire aux modèles d’interférence de la lumière présentés dans l’exemple de détermination de la fréquence et de la longueur d’onde des rayonnements du sujet 8.1. La Figure 8.3.3. illustre la dualité onde-particule de la matière en observant ce qui se passe lorsque les collisions d’électrons sont enregistrées sur une longue période. Au départ, lorsque seuls quelques électrons ont été enregistrés, ils présentent un comportement clairement particulaire, étant arrivés en petits paquets localisés qui semblent aléatoires. Au fur et à mesure que de plus en plus électrons arrivent et sont enregistrés, un modèle d’interférence clair, qui est la marque d’un comportement ondulatoire, apparaît. Il apparaît donc que, bien que les électrons soient de petites particules localisées, leur mouvement ne suit pas les équations du mouvement impliquées par la mécanique classique, mais qu’il est régi par une sorte d’équation d’onde qui régit une distribution de probabilité, même pour le mouvement d’un seul électron. Ainsi, la dualité onde-particule observée pour la première fois avec les photons est en fait un comportement fondamental intrinsèque à toutes les particules quantiques.

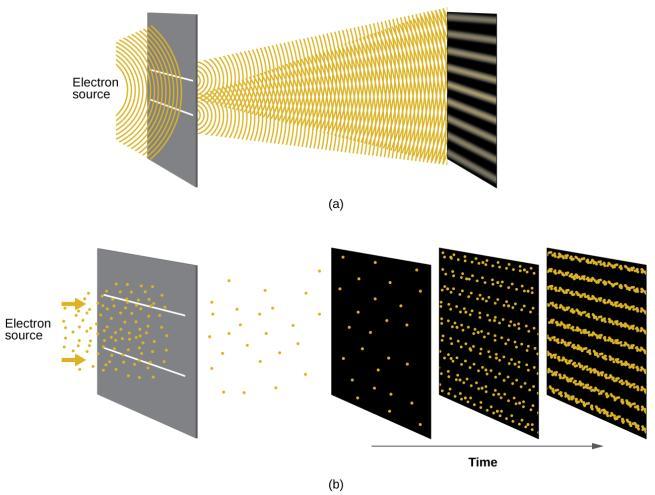
Figure 8.3.3. (a) Le modèle d’interférence des électrons traversant des fentes très rapprochées démontre que les particules quantiques telles que les électrons peuvent présenter un comportement ondulatoire. (b) Les résultats expérimentaux illustrés ici démontrent la dualité onde-particule des électrons. Les électrons passent à travers des fentes très rapprochées, formant un modèle d’interférence, avec un nombre croissant d’électrons enregistrés de l’image de gauche à celle de droite. Avec seulement quelques électrons enregistrés, il est clair que les électrons arrivent sous forme de “particules” individuelles localisées, mais dans une tendance apparemment aléatoire. Au fur et à mesure que les électrons arrivent, un modèle d’interférence semblable à une onde commence à émerger. Notez que la probabilité de la localisation finale de l’électron est toujours régie par la distribution de type ondulatoire, même pour un seul électron, mais elle peut être observée plus facilement si de nombreuses collisions d’électrons ont été enregistrées.

Regardez le dessin animé Dr. Quantum – Expérience de la double fente pour une description facile à comprendre de la dualité onde-particule et des expériences associées.

Exemple 8.3.1 – Calcul de la longueur d’onde d’une particule

Si un électron se déplace à une vitesse de 1,000 × 10⁷ m s^-1 et a une masse de 9,109 × 10^-28 g, quelle est sa longueur d’onde ?

Solution

Nous pouvons utiliser l’équation de de Broglie pour résoudre ce problème, mais nous devons d’abord effectuer une conversion des unités de la constante de Planck. Vous avez appris précédemment que 1 J = 1 kg m²/s². Ainsi, nous pouvons écrire h = 6,626 × 10^-34 J s comme 6,626 × 10^-34 kg m²/s.

C’est une petite valeur, mais elle est nettement plus grande que la taille d’un électron dans la vision classique (d’une particule). Cette taille est du même ordre de grandeur que la taille d’un atome. Cela signifie que le comportement ondulatoire de l’électron sera perceptible dans un atome.

Vérifiez votre apprentissage 8.3.1 – Calcul de la longueur d’onde d’une particule

Calculez la longueur d’onde d’une balle de softball d’une masse de 100 g se déplaçant à une vitesse de 35 m s^-1, en supposant qu’elle peut être modélisée comme une particule unique.

Réponse

1,9 × 10^-34 m. Nous ne pensons jamais qu’une balle de baseball lancée a une longueur d’onde, car cette longueur d’onde est si petite qu’elle est impossible à détecter par nos sens ou tout autre instrument connu (à proprement parler, la longueur d’onde d’une vraie balle de baseball correspondrait aux longueurs d’onde des atomes et molécules qui la composent, qui, bien que beaucoup plus grandes que cette valeur, seraient encore microscopiques). La longueur d’onde de de Broglie n’est appréciable que pour la matière qui a une très petite masse et/ou une très grande vitesse.

Werner Heisenberg a étudié les limites de la précision avec laquelle nous pouvons mesurer les propriétés d’un électron ou d’autres particules microscopiques. Il a déterminé qu’il existe une limite fondamentale à la précision avec laquelle on peut mesurer simultanément la position et la quantité de mouvement d’une particule. Plus nous mesurons avec précision la quantité de mouvement d’une particule, moins nous pouvons déterminer avec précision sa position à ce moment-là, et vice versa. Ceci est résumé dans ce que nous appelons aujourd’hui le principe d'incertitude d'Heisenberg : il est fondamentalement impossible de déterminer simultanément et exactement à la fois la quantité de mouvement et la position d’une particule. Pour une particule de masse m se déplaçant à la vitesse v_x dans la direction x (ou de manière équivalente avec une quantité de mouvement p_x), le produit de l’incertitude sur la position, Δx, et de l’incertitude sur la quantité de mouvement, Δp_x, doit être supérieur ou égal à ℏ / 2 (rappelons que ℏ = h / (2π), la valeur de la constante de Planck divisée par 2π).

Équation 8.3.5 Principe d’incertitude d’Heisenberg

Cette équation nous permet de calculer la limite de la précision avec laquelle nous pouvons connaître à la fois la position simultanée d’un objet et son élan. Par exemple, si nous améliorons notre mesure de la position d’un électron de manière à ce que l’incertitude sur la position (Δx) ait une valeur de, disons, 1 pm (10^-12 m, environ 1% du diamètre d’un atome d’hydrogène), alors notre détermination de sa quantité de mouvement doit avoir une incertitude d’au moins

La valeur de ħ n’est pas grande, donc l’incertitude de la position ou l’élan d’un objet macroscopique comme une balle de baseball est trop insignifiante pour être observée. Cependant, la masse d’un objet microscopique tel qu’un électron est suffisamment petite pour que l’incertitude puisse être grande et significative.

Il convient de noter que le principe d’incertitude d’Heisenberg ne se limite pas aux incertitudes de position et de l’élan, mais qu’il relie également d’autres variables dynamiques. Par exemple, lorsqu’un atome absorbe un photon et effectue une transition d’un état d’énergie à un autre, l’incertitude sur l’énergie et l’incertitude sur le temps nécessaire à la transition sont liées de manière similaire, comme ΔE Δt ≥. ℏ / 2. Comme nous le verrons plus loin, même les composantes vectorielles du moment angulaire ne peuvent pas toutes être spécifiées exactement simultanément.

Le principe d’Heisenberg impose des limites ultimes à ce qui est connaissable en science. On peut montrer que le principe d’incertitude est une conséquence de la dualité onde-particule, qui est au cœur de ce qui distingue la théorie quantique moderne de la mécanique classique. Rappelons que les équations du mouvement obtenues à partir de la mécanique classique sont des trajectoires où, à tout instant donné, la position et la quantité de mouvement d’une particule peuvent être déterminées exactement. Le principe d’incertitude d’Heisenberg implique qu’une telle vision est intenable dans le domaine microscopique et que des limitations fondamentales régissent le mouvement des particules quantiques. Cela ne signifie pas que les particules microscopiques ne se déplacent pas selon des trajectoires, mais simplement que les mesures des trajectoires sont limitées dans leur précision. Dans le domaine de la mécanique quantique, les mesures introduisent des changements dans le système qui est observé.

Lisez cet article qui décrit une récente démonstration macroscopique du principe d’incertitude appliqué à des objets microscopiques.

★ Questions

1. Calculez la longueur d’onde d’une balle de baseball, dont la masse est de 149 g et la vitesse de 100 mi/h.

2. Calculez la longueur d’onde d’un neutron qui se déplace à 3,00 × 10³ m/s (en Å ou pm).

3. Calculez la longueur d’onde (en mètres) associée à une balle de 42 g dont la vitesse est de 80 m/s.

4. Calculez les longueurs d’onde de de Broglie des éléments suivants :

a) Une balle de 8g avec une vitesse de 340ms^-1.

b) Une particule de 10^-5g avec une vitesse de 10^-5ms^-1.

c) Une particule de 10^-8g avec une vitesse de 10^-8ms^-1.

d) Un électron se déplaçant à une vitesse de 4,8 x 10⁶ ms^-1.

Réponses

1. 9,95 x 10^-35

2. 1,32 Å, soit 132 pm

3. 1,97 x 10^-34 m

4. (a) 2,44 x 10^-33 (b) 6,626 x 10^-21 (c) 6,626 x 10^-15 (d) 1,52 x 10^-10