Annexe C | Concepts mathématiques essentiels

Notation scientifique/exponentielle

La notation scientifique (ou exponentielle) est utilisée pour exprimer des nombres très grands et très petits comme produit de deux nombres. Le premier nombre du produit, le terme numérique, est généralement un nombre qui n’est pas inférieur à 1 et pas supérieur à 10. Le deuxième nombre du produit, le terme exponentiel, s’écrit 10 avec un exposant. Voici quelques exemples de notation exponentielle :

1000	=	1 × 103
100	=	1 × 102
10	=	1 × 101
1	=	1 × 100
0,1	=	1 × 10-1
0,001	=	1 × 10-3
2386	=	2,386 × 1000 = 2,386 × 103
0,123	=	1,23 × 0.1 = 1,23 × 10-1

La puissance (exposant) de 10 est égale au nombre de décimales décalées pour donner le nombre de chiffres. La méthode exponentielle est particulièrement utile pour la notation des très grands et très petits nombres. Par exemple, 1 230 000 000 = 1,23 × 10⁹, et 0,00000000036 = 3,6 × 10^-10.

Ajout d’exponentiels

Convertissez tous les nombres à la même puissance de 10, ajoutez les termes numériques des nombres et, le cas échéant, reconvertissez le terme numérique en un nombre compris entre 1 et 10 en ajustant le terme exponentiel.

Ajout d’exponentiels

Exemple C.1

Ajouter 5,00 × 10^-5 et 3,00 × 10^-3.

Solution

3,00×10-3=300×10-5(5,00×10-5)+(300×10-5)=305×10-5=3,05×10-3

Soustraction des exponentielles

Convertissez tous les nombres à la même puissance de 10, prenez la différence des termes numériques et, le cas échéant, reconvertissez le terme numérique en un nombre compris entre 1 et 10 en ajustant le terme exponentiel.

Soustraction des exponentielles

Exemple C.2

Soustrayez 4,0 × 10^-7 de 5,0 × 10^-6.

Solution

Multiplication des exponentiels

Multipliez les termes numériques de la manière habituelle et ajoutez les exposants des termes exponentiels.

Multiplier les exponentielles

Exemple C.3

Multipliez 4,2 × 10^-8 par 2,0 × 10³.

Solution

(4,2×10-8)×(2,0×103)=(4,2×2,0)×10-8++3=8,4×10-5

Division des exposés des motifs

Divisez le terme numérique du numérateur par le terme numérique du dénominateur et soustrayez les exposants des termes exponentiels.

Diviser les exponentiels

Exemple C.4

Divisez 3,6 × 10⁵ par 6,0 × 10^-4.

Solution

3,6×10-56,0×10-4=3,66,0×10(-5)-(-4)=0,60×10-1=6,0×10-2

La quadrature du cercle des exponentiels

Placez le terme numérique au carré de la manière habituelle et multipliez l’exposant du terme exponentiel par 2.

La quadrature du cercle exponentiel

Exemple C.5

Placez le nombre 4,0 × 10^-6 au carré.

Solution

4,0×10-62=4×4×102×-6=16×10-12=1,6×10-11

Cubage des exponentiels

Cubez le terme numérique de la manière habituelle et multipliez l’exposant du terme exponentiel par 3.

Cubage des exponentiels

Exemple C.6

Cube le nombre 2 × 10⁴.

Solution

2×1043=2×2×2×103×4=8×1012

Prendre racine dans l’exponentiel

Si nécessaire, diminuez ou augmentez le terme exponentiel de manière à ce que la puissance de 10 soit divisible par 2. Extrayez la racine carrée du terme numérique et divisez le terme exponentiel par 2.

Trouver la racine carrée des exponentielles

Exemple C.7

Trouvez la racine carrée de 1,6 × 10^-7.

Solution

1,6×10-7=16×10-816×10-8=16×10-8=16×10-82=4,0×10-4

Chiffres significatifs

Un apiculteur signale qu’il possède 525 341 abeilles. Les trois derniers chiffres du nombre sont évidemment inexacts, car pendant que l’apiculteur comptait les abeilles, certaines sont mortes et d’autres ont éclos, ce qui rend assez difficile la détermination du nombre exact d’abeilles. Il aurait été plus raisonnable que l’apiculteur déclare le nombre 525 000. En d’autres termes, les trois derniers chiffres ne sont pas significatifs, sauf pour fixer la position du point décimal. Leurs valeurs exactes n’ont aucune signification utile dans cette situation. Lorsque vous déclarez des quantités, n’utilisez qu’autant de chiffres significatifs que l’exactitude de la mesure le justifie.

L’importance des chiffres significatifs réside dans leur application au calcul fondamental. En addition et en soustraction, la somme ou la différence doit contenir autant de chiffres à droite de la décimale que dans le moins certain des nombres utilisés dans le calcul (indiqué par un soulignement dans l’exemple suivant).

Addition et soustraction avec des chiffres significatifs

Exemple C.8

Ajouter 4,383 g et 0,0023 g.

Solution

4,383 g

0,0023 g

4,385 g

Dans la multiplication et la division, le produit ou le quotient ne doit pas contenir plus de chiffres que celui du facteur contenant le moins de chiffres significatifs.

Multiplication et division avec des chiffres significatifs

Exemple C.9

Multipliez 0,6238 par 6,6.

Solution

0,6238 × 6,6 = 4,1

Lorsque nous prenons le log d’un nombre, nous exprimons ce nombre en notation scientifique (

) et calculer le logarithme pour les deux termes a et 10^b séparément (sur la base de la règle du logarithme d’un produit de deux nombres). La valeur obtenue à partir du logarithme (a) sera exprimée par le même nombre de chiffres significatifs, qui sera ensuite ajouté à la valeur du logarithme (10^b).

Opérations logarithmiques avec chiffres significatifs

Exemple C.10

Prenez le logarithme de 22,38 en base 10.

Solution

log22,38=log2,238×101=log2¯,238¯log101=0,3498¯60…+1,00000…=1,3499¯

Lorsque vous arrondissez des chiffres, augmentez le chiffre retenu de 1 s’il est suivi d’un chiffre supérieur à 5 (“arrondir à l’entier supérieur”). Ne changez pas le chiffre retenu si les chiffres qui suivent sont inférieurs à 5 (“arrondir à l’inférieur”). Si le chiffre retenu est suivi de 5, arrondissez au chiffre supérieur si le chiffre retenu est impair, ou arrondissez au chiffre inférieur s’il est pair (après arrondi, le chiffre retenu sera donc toujours pair).

REMARQUE : Les éléments brièvement abordés ici concernant les chiffres significatifs sont abordés de manière beaucoup plus détaillée dans la section “Chiffres significatifs et incertitude” du chapitre d’introduction – voir cette section pour des explications plus détaillées, des exemples et des exercices pratiques concernant l’utilisation des chiffres significatifs.

L’utilisation des logarithmes et des nombres exponentiels

Le logarithme commun d’un nombre (log) est la puissance à laquelle 10 doit être porté pour être égal à ce nombre. Par exemple, le logarithme commun de 100 est 2, car 10 doit être porté à la deuxième puissance pour être égal à 100. D’autres exemples suivent.

Logarithmes et nombres exponentiels
Numéro	Nombre exprimé de manière exponentielle	Logarithme commun
1000	103	3
10	101	1
1	100	0
0,1	10-1	-1
0,01	10-3	-3

Tableau C.1 Logarithmes et nombres exponentiels

Quel est le logarithme commun de 60 ? Puisque 60 se situe entre 10 et 100, qui ont des logarithmes de 1 et 2, respectivement, le logarithme de 60 est 1,7782, c’est-à-dire,

60 = 10^1.7782

Le logarithme commun d’un nombre inférieur à 1 a une valeur négative. Le logarithme de 0,03918 est de -1,4069, ou

0,03918=10-1,4069=1101,4069

Pour obtenir le logarithme commun d’un nombre, utilisez le bouton “log” de votre calculatrice. Pour calculer un nombre à partir de son logarithme, prenez le logarithme inverse du logarithme, ou calculez 10^x (où x est le logarithme du nombre).

Le logarithme naturel d’un nombre (ln) est la puissance à laquelle e doit être porté pour être égal au nombre ; e est la constante 2,7182818. Par exemple, le logarithme naturel de 10 est 2,303 ; c’est-à-dire,

10 = e^2,303 = 2,7182818^2,303

Pour obtenir le logarithme naturel d’un nombre, utilisez le bouton ln de votre calculatrice. Pour calculer un nombre à partir de son logarithme naturel, entrez le logarithme naturel et prenez l’inverse ln du logarithme naturel, ou calculez e^x (où x est le logarithme naturel du nombre).

Les logarithmes sont des exposants ; ainsi, les opérations impliquant des logarithmes suivent les mêmes règles que les opérations impliquant des exposants.

Le logarithme d’un produit de deux nombres est la somme des logarithmes des deux nombres.

log xy = log x + log y, et ln xy = ln x + ln y

Le logarithme du nombre résultant de la division de deux nombres est la différence entre les logarithmes des deux nombres.

et

Le logarithme d’un nombre élevé en exposant est le produit de l’exposant et du logarithme du nombre.

log xⁿ = n log x et ln xⁿ = n ln x

La solution des équations quadratiques

Une forme de fonctions mathématiques que vous connaissez probablement très bien sont les fonctions linéaires (ou polynômes du premier ordre) – celles qui sont décrites par l’équation bien connue y = mx + b, où m définit la pente de la droite et b est la valeur qui dicte l’ordonnée à l’origine de la droite sur le graphique. En d’autres termes, le calcul de plusieurs paires x,y à partir d’une seule fonction, leur représentation graphique et la connexion de tous les points entre eux donnent une ligne droite sur le plan cartésien. Tout autre point de données que vous produisez à partir de la fonction se trouvera toujours sur la ligne tracée.

Une autre forme de fonctions mathématiques courantes sont les polynômes du second ordre ou, plus communément, les fonctions quadratiques.

ax² + bx + c = 0

La solution ou les racines de toute équation quadratique peuvent être calculées à l’aide de la formule suivante :

x=-b±b2-4ac2a

C’est ce qu’on appelle communément la formule quadratique. La dérivation pour résoudre x peut être effectuée de différentes manières, dont l’une est illustrée ci-dessous :

ax2+bx+c=04a2x2+4abx+4ac=04a2x2+4abx=-4ac4a2x2+4abx+b2=b2-4ac2ax+b2=b2-4ac2ax+b=±b2-4ac2ax=-b±b2-4acx=-b±b2-4ac2a

Résoudre des équations quadratiques

Exemple C.11

Résoudre l’équation quadratique 3x² + 13x – 10 = 0

Solution

En substituant les valeurs a = 3, b = 13, c = -10 dans la formule, on obtient

x=-13±132-4×3×(-10)2×3

x=-13±169+1206=-13±2896=-13±176

Les deux racines sont donc

et

Graphiques en deux dimensions (x – y)

La relation entre deux propriétés quelconques d’un système peut être représentée graphiquement par un tracé de données bidimensionnel. Un tel graphique a deux axes : un axe horizontal correspondant à la variable indépendante, ou à la variable dont la valeur est contrôlée (x), et un axe vertical correspondant à la variable dépendante, ou à la variable dont la valeur est observée ou mesurée (y).

Lorsque la valeur de y change en fonction de x (c’est-à-dire que différentes valeurs de x correspondent à différentes valeurs de y), on peut tracer ou esquisser un graphique de ce changement. Le graphique peut être produit en utilisant des valeurs spécifiques pour les paires de données (x,y).

Graphique de la dépendance de y par rapport à x

Exemple C.12

x	y
1	5
2	10
3	7
4	14

Ce tableau contient les points suivants : (1,5), (2,10), (3,7) et (4,14). Chacun de ces points peut être tracé sur un graphique et relié pour produire une représentation graphique de la dépendance de y par rapport à x.

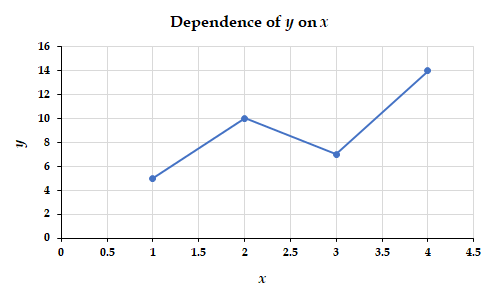
Si la fonction qui décrit la dépendance de y par rapport à x est connue, elle peut être utilisée pour calculer les paires de données x,y qui peuvent ensuite être tracées.

Tracer des paires de données

Exemple C.13

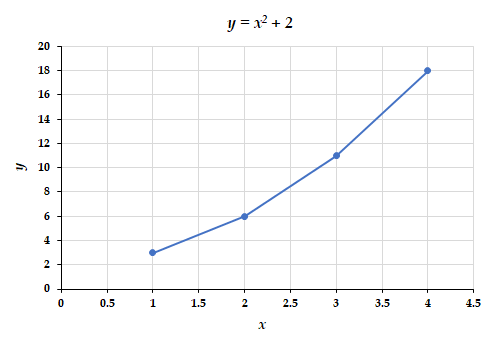
Si nous savons que y = x² + 2, nous pouvons produire un tableau de quelques valeurs (x,y) et ensuite tracer la ligne sur la base des données indiquées ici.

x	y = x2 + 2
1	3
2	6
3	11
4	18