8.4 – Mécanique Quantique

Peu après que de Broglie eut publié ses idées selon lesquelles l’électron d’un atome d’hydrogène pouvait être considéré comme une onde circulaire stationnaire plutôt que comme une particule se déplaçant sur des orbites circulaires quantifiées, comme l’avait soutenu Bohr, Erwin Schrödinger a étendu les travaux de de Broglie en incorporant la relation de Broglie dans une équation d’onde, obtenant ce qui est aujourd’hui connu sous le nom d’équation de Schrödinger. Lorsque Schrödinger a appliqué son équation à des atomes de type hydrogène, il a pu reproduire l’expression de Bohr pour l’énergie et, par conséquent, la formule de Rydberg régissant les spectres de l’hydrogène, et ce sans avoir à invoquer les hypothèses de Bohr sur les états stationnaires et les orbites, les moments angulaires et les énergies quantifiés ; la quantification dans la théorie de Schrödinger était une conséquence naturelle des mathématiques sous-jacentes de l’équation d’onde. Comme de Broglie, Schrödinger considérait initialement l’électron dans l’hydrogène comme une onde physique plutôt que comme une particule, mais alors que de Broglie pensait à l’électron en termes d’ondes stationnaires circulaires, Schrödinger pensait plutôt en termes d’ondes stationnaires tridimensionnelles, ou de fonctions d'onde, représentées par la lettre grecque psi, ѱ. Quelques années plus tard, Max Born a proposé une interprétation de la fonction d’onde ѱ qui est toujours acceptée aujourd’hui : Les électrons sont toujours des particules, et donc les ondes représentées par ѱ ne sont pas des ondes physiques mais, au contraire, des amplitudes de probabilité complexes. Le carré de l’amplitude d’une fonction d’onde ∣ѱ∣² décrit la probabilité que la particule quantique soit présente près d’un certain endroit dans l’espace. Cela signifie que les fonctions d’onde peuvent être utilisées pour déterminer la distribution de la densité de l’électron par rapport au noyau dans un atome. Sous sa forme la plus générale, l’équation de Schrödinger peut s’écrire comme suit :

Équation 8.4.1 Équation de Schrödinger

Les travaux de Schrödinger, ainsi que ceux de Heisenberg et de nombreux autres scientifiques qui ont suivi leurs traces, sont généralement désignés sous le nom de mécanique quantique.

Vous avez peut-être aussi entendu parler de Schrödinger en raison de sa célèbre expérience de pensée. Cette histoire explique les concepts de superposition et d’intrication en relation avec un chat dans une boîte avec du poison.

Comprendre la théorie quantique des électrons dans les atomes

L’objectif de cette section est de comprendre les orbitales électroniques (emplacement des électrons dans les atomes), leurs différentes énergies et d’autres propriétés. L’utilisation de la théorie quantique permet la meilleure compréhension de ces sujets. Cette connaissance est un précurseur des liaisons chimiques.

Comme nous l’avons décrit précédemment, les électrons dans les atomes ne peuvent exister que sur des niveaux d’énergie discrets, mais pas entre eux. On dit que l’énergie d’un électron dans un atome est quantifiée, c’est-à-dire qu’elle ne peut être égale qu’à certaines valeurs spécifiques et qu’elle peut sauter d’un niveau d’énergie à un autre mais pas faire une transition douce ou rester entre ces niveaux.

Les niveaux d’énergie sont marqués d’une valeur n, où n = 1, 2, 3, …. De manière générale, l’énergie d’un électron dans un atome est plus grande pour les grandes valeurs de n. Ce nombre, n, est appelé nombre quantique principal. Le nombre quantique principal définit l’emplacement du niveau d’énergie. Il s’agit essentiellement du même concept que le n de la description de l’atome de Bohr. Un autre nom pour le nombre quantique principal est le nombre de couches. Les couches d’un atome peuvent être considérées comme des sphères concentriques rayonnant à partir du noyau. Les électrons qui appartiennent à une couche spécifique sont plus susceptibles de se trouver dans la zone circulaire correspondante. Plus on s’éloigne du noyau, plus le nombre de couches est élevé, et donc plus le niveau d’énergie est élevé (Figure 8.4.1.). Les protons chargés positivement dans le noyau stabilisent les orbitales électroniques par attraction électrostatique entre les charges positives des protons et les charges négatives des électrons. Ainsi, plus l’électron est éloigné du noyau, plus son énergie est grande.

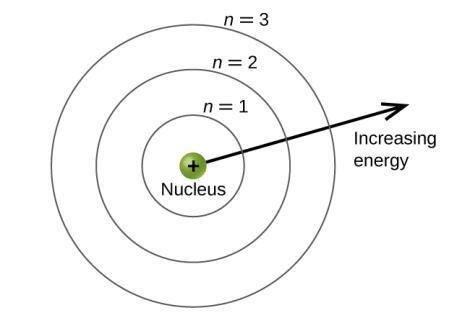
Figure 8.4.1. Les différentes couches sont numérotées par des nombres quantiques principaux.

Ce modèle mécanique quantique de l’emplacement des électrons dans un atome peut être utilisé pour étudier les transitions électroniques, c’est-à-dire les événements au cours desquels un électron passe d’un niveau d’énergie à un autre. Si la transition se fait vers un niveau d’énergie supérieur, de l’énergie est absorbée et le changement d’énergie a une valeur positive. Pour obtenir la quantité d’énergie nécessaire à la transition vers un niveau d’énergie supérieur, un photon est absorbé par l’atome. La transition vers un niveau d’énergie inférieur implique une libération d’énergie, et le changement d’énergie est négatif. Ce processus s’accompagne de l’émission d’un photon par l’atome. L’équation suivante résume ces relations et se base sur l’atome d’hydrogène :

Les valeurs n_f et n_i sont les états d’énergie final et initial de l’électron. L’exemple de calcul de l’énergie et de la longueur d’onde des transitions des électrons dans un système à un électron (Bohr) dans le concept 8.2 du chapitre montre le calcul de ces changements d’énergie.

Le nombre quantique principal est l’un des trois nombres quantiques utilisés pour caractériser une orbitale. Une orbitale atomique, qui est distincte d’une orbite, est une région générale d’un atome dans laquelle il est le plus probable qu’un électron réside. Le modèle mécanique quantique spécifie la probabilité de trouver un électron dans l’espace tridimensionnel autour du noyau et se base sur les solutions de l’équation de Schrödinger. En outre, le nombre quantique principal définit l’énergie d’un électron dans un atome d’hydrogène ou de type hydrogène ou un ion (un atome ou un ion ne comportant qu’un seul électron) et la région générale dans laquelle se trouvent les niveaux d’énergie discrets des électrons dans les atomes et les ions à plusieurs électrons.

Un autre nombre quantique est ℓ (lettre minuscule L), le nombre quantique du moment angulaire. Il s’agit d’un nombre entier qui définit la forme de l’orbitale et qui prend les valeurs suivantes : l = 0, 1, 2, …, n – 1. Cela signifie qu’une orbitale avec n = 1 ne peut avoir qu’une seule valeur de l, l = 0, alors que n = 2 permet l = 0 et l = 1, et ainsi de suite. Le nombre quantique principal définit la taille générale et l’énergie de l’orbitale. La valeur de l spécifie la forme de l’orbitale. Les orbitales ayant la même valeur de l forment une sous-couche. En outre, plus le nombre quantique du moment angulaire est grand, plus le moment angulaire d’un électron sur cette orbitale est grand.

Les orbitales avec l = 0 sont appelées orbitales s (ou sous-couche s). La valeur l = 1 correspond aux orbitales p. Pour un n donné, p orbitales constituent une sous-couche p (par exemple, 3p si n = 3). Les orbitales avec l = 2 sont appelées orbitales d, suivies des orbitales f-, g-, et h pour l = 3, 4, 5, et il existe des valeurs supérieures que nous ne considérerons pas.

Il existe certaines distances du noyau auxquelles la densité de probabilité de trouver un électron situé sur une orbitale particulière est nulle. En d’autres termes, la valeur de la fonction d’onde ψ est nulle à cette distance pour cette orbitale. Une telle valeur de rayon r est appelée un nœud radial. Le nombre de nœuds radiaux dans une orbitale est n – l – 1.

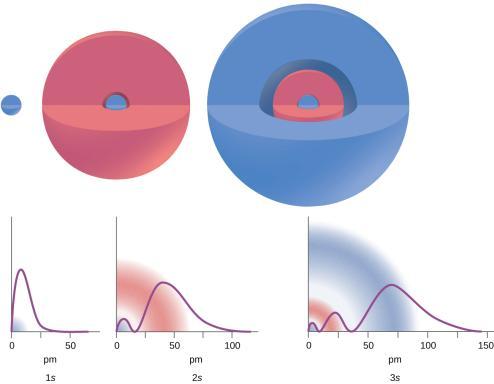
Figure 8.4.2. Les graphiques montrent la probabilité (axe des y) de trouver un électron pour les orbitales 1s, 2s, 3s en fonction de la distance au noyau.

Considérez les exemples de la Figure 8.4.2. Les orbitales représentées sont de type s, donc l = 0 pour toutes. Les graphiques des densités de probabilité montrent qu’il existe 1 – 0 – 1 = 0 endroits où la densité est nulle (nœuds) pour 1s (n = 1), 2 – 0 – 1 = 1 nœud pour 2s et 3 – 0 – 1 = 2 nœuds pour les orbitales 3s.

La distribution de la densité électronique de la sous-couche s est sphérique et la sous-couche p a une forme d’haltère. Les orbitales d et f sont plus complexes. Ces formes représentent les régions tridimensionnelles dans lesquelles l’électron est susceptible de se trouver.

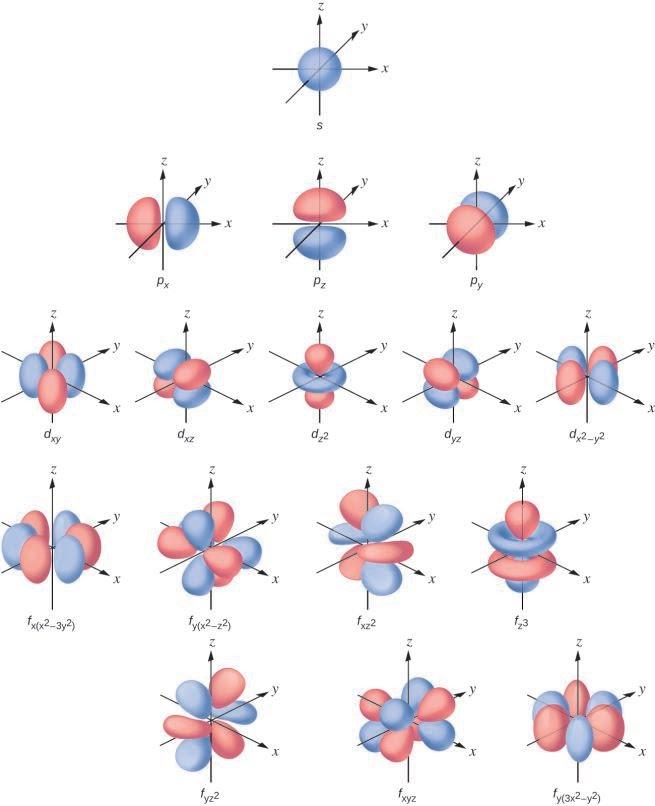
Figure 8.4.3. Formes des orbitales s, p, d et f.

Si un électron a un moment cinétique (l ≠ 0), alors ce vecteur peut pointer dans différentes directions. En outre, la composante z du moment cinétique peut avoir plus d’une valeur. Cela signifie que si un champ magnétique est appliqué dans la direction z, les orbitales avec différentes valeurs de la composante z du moment cinétique auront des énergies différentes résultant de l’interaction avec le champ. Le nombre quantique magnétique, appelé m_ℓ, spécifie la composante z du moment cinétique pour une orbitale particulière. Par exemple, pour une orbitale s, l = 0, et la seule valeur de m_l est zéro. Pour les orbitales p, l = 1, et m_l peut être égal à -1, 0 ou +1. En général, m_l peut être égal à -l, -(l – 1), …, -1, 0, +1, …, (l – 1), l. Le nombre total d’orbitales possibles avec la même valeur de l (une sous-couche) est de 2l + 1. Ainsi, il existe une orbitale s pour l = 0, trois orbitales p pour l = 1, cinq orbitales d pour l = 2, sept orbitales f pour l = 3, et ainsi de suite. Le nombre quantique principal définit la valeur générale de l’énergie électronique. Le nombre quantique du moment angulaire détermine la forme de l’orbitale. Et le nombre quantique magnétique spécifie l’orientation de l’orbitale dans l’espace, comme on peut le voir sur la Figure 8.4.3.

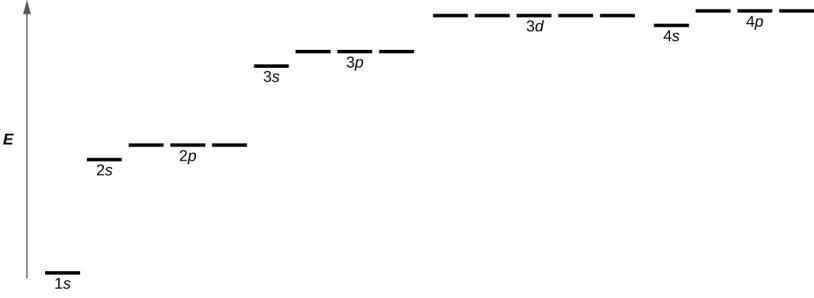
Figure 8.4.4. Le graphique montre les énergies des orbitales électroniques dans un atome à plusieurs électrons.

La Figure 8.4.4. illustre les niveaux d’énergie de diverses orbitales. Le nombre précédant le nom de l’orbitale (comme 2s, 3p, et ainsi de suite) représente le nombre quantique principal, n. La lettre dans le nom de l’orbitale définit la sous-couche avec un nombre quantique de moment angulaire spécifique l = 0 pour les orbitales s, 1 pour les orbitales p, 2 pour les orbitales d. Enfin, il existe plus d’une orbitale possible pour l ≥ 1, chacune correspondant à une valeur spécifique de m_l. Dans le cas d’un atome d’hydrogène ou d’un ion à un électron (comme He⁺, Li²⁺, et ainsi de suite), les énergies de toutes les orbitales avec le même n sont les mêmes. C’est ce qu’on appelle une dégénérescence, et les niveaux d’énergie pour le même nombre quantique principal, n, sont appelés orbitales dégénérées. Cependant, dans les atomes comportant plus d’un électron, cette dégénérescence est éliminée par les interactions électron-électron, et les orbitales qui appartiennent à des sous-couches différentes ont des énergies différentes, comme le montre la Figure 8.4.4. Les orbitales appartenant à la même sous-couche (par exemple ns, np, nd, nf, comme 2p, 3s) sont toujours dégénérées et ont la même énergie.

Si les trois nombres quantiques évoqués dans les paragraphes précédents fonctionnent bien pour décrire les orbitales électroniques, certaines expériences ont montré qu’ils ne suffisaient pas à expliquer tous les résultats observés. Il a été démontré dans les années 1920 que lorsque les spectres de raies de l’hydrogène sont examinés à une résolution extrêmement élevée, certaines raies ne sont pas des pics uniques mais plutôt des paires de raies très rapprochées. C’est ce que l’on appelle la structure fine du spectre, et elle implique qu’il existe de petites différences supplémentaires dans les énergies des électrons, même lorsqu’ils sont situés sur la même orbite. Ces observations ont conduit Samuel Goudsmit et George Uhlenbeck à proposer que les électrons possèdent un quatrième nombre quantique. Ils l’ont appelé le nombre quantique de spin, ou m_s.

Les trois autres nombres quantiques, n, l et m_l, sont des propriétés d’orbitales atomiques spécifiques qui définissent également dans quelle partie de l’espace un électron est le plus susceptible de se trouver. Les orbitales sont le résultat de la résolution de l’équation de Schrödinger pour les électrons dans les atomes. Le spin de l’électron est un autre type de propriété. Il s’agit d’un phénomène quantique complètement différent qui n’a aucun analogue dans le domaine classique. En outre, il ne peut être dérivé de la résolution de l’équation de Schrödinger et n’est pas lié aux coordonnées spatiales normales (telles que les coordonnées cartésiennes x, y et z). Le spin des électrons décrit une “rotation” ou un “tournoiement” intrinsèque des électrons. Chaque électron agit comme une minuscule aimante ou un minuscule objet en rotation avec un moment angulaire, ou comme une boucle avec un courant électrique, même si cette rotation ou ce courant ne peuvent être observés en termes de coordonnées spatiales.

La magnitude du spin global de l’électron ne peut avoir qu’une seule valeur, et un électron ne peut “tourner” que dans l’un des deux états quantifiés. Pensez à une planète par exemple, quelle que soit la position ou la direction de l’axe planétaire, elle ne peut tourner que dans deux directions : “sens horaire” ou “sens antihoraire”. L’un des deux états quantifiés est appelé l’état α, la composante z du spin étant dans la direction positive de l’axe z. Cela correspond au nombre quantique de spin m_s = 12. L’autre est appelé l’état β, la composante z du spin étant négative et m_s = -12. Tout électron, quelle que soit l’orbitale atomique dans laquelle il se trouve, ne peut avoir qu’une seule de ces deux valeurs du nombre quantique de spin. Les énergies des électrons ayant m_s = -12 et m_s = 12 sont différentes si un champ magnétique externe est appliqué.

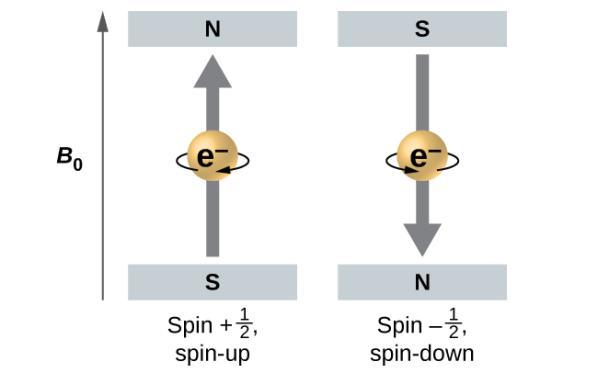
Figure 8.4.5. Électrons avec des valeurs de spin ±12 dans un champ magnétique externe.

La Figure 8.4.5. illustre ce phénomène. Un électron agit comme un petit aimant. Son moment est dirigé vers le haut (dans le sens positif de l’axe z) pour le nombre quantique de spin de 12 et vers le bas (dans la direction négative de l’axe z) pour le nombre quantique de spin de -12 (Remarque : les directions vers le haut et vers le bas sont totalement arbitraires, et résultent d’un accord unanime pour les désigner comme telles). Un aimant a une énergie plus faible si son moment magnétique est aligné avec le champ magnétique externe (l’électron de gauche sur la Figure 8.4.5.) et une énergie plus élevée si le moment magnétique est opposé au champ appliqué. C’est pourquoi un électron avec m_s= 12 a une énergie légèrement inférieure dans un champ externe dans la direction z positive, et un électron avec m_s = -12 a une énergie légèrement supérieure dans le même champ. Ceci est vrai même pour un électron occupant la même orbitale dans un atome. Une raie spectrale correspondant à une transition pour des électrons de la même orbitale mais avec des nombres quantiques de spin différents a deux valeurs possibles d’énergie ; ainsi, la raie dans le spectre montrera une division de structure fine.

★ Questions

1. En quoi le modèle de Bohr et le modèle de mécanique quantique de l’atome d’hydrogène sont-ils similaires ? En quoi sont-ils différents ?

2. Quelles sont les valeurs autorisées pour chacun des quatre nombres quantiques : n, l, m_l et m_s ?

3. Décrivez les propriétés d’un électron associé à chacun des quatre nombres quantiques suivants : n, l, m_l et m_s.

4. Répondez aux questions suivantes :

a) Sans utiliser de nombres quantiques, décrivez les différences entre les couches, les sous-couches et les orbitales d’un atome.

b) Comment les nombres quantiques des couches, sous-couches et orbitales d’un atome diffèrent-ils ?

5. Identifiez la sous-couche dans laquelle se trouvent les électrons ayant les nombres quantiques suivants :

a) n = 2, l = 1

b) n = 4, l = 2

c) n = 6, l = 0

6. Lesquelles des sous-couches décrites dans la question précédente contiennent des orbitales dégénérées ? Combien d’orbitales dégénérées y a-t-il dans chacune ?

7. Identifiez la sous-couche dans laquelle se trouvent les électrons ayant les nombres quantiques suivants :

a) n = 3, l = 2

b) n = 1, l = 0

c) n = 4, l = 3

8. Lesquelles des sous-couches décrites dans la question précédente contiennent des orbitales dégénérées ? Combien d’orbitales dégénérées y a-t-il dans chacune ?

Réponses

1. Les deux modèles comportent un noyau central chargé positivement et des électrons qui se déplacent autour du noyau en fonction du potentiel électrostatique de Coulomb. Le modèle de Bohr suppose que les électrons se déplacent sur des orbites circulaires dont les énergies, le moment angulaire et les rayons sont quantifiés et spécifiés par un seul nombre quantique, n = 1, 2, 3, …, mais cette quantification est une hypothèse ad hoc faite par Bohr pour incorporer la quantification dans une description de l’atome essentiellement basée sur la mécanique classique. Bohr a également supposé que les électrons en orbite autour du noyau n’émettent ou n’absorbent normalement pas de rayonnement électromagnétique, mais qu’ils le font lorsque l’électron change d’orbite. Dans le modèle de la mécanique quantique, les électrons ne se déplacent pas sur des orbites précises (de telles orbites violent le principe d’incertitude d’Heisenberg) et, à la place, une interprétation probabiliste de la position de l’électron à tout instant est utilisée, avec une fonction mathématique ψ appelée fonction d’onde qui peut être utilisée pour déterminer la distribution de probabilité spatiale de l’électron. Ces fonctions d’onde, ou orbitales, sont des ondes stationnaires tridimensionnelles qui peuvent être spécifiées par trois nombres quantiques qui découlent naturellement de leurs mathématiques sous-jacentes (aucune hypothèse ad hoc n’est requise) : le nombre quantique principal, n (le même que celui utilisé par Bohr), qui spécifie des couches telles que les orbitales ayant le même n ont toutes la même énergie et approximativement la même étendue spatiale ; le nombre quantique de moment angulaire l, qui est une mesure du moment angulaire de l’orbitale et correspond aux formes générales des orbitales, tout en spécifiant des sous-couches telles que les orbitales ayant le même l (et n) ont toutes la même énergie ; et le nombre quantique d’orientation m, qui est une mesure de la composante z du moment angulaire et correspond aux orientations des orbitales. Le modèle de Bohr donne la même expression pour l’énergie que l’expression de la mécanique quantique et, par conséquent, les deux expliquent correctement le spectre discret de l’hydrogène (un exemple d’une bonne réponse pour de mauvaises raisons, un phénomène avec lequel de nombreux étudiants en chimie peuvent sympathiser), mais donne une expression erronée pour le moment angulaire (les orbites de Bohr ont nécessairement toutes un moment angulaire non nul, mais certaines orbitales quantiques [orbitales s] peuvent avoir un moment angulaire nul).

2. n = 1,2,3,4…

l = 0 à (n-1)

m_l = -1 à +1

m_s = -½ à +½

3. n détermine la plage générale pour la valeur de l’énergie et les distances probables que l’électron peut avoir par rapport au noyau. l détermine la forme de l’orbitale. m_l détermine l’orientation des orbitales de même valeur l les unes par rapport aux autres. m_s détermine le spin d’un électron.

4.

(a)

couche: ensemble d’orbitales dans le même niveau d’énergie.

sous-couche: ensemble d’orbitales ayant le même niveau d’énergie et forme (s, p, d, ou f)

orbitale: peut contenir jusqu’à 2 électrons

(b)

couche: ensemble d’orbitales dans le même niveau d’énergie.

sous-couche: ensemble d’orbitales ayant le même niveau d’énergie et forme (s, p, d, ou f)

orbitale: peut contenir jusqu’à 2 électrons

5. (a) 2p; (b) 4d; (c) 6s

6. (a) 3 orbitales; (b) 5 orbitales; (c) 1 orbitale

7. (a) 3d; (b) 1s; (c) 4f

8. (a) 5 orbitales; (b) 1 orbitale; (c) 7 orbitales