8.2 – Atomic Spectra

Un autre paradoxe de la théorie électromagnétique classique auquel les scientifiques de la fin du XIXe siècle ont été confrontés concerne la lumière émise par les atomes et les molécules. Lorsque des solides, des liquides ou des gaz condensés sont suffisamment chauffés, ils émettent une partie de l’énergie excédentaire sous forme de lumière. Les photons produits de cette manière ont une gamme d’énergies, et produisent ainsi un spectre continu dans lequel une série ininterrompue de longueurs d’onde est présente. La plupart de la lumière produite par les étoiles (y compris notre soleil) est produite de cette manière. Vous pouvez voir toutes les longueurs d’onde visibles de la lumière solaire en utilisant un prisme pour les séparer. Comme le montre la Figure 8.1.8 du concept précédent, la lumière du soleil contient également de la lumière UV (longueurs d’onde plus courtes) et de la lumière IR (longueurs d’onde plus longues) qui peuvent être détectées à l’aide d’instruments, mais qui sont invisibles à l’œil humain. Les solides incandescents (qui brillent), tels que les filaments de tungstène des lampes à incandescence, émettent également une lumière qui contient toutes les longueurs d’onde de la lumière visible. Ces spectres continus peuvent souvent être approximés par les courbes de rayonnement du corps noir à une température appropriée, comme celles illustrées à la Figure 8.1.9 de la section précédente.

Contrairement aux spectres continus, la lumière peut également se présenter sous la forme de spectres discrets ou de spectres de raies ayant des largeurs de raies très étroites réparties dans les régions spectrales, comme celles illustrées à la Figure 8.2.2. L’excitation d’un gaz à faible pression partielle à l’aide d’un courant électrique, ou son chauffage, produira des spectres de raies. Les ampoules fluorescentes et les panneaux au néon fonctionnent de cette manière (Figure 8.2.1.). Chaque élément présente son propre ensemble caractéristique de lignes, tout comme les molécules, bien que leurs spectres soient généralement beaucoup plus complexes.

Figure 8.2.1. Les panneaux au néon fonctionnent en excitant un gaz à faible pression partielle à l’aide d’un courant électrique. Ce panneau montre les effets artistiques élaborés qui peuvent être obtenus. (Crédit : Dave Shaver)

Chaque ligne d’émission est constituée d’une seule longueur d’onde de lumière, ce qui implique que la lumière émise par un gaz est constituée d’un ensemble d’énergies discrètes. Par exemple, lorsqu’une décharge électrique traverse un tube contenant de l’hydrogène gazeux à basse pression, les molécules d’H₂ sont brisées en atomes d’H individus et nous voyons une couleur bleu-rose. Le passage de la lumière à travers un prisme produit un spectre de raies, indiquant que cette lumière est composée de photons de quatre longueurs d’onde visibles, comme le montre la Figure 8.2.2.

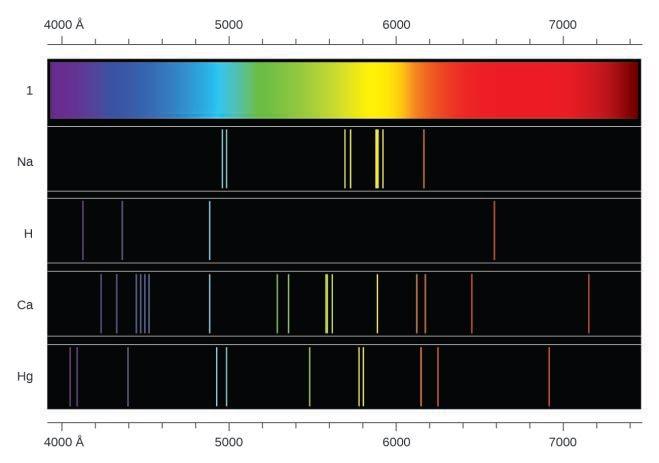
Figure 8.2.2. Comparez les deux types de spectres d’émission : le spectre continu de la lumière blanche (en haut) et les spectres linéaires de la lumière provenant d’atomes de sodium, d’hydrogène, de calcium et de mercure excités.

L’origine des spectres discrets dans les atomes et les molécules était extrêmement déroutante pour les scientifiques à la fin du XIXe siècle, puisque selon la théorie électromagnétique classique, seuls des spectres continus devraient être observés. Plus curieux encore, en 1885, Johann Balmer a pu dériver une équation empirique qui reliait les quatre longueurs d’onde visibles de la lumière émise par les atomes d’hydrogène à des nombres entiers. Cette équation est la suivante, dans laquelle k est une constante :

D’autres raies discrètes pour l’atome d’hydrogène ont été découvertes par la suite dans les régions UV et IR. Johannes Rydberg a généralisé les travaux de Balmer et a développé une formule empirique qui prédit toutes les raies d’émission de l’hydrogène, et pas seulement celles limitées au domaine visible, où, n₁ et n₂ sont des entiers, n₁ < n₂, et R∞ est la constante de Rydberg (1,097 × 10⁷ m^-1).

1 / λ = R_∞((1 / n₁²)- (1 / n₂²))

Équation 8.2.1 Équation de Rydberg

Même à la fin du XIXe siècle, la spectroscopie était une science très précise, et les longueurs d’onde de l’hydrogène étaient donc mesurées avec une très grande précision, ce qui impliquait que la constante de Rydberg pouvait également être déterminée très précisément. Qu’une formule aussi simple que la formule de Rydberg puisse expliquer des mesures aussi précises semblait stupéfiant à l’époque, mais c’est l’explication finale des spectres d’émission par Neils Bohr en 1913 qui a fini par convaincre les scientifiques d’abandonner la physique classique et a stimulé le développement de la mécanique quantique moderne.

Le modèle de Bohr

Suite aux travaux d’Ernest Rutherford et de ses collègues au début du vingtième siècle, l’image d’atomes constitués de noyaux minuscules et denses entourés d’électrons plus légers et encore plus petits se déplaçant continuellement autour du noyau était bien établie. Cette image était appelée le modèle planétaire, car elle représentait l’atome comme un “système solaire” miniature, les électrons tournant autour du noyau comme des planètes autour du soleil. L’atome le plus simple est l’hydrogène, composé d’un seul proton dans le noyau autour duquel se déplace un seul électron. La force électrostatique qui attire l’électron vers le proton ne dépend que de la distance entre les deux particules. La force électrostatique a la même forme que la force gravitationnelle entre deux particules de masse, sauf que la force électrostatique dépend de la magnitude des charges sur les particules (+1 pour le proton et -1 pour l’électron) au lieu de la magnitude des masses des particules qui régissent la force gravitationnelle. Comme les forces peuvent être dérivées des potentiels, il est pratique de travailler avec les potentiels, puisqu’ils sont des formes d’énergie. Le potentiel électrostatique est également appelé potentiel de Coulomb. Comme le potentiel électrostatique a la même forme que le potentiel gravitationnel, selon la mécanique classique, les équations du mouvement devraient être similaires, l’électron se déplaçant autour du noyau sur des orbites circulaires ou elliptiques (d’où l’appellation de modèle “planétaire” de l’atome). Les potentiels de la forme V(r) qui ne dépendent que de la distance radiale r sont appelés potentiels centraux. Les potentiels centraux ont une symétrie sphérique, et donc plutôt que de spécifier la position de l’électron dans les coordonnées cartésiennes habituelles (x, y, z), il est plus pratique d’utiliser des coordonnées polaires sphériques centrées sur le noyau, consistant en une coordonnée linéaire r et deux coordonnées angulaires, généralement spécifiées par les lettres grecques thêta (θ) et phi (Φ). Ces coordonnées sont similaires à celles utilisées dans les appareils GPS et la plupart des smartphones qui suivent les positions sur notre terre (presque) sphérique, avec les deux coordonnées angulaires spécifiées par la latitude et la longitude, et la coordonnée linéaire spécifiée par l’élévation du niveau de la mer. En raison de la symétrie sphérique des potentiels centraux, l’énergie et le moment angulaire de l’atome d’hydrogène classique sont des constantes, et les orbites sont contraintes de se situer dans un plan comme les planètes en orbite autour du soleil. Cette description de l’atome en mécanique classique est cependant incomplète, car un électron se déplaçant sur une orbite elliptique serait en train d’accélérer (en changeant de direction) et, selon l’électromagnétisme classique, il devrait émettre continuellement un rayonnement électromagnétique. Cette perte d’énergie orbitale devrait faire en sorte que l’orbite de l’électron devienne de plus en plus petite jusqu’à ce qu’il s’enfonce dans le noyau, ce qui implique que les atomes sont intrinsèquement instables.

En 1913, Niels Bohr a tenté de résoudre le paradoxe atomique en ignorant la prédiction de l’électromagnétisme classique selon laquelle l’électron en orbite dans l’hydrogène émettrait continuellement de la lumière. Au lieu de cela, il a intégré dans la description de l’atome en mécanique classique les idées de quantification de Planck et la découverte d’Einstein selon laquelle la lumière est constituée de photons dont l’énergie est proportionnelle à leur fréquence. Bohr a supposé que l’électron en orbite autour du noyau n’émettrait normalement aucun rayonnement (hypothèse de l’état stationnaire), mais qu’il émettrait ou absorberait un photon s’il se déplaçait sur une orbite différente. L’énergie absorbée ou émise refléterait les différences entre les énergies orbitales selon cette équation :

|ߡE| = |E_f – E_i| = hv = h(c / λ)

Équation 8.2.2 Différence d’énergie orbitale

Dans cette équation, h est la constante de Planck et E_i et E_f sont les énergies orbitales initiale et finale, respectivement. La valeur absolue de la différence d’énergie est utilisée, puisque les fréquences et les longueurs d’onde sont toujours positives. Au lieu de permettre des valeurs continues pour le moment angulaire, l’énergie et le rayon de l’orbite, Bohr a supposé que seules des valeurs discrètes pouvaient être obtenues (en fait, la quantification de l’une de ces valeurs impliquerait que les deux autres soient également quantifiées). L’expression de Bohr pour les énergies quantifiées est la suivante :

Dans cette expression, k est une constante comprenant des constantes fondamentales telles que la masse et la charge de l’électron et la constante de Planck. En insérant l’expression pour les énergies des orbites dans l’équation pour ΔE, on obtient

Ou

qui est identique à l’équation de Rydberg pour

R_∞ = khc

. Lorsque Bohr a calculé sa valeur théorique pour la constante de Rydberg, R∞, et l’a comparée à la valeur acceptée expérimentalement, il a obtenu un excellent accord. La constante de Rydberg étant l’une des constantes les plus précisément mesurées à l’époque, ce niveau d’accord était étonnant et signifiait que le modèle de Bohr était pris au sérieux, malgré les nombreuses hypothèses dont Bohr avait besoin pour le dériver.

Les quelques niveaux d’énergie les plus bas sont illustrés à la Figure 8.2.3. L’une des lois fondamentales de la physique est que la matière est plus stable avec l’énergie la plus basse possible. Ainsi, l’électron d’un atome d’hydrogène se déplace généralement sur l’orbite n = 1, l’orbite dans laquelle il a la plus faible énergie. Lorsque l’électron se trouve sur cette orbite de plus faible énergie, on dit que l’atome est dans son état électronique fondamental (ou simplement état fondamental). Si l’atome reçoit de l’énergie d’une source extérieure, il est possible que l’électron se déplace vers une orbite avec une valeur n plus élevée et l’atome se trouve alors dans un état électronique excité (ou simplement un état excité) avec une énergie plus élevée.

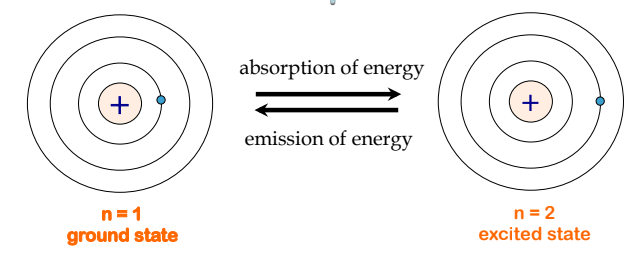
Figure 8.2.3. À gauche, un atome d’hydrogène est représenté dans l’état d’énergie le plus bas, appelé état fondamental, où l’électron se trouve sur l’orbite n = 1. Lorsque l’atome absorbe de l’énergie, l’électron est promu à une orbite supérieure, ce qui donne lieu à un état moins stable et plus énergétique, illustré à droite, appelé état excité. Pour revenir à l’état fondamental, l’atome doit émettre de l’énergie.

Lorsqu’un électron passe d’un état excité (orbite d’énergie supérieure) à un état moins excité, ou état fondamental, la différence d’énergie est émise sous forme de photon. De même, si un photon est absorbé par un atome, l’énergie du photon fait passer un électron d’une orbite de plus basse énergie à une orbite plus excitée. Nous pouvons relater l’énergie des électrons dans les atomes à ce que nous avons appris précédemment sur l’énergie. La loi de la conservation de l’énergie stipule que nous ne pouvons ni créer ni détruire l’énergie. Ainsi, si une certaine quantité d’énergie externe est nécessaire pour exciter un électron d’un niveau d’énergie à un autre, cette même quantité d’énergie sera libérée lorsque l’électron retournera à son état initial (Figure 8.2.2.). En effet, un atome peut ” stocker ” de l’énergie en l’utilisant pour faire passer un électron à un état d’énergie supérieure et la libérer lorsque l’électron revient à un état inférieur. L’énergie peut être libérée sous la forme d’un quantum d’énergie, lorsque l’électron revient à son état fondamental (par exemple, de n = 5 à n = 1), ou elle peut être libérée sous la forme de deux ou plusieurs quanta plus petits lorsque l’électron tombe dans un état intermédiaire, puis dans l’état fondamental (par exemple, de n = 5 à n = 4, en émettant un quantum, puis à n = 1, en émettant un deuxième quantum).

Puisque le modèle de Bohr n’implique qu’un seul électron, il peut également être appliqué aux ions à électron unique He⁺, Li²⁺, Be³⁺, etc., qui ne diffèrent de l’hydrogène que par leur charge nucléaire, de sorte que les atomes et les ions à électron unique sont collectivement appelés atomes de type hydrogène. L’expression de l’énergie des atomes de type hydrogène est une généralisation de l’énergie de l’atome d’hydrogène, dans laquelle Z est la charge nucléaire (+1 pour l’hydrogène, +2 pour He, +3 pour Li, etc.) et k a une valeur de 2,179 × 10^-18 J.

La taille des orbites circulaires des atomes de type hydrogène est donnée en fonction de leur rayon par l’expression suivante, dans laquelle ɑ₀ est une constante appelée rayon de Bohr, dont la valeur est de 5,292 × 10^-11 m :

Équation 8.2.3 Rayon orbital

L’équation nous montre également que lorsque l’énergie de l’électron augmente (lorsque n augmente), l’électron se trouve à une plus grande distance du noyau. C’est ce qu’implique la dépendance inverse de r dans le potentiel de Coulomb, puisque, lorsque l’électron s’éloigne du noyau, l’attraction électrostatique entre lui et le noyau diminue, et il est moins bien maintenu dans l’atome. Notez que plus n est grand et plus les orbites sont grandes, plus leurs énergies se rapprochent de zéro, et donc les limites n ⟶ ∞, et r ⟶ ∞ impliquent que E = 0 correspond à la limite d’ionisation où l’électron est complètement éloigné du noyau. Ainsi, pour l’hydrogène à l’état fondamental n = 1, l’énergie d’ionisation serait :

Trois paradoxes extrêmement déroutants ayant été résolus (le rayonnement du corps noir, l’effet photoélectrique et l’atome d’hydrogène), et tous impliquant la constante de Planck de manière fondamentale, il est devenu évident pour la plupart des physiciens de l’époque que les théories classiques qui fonctionnaient si bien dans le monde macroscopique étaient fondamentalement erronées et ne pouvaient être étendues au domaine microscopique des atomes et des molécules. Malheureusement, malgré la remarquable réussite de Bohr, qui a réussi à trouver une expression théorique pour la constante de Rydberg, il n’a pas pu étendre sa théorie à l’atome le plus simple, l’hydrogène, qui ne possède que deux électrons. Le modèle de Bohr présentait de graves lacunes, car il était encore basé sur la notion d’orbites précises de la mécanique classique, un concept qui s’est avéré par la suite indéfendable dans le domaine microscopique, lorsqu’un modèle approprié de mécanique quantique a été développé pour remplacer la mécanique classique.

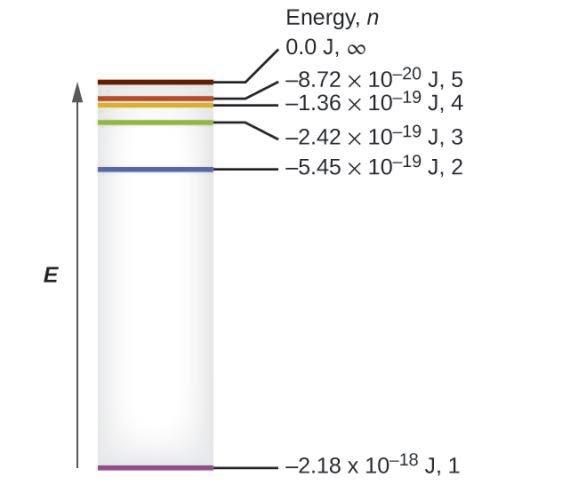
Figure 8.2.4. Nombres quantiques et niveaux d’énergie dans un atome d’hydrogène. Plus la valeur calculée est négative, plus l’énergie est faible.

Exemple 8.2.1 – Calculer l’énergie d’un électron dans une orbite de Bohr

Les premiers chercheurs étaient très enthousiastes lorsqu’ils ont pu prédire l’énergie d’un électron à une distance particulière du noyau d’un atome d’hydrogène. Si une étincelle propulse l’électron d’un atome d’hydrogène sur une orbite avec n = 3, quelle est l’énergie calculée, en joules, de l’électron ?

Solution

L’énergie de l’électron est donnée par cette équation :

Le numéro atomique, Z, de l’hydrogène est 1 ; k = 2,179 × 10^-18 J ; et l’électron est caractérisé par une valeur n de 3. Ainsi,

L’électron de la Figure 8.2.4. est promu encore plus loin sur une orbite avec n = 6. Quelle est sa nouvelle énergie ?

Réponse

−6,053 × 10^–20 J

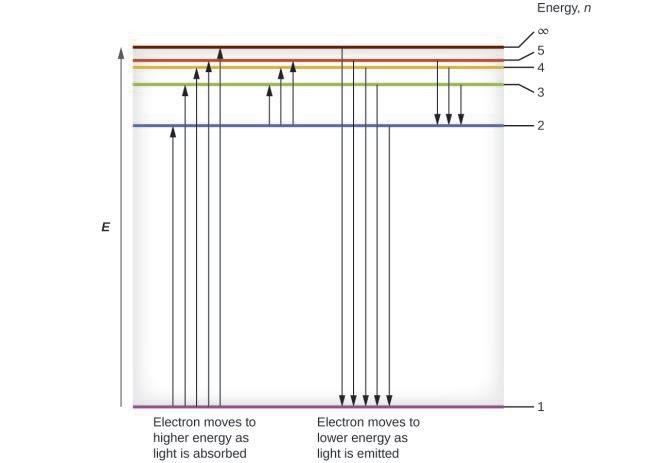
Figure 8.2.4. Les lignes horizontales indiquent l’énergie relative des orbites dans le modèle de Bohr de l’atome d’hydrogène, et les flèches verticales représentent l’énergie des photons absorbés (à gauche) ou émis (à droite) lorsque les électrons se déplacent entre ces orbites.

Exemple 8.2.2 – Calculer l’énergie et la longueur d’onde des transitions d’électron dans un système (Bohr) à un électron

Quelle est l’énergie (en joules) et la longueur d’onde (en mètres) de la raie du spectre de l’hydrogène qui représente le mouvement d’un électron de l’orbite de Bohr avec n = 4 à l’orbite avec n = 6 ? Dans quelle partie du spectre électromagnétique trouve-t-on ce rayonnement ?

Solution

Dans ce cas, l’électron commence avec n = 4, donc n₁ = 4. Il s’immobilise sur l’orbite n = 6, donc n₂ = 6. La différence d’énergie entre les deux états est donnée par cette expression :

Cette différence d’énergie est positive, ce qui indique qu’un photon entre dans le système (est absorbé) pour exciter l’électron de l’orbite n = 4 jusqu’à l’orbite n = 6. La longueur d’onde d’un photon avec cette énergie est trouvée par l’expression

Le réarrangement donne :

D’après la Figure 8.2.1. du concept précédente, nous pouvons voir que cette longueur d’onde se trouve dans la partie infrarouge du spectre électromagnétique.

Vérifiez votre apprentissage 8.2.2 – Calculer l’énergie et la longueur d’onde des transitions d’électron dans un système (Bohr) à un électron

Quelle est l’énergie en joules et la longueur d’onde en mètres du photon produit lorsqu’un électron tombe du niveau n = 5 au niveau n = 3 dans un ion He⁺ (Z = 2 pour He⁺) ?

Réponse

6,198 × 10^-19 J; 3,205 × 10^-7 m

Le modèle de Bohr de l’atome d’hydrogène permet de comprendre le comportement de la matière au niveau microscopique, mais il ne rend pas compte des interactions électron-électron dans les atomes comportant plus d’un électron. Il introduit cependant plusieurs caractéristiques importantes de tous les modèles utilisés pour décrire la distribution des électrons dans un atome. Ces caractéristiques sont les suivantes :

Les énergies des électrons (niveaux d’énergie) dans un atome sont quantifiées, décrites par des nombres quantiques : des nombres entiers n’ayant qu’une valeur spécifique autorisée et utilisés pour caractériser l’arrangement des électrons dans un atome.

L’énergie d’un électron augmente avec la distance qui le sépare du noyau.

Les énergies discrètes (lignes) dans les spectres des éléments résultent d’énergies électroniques quantifiées.

Parmi ces caractéristiques, la plus importante est le postulat des niveaux d’énergie quantifiés pour un électron dans un atome. En conséquence, ce modèle a posé la base du modèle mécanique quantique de l’atome. Bohr a reçu un prix Nobel de physique pour ses contributions à notre compréhension de la structure des atomes et de la manière dont celle-ci est liée aux émissions de spectres de raies.

★ Questions

1. La lumière produite par un panneau au néon rouge est due à l’émission de lumière par des atomes de néon excités. Décrivez qualitativement le spectre produit par le passage de la lumière d’une lampe au néon à travers un prisme.

2. Une ligne violet brillant apparaît à 435,8 nm dans le spectre d’émission de la vapeur de mercure. Quelle quantité d’énergie, en joules, doit être libérée par un électron dans un atome de mercure pour produire un photon de cette lumière?

3. Une lumière d’une longueur d’onde de 614,5 nm a une allure orange.

a) Quelle est l’énergie, en joules, par photon de cette lumière orange ?

b) Quelle est l’énergie en eV (1 eV = 1,602 × 10^-19 J)?

4. Un photon de lumière produit par un laser chirurgical a une énergie de 3,027 × 10^-19 J.

a) Calculez la fréquence et la longueur d’onde du photon.

b) Quelle est l’énergie totale contenue dans 1 mole de photons? 

c) Quelle est la couleur de la lumière émise?

5. Le spectre d’émission du césium contient deux raies dont les fréquences sont (a) 3,45 × 10¹⁴ Hz et (b) 6,53 × 10¹⁴ Hz.

a) Quelles sont les longueurs d’onde et les énergies par photon de ces deux raies ?

b) De quelle couleur sont les raies ?

★★ Questions

6. Les écrans de télévision et d’ordinateur en couleurs RVB utilisent des tubes cathodiques qui produisent des couleurs en mélangeant la lumière rouge, verte et bleue. Si nous regardons l’écran avec une loupe, nous pouvons voir des points individuels s’allumer et s’éteindre au fur et à mesure que les couleurs changent.

a) En utilisant un spectre de lumière visible, déterminez la longueur d’onde approximative de chacune de ces couleurs.

b) Quelle est la fréquence et l’énergie d’un photon de chacune de ces couleurs ?

7.

a) Quelle est la fréquence seuil du sodium métal si un photon de fréquence 6,66 × 10¹⁴ s^-1 éjecte un électron d’énergie cinétique 7,74 × 10^-20 J ?

b) L’effet photoélectrique sera-t-il observé si le sodium est exposé à une lumière orange ?

8. Des atomes de lithium chauffés émettent des photons de lumière d’une énergie de 2,961 × 10^-19 J. Calculez la fréquence et la longueur d’onde de l’un de ces photons.

a) Quelle est l’énergie totale d’une mole de ces photons ?

b) Quelle est la couleur de la lumière émise ?

9. Les photons du rayonnement infrarouge sont responsables d’une grande partie de la chaleur que nous ressentons lorsque nous tenons nos mains devant un feu. Ces photons réchauffent également d’autres objets. Combien de photons infrarouges d’une longueur d’onde de 1,5 × 10^-6 m doivent être absorbés par l’eau pour réchauffer une tasse d’eau (175 g) de 25,0 °C à 40 °C ?

10. Les yeux de certains reptiles transmettent un seul signal visuel au cerveau lorsque les récepteurs visuels sont frappés par des photons d’une longueur d’onde de 850 nm. Si une énergie totale de 3,15 × 10^-14 J est nécessaire pour déclencher le signal, quel est le nombre minimal de photons qui doivent frapper le récepteur ?

Réponses

1. Le spectre est constitué de lignes colorées, dont au moins une (probablement la plus brillante) est rouge.

2. 4.56 x 10^-19 J

3. a) 3.233 × 10⁻¹⁹ J; b) 2.018 eV

4. a) v = 4.568 × 10¹⁴ s; b) λ = 656.3 nm; c) Energy mol⁻¹ = 1.823 × 10⁵ J mol⁻¹; rouge

5. a) λ = 8.69 × 10⁻⁷ m; E = 2.29 × 10⁻¹⁹ J; (b) λ = 4.59 × 10⁻⁷ m; E = 4.33 × 10⁻¹⁹ J; La couleur de (a) est rouge ; (b) est bleue.

6. Rouge : 660 nm; 4,54 × 10¹⁴ Hz; 3,01 × 10^-19 J. Vert : 520 nm; 5,77 × 10¹⁴ Hz; 3,82 × 10^-19 J. Bleu : 440 nm; 6,81 × 10¹⁴ Hz; 4,51 × 10^-19 J. Des nombres légèrement différents sont également possibles.

7. a) 5,49 × 10¹⁴ s^-1; b) non

8. a) Énergie dans 1 mole de photons : 178,3 kJ; b) couleur : rouge

9. 8,3 x 10²² photons

10. 1,3 x 10⁵ photons