8.1 – La nature de la lumière
La nature de la lumière est un sujet de recherche depuis l’Antiquité. Au XVIIe siècle, Isaac Newton a réalisé des expériences avec des lentilles et des prismes et a pu démontrer que la lumière blanche était composée des différentes couleurs de l’arc-en-ciel combinées ensemble. Newton a expliqué ses découvertes en optique par une vision « corpusculaire » de la lumière, selon laquelle la lumière est composée de flux de particules extrêmement minuscules se déplaçant à grande vitesse conformément aux lois du mouvement de Newton. Au XVIIe siècle, d’autres chercheurs, comme Christiaan Huygens, avaient montré que les phénomènes optiques tels que la réflexion et la réfraction pouvaient être tout aussi bien expliqués par la lumière en tant qu’ondes se déplaçant à grande vitesse dans un milieu appelé « éther lumineux », censé imprégner tout l’espace. Au début du XIXe siècle, Thomas Young a démontré que la lumière passant par des fentes étroites et rapprochées produisait des modèles d’interférence qui ne pouvaient pas être expliquées en termes de particules newtoniennes, mais qui pouvaient être facilement expliquées en termes d’ondes. Plus tard au cours du XIXe siècle, après que James Clerk Maxwell eut développé sa théorie du rayonnement électromagnétique et a montré que la lumière était la partie visible d’un vaste spectre d’ondes électromagnétiques, la vision particulaire de la lumière a été totalement discréditée. À la fin du XIXe siècle, les scientifiques considéraient que l’univers physique comprenait grosso modo deux domaines distincts : la matière, composée de particules se déplaçant selon les lois du mouvement de Newton, et le rayonnement électromagnétique, constitué d’ondes régies par les équations de Maxwell. Aujourd’hui, ces domaines sont appelés mécanique classique et électrodynamique classique (ou électromagnétisme classique). Bien que quelques phénomènes physiques n’aient pu être expliqués dans ce cadre, les scientifiques de l’époque étaient si confiants dans la solidité globale de ce cadre qu’ils considéraient ces aberrations comme des paradoxes déroutants qui seraient finalement résolus d’une manière ou d’une autre dans ce cadre. Comme nous le verrons, ces paradoxes ont conduit à un cadre contemporain qui relie intimement les particules et les ondes à un niveau fondamental, appelé dualité onde-particule, qui a supplanté la vision classique.
La lumière visible et d’autres formes de rayonnement électromagnétique jouent un rôle important en chimie, car elles peuvent être utilisées pour déduire l’énergie des électrons dans les atomes et les molécules. Une grande partie de la technologie moderne est basée sur le rayonnement électromagnétique. Par exemple, les ondes radio d’un téléphone portable, les rayons X utilisés par les dentistes, l’énergie utilisée pour cuire les aliments dans votre micro-ondes, la chaleur rayonnante d’objets chauffés au rouge et la lumière de votre écran de télévision sont des formes de rayonnement électromagnétique qui présentent toutes un comportement ondulatoire.
Ondes
Une onde est une oscillation ou un mouvement périodique qui peut transporter de l’énergie d’un point à un autre de l’espace. Des exemples courants d’ondes sont présents tout autour de nous. Secouer l’extrémité d’une corde transfère de l’énergie de votre main à l’autre extrémité de la corde, laisser tomber un caillou dans un étang provoque des ondes à la surface de l’eau, et l’expansion de l’air qui accompagne un éclair génère des ondes sonores (tonnerre) qui peuvent se propager sur plusieurs kilomètres. Dans chacun de ces cas, l’énergie cinétique est transférée à travers la matière (la corde, l’eau ou l’air) alors que la matière reste essentiellement en place. Un exemple perspicace d’onde se produit dans les stades de sport lorsque les supporters d’une zone étroite de sièges se lèvent simultanément et restent debout avec les bras levés pendant quelques secondes avant de se rasseoir, tandis que les supporters des sections voisines se lèvent et s’assoient également dans l’ordre. Bien que cette onde puisse rapidement encercler un grand stade en quelques secondes, aucun des supporters ne se déplace réellement avec l’onde- ils restent tous dans leur siège ou au-dessus.
Les ondes n’ont pas besoin d’être limitées à la traversée de la matière. Comme l’a montré Maxwell, les ondes électromagnétiques sont constituées d’un champ électrique oscillant en phase avec un champ magnétique perpendiculaire, tous deux étant perpendiculaires à la direction du déplacement. Ces ondes peuvent se déplacer dans le vide à une vitesse constante de 2,998 × 108 m/s, la vitesse de la lumière (notée c).
Toutes les ondes, y compris les formes de rayonnement électromagnétique, sont caractérisées par une longueur d'onde (désignée par λ, la lettre grecque minuscule lambda), une fréquence (désignée par ν, la lettre grecque minuscule nu) et une amplitude. Comme on peut le voir sur la Figure 8.1.1., la longueur d’onde est la distance entre deux pics ou creux consécutifs d’une onde (mesurée en mètres dans le système SI). Les ondes électromagnétiques ont des longueurs d’onde qui se situent dans une gamme énorme – des longueurs d’onde de kilomètres (103 m) à picomètres (10-12 m) ont été observées. La fréquence est le nombre de cycles d’ondes qui passent devant un point donné de l’espace en un temps donné (dans le système SI, ce temps est mesuré en secondes). Un cycle correspond à une longueur d’onde complète. L’unité de fréquence, exprimée en cycles par seconde [s-1], est le hertz (Hz). Les multiples courants de cette unité sont le mégahertz (1 MHz = 1 × 106 Hz) et le gigahertz (1 GHz = 1 × 109 Hz). L’amplitude correspond à la magnitude du déplacement de l’onde et donc, dans la Figure 8.1.1., à la moitié de la hauteur entre les pics et les creux. L’amplitude est liée à l’intensité de l’onde, qui est la luminosité pour la lumière et l’intensité sonore pour le son.
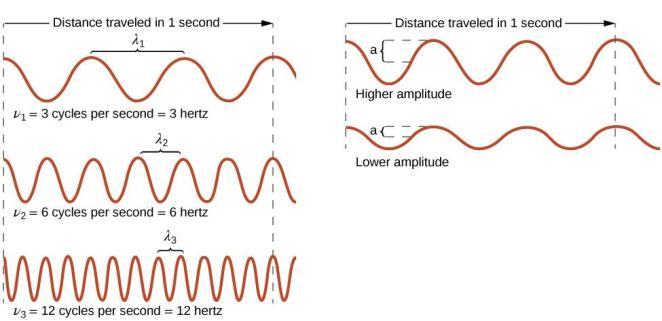
Figure 8.1.1. Les ondes sinusoïdales unidimensionnelles montrent la relation entre la longueur d’onde, la fréquence et la vitesse. L’onde dont la longueur d’onde est la plus courte a la fréquence la plus élevée. L’amplitude est la moitié de la hauteur de l’onde, du sommet au creux.
Le produit de la longueur d’onde (λ) d’une onde par sa fréquence (ν), λν, est la vitesse de l’onde. Ainsi, pour le rayonnement électromagnétique dans le vide :
Équation 8.1.1 Vitesse de la lumière en fonction de sa fréquence et de sa longueur d’onde
La longueur d’onde et la fréquence sont inversement proportionnelles : plus la longueur d’onde augmente, plus la fréquence diminue. La Figure 8.1.2 illustre cette proportionnalité inverse. La Figure 8.1.2. montre également le spectre électromagnétique, c’est-à-dire la gamme de tous les types de rayonnement électromagnétique. Chacune des différentes couleurs de la lumière visible est associée à des fréquences et des longueurs d’onde spécifiques, et vous pouvez constater que la lumière visible ne constitue qu’une petite partie du spectre électromagnétique. Comme les technologies développées pour travailler dans les diverses parties du spectre électromagnétique sont différentes, pour des raisons de commodité et d’héritage historique, on utilise généralement des unités différentes pour les différentes parties du spectre. Par exemple, les ondes radio sont généralement exprimées en fréquences (généralement en MHz), tandis que la région visible est généralement exprimée en longueurs d’onde (généralement en nm ou en angströms).
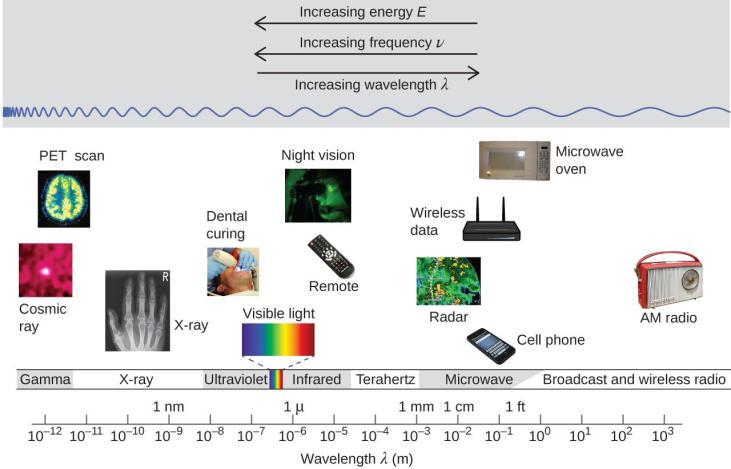
Figure 8.1.2. Les parties du spectre électromagnétique sont représentées par ordre décroissant de fréquence et croissant de longueur d’onde. Parmi les exemples d’applications des différentes longueurs d’onde, citons la tomographie par émission de positons (TEP), l’imagerie à rayons X, les télécommandes, l’Internet sans fil, les téléphones cellulaires et les radios. (crédit « Rayon cosmique » : modification du travail de la NASA ; crédit « Scan PET » : modification du travail du National Institute of Health ; crédit « Rayon X » : modification du travail du Dr. Jochen Lengerke ; crédit « Dental curing » : modification du travail par le Department of the Navy ; crédit « Night vision » : modification du travail par le Département de l’Armée ; crédit « Remote » : modification du travail par Emilian Robert Vicol ; crédit « Cell phone » : modification du travail par Brett Jordan ; crédit « Microwave oven » : modification du travail par Billy Mabray ; crédit « Ultrasound » : modification du travail par Jane Whitney ; crédit « AM radio » : modification du travail par Dave Clausen)
Exemple 8.1.1 – Détermination de la fréquence et de la longueur d’onde des rayonnements
Un lampadaire au sodium émet une lumière jaune dont la longueur d’onde est de 589 nm (1 nm = 1 × 10-9 m). Quelle est la fréquence de cette lumière ?
Solution
Nous pouvons réarranger l’équation c = λν pour résoudre la fréquence :
Comme c est exprimé en mètres par seconde, nous devons également convertir 589 nm en mètres.
Vérifiez votre apprentissage 8.1.1 – Détermination de la fréquence et de la longueur d’onde des rayonnements
L’une des fréquences utilisées pour transmettre et recevoir les signaux des téléphones cellulaires aux États-Unis est de 850 MHz. Quelle est la longueur d’onde en mètres de ces ondes radio ?
Réponse
0,353 m = 35,3 cm
|
Communication sans fil
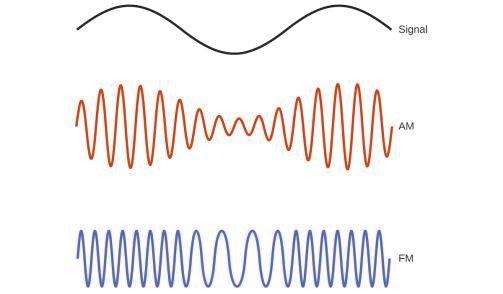
Figure 8.1.3. Les tours radio et cellulaires sont généralement utilisées pour transmettre des rayonnements électromagnétiques de grande longueur d’onde. De plus en plus, les tours cellulaires sont conçues pour se fondre dans le paysage, comme la tour cellulaire de Tucson, Arizona (à droite) déguisée en palmier (crédit à gauche : modification de l’œuvre de Sir Mildred Pierce ; crédit au milieu : modification de l’œuvre de M.O. Stevens). De nombreuses technologies de valeur fonctionnent dans la région des fréquences radio (3 kHz-300 GHz) du spectre électromagnétique. À l’extrémité basse fréquence (faible énergie, grande longueur d’onde) de cette région, se trouvent les signaux radio AM (modulation d’amplitude) (540-2830 kHz) qui peuvent parcourir de longues distances. Les signaux radio FM (modulation de fréquence) sont utilisés à des fréquences plus élevées (87,5-108,0 MHz). En radio AM, l’information est transmise en faisant varier l’amplitude de l’onde (Figure 8.1.4.), tandis que la fréquence est maintenue constante. Dans la radio FM, au contraire, l’amplitude est constante et la fréquence instantanée varie.
Figure 8.1.4. Ce schéma décrit comment la modulation d’amplitude (AM) et la modulation de fréquence (FM) peuvent être utilisées pour transmettre une onde radio. D’autres technologies fonctionnent également dans la partie des ondes radio du spectre électromagnétique. Par exemple, les signaux de téléphonie cellulaire 4G sont d’environ 880 MHz, tandis que les signaux du système de positionnement global (GPS) fonctionnent à 1,228 et 1,575 GHz, les réseaux de technologie sans fil locaux (Wi-Fi) fonctionnent entre 2,4 et 5 GHz, et les capteurs de péage d’autoroute fonctionnent à 5,8 GHz. Les fréquences associées à ces applications sont convenables car ces ondes ont tendance à ne pas être trop absorbées par les matériaux de construction courants.
|
Un phénomène particulièrement caractéristique des ondes se produit lorsque deux ou plusieurs ondes entrent en contact : Elles interfèrent l’une avec l’autre. La Figure 8.1.5. montre les modèles d'interférence qui se produisent lorsque la lumière passe à travers des fentes étroites rapprochées environ d’une longueur d’une onde. Les motifs de franges produits dépendent de la longueur d’onde, les franges étant plus rapprochées pour une lumière de longueur d’onde plus courte passant à travers un ensemble donné de fentes. Lorsque la lumière passe par les deux fentes, chaque fente agit effectivement comme une nouvelle source, ce qui fait que deux ondes très rapprochées entrent en contact au niveau du détecteur (la caméra dans ce cas). Les régions sombres de la Figure 8.1.5. correspondent aux régions où les pics de l’onde provenant d’une fente coïncident avec les creux de l’onde provenant de l’autre fente (interférence destructive), tandis que les régions les plus claires correspondent aux régions où les pics des deux ondes (ou leurs deux creux) coïncident (interférence constructive). De même, lorsque deux pierres sont jetées l’une contre l’autre dans un étang, des modèles d’interférence sont visibles dans les interactions entre les ondes produites par les pierres. De tels modèles d’interférence ne peuvent pas être expliqués par des particules se déplaçant selon les lois de la mécanique classique.

Figure 8.1.5. Des franges d’interférence sont représentées pour la lumière passant par deux fentes étroites et rapprochées. L’espacement des franges dépend de la longueur d’onde, les franges étant plus rapprochées pour la lumière bleue de courte longueur d’onde. (crédit : PASCO)
|
Dorothy Hodgkin Comme les longueurs d’onde des rayons X (10-10 000 picomètres [pm]) sont comparables à la taille des atomes, les rayons X peuvent être utilisés pour déterminer la structure des molécules. Lorsqu’un faisceau de rayons X traverse des molécules regroupées dans un cristal, les rayons X entrent en collision avec les électrons et se dispersent. Les interférences constructives et destructives de ces rayons X diffusés créent un modèle de diffraction spécifique. En calculant à rebours à partir de ce schéma, on peut déterminer très précisément la position de chacun des atomes de la molécule. L’une des pionnières qui a contribué à créer cette technologie est Dorothy Crowfoot Hodgkin. Elle est née au Caire, en Égypte, en 1910, où ses parents britanniques étudiaient l’archéologie. Dès son plus jeune âge, elle est fascinée par les minéraux et les cristaux. Lorsqu’elle était étudiante à l’université d’Oxford, elle a commencé à chercher comment la cristallographie aux rayons X pouvait être utilisée pour déterminer la structure des biomolécules. Elle a inventé de nouvelles techniques qui lui ont permis, ainsi qu’à ses étudiants, de déterminer la structure de la vitamine B12, de la pénicilline et de nombreuses autres molécules importantes. Le diabète, une maladie qui touche 382 millions de personnes dans le monde, fait intervenir l’hormone insuline. Hodgkin a commencé à étudier la structure de l’insuline en 1934, mais il a fallu plusieurs décennies de progrès dans le domaine pour qu’elle fasse enfin état de la structure en 1969. La compréhension de la structure a permis de mieux comprendre la maladie et les options de traitement. |
Toutes les ondes ne sont pas des ondes progressives. Les ondes stationnaires restent confinées dans une certaine région de l’espace. Comme nous le verrons, les ondes stationnaires jouent un rôle important dans notre compréhension de la structure électronique des atomes et des molécules. L’exemple le plus simple d’une onde stationnaire est une onde unidimensionnelle associée à une corde vibrante maintenue fixe à ses deux extrémités. La Figure 8.1.6. montre les quatre ondes stationnaires de plus basse énergie (l’onde fondamentale et les trois harmoniques les plus basses) pour une corde vibrante à une amplitude particulière. Bien que le mouvement de la corde se situe principalement dans un plan, l’onde elle-même est considérée comme unidimensionnelle, puisqu’elle se situe dans le sens de la longueur de la corde. Le mouvement des segments de corde dans une direction perpendiculaire à la longueur de la corde génère les ondes. L’amplitude des ondes est donc visible en tant que déplacement maximal des courbes, comme le montre la Figure 8.1.6. L’observation clé de cette figure est que seules les ondes ayant un nombre entier, n, de demi-longueurs d’onde entre les points d’extrémité peuvent se former. Un système avec des points d’extrémité fixes comme celui-ci limite le nombre et le type de formes d’onde possibles. Il s’agit d’un exemple de quantification, dans lequel seules les valeurs discrètes d’un ensemble plus général de valeurs continues d’une propriété sont observées. Une autre observation importante est que les ondes harmoniques (les ondes affichant plus d’une demi-longueur d’onde) ont toutes un ou plusieurs points entre les deux extrémités qui ne sont pas en mouvement. Ces points particuliers sont des nœuds. Les énergies des ondes stationnaires d’une amplitude donnée dans une corde vibrante augmentent avec le nombre de demi-longueurs d’onde n. Le nombre de nœuds étant égal à n – 1, on peut également dire que l’énergie dépend du nombre de nœuds, augmentant généralement à mesure que le nombre de nœuds augmente.

Figure 8.1.6. Une corde vibrante présente des ondes stationnaires unidimensionnelles. Comme les deux extrémités de la corde sont fixes, seules des ondes ayant un nombre entier de demi-longueurs d’onde peuvent se former. Les points de la corde situés entre les extrémités qui ne bougent pas sont appelés les nœuds.
Un exemple d’ondes stationnaires bidimensionnelles est illustré à la Figure 8.1.7. qui montre les motifs vibratoires sur une surface plane. Bien qu’il soit impossible de voir les amplitudes vibratoires comme dans le cas de la corde vibrante, les nœuds ont été rendus visibles en saupoudrant la surface du tambour d’une poudre qui s’accumule sur les zones de la surface dont le déplacement est minimal. Pour les ondes stationnaires unidimensionnelles, les nœuds étaient des points sur la ligne, mais pour les ondes stationnaires bidimensionnelles, les nœuds sont des lignes sur la surface (pour les ondes stationnaires tridimensionnelles, les nœuds sont des surfaces bidimensionnelles dans le volume tridimensionnel).
En raison de la symétrie circulaire de la surface du tambour, ses conditions limites (la surface du tambour étant étroitement contrainte à la circonférence du tambour) donnent lieu à deux types de nœuds : les nœuds radiaux qu’étendent tous les angles à des rayons constants et sont donc considérés comme des cercles autour du centre, et les nœuds angulaires qu’étendent tous les rayons à des angles constants et sont donc considérés comme des lignes passant par le centre. L’image supérieure gauche de la Figure 8.1.7. montre deux nœuds radiaux, tandis que l’image inférieure droite montre le modèle vibratoire associé à trois nœuds radiaux et deux nœuds angulaires.

Figure 8.1.7. Des ondes stationnaires bidimensionnelles peuvent être visualisées sur une surface vibrante. La surface a été saupoudrée d’une poudre qui s’accumule près des lignes nodales. Deux types de nœuds sont visibles : les nœuds radiaux (cercles) et les nœuds angulaires (rayons).
Vous pouvez observer la formation de divers nœuds radiaux ici, alors que la chanteuse Imogen Heap projette sa voix sur une timbale.
Les dernières décennies du XIXe siècle ont été marquées par une intense activité de recherche visant à commercialiser l’éclairage électrique nouvellement découvert. Il fallait pour cela obtenir une meilleure compréhension des distributions de la lumière émise par les diverses sources envisagées. L’éclairage artificiel est généralement conçu pour imiter la lumière naturelle du soleil dans les limites de la technologie sous-jacente. Un tel éclairage consiste d’une gamme de fréquences largement distribuées qui forment un spectre continu. La Figure 8.1.8. montre la distribution des longueurs d’onde de la lumière solaire. Le rayonnement le plus intense se trouve dans la région visible, l’intensité diminuant rapidement pour la lumière ultraviolette (UV) de longueur d’onde plus courte, et plus lentement pour la lumière infrarouge (IR) de longueur d’onde plus grande.
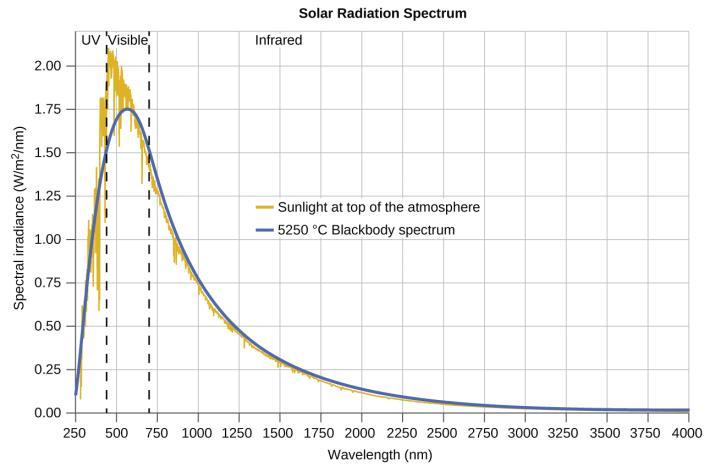
Figure 8.1.8. La distribution spectrale (intensité lumineuse en fonction de la longueur d’onde) de la lumière solaire qui atteint l’atmosphère terrestre sous forme de lumière UV, de lumière visible et de lumière IR. La lumière solaire non absorbée au sommet de l’atmosphère a une distribution qui correspond approximativement à la distribution théorique d’un corps noir à 5250 °C, représentée par la courbe bleue. (crédit : modification du travail de l’American Society for Testing and Materials (ASTM) Terrestrial Reference Spectra for Photovoltaic Performance Evaluation)
Dans la Figure 8.1.9., la distribution solaire est comparée à une distribution représentative, appelée spectre du corps noir, qui correspond à une température de 5250 °C. Le spectre du corps noir correspond assez bien au spectre solaire. Un corps noir est un émetteur idéal pratique qui se rapproche du comportement de nombreux matériaux lorsqu’ils sont chauffés. Il est « idéal » dans le même sens qu’un gaz idéal est une représentation simple et pratique de gaz réels qui fonctionne bien, à condition que la pression ne soit pas trop élevée et la température trop basse. Une bonne approximation d’un corps noir qui peut être utilisée pour observer le rayonnement du corps noir est un four métallique qui peut être chauffé à de très hautes températures. Le four comporte un petit trou permettant d’observer la lumière émise dans le four à l’aide d’un spectromètre afin de mesurer les longueurs d’onde et leurs intensités. La Figure 8.1.9. montre les courbes résultantes pour quelques températures représentatives. Chaque distribution ne dépend que d’un seul paramètre : la température. Les maxima des courbes de corps noir, λmax, se déplacent vers des longueurs d’onde plus courtes au fur et à mesure que la température augmente, reflétant l’observation selon laquelle les métaux chauffés à haute température commencent à briller d’un rouge plus sombre qui devient plus brillant au fur et à mesure que la température augmente, pour finalement devenir blanc à très haute température, lorsque les intensités de toutes les longueurs d’onde visibles deviennent appréciables. Cette observation commune était au cœur du premier paradoxe qui a montré les limites fondamentales de la physique classique que nous allons examiner.
Les physiciens ont dérivé des expressions mathématiques pour les courbes du corps noir en utilisant des concepts bien acceptés des théories de la mécanique classique et de l’électromagnétisme classique. Les expressions théoriques en fonction de la température s’adaptaient bien aux courbes expérimentales du corps noir pour les grandes longueurs d’onde, mais présentaient des divergences importantes pour les longueurs d’onde plus courtes. Non seulement les courbes théoriques ne présentaient pas de pic, mais elles montraient de manière absurde que l’intensité devenait infiniment grande à mesure que la longueur d’onde diminuait, ce qui impliquait que les objets quotidiens à température ambiante devaient émettre de grandes quantités de lumière UV. Cette situation a été appelée la « catastrophe de l’ultraviolet », car personne n’a pu trouver de problème dans le traitement théorique qui aurait pu conduire à un comportement aussi irréaliste pour les courtes longueurs d’onde. Enfin, vers 1900, Max Planck a dérivé une expression théorique pour le rayonnement du corps noir qui correspondait exactement aux observations expérimentales (dans les limites de l’erreur expérimentale). Planck a développé son traitement théorique en étendant les travaux antérieurs qui avaient été basés sur le principe que les atomes composant le four vibraient à des fréquences croissantes (ou à des longueurs d’onde décroissantes) à mesure que la température augmentait, ces vibrations étant la source du rayonnement électromagnétique émis. Mais alors que les traitements précédents avaient permis aux atomes vibrants d’avoir n’importe quelle valeur d’énergie obtenue à partir d’un ensemble continu d’énergies (parfaitement raisonnable, selon la physique classique), Planck a découvert qu’en limitant les énergies vibratoires à des valeurs discrètes pour chaque fréquence, il pouvait dériver une expression pour le rayonnement du corps noir dont l’intensité chutait rapidement pour les courtes longueurs d’onde dans la région UV.
La quantité h est une constante désormais connue sous le nom de constante de Planck, en son honneur. Bien que Planck soit heureux d’avoir résolu le paradoxe du rayonnement du corps noir, il était troublé par le fait que, pour ce faire, il devait supposer que les atomes vibrants avaient besoin d’énergies quantifiées, ce qu’il était incapable d’expliquer. La valeur de la constante de Planck est très faible, 6,626 × 10-34 joules secondes (J s), ce qui contribue à expliquer pourquoi la quantification de l’énergie n’avait pas été observée auparavant dans les phénomènes macroscopiques.
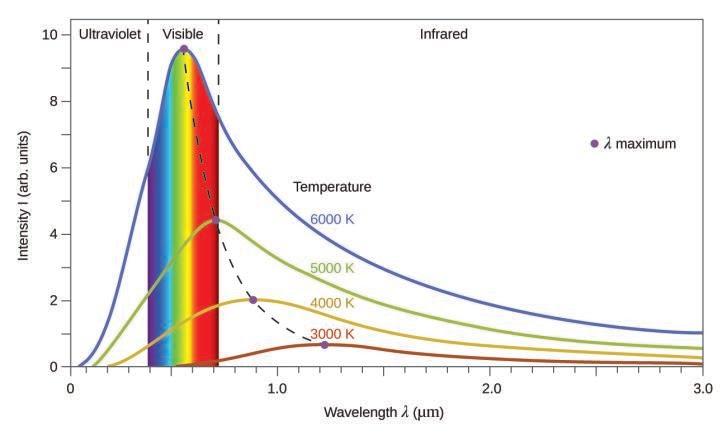
Figure 8.1.9. Les courbes de distribution spectrale du corps noir sont présentées pour quelques températures représentatives.
L’effet photoélectrique
Le prochain paradoxe de la théorie classique à résoudre concernait l’effet photoélectrique (Figure 8.1.10.). On avait observé que des électrons pouvaient être éjectés de la surface propre d’un métal lorsque de la lumière ayant une fréquence supérieure à une certaine fréquence seuil était projetée sur celui-ci. Étonnamment, l’énergie cinétique des électrons éjectés ne dépendait pas de la luminosité de la lumière, mais augmentait avec la fréquence de la lumière. Comme les électrons du métal avaient une certaine énergie de liaison qui les retenait, la lumière incidente devait avoir plus d’énergie pour libérer les électrons. Selon la théorie classique des ondes, l’énergie d’une onde dépend de son intensité (qui dépend de son amplitude), et non de sa fréquence. Ces observations ont notamment permis de constater que le nombre d’électrons éjectés dans une période de temps donné augmentait avec la luminosité. En 1905, Albert Einstein a pu résoudre le paradoxe en incorporant les résultats de la quantification de Planck dans la vision particulaire discréditée de la lumière (Einstein a en fait reçu son prix Nobel pour ce travail, et non pour ses théories de la relativité pour lesquelles il est le plus célèbre).
Einstein a fait valoir que les énergies quantifiées que Planck avait postulées dans son traitement du rayonnement du corps noir pouvaient être appliquées à la lumière dans l’effet photoélectrique, de sorte que la lumière frappant la surface métallique ne devait pas être considérée comme une onde, mais plutôt comme un flux de particules (appelées plus tard photons) dont l’énergie dépendait de leur fréquence, selon la formule de Planck, E = hν (ou, en termes de longueur d’onde, en utilisant c = νλ,
). Les électrons étaient éjectés lorsqu’ils étaient frappés par des photons ayant une énergie suffisante (une fréquence supérieure au seuil). Plus la fréquence est élevée, plus l’énergie cinétique communiquée aux électrons qui s’échappent par les collisions est importante. Einstein a également affirmé que l’intensité de la lumière ne dépendait pas de l’amplitude de l’onde entrante, mais correspondait plutôt au nombre de photons frappant la surface dans une période de temps donné. Cela explique pourquoi le nombre d’électrons éjectés augmentait avec la luminosité, puisque plus le nombre de photons entrants était élevé, plus la probabilité qu’ils entrent en collision avec certains des électrons était grande.
Avec les découvertes d’Einstein, la nature de la lumière a pris un nouvel air de mystère. Bien que de nombreux phénomènes lumineux puissent être expliqués en termes d’ondes ou de particules, certains phénomènes, comme les modèles d’interférence obtenues lorsque la lumière traverse une double fente, sont totalement contraires à une vision particulaire de la lumière, tandis que d’autres phénomènes, comme l’effet photoélectrique, sont totalement contraires à une vision ondulatoire de la lumière. D’une manière ou d’une autre, à un niveau fondamental profond encore mal compris, la lumière est à la fois une onde et une particule. C’est ce qu’on appelle la dualité onde-particule.
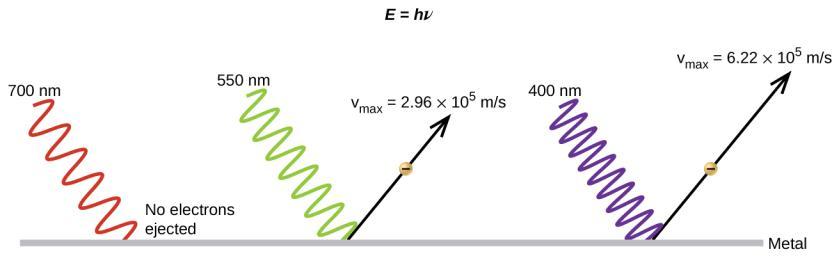
Figure 8.1.10. Les photons de basse fréquence n’ont pas assez d’énergie pour provoquer l’éjection d’électrons par effet photoélectrique. Pour toute fréquence de lumière supérieure à la fréquence seuil, l’énergie cinétique d’un électron éjecté augmente linéairement avec l’énergie du photon entrant.
Exemple 8.1.2 – Calculer l’énergie des radiations
Lorsque nous voyons la lumière d’un panneau au néon, nous observons le rayonnement d’atomes de néon excités. Si cette radiation a une longueur d’onde de 640 nm, quelle est l’énergie du photon émis ?
Solution
Nous utilisons la partie de l’équation de Planck qui inclut la longueur d’onde, λ, et convertissons les unités de nanomètres en mètres afin que les unités de λ et de c soient les mêmes.
Vérifiez votre apprentissage 8.1.2 – Calculer l’énergie des radiations
Les micro-ondes d’un four ont une fréquence spécifique qui chauffe les molécules d’eau contenues dans les aliments (c’est pourquoi la plupart des plastiques et du verre ne deviennent pas chauds dans un four à micro-ondes – ils ne contiennent pas de molécules d’eau). Cette fréquence est d’environ 3 × 109 Hz. Quelle est l’énergie d’un photon dans ces micro-ondes ?
Réponse
2 × 10-24 J
Utilisez ce programme de simulation pour expérimenter l’effet photoélectrique et voir comment l’intensité, la fréquence, le type de métal et d’autres facteurs influencent les photons éjectés.
Exemple 8.1.3 – Effet photoélectrique
Identifiez les affirmations suivantes qui sont fausses et, si nécessaire, modifiez le mot ou la phrase en italique pour les rendre vraies, conformément à l’explication de l’effet photoélectrique par Einstein.
(a) L’augmentation de la luminosité de la lumière entrante augmente l’énergie cinétique des électrons éjectés.
(b) L’augmentation de la longueur d’onde de la lumière entrante augmente l’énergie cinétique des électrons éjectés.
(c) L’augmentation de la luminosité de la lumière entrante augmente le nombre d’électrons éjectés.
(d) L’augmentation de la fréquence de la lumière entrante peut augmenter le nombre d’électrons éjectés.
Solution
(a) Faux. L’augmentation de la luminosité de la lumière entrante n’a aucun effet sur l’énergie cinétique des électrons éjectés. Seule l’énergie, et non le nombre ou l’amplitude, des photons influence l’énergie cinétique des électrons.
(b) Faux. L’augmentation de la fréquence de la lumière entrante augmente l’énergie cinétique des électrons éjectés. La fréquence est proportionnelle à l’énergie et inversement proportionnelle à la longueur d’onde. Les fréquences supérieures à la valeur seuil transfèrent l’excès d’énergie dans l’énergie cinétique des électrons.
(c) Vrai. Comme le nombre de collisions avec les photons augmente avec une lumière plus intense, le nombre d’électrons éjectés augmente.
(d) Vrai en ce qui concerne le seuil d’énergie liant les électrons au métal. En dessous de ce seuil, les électrons ne sont pas émis et au-dessus, ils le sont. Une fois le seuil dépassé, une augmentation supplémentaire de la fréquence n’augmente pas le nombre d’électrons éjectés.
Vérifiez votre apprentissage 8.1.3 – Effet photoélectrique
Calculez l’énergie de seuil en kJ/mol des électrons dans l’aluminium, sachant que le photon de fréquence la plus basse pour lequel l’effet photoélectrique est observé est de 9,87 × 1014 Hz.
Réponse
394 kJ/mol
★ Questions
1. Décrivez les caractéristiques d’une onde lumineuse.
2. Quelle est la fréquence (en s-1) de la lumière si sa longueur d’onde est de 7,33 × 10-5 m ?
3. Quelle est la fréquence (en s-1) de la lumière si sa longueur d’onde est de 733 nm ?
4. Quelle est la longueur d’onde (en mètres) de la lumière si sa fréquence est de 8,19 × 1014 s-1 ?
5. Quelle est la longueur d’onde (en mètres) de la lumière si sa fréquence est de 1,009 × 106 Hz ?
6. Quelle est l’énergie (en joules) d’un photon si sa fréquence est de 5,55 × 1013 s-1 ?
7. Quelle est l’énergie (en joules) d’un photon si sa longueur d’onde est de 5,88 × 10-4 m ?
8. Alors que l’agent de police rédigeait votre contravention pour excès de vitesse, il a mentionné qu’il utilisait un pistolet radar ultramoderne fonctionnant à 35,5 GHz. Quelle est la longueur d’onde du rayonnement émis par le pistolet radar (en millimètres) ?
9. Votre station de radio FM préférée, WXYZ, émet à une fréquence de 101,1 MHz. Quelle est la longueur d’onde de ce rayonnement (en mètres) ?
Réponses
1. La lumière a une longueur d’onde et une fréquence.
2. 4,09 × 1012 s−1
3. 4,09 × 1014 s−1
4. 3,66 × 10−7 m
5. 297 m
6. 3,68 × 10−20 J
7. 3,38 × 10−22 J
8. 8,45 mm
9. 2,965 m
Énergie transmise par des ondes qui ont une composante de champ électrique et une composante de champ magnétique
Distance entre deux pics ou creux consécutifs (ou autres points correspondants) dans une vague
Distance entre deux pics ou creux consécutifs (ou autres points correspondants) dans une vague
Nombre de cycles d'ondes (pics ou creux) qui passent par un point donné dans l'espace par unité de temps
Ampleur du déplacement de la vague, correspondant à la moitié de la hauteur entre les pics et les creux ; liée à l'intensité d'une vague
Unité de fréquence, qui est le nombre de cycles par seconde, s-1
La gamme complète des longueurs d'onde, des fréquences et des énergies possibles que peut comporter le rayonnement électromagnétique, y compris les radiations, les micro-ondes, les infrarouges, le visible, l'ultraviolet, les rayons X et les rayons gamma
Motif généralement constitué d'une alternance de franges claires et sombres ; il résulte de l'interférence constructive et destructive des ondes
Phénomène d'onde localisé caractérisé par des longueurs d'onde discrètes déterminées par les conditions limites utilisées pour générer les ondes ; les ondes stationnaires sont intrinsèquement quantifiées
Limitation de certains biens à des valeurs discrètes spécifiques, non continues
Tout point d'une onde stationnaire d'amplitude nulle
Rayonnement électromagnétique émis dans une série ininterrompue de longueurs d'onde, contenant toutes les couleurs de lumière (par exemple, la lumière blanche du soleil)
Absorbeur parfait idéalisé de tous les rayonnements électromagnétiques incidents ; ces corps émettent des rayonnements électromagnétiques dans des spectres continus caractéristiques appelés rayonnements de corps noirs
Le plus petit paquet discret possible de rayonnement électromagnétique, une particule de lumière
Observation que les particules élémentaires peuvent présenter à la fois des propriétés ondulatoires et particulaires