7.7 – Mécanismes de Réaction

Réactions élémentaires unimoléculaires

La molécularité d’une réaction élémentaire est le nombre d’espèces réactives (atomes, molécules ou ions). Par exemple, une réaction unimoléculaire implique le réarrangement d’une seule espèce réactive pour produire une ou plusieurs molécules de produit:

A → produits

L’équation de vitesse pour une réaction unimoléculaire est:

vitesse = k[A]

Une réaction unimoléculaire peut être l’une des nombreuses réactions élémentaires d’un mécanisme complexe. Par exemple, la réaction:

O₃ → O₂ + O

illustre une réaction élémentaire unimoléculaire qui se produit dans le cadre d’un mécanisme réactionnel à deux étapes. Cependant, certaines réactions unimoléculaires peuvent n’avoir qu’une seule réaction dans le mécanisme réactionnel. (En d’autres termes, une réaction élémentaire peut également être une réaction globale dans certains cas). Par exemple, la décomposition en phase gazeuse du cyclobutane, C₄H₈, en éthylène, C₂H₄, se produit par un mécanisme unimoléculaire à une seule étape:

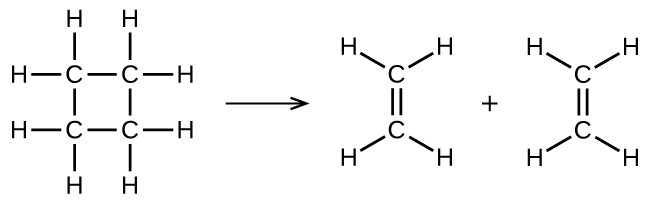
Pour que ces réactions unimoléculaires se produisent, il suffit que des parties de molécules réactives uniques soient séparées en produits.

Les liaisons chimiques ne se brisent pas simplement au cours des réactions chimiques. De l’énergie est nécessaire pour rompre les liaisons chimiques. L’énergie d’activation pour la décomposition du C4H8, par exemple, est de 261 kJ par mole. Cela signifie qu‘il faut 261 kilojoules pour déformer une mole de ces molécules en complexes activés qui se décomposent en produits:

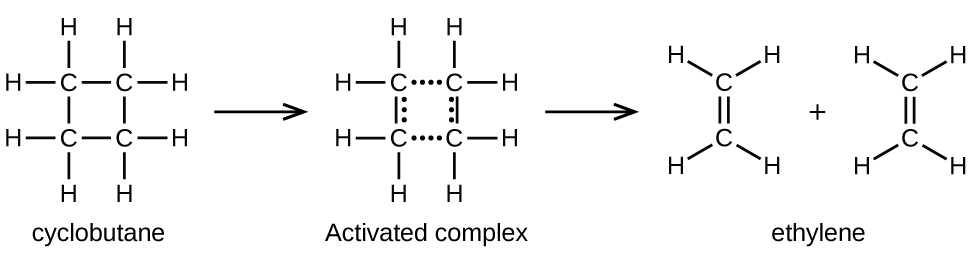
Dans un échantillon de C4H8, quelques-unes des molécules de C4H8 qui se déplacent rapidement entrent en collision avec d’autres molécules qui se déplacent rapidement et prennent de l’énergie supplémentaire. Lorsque les molécules de C4H8 gagnent suffisamment d’énergie, elles peuvent se transformer en un complexe activé, et la formation de molécules d’éthylène peut se produire. En effet, une collision particulièrement énergétique fait tomber une molécule de C4H8 dans la géométrie du complexe activé. Cependant, seule une petite fraction des molécules de gaz se déplacent à des vitesses suffisamment élevées avec des énergies cinétiques suffisamment grandes pour accomplir cela. Par conséquent, à tout moment, seules quelques molécules reçoivent suffisamment d’énergie des collisions pour réagir.

La vitesse de décomposition du C4H8 est directement proportionnelle à sa concentration. Si l’on double la concentration de C4H8 dans un échantillon, on obtient deux fois plus de molécules par litre. Bien que la fraction de molécules ayant suffisamment d’énergie pour réagir reste la même, le nombre total de ces molécules est deux fois plus important. Par conséquent, il y a deux fois plus de C4H8 par litre, et la vitesse de réaction est deux fois plus rapide:

vitesse = -Δ[C₄H₈]Δt = k[C₄H₈]

Une relation similaire s’applique à toute réaction élémentaire unimoléculaire; la vitesse de réaction est directement proportionnelle à la concentration du réactif, et la réaction présente un comportement du premier ordre. La constante de proportionnalité est la constante de vitesse de la réaction unimoléculaire particulière.

Réactions élémentaires bimoléculaires

La collision et la combinaison de deux molécules ou atomes pour former un complexe activé dans une réaction élémentaire est appelée [pb_glossary id=”1939″]réaction bimoléculaire[/pb_glossary]. Il existe deux types de réactions élémentaires bimoléculaires:

A + B  →  produits

et

2A  →  produits

Pour le premier type, dans lequel les deux molécules réactives sont différentes, la loi de vitesse est du premier ordre en A et du premier ordre en B:

vitesse = k[A][B]

Pour le second type, dans lequel deux molécules identiques entrent en collision et réagissent, la loi de vitesse est du second ordre en A:

vitesse = k[A][A] = k[A]²

Certaines réactions chimiques ont des mécanismes qui consistent en une seule réaction élémentaire bimoléculaire. Un exemple est la réaction du dioxyde d’azote avec le monoxyde de carbone:

NO₂ (g) + CO (g) → NO (g) + CO₂ (g)

Une autre est la décomposition de deux molécules d’iodure d’hydrogène pour produire de l’hydrogène, H₂, et de l’iode, I₂ Figure 7.7.1.:

2HI (g) → H₂ (g) + I₂ (g)

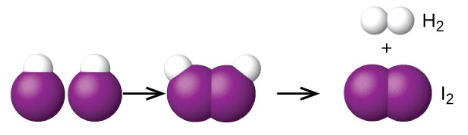
Deux molécules HI – État de transition – Les molécules d’iodure d’hydrogène se décomposent pour produire de l’hydrogène H₂ et l’iode I₂

Figure 7.7.1. Mécanisme probable de la dissociation de deux molécules de HI pour produire une molécule de H₂ et une molécule de I₂.

Les réactions élémentaires bimoléculaires peuvent également intervenir en tant qu’étapes dans un mécanisme réactionnel à plusieurs étapes. La réaction de l’oxygène atomique avec l’ozone en est un exemple:

O (g) + O₃ (g)  →  2O₂ (g)

Réactions élémentaires termoléculaires

Une réaction termoléculaire élémentaire implique la collision simultanée de trois atomes, molécules ou ions. Les réactions élémentaires termoléculaires sont peu fréquentes car la probabilité que trois particules entrent en collision simultanément est inférieure à un millième de la probabilité que deux particules entrent en collision. Il existe cependant quelques réactions élémentaires termoléculaires établies. La réaction de l’oxyde nitrique avec l’oxygène semble impliquer des étapes termoléculaires:

2NO + O₂  →  2NO₂

vitesse = k[NO]2 [O₂]

De même, la réaction de l’oxyde nitrique avec le chlore semble impliquer des étapes termoléculaires:

2NO + Cl₂  →  2NOCl

vitesse = k[NO]2[Cl₂]

Relier les mécanismes de réaction aux lois de vitesse

Il arrive souvent qu’une étape d’un mécanisme de réaction à plusieurs étapes soit nettement plus lente que les autres. Comme une réaction ne peut pas se dérouler plus rapidement que son étape la plus lente, cette étape limite la vitesse à laquelle la réaction globale se produit. L’étape la plus lente est donc appelée étape limitant (ou étape déterminant la vitesse) de la réaction Figure 7.7.2.

Figure 7.7.2. Une cage à bétail est un exemple non chimique d’une étape déterminant la vitesse. Le bétail ne peut être déplacé d’un enclos à un autre qu’aussi rapidement qu’un animal peut passer par la chute. (crédit: Loren Kerns)

Comme décrit précédemment, les lois de vitesse peuvent être dérivées directement des équations chimiques pour les réactions élémentaires. Ce n’est cependant pas le cas pour les réactions chimiques ordinaires. Les équations équilibrées que l’on rencontre le plus souvent représentent le changement global d’un certain système chimique, et très souvent, il s’agit du résultat de certains mécanismes de réaction à plusieurs étapes. Dans tous les cas, nous devons déterminer la loi de vitesse globale à partir de données expérimentales et déduire le mécanisme de la loi de vitesse (et parfois d’autres données). La réaction de NO₂ et de CO fournit un exemple illustratif:

NO₂ (g) + CO (g) → CO₂ (g) + NO (g)

Pour les températures supérieures à 225 °C, la loi de vitesse a été trouvée comme étant:

vitesse = k[NO₂][CO]

La réaction est du premier ordre en ce qui concerne le NO₂ et du premier ordre en ce qui concerne le CO. Ceci est cohérent avec un mécanisme bimoléculaire à une seule étape et il est possible que ce soit le mécanisme de cette réaction à haute température.

À des températures inférieures à 225 °C, la réaction est décrite par une loi de vitesse qui est du second ordre par rapport au NO₂:

vitesse = k[NO₂]²

Ceci est cohérent avec un mécanisme qui implique les deux réactions élémentaires suivantes, dont la première est plus lente et constitue donc l’étape déterminant la vitesse:

NO₂ (g) + NO₂ (g)  →  NO₃ (g) + NO (g) (lent)

NO₃ (g) + CO (g)  →  NO₂ (g) + CO₂ (g) (rapide)

L’étape déterminant la vitesse donne une loi de vitesse montrant une dépendance du second ordre par rapport à la concentration de NO₂, et la somme des deux équations donne la réaction globale nette.

En général, lorsque l’étape déterminant la vitesse (plus lente) est la première étape d’un mécanisme, la loi de vitesse de la réaction globale est la même que la loi de vitesse de cette étape. Cependant, lorsque l’étape déterminant la vitesse est précédée d’une étape impliquant une réaction d’équilibre, la loi de vitesse de la réaction globale peut être plus difficile à dériver. Afin de résoudre ce type d’équation de vitesse, la méthode utilisée est appelée pré-équilibre.

Une réaction élémentaire est à l’équilibre lorsqu’elle se déroule à vitesse égale dans le sens direct et dans le sens inverse. Considérons la dimérisation de NO en N₂O₂, avec k₁ utilisé pour représenter la constante de vitesse de la réaction directe et k_-1 utilisé pour représenter la constante de vitesse de la réaction inverse:

NO + NO  ⇌  N₂O₂

vitesse_directe = vitesse_inverse

k₁[NO]² = k_-1 [N₂O₂]

Si le N₂O₂ était un intermédiaire dans un mécanisme, cette expression pourrait être réarrangée pour représenter la concentration de N₂O₂ dans l’expression de la loi de vitesse globale en utilisant une manipulation algébrique:

k₁[NO]² k_-1=[N2O2]

Cependant, une fois encore, les intermédiaires ne peuvent pas être classés comme faisant partie de l’expression de la loi de vitesse globale, bien qu’ils puissent être inclus dans une réaction élémentaire individuelle d’un mécanisme. L’exemple suivant illustre comment dériver des lois de vitesse globale à partir de mécanismes impliquant des étapes d’équilibre précédant l’étape déterminant la vitesse.

Exemple 7.7.2 (en utilisant le pré–équilibre) – Détermination de l’expression de la loi de vitesse globale pour un mécanisme de réaction à plusieurs étapes

Le chlorure de nitrile (NO₂Cl) se décompose en dioxyde d’azote (NO₂) et en chlore gazeux (Cl₂) selon le mécanisme suivant:

2NO₂Cl (g)  ⇌  ClO₂ (g) + N₂O (g) + ClO (g) (rapide, k₁ représente la constante de vitesse pour la réaction directe et k_-1 la constante de vitesse pour la réaction inverse).

N₂O (g) + ClO₂ (g)  ⇌  NO₂ (g) + NOCl (g) (rapide, k₂ pour la réaction directe, k_-2 pour la réaction inverse)

NOCl + ClO  →  NO₂ + Cl₂ (lent, k₃ la constante de vitesse pour la réaction directe)

Déterminez la réaction globale, écrivez l’expression de la loi de vitesse pour chaque réaction élémentaire, identifiez tout intermédiaire et déterminez l’expression de la loi de vitesse globale.

Solution

Pour la réaction globale, il suffit d’additionner les trois étapes, d’annuler les intermédiaires et de combiner les formules similaires:

2NO₂Cl (g) → 2NO₂ (g) + Cl₂ (g)

Ensuite, écrivez l’expression de la loi de vitesse pour chaque réaction élémentaire. Rappelez-vous que pour les réactions élémentaires qui font partie d’un mécanisme, l’expression de la loi de vitesse peut être dérivée directement de la stœchiométrie:

k₁[NO₂Cl]₂ = k_-1 [ClO₂][N₂O][ClO]

k₂[N₂O][ClO₂] = k_-2[NO₂][NOCl]

Vitesse = k₃ [NOCl][ClO]

La troisième étape, qui est l’étape lente, est l’étape déterminant la vitesse. Par conséquent, l’expression de la loi de vitesse globale pourrait s’écrire Vitesse = k₃ [NOCl][ClO]. Cependant, le NOCl et le ClO sont tous deux des intermédiaires. Des expressions algébriques doivent être utilisées pour représenter [NOCl] et [ClO] de manière à ce qu’aucun intermédiaire ne subsiste dans l’expression de la loi de vitesse globale.

En utilisant la réaction élémentaire 1,

[ClO] = k₁[NO₂Cl]² k_-1[ClO₂][N₂O]

Utilisation de la réaction élémentaire 2,

[NOCl] = k₂[N₂O][ClO₂]k_-2[NO₂]

Substituez maintenant ces expressions algébriques dans l’expression de la loi de vitesse global et simplifiez:

vitesse = k₃ (k₂[N₂O][ClO₂]k_-2[NO₂]) (k₁[NO₂Cl]²k_-1[ClO₂][N₂O])

vitesse = k₁k₂k₃[NO₂Cl]2k = 2k_-1[NO₂]

Remarquez que cette loi de vitesse présente une dépendance inverse de la concentration de l’un des produits, ce qui est cohérent avec la présence d’une étape d’équilibre dans le mécanisme de réaction.

Vérifiez votre apprentissage 7.7.1 (en utilisant l’approximation de l’état stationnaire) – Détermination de l’expression de la loi de vitesse globale pour un mécanisme de réaction à plusieurs étapes

Le chlore atomique dans l’atmosphère réagit avec l’ozone dans la paire de réactions élémentaires suivante:

Cl + O₃ (g)  →  ClO (g) + O₂ (g) (constante de vitesse k₁)

ClO (g) + O  →  Cl (g) + O₂ (g) (constante de vitesse k₂)

Déterminez la réaction globale, écrivez l’expression de la loi de vitesse pour chaque réaction élémentaire, identifiez tout intermédiaire et déterminez l’expression de la loi de vitesse globale.

Réponse

réaction globale : O₃ (g) + O → 2O₂ (g)

vitesse₁ = k₁[O₃][Cl]; vitesse₂ = k₂[ClO][O]

intermédiaire: ClO (g)

vitesse globale = k₂k₁[O₃][Cl][O]

Questions

★★ Questions

Dans un mécanisme alternatif pour la réaction de NO₂ avec CO, N₂O₄ apparaît comme un intermédiaire. Écrivez la loi de vitesse pour chaque réaction élémentaire. Ce mécanisme est-il cohérent avec la loi de vitesse déterminée expérimentalement (vitesse = k[NO₂]₂) ?

Le monochlorure d’iode (ICl) réagit avec H₂ comme suit. 2ICl (l) + H₂ (g)  →  2HCl (g) + I₂ (s). La loi de vitesse déterminée expérimentalement est vitesse = k[ICl][H₂]. Écrivez un mécanisme en deux étapes pour cette réaction en utilisant uniquement des réactions élémentaires bimoléculaires et montrez qu’il est cohérent avec la loi de vitesse expérimentale. (Indice: HI est un intermédiaire).

Supposez que la réaction entre NO et H₂ se produit par un processus en trois étapes. Écrivez la loi de vitesse pour chaque réaction élémentaire, écrivez l’équation chimique équilibrée pour la réaction globale, et identifiez l’étape déterminant la vitesse. La loi de vitesse pour l’étape déterminant la vitesse est-elle cohérente avec la loi de vitesse dérivée expérimentalement pour la réaction globale: vitesse = k[NO]²[H₂]?

Réponses

La loi de vitesse pour l’étape 1 est: vitesse = k₁[NO₂]²; pour l’étape 2, c’est: vitesse = k₂[N₂O₄][CO]. Si l’étape 1 est lente (et donc l’étape déterminant la vitesse), alors la loi de vitesse globale de la réaction sera la même: vitesse = k₁[NO₂]². C’est la même que la loi de vitesse déterminée expérimentalement. Par conséquent, ce mécanisme, avec N₂O₄ comme intermédiaire, et celui décrit précédemment, avec NO₃ comme intermédiaire, sont cinétiquement indiscernables. Dans ce cas, d’autres expériences sont nécessaires pour les distinguer. Par exemple, le chercheur pourrait essayer de détecter directement les intermédiaires proposés, NO₃ et N₂O₄.

Ce mécanisme est compatible avec la loi de vitesse expérimentale si la première étape est l’étape déterminant la vitesse.

Étape déterminant la vitesse de formation = #2. Oui, car la vitesse de formation de [N₂O₂] =k₁[NO]². En substituant k₁[NO]² à [N₂O₂] dans la loi de vitesse de l’étape 2, on obtient la loi de vitesse dérivée expérimentalement pour la réaction chimique globale, où k = k₁k₂.

•Étape 1 : vitesse = k₁[NO]2

•Étape 2 : vitesse = k₂[N₂O₂][H₂]

•Étape 3 : vitesse = k₂[N₂O₂][H₂]

La réaction globale est alors

2NO _(g) + 2H_{2 (g)} → N_{2 (g)} + 2H₂O _(g)