7.5 – Théorie des Collisions

Nous ne devrions pas être surpris que les atomes, les molécules ou les ions doivent entrer en collision avant de réagir. Les atomes doivent être proches les uns des autres pour former des liaisons chimiques. Cette simple prémisse est la base d’une théorie très puissante qui explique de nombreuses observations concernant la cinétique chimique, y compris les facteurs affectant les vitesses de réaction.

La théorie des collisions repose sur les postulats suivants:

1) La vitesse d’une réaction est proportionnelle au vitesse de collisions des réactifs:

2) Les espèces qui réagissent doivent entrer en collision dans une orientation qui permet le contact entre les atomes qui seront liés ensemble dans le produit.

3) La collision doit se produire avec une énergie suffisante pour permettre la pénétration mutuelle des couches de valence des espèces qui réagissent, afin que les électrons puissent se réarranger et former de nouvelles liaisons (et de nouvelles espèces chimiques).

Nous pouvons voir l’importance des deux facteurs physiques notés dans les postulats 2 et 3, l’orientation et l’énergie des collisions, lorsque nous considérons la réaction du monoxyde de carbone avec l’oxygène:

2CO (g) + O₂ (g) → 2CO₂ (g)

Le monoxyde de carbone est un polluant produit par la combustion de carburants hydrocarbonés. Pour réduire ce polluant, les automobiles sont équipées de convertisseurs catalytiques qui utilisent un catalyseur pour effectuer cette réaction. Le monoxyde de carbone est également une réaction secondaire de la combustion de la poudre à canon, qui se traduit par un éclair debouche de nombreuses armes à feu. Si le monoxyde de carbone et l’oxygène sont présents en quantité suffisante, la réaction est spontanée à température et pression élevées.

La première étape de la réaction en phase gazeuse entre le monoxyde de carbone et l’oxygène est une collision entre les deux molécules:

Bien qu’il existe de nombreuses orientations possibles des deux molécules l’une par rapport à l’autre, considérons les deux cas présentés à la Figure 7.5.1. Dans le premier cas, le côté oxygène de la molécule de monoxyde de carbone entre en collision avec la molécule d’oxygène. Dans le second cas, le côté carbone de la molécule de monoxyde de carbone entre en collision avec la molécule d’oxygène. Le second cas est nettement plus susceptible de résulter à la formation de dioxyde de carbone, dont l’atome de carbone central est lié à deux atomes d’oxygène (O=C=O). Il s’agit d’un exemple assez simple de l’importance de l’orientation de la collision pour la création du produit souhaité de la réaction.

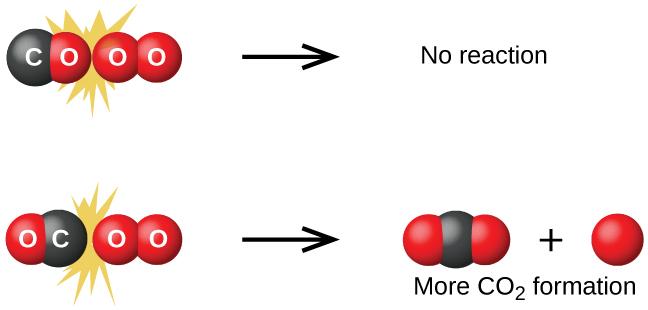
Figure 7.5.1. Elle illustre deux collisions qui pourraient avoir lieu entre des molécules de monoxyde de carbone et d’oxygène. L’orientation des molécules en collision détermine en partie si une réaction entre les deux molécules va se produire.

Si la collision a lieu avec l’orientation correcte, il n’y a toujours aucune garantie que la réaction se poursuivra pour former du dioxyde de carbone. Toute réaction nécessite une certaine quantité d’énergie d’activation pour se dérouler dans le sens direct, en produisant un complexe activé approprié en cours de route. Comme le montre la Figure 7.5.2., même une collision ayant la bonne orientation peut ne pas former le produit de la réaction. Dans l’étude des mécanismes réactionnels, chacun de ces trois arrangements d’atomes est appelé complexe activé proposé ou état de transition.

O = C •••O = O

O•••C•••O = O

O = C •••O•••O

Figure 7.5.2. États de transition possibles (complexes activés) pour le monoxyde de carbone réagissant avec l’oxygène pour former du dioxyde de carbone. Les lignes solides représentent des liaisons covalentes, tandis que les lignes en pointillés représentent des chevauchements d’orbitales instables qui peuvent, ou non, devenir des liaisons covalentes lors de la formation du produit. Dans les deux premiers exemples de cette figure, la double liaison O=O n’est pas touchée; par conséquent, le dioxyde de carbone ne peut pas se former. Le troisième état de transition proposé entraînera la formation de dioxyde de carbone si le troisième atome d’oxygène “supplémentaire” se sépare du reste de la molécule.

Dans la plupart des cas, il est impossible d’isoler ou d’identifier un état de transition ou un complexe activé. Dans la réaction entre le monoxyde de carbone et l’oxygène pour former du dioxyde de carbone, les complexes activés n’ont été observés par spectroscopie que dans des systèmes utilisant un catalyseur hétérogène. La réaction en phase gazeuse se produit trop rapidement pour isoler un tel composé chimique.

La théorie des collisions explique pourquoi la plupart des vitesses de réaction augmentent lorsque la concentration augmente. Avec l’augmentation de la concentration d’une substance en réaction, les chances de collisions entre les molécules augmentent car il y a plus de molécules par unité de volume. Plus de collisions signifie une vitesse de réaction plus rapide, à condition que l’énergie des collisions soit adéquate.

Énergie d‘activation et équation d’Arrhenius

L’énergie minimale nécessaire à la formation d’un produit lors d’une collision entre réactifs est appelée énergie d'activation (E_a). L’énergie cinétique des molécules réactives joue un rôle important dans une réaction car l’énergie nécessaire à la formation d’un produit est fournie par la collision d’une molécule réactive avec une autre molécule réactive. (Dans les réactions à un seul réactif, l’énergie d’activation peut être fournie par une collision de la molécule de réactif avec la paroi du récipient de réaction ou avec des molécules d’un contaminant inerte). Si l’énergie d’activation est beaucoup plus grande que l’énergie cinétique moyenne des molécules, la réaction se produira lentement: Seules quelques molécules se déplaçant rapidement auront suffisamment d’énergie pour réagir. Si l’énergie d’activation est beaucoup plus petite que l’énergie cinétique moyenne des molécules, la fraction de molécules possédant l’énergie cinétique nécessaire sera importante; la plupart des collisions entre molécules entraîneront une réaction, et la réaction se produira rapidement.

La Figure 7.5.3. montre les relations énergétiques pour la réaction générale d’une molécule de A avec une molécule de B pour former des molécules de C et D:

A + B  →  C + D

La figure montre que l’énergie de l’état de transition est supérieure à celle des réactifs A et B d’une quantité égale à E_a, l’énergie d’activation. Ainsi, la somme des énergies cinétiques de A et B doit être égale ou supérieure à E_a pour atteindre l’état de transition. Une fois l’état de transition atteint, et lorsque C et D commencent à se former, le système perd de l’énergie jusqu’à ce que son énergie totale soit inférieure à celle du mélange initial. Cette énergie perdue est transférée aux autres molécules, leur donnant suffisamment d’énergie pour atteindre l’état de transition. La réaction directe (celle entre les molécules A et B) a donc tendance à se produire facilement une fois que la réaction a commencé. Dans la Figure 7.5.3, ΔH représente la différence d’enthalpie entre les réactifs (A et B) et les produits (C et D). La somme de E_a et de ΔH représente l’énergie d’activation de la réaction inverse:

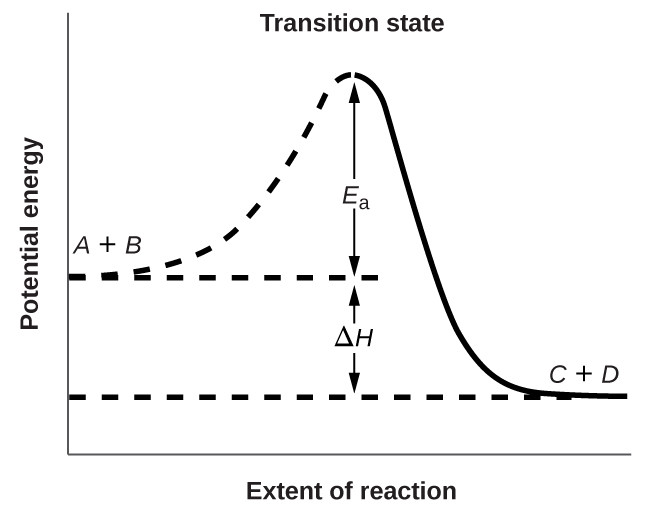
Figure 7.5.3. Ce graphique montre les relations d’énergie potentielle pour la réaction A+B⟶C+D. La partie en pointillés de la courbe représente l’énergie du système avec une molécule A et une molécule B présentes, et la ligne solide représente l’énergie du système avec une molécule C et une molécule D présentes. L’énergie d’activation pour la réaction directe est représentée par E_a. L’énergie d’activation de la réaction inverse est supérieure à celle de la réaction directe d’une quantité égale à ΔH. Le pic de la courbe est représenté l’état de transition.

Nous pouvons utiliser l'équation d'Arrhenius pour relier l’énergie d’activation et la constante de vitesse, k, d’une réaction donnée:

k=Ae^-EaIRT

Équation 7.5.1 Équation d’Arrhenius

Dans cette équation, R est la constante des gaz idéaux, qui a une valeur de 8,314 J/mol/K, T est la température sur l’échelle de Kelvin, E_a est l’énergie d’activation en joules par mole, e est la fonction exponentielle naturelle avec une valeur approximative de 2,7183, et A est une constante appelée facteur pré-exponentiel, qui est liée à la fréquence des collisions et à l’orientation des molécules en réaction.

Les deux postulats de la théorie de la collision des vitesses de réaction sont pris en compte dans l’équation d’Arrhenius. Le facteur pré-exponentiel A est lié à la vitesse à laquelle se produisent les collisions ayant la bonne orientation. Le terme exponentiel, e^–Ea/RT, est lié à la fraction des collisions fournissant une énergie suffisante pour surmonter la barrière d’activation de la réaction.

À un extrême, le système ne contient pas assez d’énergie pour que les collisions permettent de surmonter la barrière d’activation. Dans ce cas, aucune réaction ne se produit. À l’autre extrême, le système contient tellement d’énergie que chaque collision avec la bonne orientation peut surmonter la barrière d’activation, ce qui entraîne la réaction. Dans ce cas, la réaction est presque instantanée.

L’équation d’Arrhenius décrit quantitativement une grande partie de ce que nous avons déjà discuté sur les vitesses de réaction. Pour deux réactions à la même température, la réaction ayant l’énergie d’activation la plus élevée a la constante de vitesse la plus faible et la vitesse la plus lente. La plus grande valeur de E_a entraîne une plus petite valeur de e^–Ea/RT, reflétant la plus petite fraction de molécules ayant suffisamment d’énergie pour réagir. Alternativement, la réaction avec la plus petite valeur de E_a a une plus grande fraction de molécules avec assez d’énergie pour réagir. Cela se traduira par une valeur plus élevée de e^–Ea/RT, une constante de vitesse plus élevée et une vitesse plus rapide de la réaction. Une augmentation de la température a le même effet qu’une diminution de l’énergie d’activation. Une fraction plus importante de molécules possède l’énergie nécessaire pour réagir (Figure 7.5.4.), comme l’indique une augmentation de la valeur de e^–Ea/RT. La constante de vitesse est également directement proportionnelle au facteur pré-exponentiel, A. Ainsi, un changement des conditions ou des réactifs qui augmente le nombre de collisions avec une orientation favorable à la réaction entraîne une augmentation de A et, par conséquent, une augmentation de k.

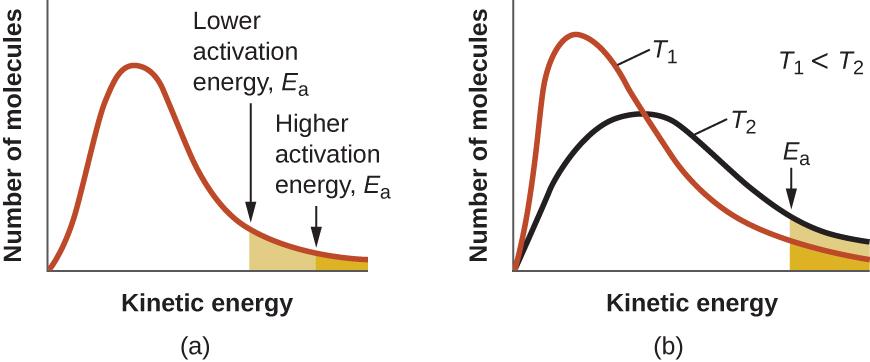
Figure 7.5.4. (a) Lorsque l’énergie d’activation d’une réaction diminue, le nombre de molécules ayant au moins cette énergie augmente, comme le montrent les zones ombrées. (b) À une température plus élevée, T₂, davantage de molécules ont une énergie cinétique supérieure à E_a, comme le montre la zone ombrée en jaune.

Une approche pratique pour déterminer E_a pour une réaction implique la mesure de k à différentes températures et l’utilisation d’une version alternative de l’équation d’Arrhenius qui prend la forme d’une équation linéaire:

Ainsi, un graphique de ln k en fonction de 1T donne une ligne droite avec la pente –E_aR à partir de laquelle on peut déterminer E_a. L’ordonnée à l’origine donne la valeur de ln A.

Exemple 7.5.1 – Détermination de E_a

La variation de la constante de vitesse avec la température pour la décomposition de HI (g) to H₂ (g) and I₂ (g) est donnée ici. Quelle est l’énergie d’activation de cette réaction?

2HI (g)  →  H₂ (g) + I₂ (g)

Solution

Les valeurs de 1T et ln k sont:

La Figure 7.5.5. est un graphique de ln k en fonction de 1T

Pour déterminer la pente de la droite, nous avons besoin de deux valeurs de ln k, qui sont déterminées à partir de la droite à deux valeurs de 1T

(il est préférable d’en avoir une près de chaque extrémité de la ligne). Par exemple, la valeur de ln k déterminée à partir de la droite lorsque 1T = 1,25 × 10^-3 est -2,593; la valeur lorsque 1T = 1,78 × 10^-3 est de -14,447.

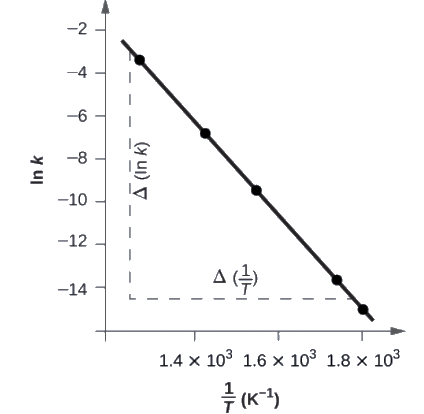
Figure 7.5.5. Ce graphique montre la relation linéaire entre ln k et 1T pour la réaction 2HI⟶H₂+I₂ selon l’équation d’Arrhenius.

La pente de cette droite est donnée par l’expression suivante:

Pente = Δ(lnk)Δ(1T) = (-14.447) – (-2.593)(1.78 x 10^-3K^-1) = (-11.854)(0.53 x 10^-3K^-1)) = 2.2 x 10⁴ K = -E_aR

Ainsi:

Dans de nombreuses situations, il est possible d’obtenir une estimation raisonnable de l’énergie d’activation sans passer par le processus complet de construction du diagramme d’Arrhenius. L’équation d’Arrhenius:

ln k = (-E_aR)(1T) + ln A

peut être réarrangé comme indiqué pour donner:

Cette équation peut être réarrangée pour donner un calcul en une étape permettant d’obtenir une estimation de l’énergie d’activation:

E_a = -R (lnk₂ – lnk₁ (1T₂ – 1T₁))

En utilisant les données expérimentales présentées ici, nous pouvons simplement sélectionner deux entrées de données. Pour cet exemple, nous sélectionnons la première entrée et la dernière entrée:

Après avoir calculé 1T et ln k, nous pouvons les substituer dans l’équation:

E_a = -8.314 Jmol^-1K^-1 (-3.231 – (-14.860) 1.28 × 10^-3K^-1 -1.80 × 10^-3K^-1) and the result is E_a = 185,900 J/mol.

Cette méthode est très efficace, surtout lorsqu’un nombre limité de constantes de vitesse dépendant de la température est disponible pour la réaction d’intérêt.

Vérifiez votre apprentissage 7.5.2 – Détermination de E_a

La constante de vitesse pour la vitesse de décomposition de N₂O₅ en NO et O₂ en phase gazeuse est de 1,66 L/mol/s à 650 K et de 7,39 L/mol/s à 700 K:

2 N₂O₅ (g)  →  4NO (g) + 3O₂ (g)

En supposant que la cinétique de cette réaction est conforme à l’équation d’Arrhenius, calculez l’énergie d’activation pour cette décomposition.

Réponse

113 000 J/mol

Questions

★ Questions

Les réactions chimiques se produisent lorsque les réactifs entrent en collision. Quels sont les deux facteurs qui peuvent empêcher une collision de produire une réaction chimique?

Qu’est-ce que l’énergie d’activation d’une réaction, et comment cette énergie est-elle liée au complexe activé de la réaction?

Lorsque chaque collision entre réactifs entraîne une réaction, qu’est-ce qui détermine la vitesse à laquelle la réaction se produit?

Décrire comment les méthodes graphiques peuvent être utilisées pour déterminer l’énergie d’activation d’une réaction à partir d’une série de données comprenant la vitesse de réaction à différentes températures.

Comment une augmentation de la température affecte-t-elle la vitesse de la réaction? Expliquez cet effet en termes de théorie de collision de la vitesse de réaction.

La vitesse d’une certaine réaction double pour chaque augmentation de 10 °C de la température.

Combien de fois la réaction se déroule-t-elle plus rapidement à 45 °C qu’à 25 °C?

Combien de fois la réaction se déroule-t-elle plus rapidement à 95 °C qu’à 25 °C?

★★ Questions

Un niveau élevé de l’enzyme phosphatase alcaline (ALP) dans le sérum est une indication d’une possible maladie du foie ou des os. La vitesse de sérum ALP est si faible qu’il est très difficile de le mesurer directement. Cependant, l’ALP catalyse un certain nombre de réactions, et sa concentration relative peut être déterminée en mesurant la vitesse de l’une de ces réactions dans des conditions contrôlées. L’une de ces réactions est la conversion du p-nitrophényl phosphate (PNPP) en ion p-nitrophénoxyde (PNP) et en ion phosphate. Le contrôle de la température pendant l’essai est très important; la vitesse de la réaction augmente de 1,47 fois si la température passe de 30 °C à 37 °C. Quelle est l’énergie d’activation (en kJ/mol) pour la conversion catalysée par l’ALP du PNPP en PNP et en phosphate?

L’iodure d’hydrogène, HI, se décompose en phase gazeuse pour produire de l’hydrogène, H₂, et de l’iode, I₂. La valeur de la constante de vitesse, k, pour cette réaction a été mesurée à plusieurs températures différentes et les données sont présentées ici. Quelle est la valeur de l’énergie d’activation (en kJ/mol) pour cette réaction?

Réponses

Les réactifs peuvent soit se déplacer trop lentement pour avoir suffisamment d’énergie cinétique pour dépasser l’énergie d’activation de la réaction, soit l’orientation des molécules au moment de leur collision peut empêcher la réaction de se produire.

L’énergie d’activation est la quantité minimale d’énergie nécessaire pour former le complexe activé dans une réaction. Elle est généralement exprimée comme l’énergie nécessaire pour former une mole de complexe activé.

Ordre de la réaction et concentration

Après avoir trouvé k à plusieurs températures différentes, un graphique de ln k en fonction de 1/T, donne une ligne droite avec la pente –E_a/R à partir de laquelle E_a peut être déterminée.

Lorsque la température augmente, la vitesse moyenne globale des particules augmente également. Par conséquent, l’énergie cinétique augmente, ce qui permet aux particules d’entrer en collision plus fréquemment. Avec plus de collisions, la vitesse de la réaction augmente également.

(a) 4 fois plus rapide (b) 128 fois plus rapide

43,0 kJ/mol

177 kJ/mol